Limites lio n 1 1 Conceito de Limite

Limites – lição nº 1 1

Conceito de Limite Círculos com área = A n = 4 lados área =a 4 n = 5 lados área =a 5 n = 6 lados área =a 6 n = 8 lados área =a 8 Aumentando o número de lados do polígono inscrito, a sua área aproxima-se da área do círculo sem NUNCA a igualar. Diz-se que o Limite da área do polígono de “n” lados, A n, quando “n” tende para Infinito é a área “A” do círculo. 2

A “ideia” do limite Começamos com um número “c” e todos os valores “x”, da função f(x), que sejam próximos de “c” mas diferentes deste. Sendo “L” um número real, diz-se que o limite de f(x), à medida que “x” tende para “c”, é L. Notar que f(x) ser ou não ser definida em “c” é irrelevante. Leituras possíveis sem preocupação de rigor - À medida que “x” se aproxima de “c”, f(x) aproxima-se de “L” - f(x) é tão próximo de “L” quanto “x” o é de “c” 3

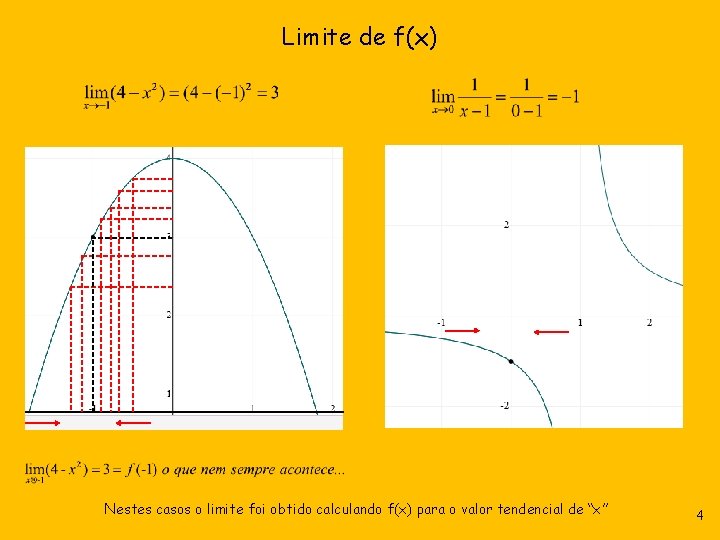
Limite de f(x) Nestes casos o limite foi obtido calculando f(x) para o valor tendencial de “x” 4

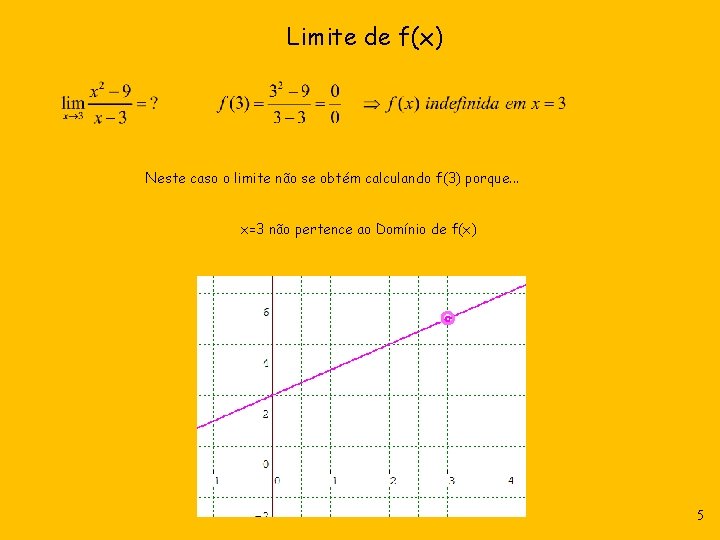
Limite de f(x) Neste caso o limite não se obtém calculando f(3) porque. . . x=3 não pertence ao Domínio de f(x) 5

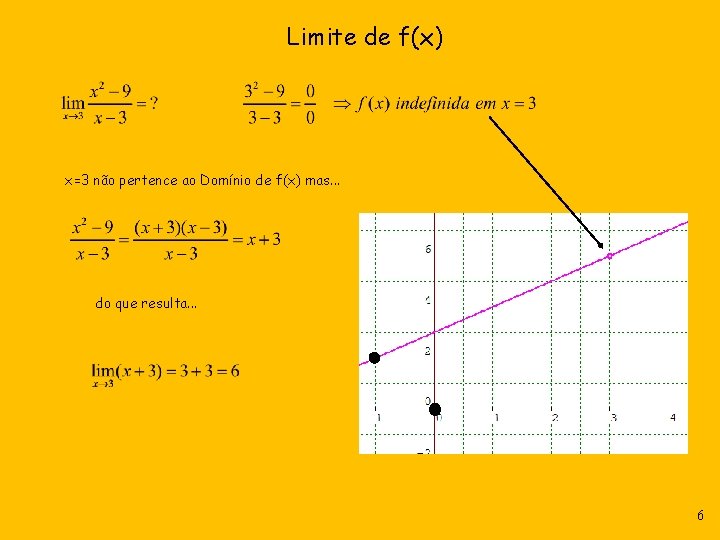
Limite de f(x) x=3 não pertence ao Domínio de f(x) mas. . . do que resulta. . . 6

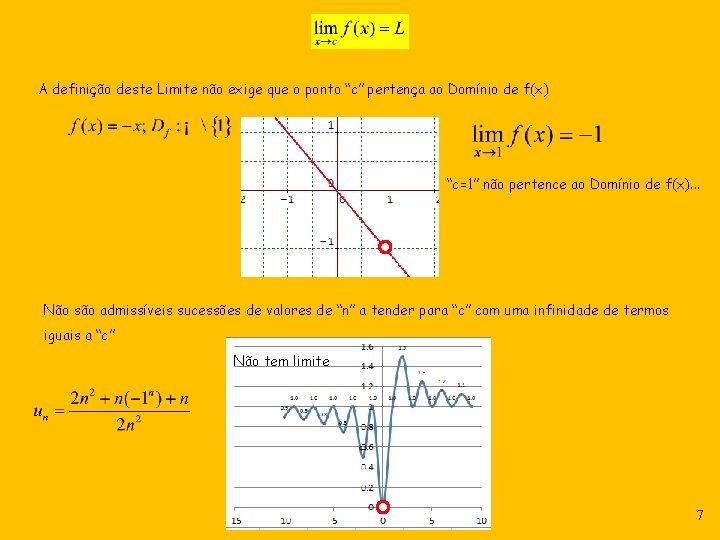
A definição deste Limite não exige que o ponto “c” pertença ao Domínio de f(x) “c=1” não pertence ao Domínio de f(x). . . Não são admissíveis sucessões de valores de “n” a tender para “c” com uma infinidade de termos iguais a “c” Não tem limite 7

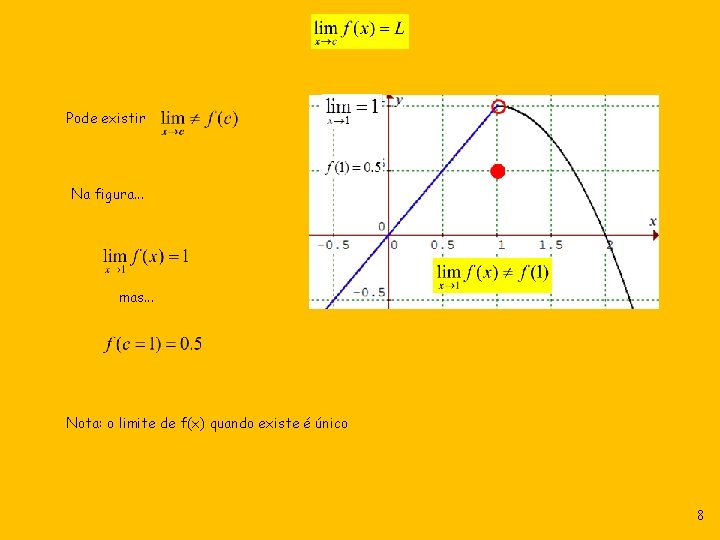
Pode existir Na figura. . . mas. . . Nota: o limite de f(x) quando existe é único 8

Ponto de Acumulação Ponto “ 0” não pertence ao conjunto “A”, mas. . . é um Ponto de Acumulação de “A” porque, na sua vizinhança, há pelo menos um elemento de “A” Ponto “ 3” pertence ao conjunto “A”, mas. . . não é Ponto de Acumulação de “A” porque, na sua vizinhança, não há pelo menos um elemento de “A” Resulta daqui que: Se o domínio de f(x) é o conjunto “A” 9

Limites Laterais O limite não pode ser obtido calculando f(1). . . mas observando o gráfico. . . para x+ = 2, 1. 99, . . . , 1. 02, . . . , 1. 001 (aproximação pela direita) e. . . para x- = 0, 0. 8, . . . , 0. 99 (aproximação pela esquerda) O limite existe, sendo igual a 1 10

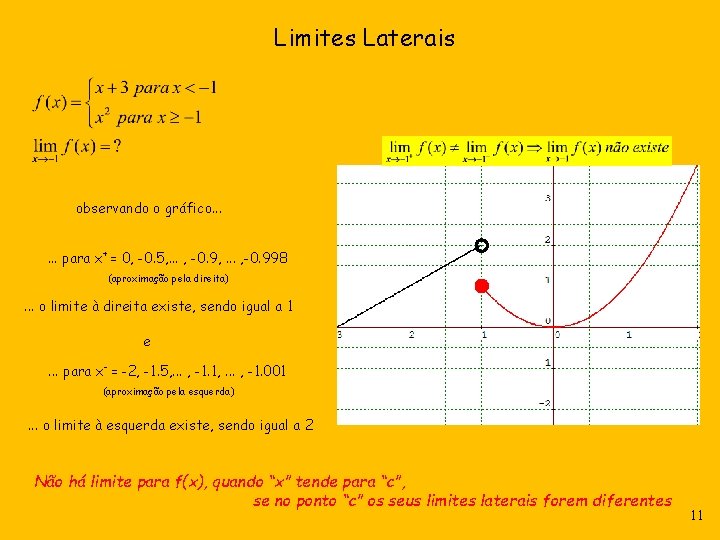
Limites Laterais observando o gráfico. . . para x+ = 0, -0. 5, . . . , -0. 998 (aproximação pela direita) . . . o limite à direita existe, sendo igual a 1 e. . . para x- = -2, -1. 5, . . . , -1. 1, . . . , -1. 001 (aproximação pela esquerda) . . . o limite à esquerda existe, sendo igual a 2 Não há limite para f(x), quando “x” tende para “c”, se no ponto “c” os seus limites laterais forem diferentes 11

Limite segundo Heines Diz-se que o limite de f(x) é “b” quando “x” tende para “a”. . . se a toda a sucessão (xn) que tende para valores de “a”, por valores do domínio de f(x), excepto “a”. . . corresponde uma sucessão (f(xn )) que tende para “b” Não há limite de f(x) quando “x” tende para “a”. . . quando o limite da sucessão (f(xn)) for Infinito (+ ou -) 12

Limite segundo Heines Consideramos uma sucessão (xn) de valores reais do domínio de f(x) ( excepto 2) , que tende para 2. . . do que resulta un = xn - 2 tender para zero. Recorrendo à sucessão vn=f(xn) - 5 temos: Dado que un = xn - 2 tender para zero então: 13

Para meditar. . . não faz sentido porque. . . obrigando a concluir que “infinito” não tem tradução numérica. . . pelo que. . . 14

Infinito - Indeterminações 15

Álgebra dos limites 1. Função constante O limite de uma função constante é a própria constante 2. Função identidade O limite de uma função identidade é o valor para que tende a variável independente 17

Álgebra dos limites 3. Limite da soma de funções O limite de uma soma de funções é igual à soma dos limites das parcelas. . . se e só se. . . estes limites existem e não são Infinitos de sinal diferente 18

Álgebra dos limites 4. Limite da diferença de funções O limite de uma diferença de funções é igual à diferença dos respectivos limites. . . se e só se. . . estes limites existem e não são Infinitos do mesmo sinal 19

Álgebra dos limites 5. Limite do produto de funções O limite do produto de funções é igual ao produto dos limites dos factores. . . se e só se. . . estes limites existem sem que um deles seja infinito e o outro nulo 20

Álgebra dos limites 6. Limite do quociente de funções O limite dum quociente de funções é igual ao quociente do limite do dividendo pelo limite do divisor. . . se e só se. . . estes limites existem e não são ambos nulos ou ambos infinitos 21

Álgebra dos limites 7. Limite da Raiz O limite da raiz de uma função é igual à raiz do limite da mesma, caso exista 22

EXEMPLOS 23

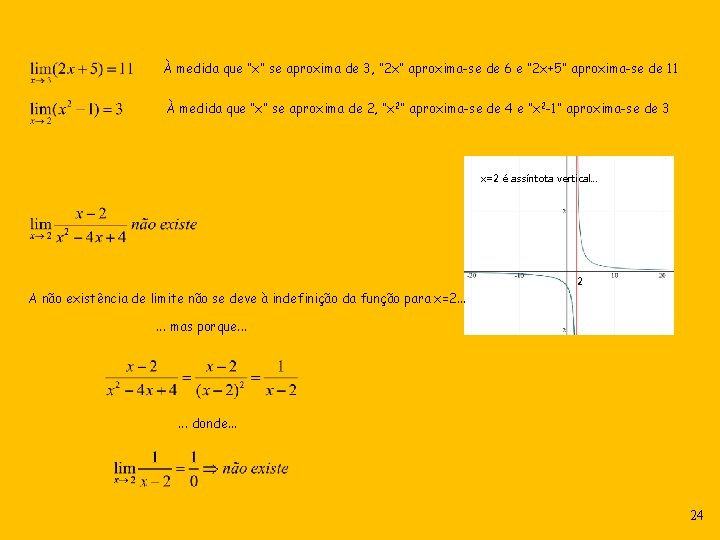
À medida que “x” se aproxima de 3, “ 2 x” aproxima-se de 6 e “ 2 x+5” aproxima-se de 11 À medida que “x” se aproxima de 2, “x 2” aproxima-se de 4 e “x 2 -1” aproxima-se de 3 x=2 é assíntota vertical. . . 2 A não existência de limite não se deve à indefinição da função para x=2. . . mas porque. . . donde. . . 24

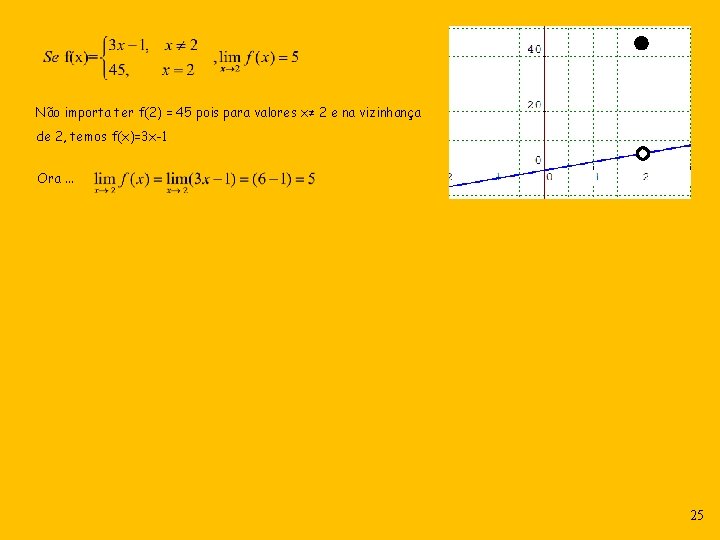
Não importa ter f(2) = 45 pois para valores x≠ 2 e na vizinhança de 2, temos f(x)=3 x-1 Ora. . . 25

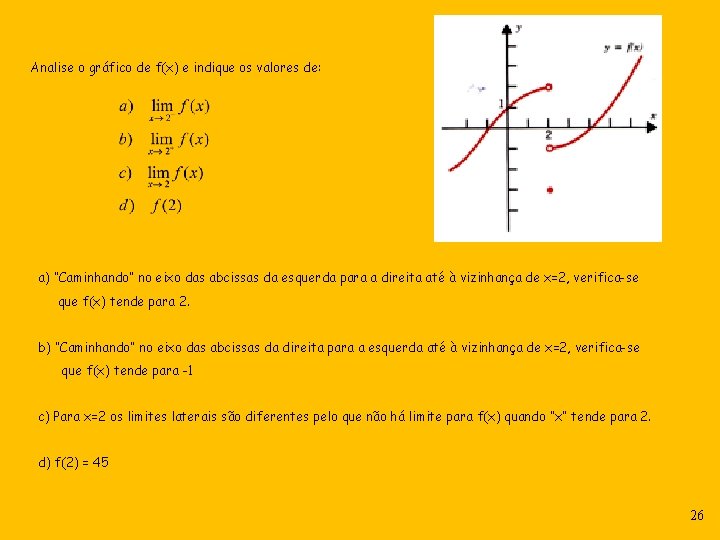
Analise o gráfico de f(x) e indique os valores de: a) “Caminhando” no eixo das abcissas da esquerda para a direita até à vizinhança de x=2, verifica-se que f(x) tende para 2. b) “Caminhando” no eixo das abcissas da direita para a esquerda até à vizinhança de x=2, verifica-se que f(x) tende para -1 c) Para x=2 os limites laterais são diferentes pelo que não há limite para f(x) quando “x” tende para 2. d) f(2) = 45 26

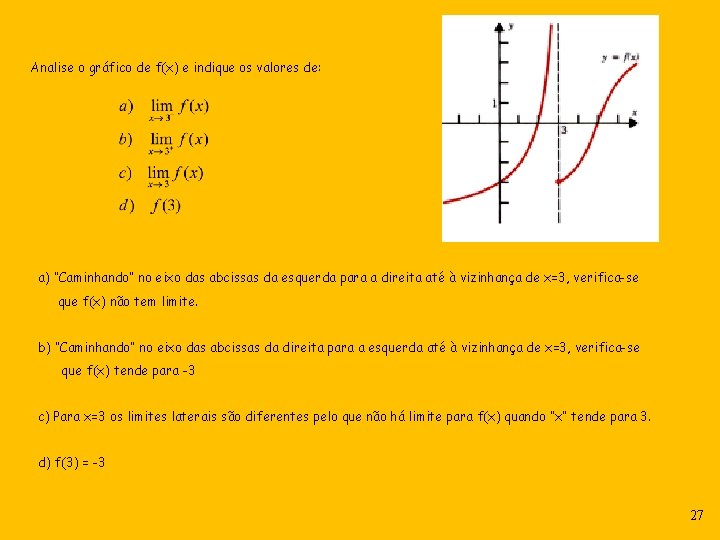
Analise o gráfico de f(x) e indique os valores de: a) “Caminhando” no eixo das abcissas da esquerda para a direita até à vizinhança de x=3, verifica-se que f(x) não tem limite. b) “Caminhando” no eixo das abcissas da direita para a esquerda até à vizinhança de x=3, verifica-se que f(x) tende para -3 c) Para x=3 os limites laterais são diferentes pelo que não há limite para f(x) quando “x” tende para 3. d) f(3) = -3 27

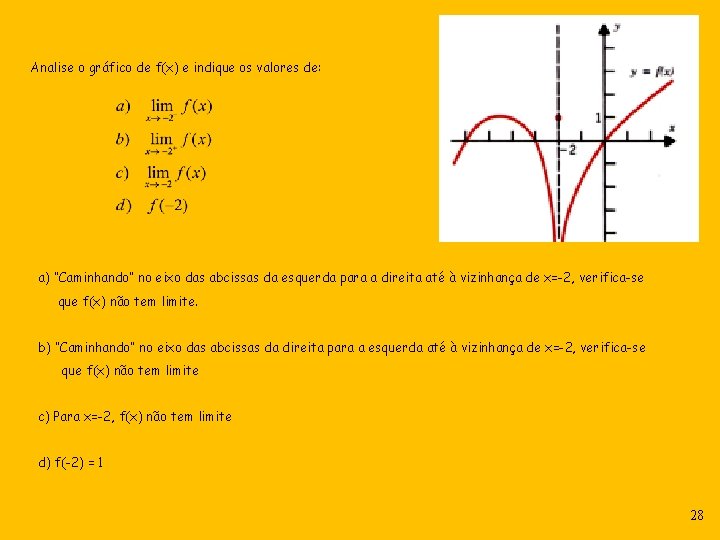
Analise o gráfico de f(x) e indique os valores de: a) “Caminhando” no eixo das abcissas da esquerda para a direita até à vizinhança de x=-2, verifica-se que f(x) não tem limite. b) “Caminhando” no eixo das abcissas da direita para a esquerda até à vizinhança de x=-2, verifica-se que f(x) não tem limite c) Para x=-2, f(x) não tem limite d) f(-2) = 1 28

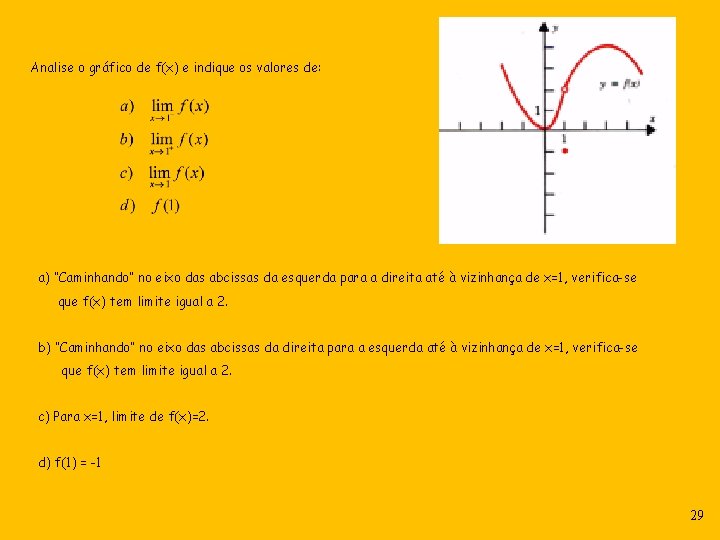
Analise o gráfico de f(x) e indique os valores de: a) “Caminhando” no eixo das abcissas da esquerda para a direita até à vizinhança de x=1, verifica-se que f(x) tem limite igual a 2. b) “Caminhando” no eixo das abcissas da direita para a esquerda até à vizinhança de x=1, verifica-se que f(x) tem limite igual a 2. c) Para x=1, limite de f(x)=2. d) f(1) = -1 29

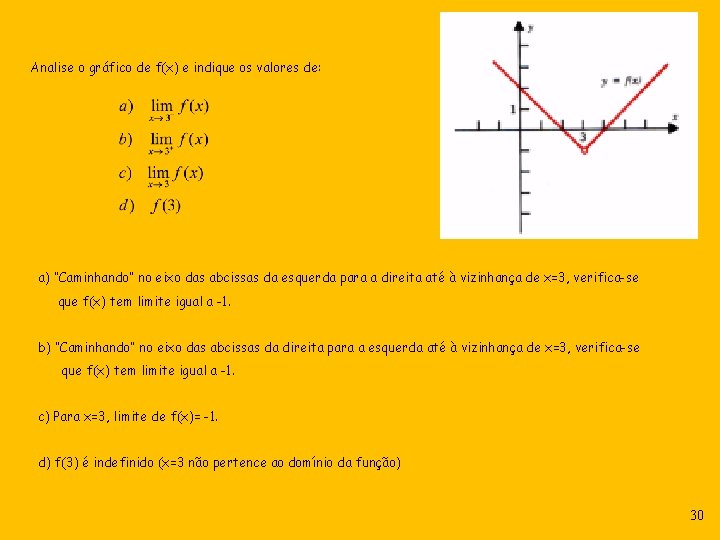
Analise o gráfico de f(x) e indique os valores de: a) “Caminhando” no eixo das abcissas da esquerda para a direita até à vizinhança de x=3, verifica-se que f(x) tem limite igual a -1. b) “Caminhando” no eixo das abcissas da direita para a esquerda até à vizinhança de x=3, verifica-se que f(x) tem limite igual a -1. c) Para x=3, limite de f(x)= -1. d) f(3) é indefinido (x=3 não pertence ao domínio da função) 30

Analise o gráfico de f(x) e indique os valores de: a) “Caminhando” no eixo das abcissas da esquerda para a direita até à vizinhança de x=2, verifica-se que f(x) tem limite igual a 0. b) “Caminhando” no eixo das abcissas da direita para a esquerda até à vizinhança de x=2, verifica-se que f(x) tem limite igual a 0. c) Para x=2, limite de f(x)= 0. d) f(2) = 0 31

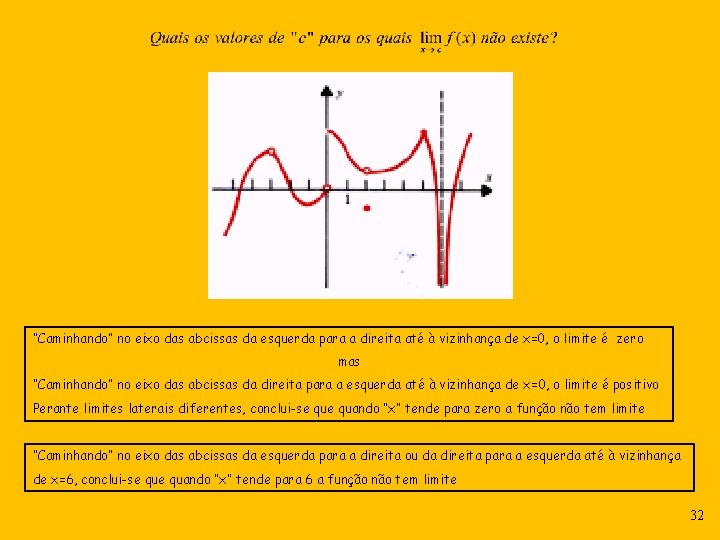
“Caminhando” no eixo das abcissas da esquerda para a direita até à vizinhança de x=0, o limite é zero mas “Caminhando” no eixo das abcissas da direita para a esquerda até à vizinhança de x=0, o limite é positivo Perante limites laterais diferentes, conclui-se quando “x” tende para zero a função não tem limite “Caminhando” no eixo das abcissas da esquerda para a direita ou da direita para a esquerda até à vizinhança de x=6, conclui-se quando “x” tende para 6 a função não tem limite 32

33