comandos TGH PRESENTA LIMITE Temas Limites Laterales Limites

comandos TGH PRESENTA LIMITE

Temas Limites Laterales Limites Infinitos Limites Para x Limites Infinitos para x

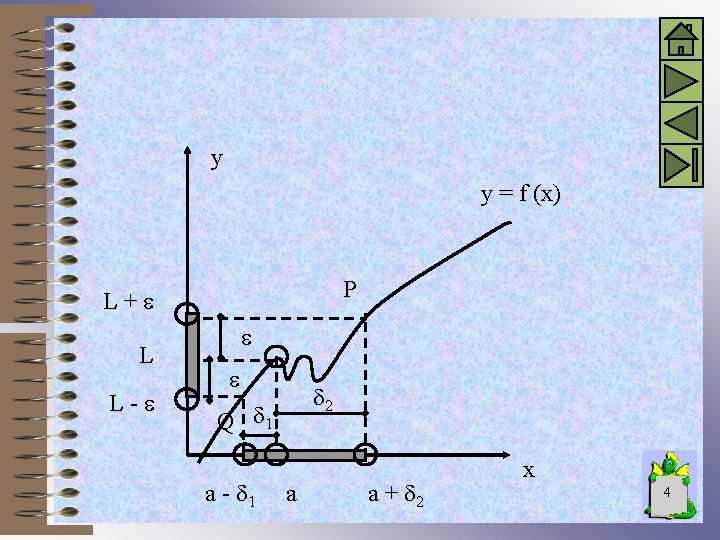
Límite Sea la función y = f(x) cuyo gráfico es el de la figura y deseamos determinar para que valores de x los valores de la función distan de L menos que una cantidad > 0 y arbitrariamente pequeña O sea para que valores entre L - y L + excluido el L - y L + y probablemente el L. En otras palabras deseamos saber para que valores de la x, la distancia entre la “y” y el valor L es < f(x) – L < [1] 3

y y = f (x) P L+ L L- 2 Q 1 a - 1 a a + 2 x 4

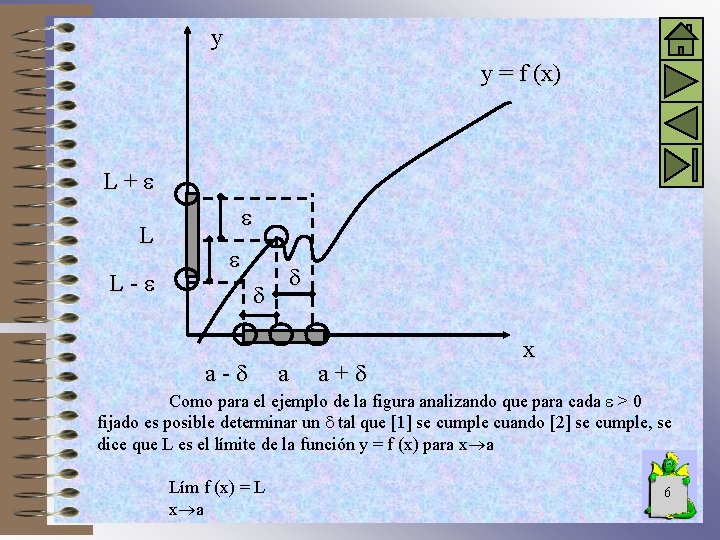
Para determinar esos valores gráficamente por L + sobre el eje y se traza una paralela al eje x hasta cortar al gráfico de la función en el punto P y por este punto una vertical. De igual modo se procede en L - y obtenemos el intervalo marcado en la figura en donde se cumple la condición [1]. Deseamos ahora determinar un entorno reducido del punto “a” para el cual sea válida [1]. En este caso hacemos = 1 0 < x - a < [2] Para determinarlo tomo por ejemplo desde x = a para la derecha y la izquierda un valor = 1 tengo un entorno reducido del punto x = a donde se cumple [1]. 5

y y = f (x) L+ L L- a- a a+ x Como para el ejemplo de la figura analizando que para cada > 0 fijado es posible determinar un tal que [1] se cumple cuando [2] se cumple, se dice que L es el límite de la función y = f (x) para x a Lím f (x) = L x a 6

Definición Supongamos tener una función y = f (x) definido en un entorno de un punto de abscisa x = a (excluido el punto a). Diremos que esa función tiene un límite L para x a y se escribe Lím f (x) = L x a Si para cada número > 0 arbitrariamente pequeño es posible determinar un > 0 tal que f(x) – L < para todos los x tales que 0 < x a < 7

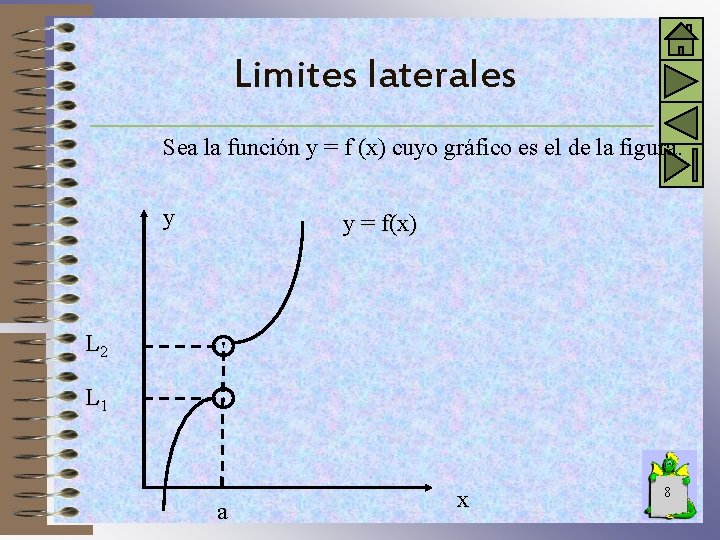
Limites laterales Sea la función y = f (x) cuyo gráfico es el de la figura. y y = f(x) L 2 L 1 a x 8

Observamos que cuando x se aproxima a “a” por la izquierda los valores de la función se aproximan a L 1. Decimos entonces que L 1 es el límite de f(x) para “x” tendiendo a “a” por la izquierda Lím f (x) = L 1 x a. En lenguaje matemático esto significa que para cada > 0 arbitrariamente pequeño es posible determinar un número > 0 tal que f (x) – L 1 < para todos los x tales que a - < x < a 9

Igualmente la figura nos muestra que cuando x se aproxima a “a” por la derecha los valores de la función se aproximan a L 2. Decimos entonces que L 2 es el límite de f(x) para x tendiendo a “a” por la derecha Lím f(x) = L 2 x a+ En lenguaje matemático esto significa que para cada > 0 arbitrariamente pequeño es posible determinar un número > 0 tal que f (x) – L 2 < para todos los x tales que a < x < a + 10

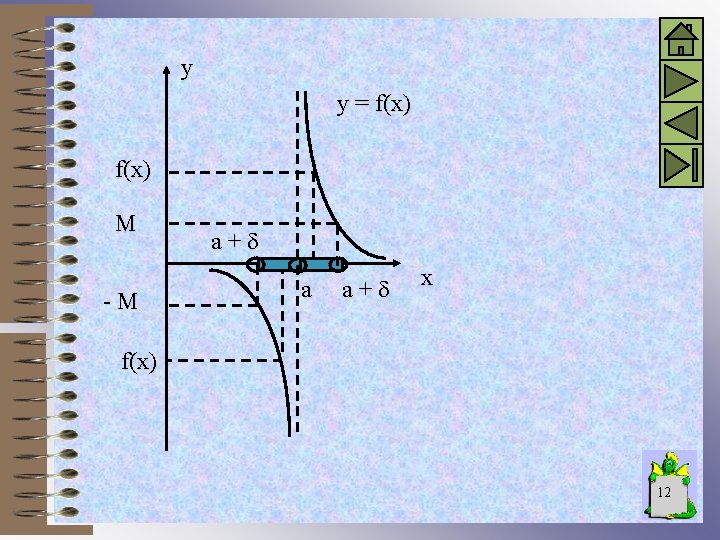
Límites infinitos Supongamos tener la función f (x) cuyo gráfico es el de la figura. Observamos que cuando x se aproxima a “a” por la derecha los valores de la función aumentan indefinidamente. Decimos entonces que es el límite de f(x) para x tendiendo a “a” por la derecha. Lím f (x) = + x a+ En lenguaje matemático esto significa que para cada M > 0 arbitrariamente grande es posible determinar un número > 0 tal que f(x) > M para todos los x tales que a < x < a + . 11

y y = f(x) M -M a+ a a+ x f(x) 12

Igualmente observamos que cuando x se aproxima a “a” por la izquierda los valores de la función disminuyen indefinidamente. Decimos entonces que - es el límite de f(x) para x tendiendo a “a” por la izquierda. Lím f(x) = - x a. En lenguaje matemático esto significa que para cada M > 0 arbitrariamente grande es posible determinar un número > 0 tal que f (x) < - M para todos los x tales que a - < x < a. 13

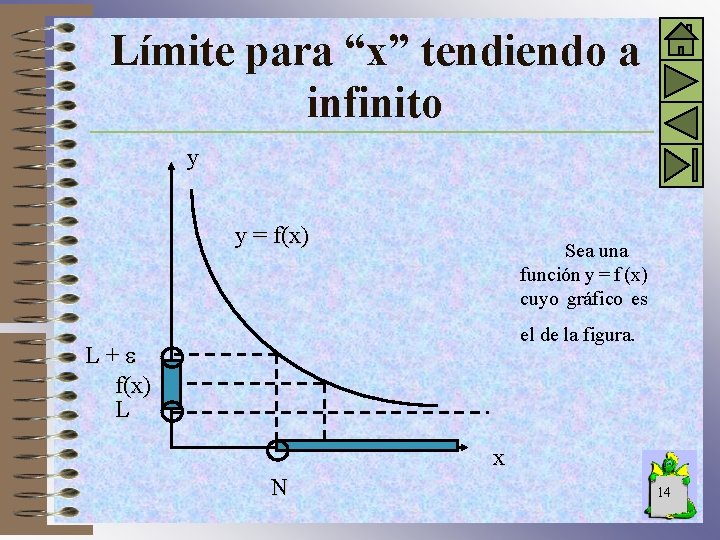
Límite para “x” tendiendo a infinito y y = f(x) Sea una función y = f (x) cuyo gráfico es el de la figura. L+ f(x) L x N 14

Observamos que cuando los valores positivos de x crecen indefinidamente, los valores de la función se aproximan a L. Decimos entonces que L es el límite de f (x) para x tendiendo , o sea: Lím f (x) = L x En lenguaje matemático esto significa que para cada > 0 arbitrariamente pequeño es posible determinar un número N > 0 tal que f(x) – L < para todos los x tales que N > x. 15

Límites infinitos para x tendiendo a infinito Sea una función y = f (x) cuyo gráfico es el de la figura. y y = f(x) M N x x 16

Observamos que cuando los valores positivos de x crecen indefinidamente, los valores positivos de la función también crecen indefinidamente L. Decimos entonces que es el límite de f(x) para x tendiendo , o sea: Lím f (x) = x En lenguaje matemático esto significa que para cada M > 0 arbitrariamente grande es posible determinar un número N > 0 tal que f (x) > M para todos los x tales que N > x. 17