Lesson Menu FiveMinute Check over Lesson 5 1

Lesson Menu Five-Minute Check (over Lesson 5– 1) Mathematical Practices Then/Now New Vocabulary Theorem 5. 7: Centroid Theorem Example 1: Use the Centroid Theorem Example 2: Use the Centroid Theorem Example 3: Real-World Example: Find the Centroid on a Coordinate Plane Key Concept: Orthocenter Example 4: Find the Orthocenter on a Coordinate Plane Concept Summary: Special Segments and Points in Triangles

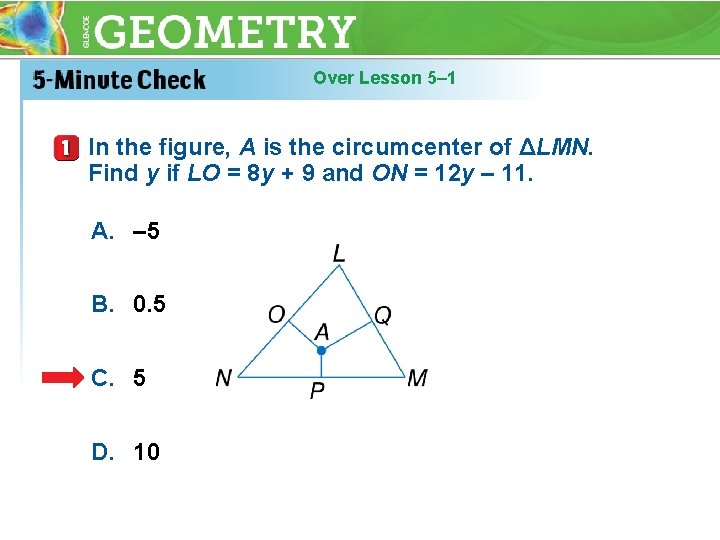
Over Lesson 5– 1 In the figure, A is the circumcenter of ΔLMN. Find y if LO = 8 y + 9 and ON = 12 y – 11. A. – 5 B. 0. 5 C. 5 D. 10

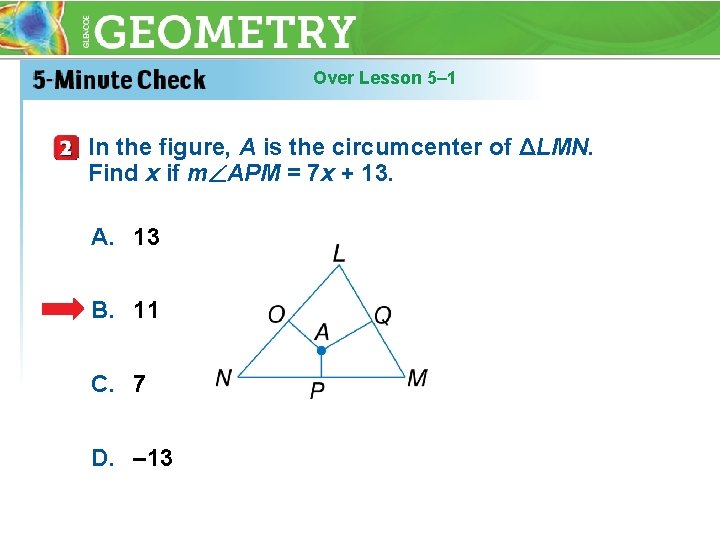
Over Lesson 5– 1 In the figure, A is the circumcenter of ΔLMN. Find x if m APM = 7 x + 13. A. 13 B. 11 C. 7 D. – 13

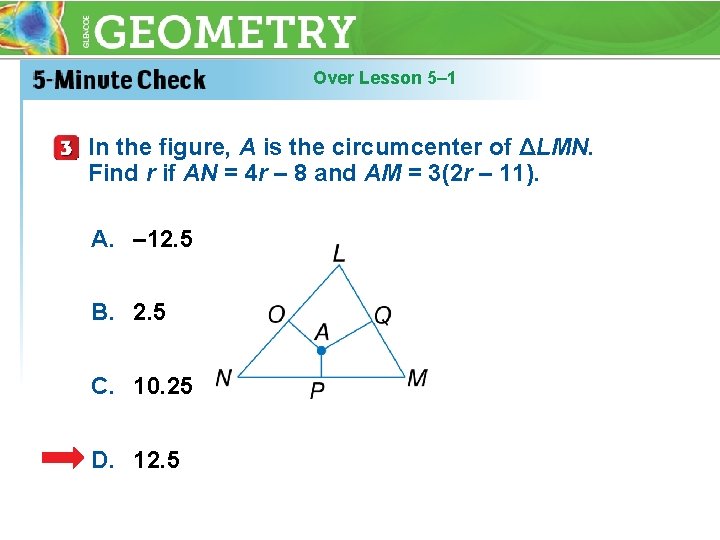
Over Lesson 5– 1 In the figure, A is the circumcenter of ΔLMN. Find r if AN = 4 r – 8 and AM = 3(2 r – 11). A. – 12. 5 B. 2. 5 C. 10. 25 D. 12. 5

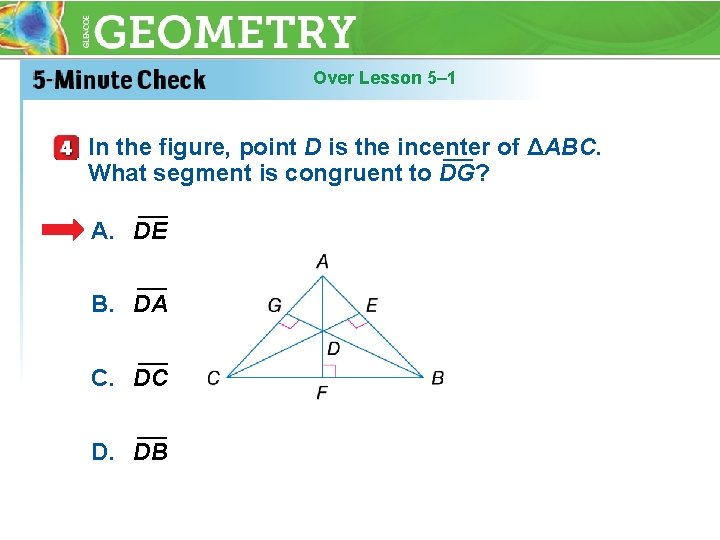
Over Lesson 5– 1 In the figure, point D is the incenter ___ of ΔABC. What segment is congruent to DG? ___ A. DE ___ B. DA ___ C. DC ___ D. DB

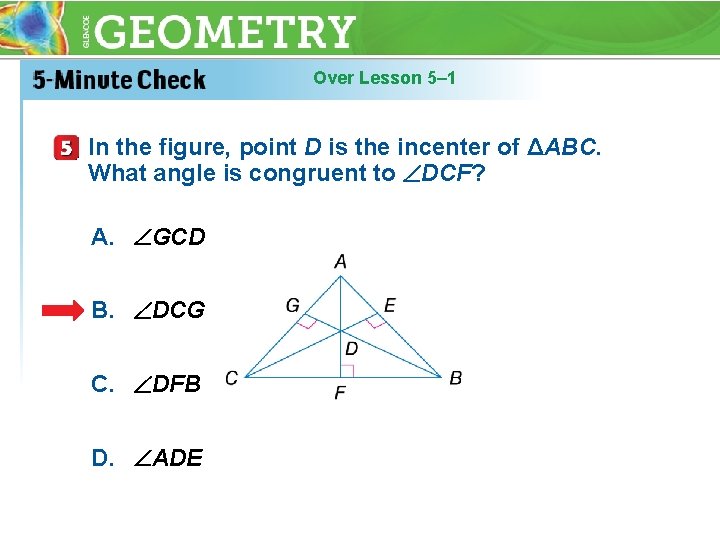
Over Lesson 5– 1 In the figure, point D is the incenter of ΔABC. What angle is congruent to DCF? A. GCD B. DCG C. DFB D. ADE

Over Lesson 5– 1 Which of the following statements about the circumcenter of a triangle is false? A. It is equidistant from the sides of the triangle. B. It can be located outside of the triangle. C. It is the point where the perpendicular bisectors intersect. D. It is the center of the circumscribed circle.

Mathematical Practices 6 Attend to precision. 3 Construct viable arguments and critique the reasoning of others. Content Standards G. CO. 10 Prove theorems about triangles. G. MG. 3 Apply geometric methods to solve problems (e. g. , designing an object or structure to satisfy physical constraints or minimize cost; working with typographic grid systems based on ratios).

You identified and used perpendicular and angle bisectors in triangles. • Identify and use medians in triangles. • Identify and use altitudes in triangles.

• median • centroid • altitude • orthocenter

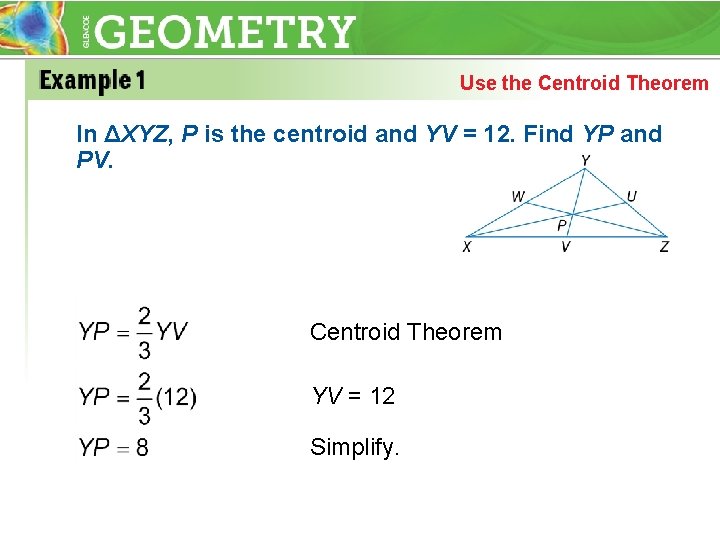
Use the Centroid Theorem In ΔXYZ, P is the centroid and YV = 12. Find YP and PV. Centroid Theorem YV = 12 Simplify.

Use the Centroid Theorem YP + PV = YV 8 + PV = 12 PV = 4 Answer: YP = 8; PV = 4 Segment Addition YP = 8 Subtract 8 from each side.

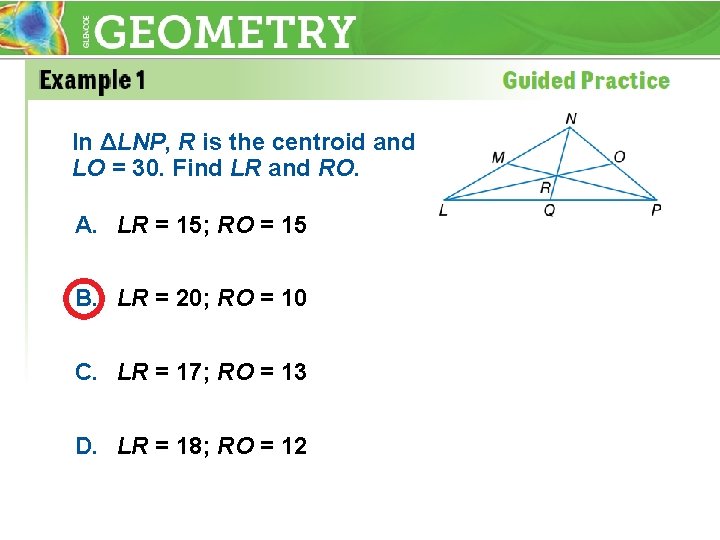
In ΔLNP, R is the centroid and LO = 30. Find LR and RO. A. LR = 15; RO = 15 B. LR = 20; RO = 10 C. LR = 17; RO = 13 D. LR = 18; RO = 12

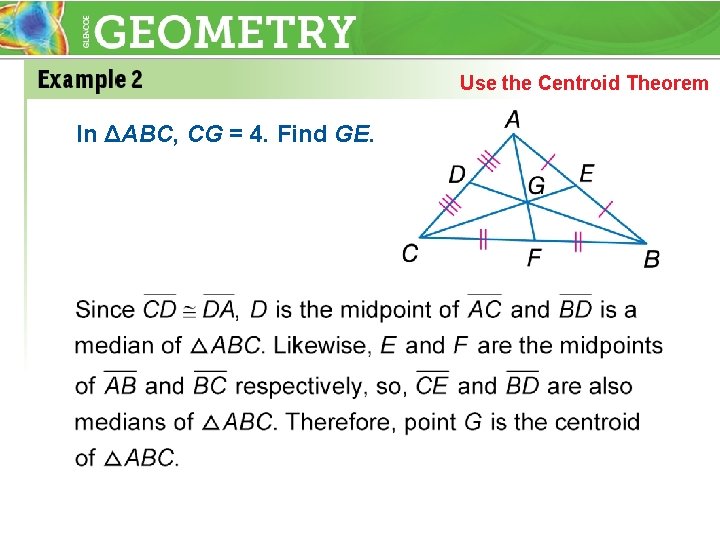
Use the Centroid Theorem In ΔABC, CG = 4. Find GE.

Use the Centroid Theorem CG = 4 6 = CE

Use the Centroid Theorem CG + GE = CE 4 + GE = 6 GE = 2 Answer: GE = 2 Segment Addition Substitution Subtract 4 from each side.

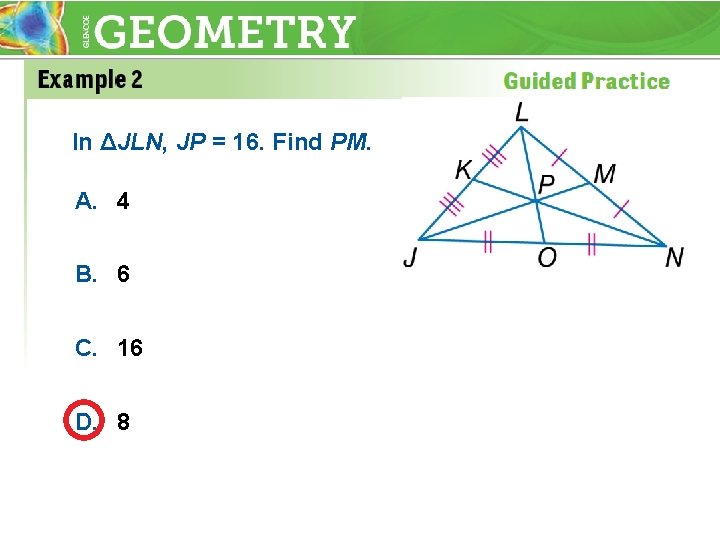
In ΔJLN, JP = 16. Find PM. A. 4 B. 6 C. 16 D. 8

Find the Centroid on a Coordinate Plane SCULPTURE An artist is designing a sculpture that balances a triangle on top of a pole. In the artist’s design on the coordinate plane, the vertices are located at (1, 4), (3, 0), and (3, 8). What are the coordinates of the point where the artist should place the pole under the triangle so that it will balance? Understand You need to find the centroid of the triangle. This is the point at which the triangle will balance.

Find the Centroid on a Coordinate Plan Graph and label the triangle with vertices at (1, 4), (3, 0), and (3, 8). Use the Midpoint Theorem to find the midpoint of one of the sides of the triangle. The centroid is two-thirds the distance from the opposite vertex to that midpoint. Solve Graph the triangle and label the vertices A, B, and C.

Find the Centroid on a Coordinate Plane Find the midpoint D of BC. Graph point D.

Find the Centroid on a Coordinate Plane Notice that is a horizontal line. The distance from D(3, 4) to A(1, 4) is 3 – 1 or 2 units.

Find the Centroid on a Coordinate Plane The centroid P is the centroid is the distance. So, (2) or units to the right of A. The coordinates are. P

Find the Centroid on a Coordinate Plane Answer: The artist should place the pole at the point Check the distance of the centroid from 1 (2) point D(3, 4). The centroid should be __ 3 2 units to the left of D. So, the coordinates or __ 3 of the centroid is.

BASEBALL A fan of a local baseball team is designing a triangular sign for the upcoming game. In his design on the coordinate plane, the vertices are located at (– 3, 2), (– 1, – 2), and (– 1, 6). What are the coordinates of the point where the fan should place the pole under the triangle so that it will balance? A. B. C. (– 1, 2) D. (0, 4)

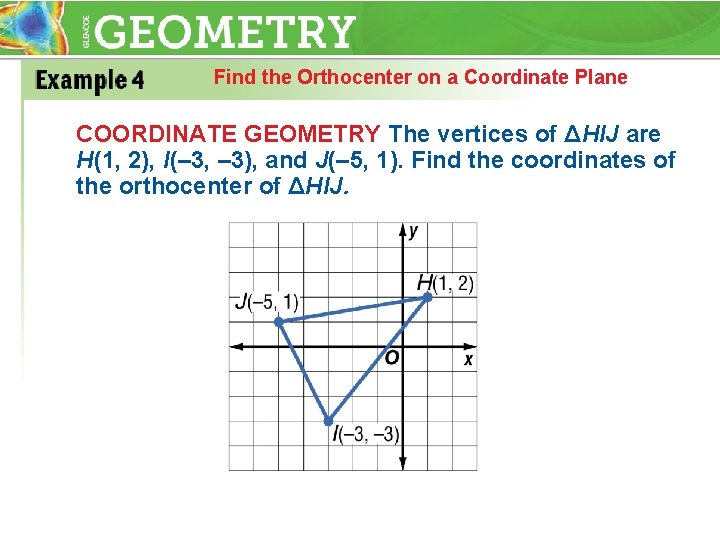
Find the Orthocenter on a Coordinate Plane COORDINATE GEOMETRY The vertices of ΔHIJ are H(1, 2), I(– 3, – 3), and J(– 5, 1). Find the coordinates of the orthocenter of ΔHIJ.

Find the Orthocenter on a Coordinate Plane Find an equation of the altitude from The slope of so the slope of an altitude is Point-slope form Distributive Property Add 1 to each side.

Find the Orthocenter on a Coordinate Plane Next, find an equation of the altitude from I to slope of The so the slope of an altitude is – 6. Point-slope form Distributive Property Subtract 3 from each side.

Find the Orthocenter on a Coordinate Plane Then, solve a system of equations to find the point of intersection of the altitudes. Equation of altitude from J Substitution, Multiply each side by 5. Add 105 to each side. Add 4 x to each side. Divide each side by – 26.

Find the Orthocenter on a Coordinate Plane Replace x with y-coordinate. in one of the equations to find the Rename as improper fractions. Multiply and simplify.

Find the Orthocenter on a Coordinate Plane Answer: The coordinates of the orthocenter of ΔHIJ are

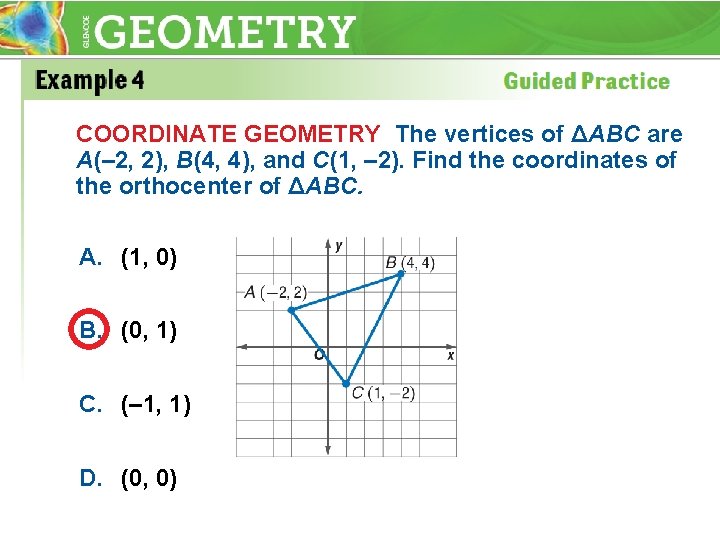
COORDINATE GEOMETRY The vertices of ΔABC are A(– 2, 2), B(4, 4), and C(1, – 2). Find the coordinates of the orthocenter of ΔABC. A. (1, 0) B. (0, 1) C. (– 1, 1) D. (0, 0)