Lerneinheit 19 Ausflle und Gewichtungen Ausflle Der im

Lerneinheit 19: Ausfälle und Gewichtungen Ausfälle Der im Erhebungsdesign einer Untersuchung festgelegte Auswahlplan lässt sich in der Regel nicht vollständig realisieren, da es in der Praxis praktisch unmöglich ist, alle Informationen über alle nach dem Auswahlplan zu erfassenden Elemente der Stichprobe zu erhalten. Es kommt somit zu Ausfällen (engl. : nonresponse). Bei den Auswirkungen von Ausfällen wird zwischen ignorierbaren Ausfällen und nichtignorierbaren Ausfällen unterschieden. Um den Unterschied zu verdeutlichen, wird das Beispiel der Schätzung des Anteils von Schülern weiterverfolgt, die Schule ohne Abschluss verlassen. Um die Zahl der möglichen Stichproben gering zu halten, wird nun davon ausgegangen, dass es in der Population 3 Schulen mit gleicher Anzahl von Schülern gibt, von denen zwei Schulen in einer einfachen Zufallsauswahl ausgewählt werden sollen. Schule 1 verlassen 10% der Schüler ohne Abschluss, Schule 2 verlassen 20% ohne Abschluss und Schule 3 30%. In der Population verlassen somit insgesamt 20% der Schüler die Schule ohne Abschluss. Dies ist der Wert, der aus den Stichprobendaten geschätzt werden soll. Zunächst wird wieder die Situation betrachtet, dass der Stichprobenplan (engl. : sampling frame) vollständig realisiert werden kann. Im Beispiel gibt es dann drei mögliche Stichproben, die mit gleicher Wahrscheinlichkeit realisiert werden. Empirie: Quantitative Methoden L 19 -1

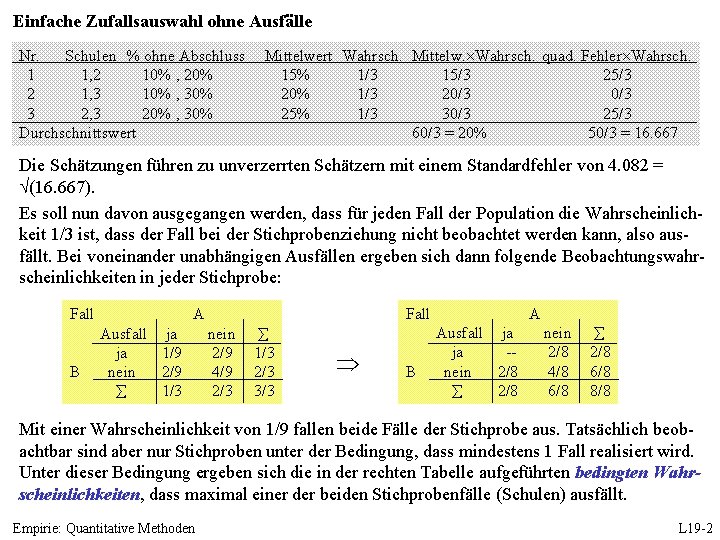
Einfache Zufallsauswahl ohne Ausfälle Nr. Schulen % ohne Abschluss 1 1, 2 10% , 20% 2 1, 3 10% , 30% 3 2, 3 20% , 30% Durchschnittswert Mittelwert Wahrsch. Mittelw. Wahrsch. quad. Fehler Wahrsch. 15% 1/3 15/3 20% 1/3 20/3 25% 1/3 30/3 25/3 60/3 = 20% 50/3 = 16. 667 Die Schätzungen führen zu unverzerrten Schätzern mit einem Standardfehler von 4. 082 = (16. 667). Es soll nun davon ausgegangen werden, dass für jeden Fall der Population die Wahrscheinlichkeit 1/3 ist, dass der Fall bei der Stichprobenziehung nicht beobachtet werden kann, also ausfällt. Bei voneinander unabhängigen Ausfällen ergeben sich dann folgende Beobachtungswahrscheinlichkeiten in jeder Stichprobe: Fall B Fall A Ausfall ja ja 1/9 nein 2/9 1/3 nein 2/9 4/9 2/3 1/3 2/3 3/3 B A Ausfall ja ja -nein 2/8 4/8 6/8 2/8 6/8 8/8 Mit einer Wahrscheinlichkeit von 1/9 fallen beide Fälle der Stichprobe aus. Tatsächlich beobachtbar sind aber nur Stichproben unter der Bedingung, dass mindestens 1 Fall realisiert wird. Unter dieser Bedingung ergeben sich die in der rechten Tabelle aufgeführten bedingten Wahrscheinlichkeiten, dass maximal einer der beiden Stichprobenfälle (Schulen) ausfällt. Empirie: Quantitative Methoden L 19 -2

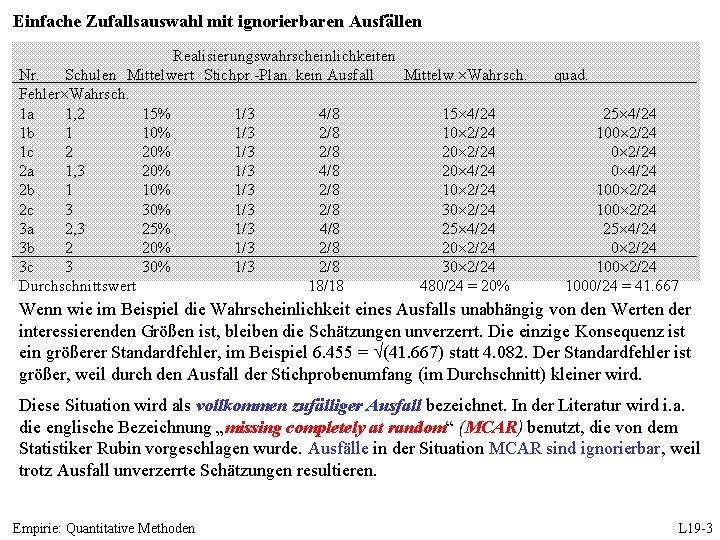
Einfache Zufallsauswahl mit ignorierbaren Ausfällen Realisierungswahrscheinlichkeiten Nr. Schulen Mittelwert Stichpr. -Plan. kein Ausfall Mittelw. Wahrsch. Fehler Wahrsch. 1 a 1, 2 15% 1/3 4/8 15 4/24 1 b 1 10% 1/3 2/8 10 2/24 1 c 2 20% 1/3 2/8 20 2/24 2 a 1, 3 20% 1/3 4/8 20 4/24 2 b 1 10% 1/3 2/8 10 2/24 2 c 3 30% 1/3 2/8 30 2/24 3 a 2, 3 25% 1/3 4/8 25 4/24 3 b 2 20% 1/3 2/8 20 2/24 3 c 3 30% 1/3 2/8 30 2/24 Durchschnittswert 18/18 480/24 = 20% quad. 25 4/24 100 2/24 0 4/24 100 2/24 25 4/24 0 2/24 1000/24 = 41. 667 Wenn wie im Beispiel die Wahrscheinlichkeit eines Ausfalls unabhängig von den Werten der interessierenden Größen ist, bleiben die Schätzungen unverzerrt. Die einzige Konsequenz ist ein größerer Standardfehler, im Beispiel 6. 455 = (41. 667) statt 4. 082. Der Standardfehler ist größer, weil durch den Ausfall der Stichprobenumfang (im Durchschnitt) kleiner wird. Diese Situation wird als vollkommen zufälliger Ausfall bezeichnet. In der Literatur wird i. a. die englische Bezeichnung „missing completely at random“ (MCAR) benutzt, die von dem Statistiker Rubin vorgeschlagen wurde. Ausfälle in der Situation MCAR sind ignorierbar, weil trotz Ausfall unverzerrte Schätzungen resultieren. Empirie: Quantitative Methoden L 19 -3

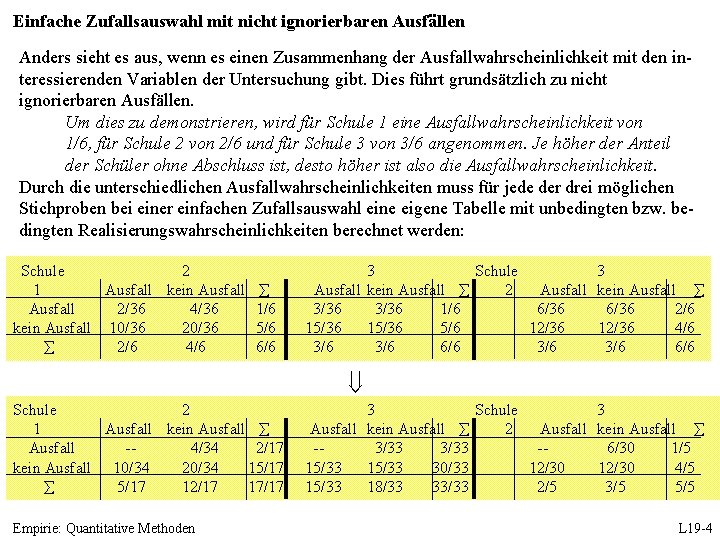
Einfache Zufallsauswahl mit nicht ignorierbaren Ausfällen Anders sieht es aus, wenn es einen Zusammenhang der Ausfallwahrscheinlichkeit mit den interessierenden Variablen der Untersuchung gibt. Dies führt grundsätzlich zu nicht ignorierbaren Ausfällen. Um dies zu demonstrieren, wird für Schule 1 eine Ausfallwahrscheinlichkeit von 1/6, für Schule 2 von 2/6 und für Schule 3 von 3/6 angenommen. Je höher der Anteil der Schüler ohne Abschluss ist, desto höher ist also die Ausfallwahrscheinlichkeit. Durch die unterschiedlichen Ausfallwahrscheinlichkeiten muss für jede der drei möglichen Stichproben bei einer einfachen Zufallsauswahl eine eigene Tabelle mit unbedingten bzw. bedingten Realisierungswahrscheinlichkeiten berechnet werden: Schule 2 1 Ausfall kein Ausfall 2/36 4/36 kein Ausfall 10/36 20/36 2/6 4/6 1/6 5/6 6/6 3 Schule 3 Ausfall kein Ausfall 2 Ausfall kein Ausfall 3/36 1/6 6/36 2/6 15/36 5/6 12/36 4/6 3/6 3/6 6/6 Schule 2 1 Ausfall kein Ausfall -4/34 2/17 kein Ausfall 10/34 20/34 15/17 12/17 17/17 Empirie: Quantitative Methoden 3 Schule 3 Ausfall kein Ausfall 2 Ausfall kein Ausfall -3/33 -6/30 1/5 15/33 30/33 12/30 4/5 15/33 18/33 33/33 2/5 3/5 5/5 L 19 -4

Einfache Zufallsauswahl mit nicht ignorierbaren Ausfällen Realisierungswahrscheinlichkeiten Nr. Schulen Mittelwert Stichpr. -Plan. kein Ausfall 1 a 1, 2 15% 1/3 10/17 1 b 1 10% 1/3 5/17 1 c 2 20% 1/3 2/17 2 a 1, 3 20% 1/3 15/33 2 b 1 10% 1/3 15/33 2 c 3 30% 1/3 3/33 3 a 2, 3 25% 1/3 2/5 3 b 2 20% 1/3 2/5 3 c 3 30% 1/3 1/5 Durchschnittswert Mittelw. Wahrsch. 15 10/51 = 2. 941 10 5/51 = 0. 980 20 2/51 = 0. 784 20 15/99 = 3. 030 10 15/99 = 1. 515 30 3/99 = 0. 909 25 2/15 = 3. 333 20 2/15 = 2. 667 30 1/15 = 2. 000 18. 160 quad. Fehler Wahrsch. 25 10/51 = 4. 902 100 5/51 = 9. 804 0 2/51 = 0 0 15/99 = 0 100 15/99 = 15. 152 100 3/99 = 3. 030 25 2/15 = 3. 333 0 2/15 = 0 100 1/15 = 6. 667 42. 888 Dadurch, dass die Ausfallwahrscheinlichkeiten nicht unabhängig von den Ausprägungen der interessierenden Variablen sind, sind die Schätzungen des Populationsmittelwerts verzerrt und der Ausfall daher nichtignorierbar. Innerhalb der nichtignorierbaren Ausfallsituationen gibt es wiederum zwei Möglichkeiten, die Rubin als „missing at random“ (MAR) bzw. „observed at random“ später als „missing not at random“ (MNAR) bezeichnet hat. Zur Charakterisierung dieser beiden Situationen muss zunächst zwischen dem vollständigen und dem teilweisen Ausfall einer Untersuchungseinheit unterschieden werden. Empirie: Quantitative Methoden L 19 -5

Unit-Nonresponse und Item-Nonresponse • Der vollständige Ausfall einer Untersuchungseinheit wird als Unit-Nonresponse bezeichnet, • der teilweise Ausfall bei einem oder mehreren Merkmalen als Item-Nonresponse. Bei Item-Nonresponse liegen also zumindest einige Informationen über einen Fall vor, bei dem allerdings andere interessierende Eigenschaften fehlen. Eine MAR-Situation liegt vor, wenn die Ausfallwahrscheinlichkeit bei einer Variablen nur von vorliegenden Informationen abhängt. Als Beispiel soll von einer zweiwelligen Panelstudie ausgegangen werden, bei der jeweils eine dichotome Variable, z. B. positive bzw. negative Beurteilung der Systemzufriedenheit, interessiert. Zur Verdeutlichung wird zunächst wieder von vollständigen Daten ohne Ausfall ausgegangen. Zu beiden Messzeitpunkten sind 2/3 mit dem politi. Systemzuschen System zufrieden, während 1/3 jeweils unzufriedenheit ja nein den ist. Welja 75 25 100 Allerdings wechseln - etwa als Folge von mangelnder le 2 nein 25 25 50 Reliabilität - zwischen den beiden Panelwellen jeweils 100 50 1/6 der Befragten ihre Beurteilung von zufrieden nach unzufrieden oder umgekehrt. Es wird nun angenommen, dass die in der ersten Welle systemzufriedenen Personen eine Ausfallwahrscheinlichkeit von 20% haben und die unzufriedenen Personen eine von 40%. Welle 1 Empirie: Quantitative Methoden L 19 -6

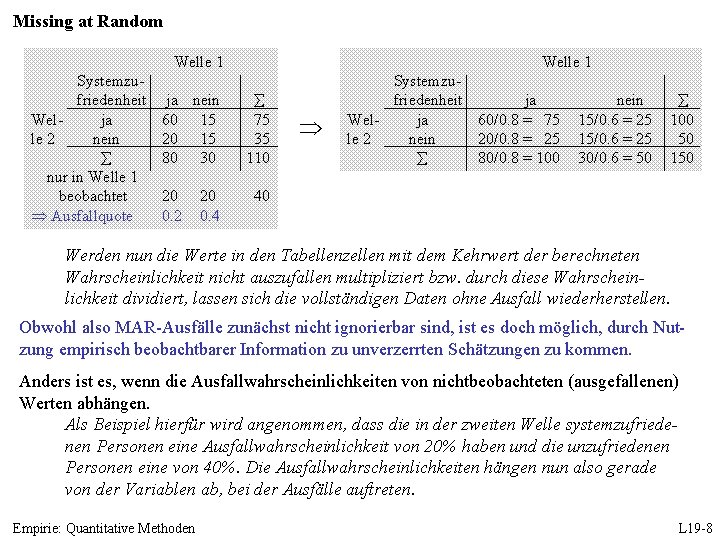
Missing at Random Welle 1 Systemzufriedenheit Welja le 2 nein nur in Welle 1 beobachtet ja nein 60 15 20 15 80 30 20 20 75 35 110 40 Durch den Ausfall reduziert sich die Zahl der Fälle bei den systemzufriedenen Personen von 100 auf 80. Die Zahl der in beiden Wellen zufriedenen Personen reduziert sich von 75 auf 60 (= 0. 8 75) und die der in Welle 1 zufriedenen und in Welle 2 unzufriedenen auf 20 (= 0. 8 25). Der Ausfall von 40% der in Welle 1 unzufriedenen Personen reduziert die Anzahl der in Welle 1 unzufriedenen und in Welle 2 zufriedenen Personen und der in beiden Wellen unzufriedenen Personen jeweils von 25 auf 15 (= 0. 6 25). Der Ausfall ist nicht ignorierbar, da im Unterschied zu den vollständigen Daten nun zwischen Welle 1 und 2 eine Reduktion des Anteils der Zufriedenen von 72. 7% (= 80/110) auf 68. 2% (= 75/110) zu beobachten ist. Diese Verzerrung kann jedoch relativ leicht kontrolliert werden, da die Ausfallwahrscheinlichkeit ausschließlich von vorhandenen Informationen abhängt. Da aus den vorliegenden Daten ersichtlich ist, dass jeweils 20 von ursprünglich 100 bzw. 50 in Welle 1 systemzufriedenen bzw. unzufriedenen Personen ausfallen, kann aus diesen Werten für die Zufriedenen eine Ausfallquote von 20% (= 20/100) und für die Unzufriedenen von 40% (= 20/50) berechnet werden. Empirie: Quantitative Methoden L 19 -7

Missing at Random Welle 1 Systemzufriedenheit Welja le 2 nein nur in Welle 1 beobachtet Ausfallquote ja nein 60 15 20 15 80 30 20 0. 2 20 0. 4 75 35 110 Systemzufriedenheit ja Welja 60/0. 8 = 75 le 2 nein 20/0. 8 = 25 80/0. 8 = 100 nein 15/0. 6 = 25 30/0. 6 = 50 100 50 150 40 Werden nun die Werte in den Tabellenzellen mit dem Kehrwert der berechneten Wahrscheinlichkeit nicht auszufallen multipliziert bzw. durch diese Wahrscheinlichkeit dividiert, lassen sich die vollständigen Daten ohne Ausfall wiederherstellen. Obwohl also MAR-Ausfälle zunächst nicht ignorierbar sind, ist es doch möglich, durch Nutzung empirisch beobachtbarer Information zu unverzerrten Schätzungen zu kommen. Anders ist es, wenn die Ausfallwahrscheinlichkeiten von nichtbeobachteten (ausgefallenen) Werten abhängen. Als Beispiel hierfür wird angenommen, dass die in der zweiten Welle systemzufriedenen Personen eine Ausfallwahrscheinlichkeit von 20% haben und die unzufriedenen Personen eine von 40%. Die Ausfallwahrscheinlichkeiten hängen nun also gerade von der Variablen ab, bei der Ausfälle auftreten. Empirie: Quantitative Methoden L 19 -8

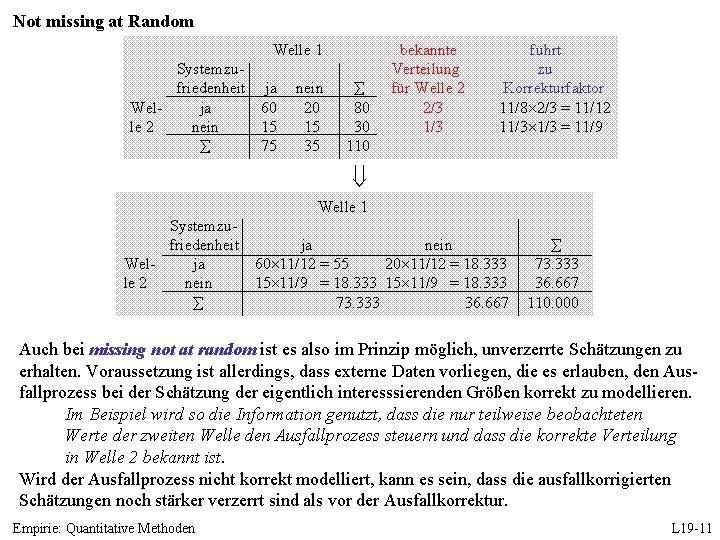
Not missing at Random Welle 1 Systemzufriedenheit Welja le 2 nein nur in Welle 1 beobachtet Ausfallquote ja 60 15 75 nein 20 15 35 80 30 110 25. 25 15. 30 40 Systemzufriedenheit ja nein Welja 60/. 75 = 80 20/0. 7 = 28. 6 le 2 nein 15/. 75 = 20 15/0. 7 = 21. 4 75/. 75 = 100 35/0. 7 = 50. 0 108. 6 41. 4 150. 0 Werden wieder wie im MAR-Beispiel aus den vorhandenen Informationen über die Ausfälle nach der 1. Welle Ausfallquoten berechnet und diese benutzt, um zu versuchen, die vollständigen Daten herzustellen, zeigt sich, dass dies nicht möglich ist: Die Zahl der Zufriedenen in Welle 2 wird über-, die der Unzufriedenen unterschätzt. Ausfällen, die weder MCAR noch MAR sind, sind nicht ignorierbar und es ist zudem nicht möglich, durch ausschließliche Nutzung vorliegender Information zu unverzerrten Schätzungen zu kommen. Unverzerrte Schätzungen sind hier nur möglich, wenn der Ausfallprozess bei der Schätzung korrekt berücksichtigt wird. Es bedarf daher zusätzlicher (externer) Informationen. Angenommen, es ist (durch andere Daten) bekannt, dass in der zweiten Welle, das Verhältnis von Zufriedenen zu Nichtzufriedenen 2 zu 1 beträgt. Empirie: Quantitative Methoden L 19 -9

Not missing at Random Welle 1 Systemzufriedenheit ja Welja 60 le 2 nein 15 75 nein 20 15 35 80 30 110 bekannte Verteilung für Welle 2 2/3 1/3 führt zu Korrekturfaktor 11/8 2/3 = 11/12 11/3 = 11/9 Welle 1 Systemzufriedenheit ja nein Welja 60 11/12 = 55 20 11/12 = 18. 333 le 2 nein 15 11/9 = 18. 333 73. 333 36. 667 110. 000 Aus dem Produkt des Kehrwerts aus der beobachteten Verteilung in Welle mal der bekannten tatsächlichen Verteilung für Welle 2 lassen sich Korrekturfaktoren berechen, deren Anwendung zu einer unverzerrten Schätzung der relativen Häufigkeiten führt: Für die rekonstruierten Daten gilt wie für die vollständigen Daten, dass sich das Verhältnis der systemzufriedenen zu den systemunzufrieden Personen nicht ändert und die Zahl der Wechsler von zufrieden zu unzufrieden bzw. umgekehrt jeweils gleich ist und 1/6 (=18. 333/110) der Fallzahl beträgt. Empirie: Quantitative Methoden L 19 -10

Not missing at Random Welle 1 Systemzufriedenheit ja Welja 60 le 2 nein 15 75 nein 20 15 35 80 30 110 bekannte Verteilung für Welle 2 2/3 1/3 führt zu Korrekturfaktor 11/8 2/3 = 11/12 11/3 = 11/9 Welle 1 Systemzufriedenheit ja nein Welja 60 11/12 = 55 20 11/12 = 18. 333 le 2 nein 15 11/9 = 18. 333 73. 333 36. 667 110. 000 Auch bei missing not at random ist es also im Prinzip möglich, unverzerrte Schätzungen zu erhalten. Voraussetzung ist allerdings, dass externe Daten vorliegen, die es erlauben, den Ausfallprozess bei der Schätzung der eigentlich interesssierenden Größen korrekt zu modellieren. Im Beispiel wird so die Information genutzt, dass die nur teilweise beobachteten Werte der zweiten Welle den Ausfallprozess steuern und dass die korrekte Verteilung in Welle 2 bekannt ist. Wird der Ausfallprozess nicht korrekt modelliert, kann es sein, dass die ausfallkorrigierten Schätzungen noch stärker verzerrt sind als vor der Ausfallkorrektur. Empirie: Quantitative Methoden L 19 -11

Ausfallgründe in Befragungen Zur Beurteilung der Qualität einer Stichprobe ist es sinnvoll, möglichst detaillierte Informationen über die Ausfallgründe von Unit-Nonresponse zu erhalten. Bei Befragungen werden daher Ausfallgründe regelmäßig mit erhoben. Dabei wird meist zwischen stichprobenneutralen und systematischen Ausfällen unterschieden, wobei für stichprobenneutrale Ausfälle unterstellt wird, dass sie irrelevant sind, d. h. missing completely at random (MCAR). Als unproblematische, stichprobenneutrale Ausfallgründe gelten etwa bei Telefonumfragen: • kein Anschluss unter gewählter Nummer, • technische Probleme (Störungen): hier wird unterstellt, dass technische Defekte nicht mit inhaltlichen Variablen einer Umfrage korreliert sind, • kein Privathaushalt (bei Befragung von Personen in Privathaushalten), • keine Zielperson im Privathaushalt (z. B. Ausländer bei Wahlumfragen), • statt Telefonanschluss Nummer für Fax oder Modem: wenn allerdings in einem Privathaushalt eine Nummer auch als Fax oder Modem genutzt wird, kann eine fälschliche Zuordnung als Fax oder Modem erfolgen. Empirie: Quantitative Methoden L 19 -12

Ausfallgründe in Befragungen Von kommerziellen Erhebungsinstituten werden oft auch die folgenden Gründe als stichprobenneutral bezeichnet: • kein Kontakt nach maximaler Anzahl von Kontaktversuchen, • Zielperson krank, • Zielperson über Erhebungszeitraum abwesend (z. B. verreist), • Zielperson trotz mehrerer Versuche nicht erreichbar. Problematisch ist diese Einteilung, weil Krankheit und Nichterreichbarkeit nicht gleichmäßig über die Bevölkerung verteilt sind und es daher nicht sicher ist, dass die Ausfälle bezogen auf die erhobenen Variablen tatsächlich MCAR sind. Systematische Ausfallgründe sind: • Hörer aufgelegt • keine Auskunft über mögliche Zielperson erhalten • Zielperson verweigert unter Hinweis auf fehlendes Interesse • Zielperson verweigert unter Hinweis auf keine Zeit • Zielperson verweigert unter Hinweis keine Auskunft am Telefon • Zielperson verweigert aus anderen Gründen Empirie: Quantitative Methoden L 19 -13

Ausfallgründe in Befragungen Die Ausschöpfungsquote berechnet sich aus dem Verhältnis der Anzahl der realisierten Fälle in der Stichprobe (Nettostichprobenumfang) zur Anzahl der nach dem Stichprobenplan auszuwählenden Elemente der Population (Bruttostichprobenumfang). Da in der Regel stichprobenneutrale Ausfälle von der Bruttostichprobe abgezogen werden und hier Spielraum besteht, ist die Ausschöpfungsquote nicht das Qualitätsmerkmal einer Erhebung, für das es oft gehalten wird. So ist durchaus eine gewisse Skepsis angebracht, wenn in Querschnittserhebungen der Wohnbevölkerung Ausschöpfungsquoten von 70 oder mehr Prozent berichtet werden. Realistischer dürften z. Z. Ausschöpfungsquoten zwischen 30 und 60 Prozent sein. Da Ausfälle die Realisierung des Stichprobenplans verhindern, können Ausfälle die Vorzüge von Zufallsauswahlen (statistische Repräsentativität) zunichte machen. So hat sich bei einigen Wahlumfragen gezeigt, dass etwa Quotenauswahlen innerhalb zufällig ausgewählter Gebiete nicht stets zu schlechteren Ergebnissen führen als (scheinbar) zufällige Random-Walks. Empirie: Quantitative Methoden L 19 -14

Gewichtungen Bei der Analyse von Daten wird jeder Fall standardmäßig so berücksichtigt, wie er beobachtet ist. Die Daten sind dann ungewichtet oder gleichgewichtet. Von gewichteten Daten spricht man, wenn den Fällen der Stichprobe unterschiedliche Gewichte zugeordnet werden und diese Gewichte in die Datenanalyse einfließen. So wurde in den Beispielen zum nicht ignorierbaren Ausfall die Werte in den Tabellenzellen mit unterschiedlichen Werten multipliziert. Das gleiche Ergebnis stellt sich ein, wenn bei der Situation „missing not at random“ jeder Fall, der in der zweiten Welle bei der Systemzufriedenheit die Ausprägung „zufrieden“ ausweist, das Gewicht 11/12 erhält, und jeder Fall mit der Ausprägung „unzufrieden“ das Gewicht 11/9 und dann die Berechnung mit gewichteten Daten durchgeführt wird. Das Beispiel zeigt, dass gewichtete Daten zu „besseren“ Schätzungen führen können als ungewichtete Daten. In der Praxis der Sozialforschung werden zwei Arten von Gewichten eingesetzt: • Designgewichte sind für unverzerrte Schätzungen notwendig, wenn der Stichprobenplan einer empirischen Erhebung die Zahl der Stichprobenfälle in den Schichten oder Klumpen nicht proportional zu den entsprechenden Populationszahlen vorsieht. So werden in Deutschland in Bevölkerungsumfragen in der Regel sehr viel mehr Befragte aus den neuen Bundesländern befragt, als es dem Bevölkerungsanteil entspricht. Dies ermöglicht genauere Ost-West-Vergleiche, verzerrt aber Schätzungen für Gesamtdeutschland. Empirie: Quantitative Methoden L 19 -15

Gewichtungen Als Ausgleich werden daher Designgewichte verwendet, die Befragten aus den neuen Ländern ein geringeres und Befragten aus den alten Ländern ein höheres Gewicht geben. Da in Umfragen i. a. nur eine Person pro Haushalt befragt wird, haben Befragte aus Mehrpersonenhaushalten notwendigerweise eine geringere Chance, in die Stichprobe zu gelangen als Befragte aus Einpersonenhaushalten. Designgewichte, die Anzahl der Zielpersonen im Haushalt berücksichtigen, gleichen dies aus. Designgewichte sind so konstruiert, dass sie proportional zum Kehrwert der Auswahlwahrscheinlichkeit eines Falles in der Stichprobe sind. Um nicht den Stichprobenumfang zu verändern wird zudem sichergestellt, dass die Summe der Gewichte gleich der Stichprobenfallzahl ist. • Gewichte werden darüber hinaus verwendet, um Ausfälle zu korrigieren. Diese Art von Gewichtung wird als Redressment bezeichnet. Statistisch gesehen handelt es sich um eine Poststratifizierung, (engl. : Post-Stratification), die Abweichungen zwischen Stichproben- und Populationsverteilungen bei den Gewichtungsvariablen verhindert. Das Beispiel zur Korrektur der Verzerrung bei Ausfällen missing not at random kann auch als Beispiel für ein Redressment interpretiert werden, als die Abweichung der empirischen Verteilung der Systemzufriedenheit von der Verteilung in der Population zum zweiten Messzeitpunkt korrigiert wird. Die Gewichte sind proportional zum Kehrwert der relativen Stichprobenhäufigkeiten mal den relativen Populationshäufigkeiten. Empirie: Quantitative Methoden L 19 -16

Gewichtungen Kommerzielle Umfrageinstitute benutzen Redressment, um sogenannte Repräsentativgewichte zu erzeugen. In die Berechnung der Gewichte fließen oft Region und Haushaltsgröße sowie Alter, Geschlecht und Schulbildung als Gewichtungsvariablen ein. Repräsentativgewichte sind also meist Kombinationen aus Designgewichtung und Poststratifizierung. Gewichte können Schätzungen verbessern. Dies ist allerdings an Voraussetzungen gebunden: • So sind Designgewichte zwar theoretisch notwendig, um bei disproportionalen Stichproben unverzerrte Schätzungen zu erhalten. Vorausgesetzt wird dabei allerdings, dass der Stichprobenplan auch realisiert wird, also nur Ausfälle vorkommen, die MCAR sind. In Umfragen zeigt sich meist, dass Einpersonenhaushalte schlechter erreichbar sind als Mehrpersonenhaushalte. Designgewichte, die ungleiche Haushaltsgrößen ausgleichen sollen, können daher bewirken, dass Einpersonenhaushalte stärker unterrepräsentiert werden als in den ungewichteten Daten. Die Gewichte verschlechtern dann die Schätzungen. In der Praxis werden daher Designgewichte oft mit Poststratifizierung kombiniert. • Gewichte zum Ausgleich von Ausfällen sind nur dann optimal, wenn sie den Ausfallprozess korrekt wiedergeben. Wenn also z. B. eine Altersgruppe in einer Stichprobe nicht so oft vorkommt wie in der Population und dies durch Gewichtung ausgeglichen wird, wird unterstellt, dass Empirie: Quantitative Methoden L 19 -17

Gewichtungen die Befragten, die nach dem Stichprobenplan in der Altersgruppe befragt werden sollten, aber nicht erreicht wurden, die gleiche Verteilung der Beobachtungswerte aufweisen wie die in dieser Altersgruppe tatsächlich Befragten. Statistisch gesehen bedeutet dies, dass die Ausfälle bezogen auf die Gewichtungsvariablen zwar nicht „completely missing at random“ aber doch „missing at random“ (MAR) sind. Wenn andere Variablen als die Gewichtungsvariable den Ausfallprozess beeinflussen, dann führt die Gewichtung zu um so besseren Schätzungen, je höher die Gewichtungsvariablen mit den Variablen korrelieren, die den Ausfallprozess beeinflussen. • Redressment über mehrere Variablen setzt Kenntnis über die gemeinsame Verteilung aller Gewichtungsvariablen in der Population voraus. Tatsächlich sind aber oft nur die getrennten univariaten Verteilungen der Gewichtungsvariablen bekannt. Mit spezifischen Rechenalgorithmen werden die Gewichte dann so bestimmt, dass alle univariaten Verteilungen der Gewichtungsvariablen reproduziert werden. Dies gilt aber nicht notwendigerweise für die gemeinsame (multivariate) Verteilung der Gewichtungsvariablen. Die Gewichte führen daher nicht notwendigerweise zu korrekter multivariaten Poststratifizierung. • Redressmentgewichte beziehen sich auf den Ausgleich von Unit-Nonresponse. Darüber hinaus gibt es jedoch meist auch Item-Nonresponse, der durch Repräsentativgewichte nicht berücksichtigt wird. Es ist nicht auszuschließen, dass Repräsentativitätsgewichte unvorteilhaft mit Variablen korrelieren, die den Item-Nonresponse beeinflussen, und daher die Schätzungen nicht verbessern, sondern verschlechtern. Empirie: Quantitative Methoden L 19 -18

Gewichtungen • Bei der Datenanalyse gewichteter Daten müsste berücksichtigt werden, dass sich durch die Gewichtung die Standardfehlern ändern. Tatsächlich wird dies in den meisten Analysen genauso wenig berücksichtigt wie ein komplexes geschichtetes mehrstufiges Stichprobendesign. Stattdessen wird bei vielen Datenanalysen von einer einfachen Zufallsauswahl ohne Ausfall ausgegangen, auch wenn diese Situation tatsächlich nicht vorliegt. Es gibt Alternativen zu Gewichtungen: • Wenn der Zusammenhang einer abhängigen Variable mit erklärenden Variablen interessiert, ergeben gewichtete Datenanalysen die gleichen Ergebnisse wie ungewichtete Analysen, wenn alle Gewichtungsvariablen als zusätzliche erklärende Variablen in die Analyse eingehen. Die Berechnung der Gewichte ist dann nicht notwendig. • In der Statistik werden zunehmend neue Verfahren entwickelt und in der Sozialforschung eingesetzt, die auf der Basis der verfügbaren Informationen die zusätzlichen Fehlermöglichkeiten durch Ausfälle abschätzen und zu korrigieren versuchen. Empirie: Quantitative Methoden L 19 -19

Literaturhinweise: • Schnell u. a. , 6. • Diekmann, B. IX. Empirie: Quantitative Methoden L 19 -20