Le Pierangiolate n 4 Dipartimento di Ingegneria della

Le Pierangiolate n. 4 Dipartimento di Ingegneria della Informazione e Scienze Matematiche Luca Chiantini presenta La ricorrenza di Petruzzo

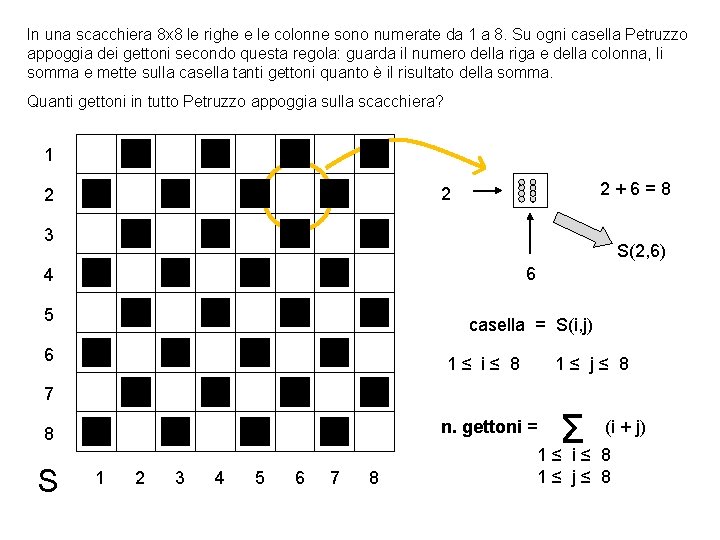
GIOCHI di ARCHIMEDE 2006 progetto olimpiadi UMI - Unione Matematica Italiana SNS - Scuola Normale Superiore PROBLEMA 11 In una scacchiera 8 x 8 le righe e le colonne sono numerate da 1 a 8. Su ogni casella Petruzzo appoggia dei gettoni secondo questa regola: guarda il numero della riga e della colonna, li somma e mette sulla casella tanti gettoni quanto è il risultato della somma. Quanti gettoni in tutto Petruzzo appoggia sulla scacchiera?

In una scacchiera 8 x 8 le righe e le colonne sono numerate da 1 a 8. Su ogni casella Petruzzo appoggia dei gettoni secondo questa regola: guarda il numero della riga e della colonna, li somma e mette sulla casella tanti gettoni quanto è il risultato della somma. Quanti gettoni in tutto Petruzzo appoggia sulla scacchiera? 1 2+6=8 2 2 3 S(2, 6) 6 4 5 casella = S(i, j) 6 1≤ i≤ 8 1≤ j≤ 8 7 (i + j) Σ 1≤ i≤ 8 n. gettoni = 8 S 1 2 3 4 5 6 7 8 1≤ j≤ 8

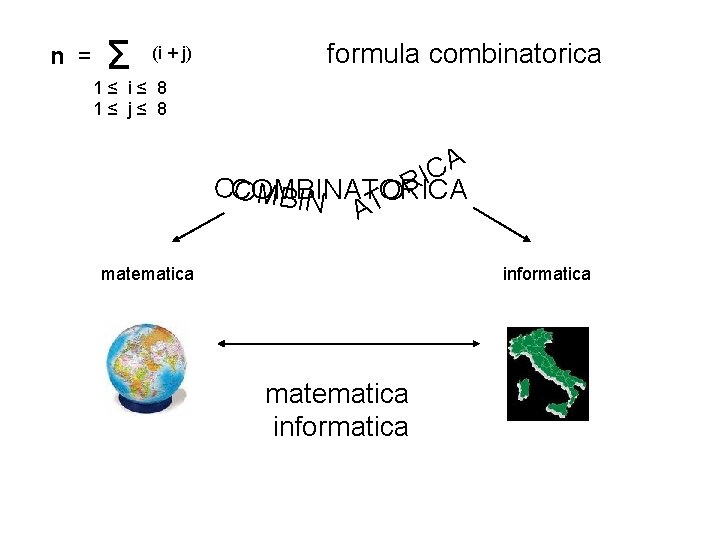
n = Σ (i + j) formula combinatorica 1≤ i≤ 8 1≤ j≤ 8 A C I R CCOMBINATORICA OMBIN O T A matematica informatica

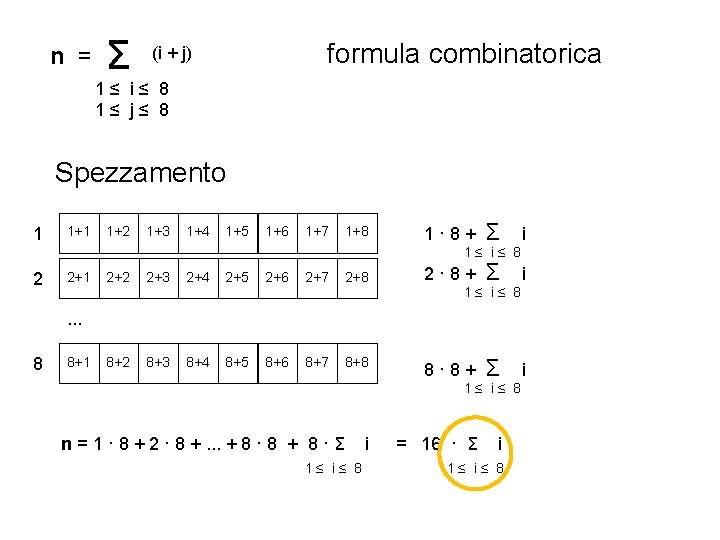
n = Σ formula combinatorica (i + j) 1≤ i≤ 8 1≤ j≤ 8 Spezzamento 1 1+2 1+3 1+4 1+5 1+6 1+7 1+8 1· 8+ Σ i Σ i 1≤ i≤ 8 2 2+1 2+2 2+3 2+4 2+5 2+6 2+7 2+8 2· 8+ 8+2 8+3 8+4 8+5 8+6 8+7 8+8 8· 8+ 1≤ i≤ 8 . . . 8 8+1 1≤ i≤ 8 n = 1 · 8 + 2 · 8 +. . . + 8 · 8 + 8 · Σ 1≤ i≤ 8 i = 16 · Σ i 1≤ i≤ 8

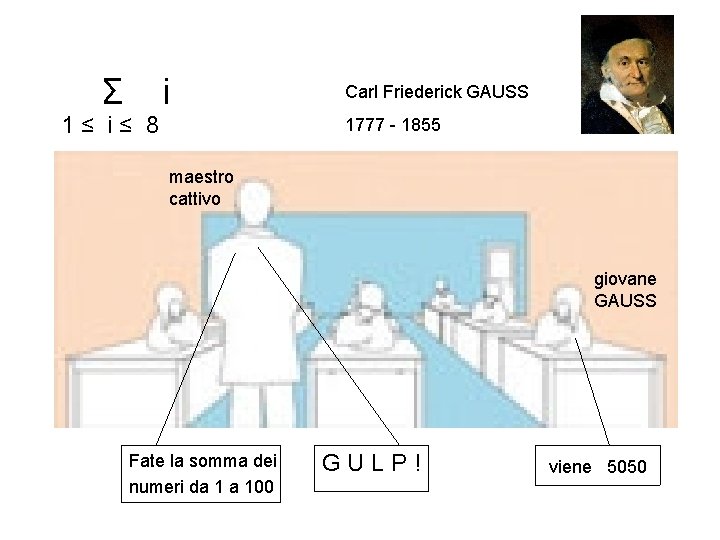
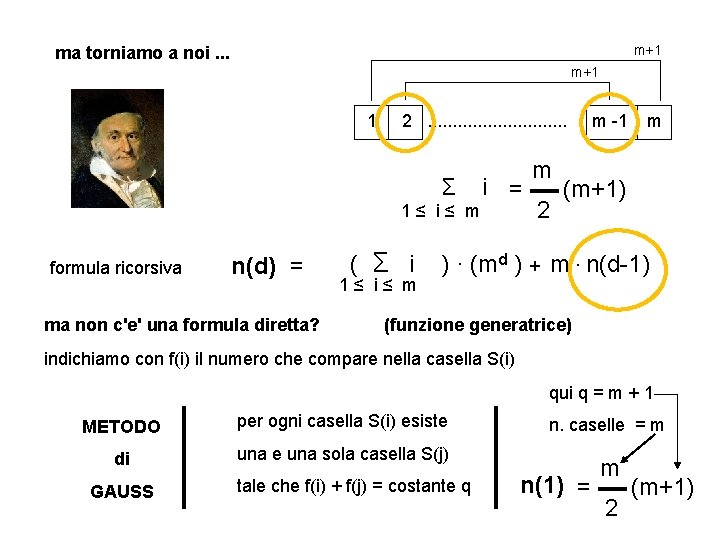
Σ 1≤ i≤ 8 i Carl Friederick GAUSS 1777 - 1855 maestro cattivo giovane GAUSS Fate la somma dei numeri da 1 a 100 GULP! viene 5050

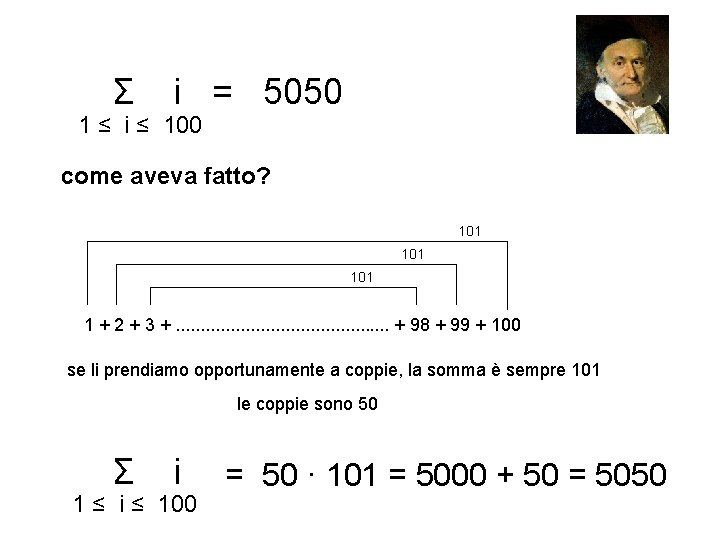
Σ i = 5050 1 ≤ i ≤ 100 come aveva fatto? 101 101 1 + 2 + 3 +. . . + 98 + 99 + 100 se li prendiamo opportunamente a coppie, la somma è sempre 101 le coppie sono 50 Σ i 1 ≤ i ≤ 100 = 50 · 101 = 5000 + 50 = 5050

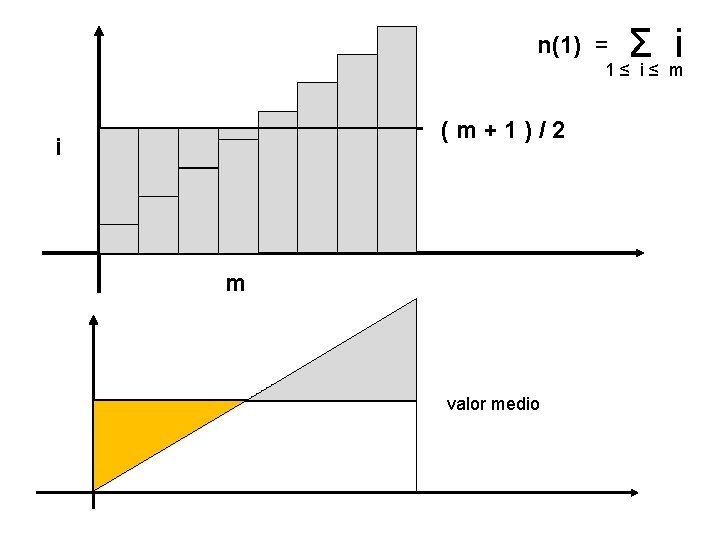
Σ i 1 ≤ i ≤ 100 = 50 · 101 = 5000 + 50 = 5050 9 9 1 + 2 +. . . . . + 7 + 8 Σ i = (8 : 2) · (8 + 1) = 4 · 9 = 36 i m = (m+1) 2 1≤ i≤ 8 e in generale Σ 1≤ i≤ m ATTENZIONE: m pari m dispari NB ? m (m+1) è sempre un numero intero 2

n = Σ formula combinatorica (i + j) 1≤ i≤ 8 1≤ j≤ 8 n = 1 · 8 + 2 · 8 +. . . + 8 · 8 Σ i + 8·Σ i = 16 · Σ i 1≤ i≤ 8 = (8 : 2) · (8 + 1) = 4 · 9 = 36 1≤ i≤ 8 n = 16 · Σ 1≤ i≤ 8 i = 16 · 36 = 576 Quanti gettoni in tutto Petruzzo appoggia sulla scacchiera? 576

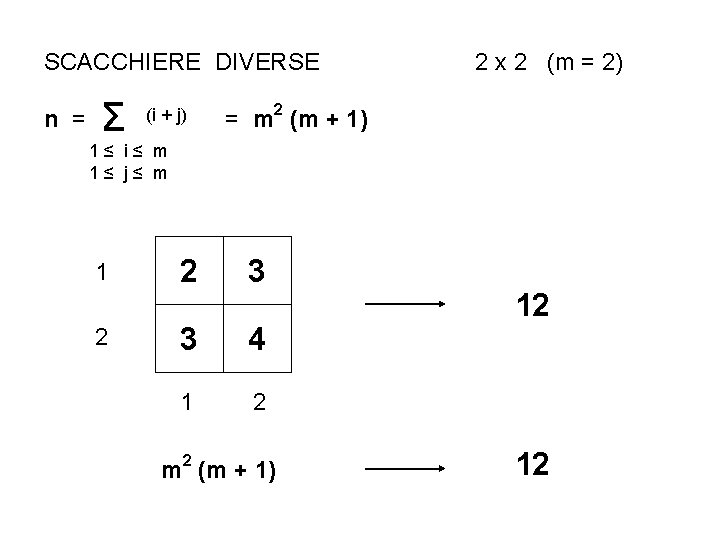
SCACCHIERE DIVERSE n = Σ (i + j) 2 x 2 (m = 2) = m 2 (m + 1) 1≤ i≤ m 1≤ j≤ m 1 2 2 3 3 4 1 2 m 2 (m + 1) 12 12

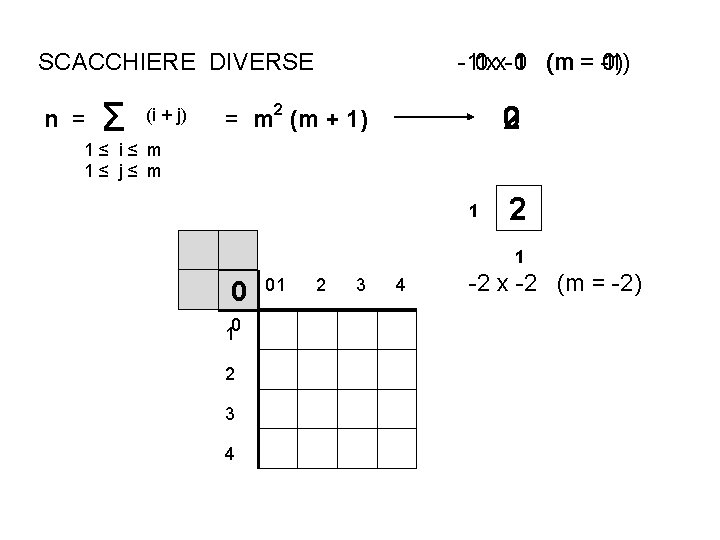
SCACCHIERE DIVERSE n = Σ (i + j) -11 0 xx-1 0 (m = -1) 1 0) 1) 2 0 = m 2 (m + 1) 1≤ i≤ m 1≤ j≤ m 1 2 1 0 10 2 3 4 01 2 3 4 -2 x -2 (m = -2)

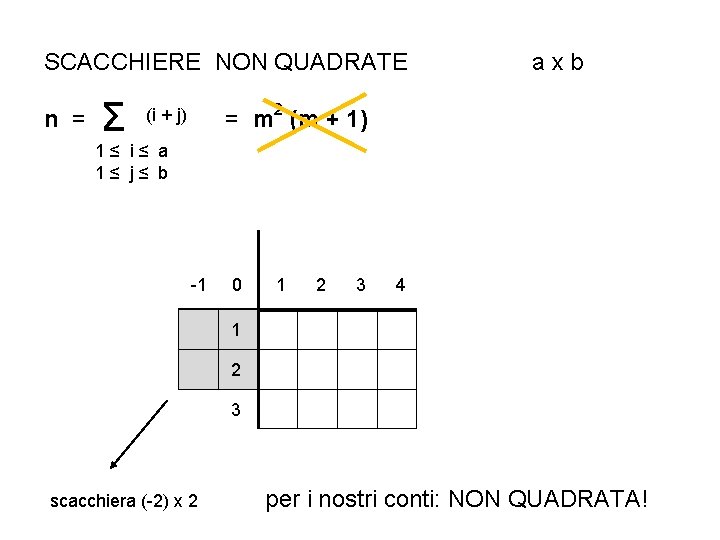
SCACCHIERE NON QUADRATE n = Σ axb = m 2 (m + 1) (i + j) 1≤ i≤ a 1≤ j≤ b -1 0 1 2 3 4 1 2 3 scacchiera (-2) x 2 per i nostri conti: NON QUADRATA!

"poesia della Matematica" ITALO CALVINO nato a Cuba 1923 morto a Siena 1985 Ultimo venne il Corvo (1946). . . Ad ogni sparo il soldato guardava il corvo: cadeva? No, girava sempre più basso. Forse il ragazzo non lo vedeva. Possibile? Forse il corvo non esisteva. Forse era solo una sua allucinazione. Forse chi sta per morire vede passare tutti gli uccelli e quando vede il corvo, vuol dire che è l'ora. . Le città invisibili (1972). . . MARCO non le contano MARCO Di Di una problema città non godi sette, olelesette, o le settantasette meraviglie, ma ma la la risposta che dà dà ad ad una tua domanda KAN O O le le domande che titi pone, costringendoti aa rispondere. Come Tebe, per bocca della Sfinge. . . .

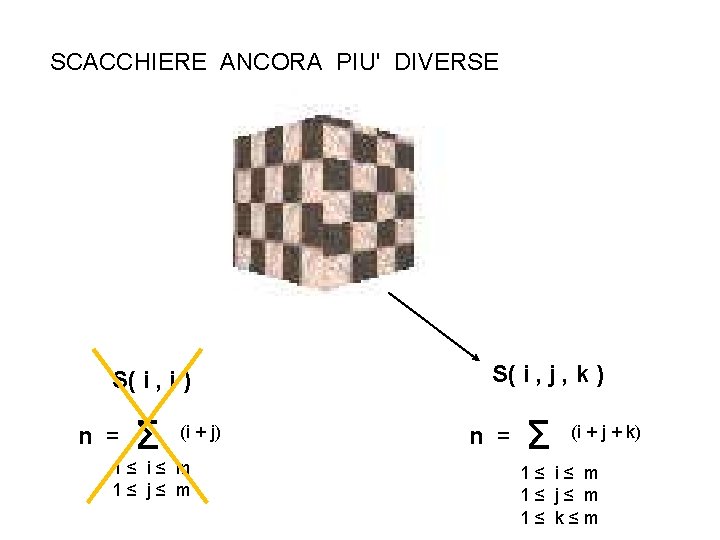
SCACCHIERE ANCORA PIU' DIVERSE S( i , j ) n = Σ (i + j) 1≤ i≤ m 1≤ j≤ m S( i , j , k ) n = Σ (i + j + k) 1≤ i≤ m 1≤ j≤ m 1≤ k≤m

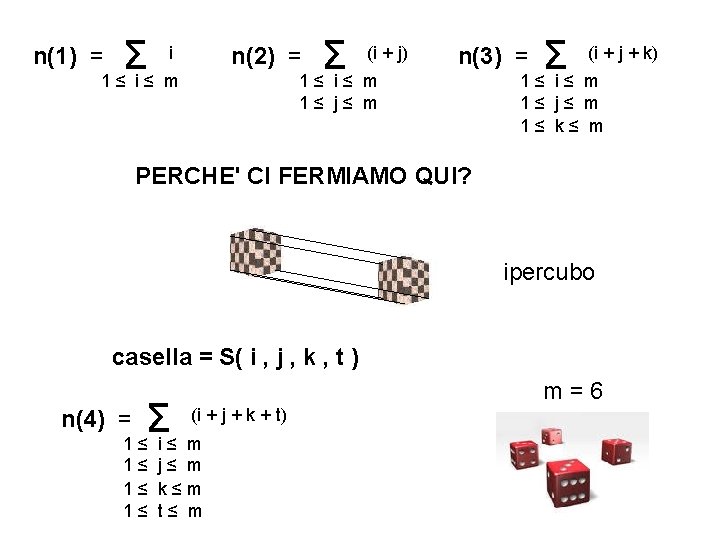
i Σ 1≤ i≤ m n(1) = (i + j) Σ 1≤ i≤ m n(2) = (i + j + k) Σ 1≤ i≤ m n(3) = 1≤ j≤ m 1≤ k≤ m PERCHE' CI FERMIAMO QUI? ipercubo casella = S( i , j , k , t ) (i + j + k + t) Σ 1≤ i≤ m n(4) = 1≤ j≤ m 1≤ k≤m 1≤ t≤ m m=6

i Σ 1≤ i≤ m n(1) = (i + j) Σ 1≤ i≤ m n(2) = (i + j + k) Σ 1≤ i≤ m n(3) = 1≤ j≤ m 1≤ k≤m dimensione: d casella = S( i 1 , . . . , id ) (i +. . . + i ) Σ 1≤ i ≤ m n(d) = 1 d q . . . Come era ovvio, come era necessario il rapporto dei lati del monolito, la sequenza 1 : 4 : 9! Arthur Clarke 2001: Odissea nello spazio E quale ingenuità avere immaginato che la sequenza terminasse a quel punto, con appena 3 dimensioni!. . .

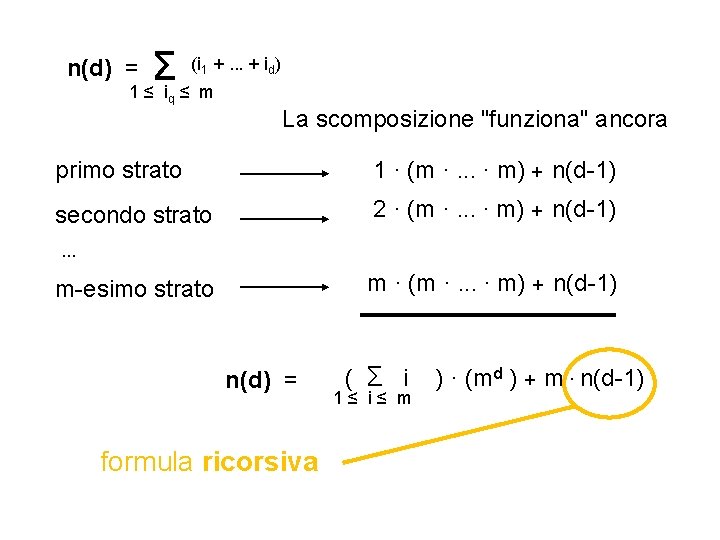
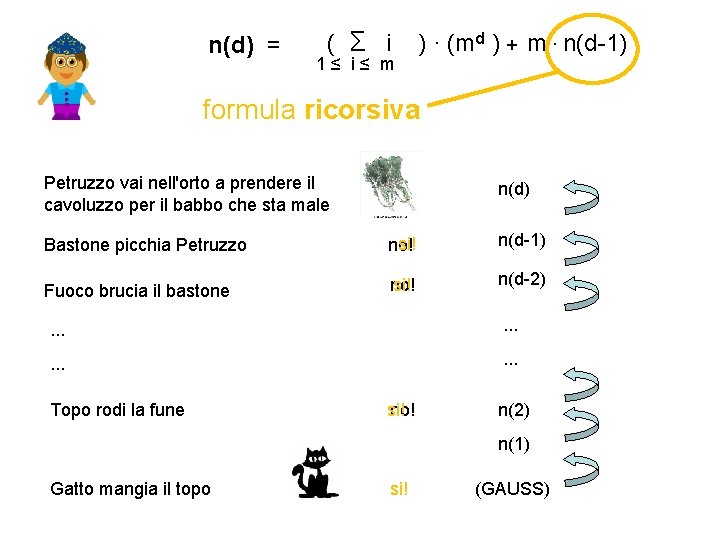
(i +. . . + i ) Σ 1≤ i ≤ m n(d) = 1 q d La scomposizione "funziona" ancora primo strato 1 · (m ·. . . ∙ m) + n(d-1) secondo strato 2 · (m ·. . . ∙ m) + n(d-1) . . . m · (m ·. . . ∙ m) + n(d-1) m-esimo strato n(d) = formula ricorsiva ( Σ i 1≤ i≤ m ) · (md ) + m · n(d-1)

n(d) = ( Σ i 1≤ i≤ m ) · (md ) + m · n(d-1) formula ricorsiva Petruzzo vai nell'orto a prendere il cavoluzzo per il babbo che sta male no! Bastone picchia Petruzzo si! no! n(d-1) Fuoco brucia il bastone no! si! n(d-2) n(d) . . . Topo rodi la fune si! no! n(2) n(1) Gatto mangia il topo si! (GAUSS)

Le città invisibili (1972). . . Il Kan cercava di immedesimarsi nel gioco, ma ora era il perchè del gioco a sfuggirgli. Quale era la posta? Allo scacco matto, sotto il piede del re sbalzato dal vincitore, non rimaneva che una casella vuota, un tassello di legno piallato: il nulla. . . Allora Marco parlò – La tua scacchiera, Sire, è intarsio di due legni: ebano e acero. Il tassello sul quale si fissa il tuo sguardo illuminato fu tagliato su uno strato del tronco che crebbe in un anno di siccità: vedi infatti come sono strette le fibre? Ecco un poro più grosso, indice di una malattia della pianta, che forse portò al suo abbattimento. . . – e continuava. Il Kan era stupito. La quantità di cose che si potevano leggere su un pezzetto di legno piallato lo sommergeva. E già Marco era venuto a parlare dei boschi di ebano, di zattere sui fiumi, e di approdi, e di donne alle finestre. . .

m+1 ma torniamo a noi. . . m+1 1 2. . . . Σ 1≤ i≤ m formula ricorsiva n(d) = ma non c'e' una formula diretta? ( Σ i 1≤ i≤ m i = m 2 m -1 m (m+1) ) · (md ) + m · n(d-1) (funzione generatrice) indichiamo con f(i) il numero che compare nella casella S(i) qui q = m + 1 METODO per ogni casella S(i) esiste di una e una sola casella S(j) GAUSS tale che f(i) + f(j) = costante q n. caselle = m n(1) = m 2 (m+1)

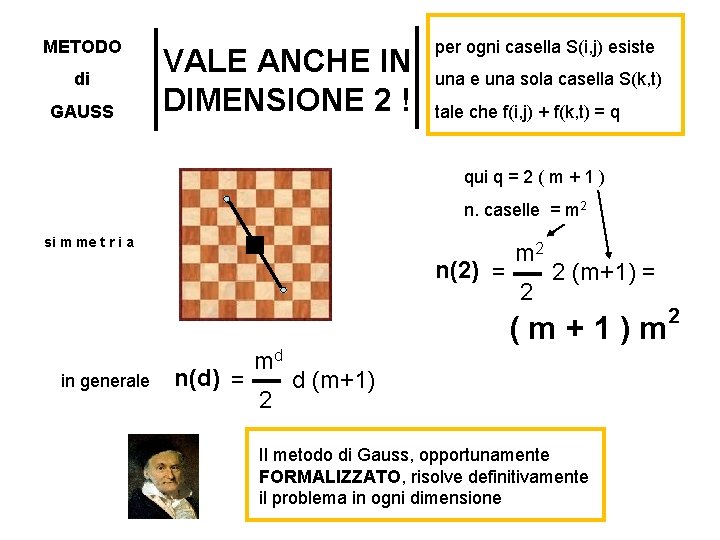
METODO di GAUSS VALE ANCHE IN DIMENSIONE 2 ! per ogni casella S(i, j) esiste una sola casella S(k, t) tale che f(i, j) + f(k, t) = q qui q = 2 ( m + 1 ) n. caselle = m 2 si m me t r i a n(2) = m 2 2 2 (m+1) = (m+1)m in generale n(d) = md 2 d (m+1) Il metodo di Gauss, opportunamente FORMALIZZATO, risolve definitivamente il problema in ogni dimensione 2

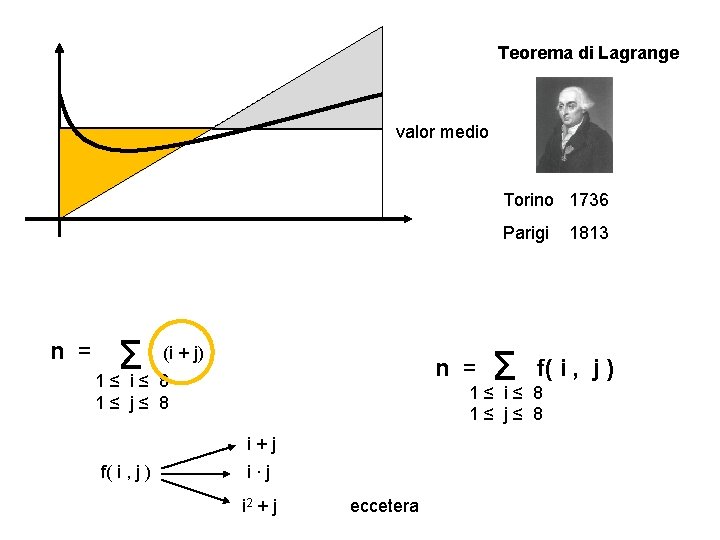
Σ i 1≤ i≤ m n(1) = (m+1)/2 i m valor medio

Teorema di Lagrange valor medio Torino 1736 Parigi n = (i + j) Σ 1≤ i≤ 8 f( i , Σ 1≤ i≤ 8 n = 1≤ j≤ 8 i+j f( i , j ) 1813 i∙j i 2 + j eccetera j)

Il metodo di Gauss, opportunamente FORMALIZZATO, risolve definitivamente il problema in ogni dimensione per ogni casella S(i, j) esiste una sola casella S(k, t) tale che f(i, j) + f(k, t) = q La FORMALIZZAZIONE è una componente essenziale della Matematica Quello che conta di un problema non sono le sette, o le settantasette meraviglie, ma la comprensione del suo schema, che permette non solo la sua soluzione, ma quasi sempre anche applicazioni molto più generali.

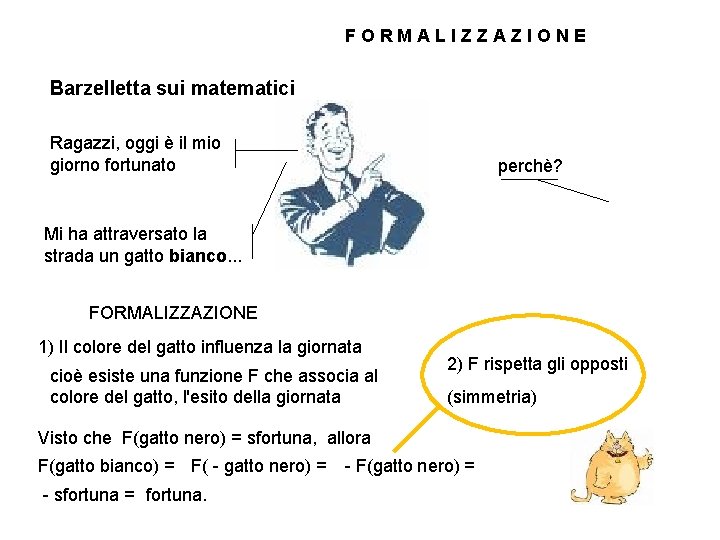
FORMALIZZAZIONE Barzelletta sui matematici Ragazzi, oggi è il mio giorno fortunato perchè? Mi ha attraversato la strada un gatto bianco. . . FORMALIZZAZIONE 1) Il colore del gatto influenza la giornata cioè esiste una funzione F che associa al colore del gatto, l'esito della giornata 2) F rispetta gli opposti (simmetria) Visto che F(gatto nero) = sfortuna, allora F(gatto bianco) = F( - gatto nero) = - F(gatto nero) = - sfortuna = fortuna.

Le città invisibili (1972) A Eudossia, città che si estende in alto e in basso, con vicoli tortuosi, scale, angiporti, si conserva un tappeto in cui puoi contemplare la forma della città A prima vista, nulla sembra assomigliare a Eudossia meno del tappeto. Ma se lo osservi con attenzione, ti persuadi che ad ogni suo punto corrisponde un luogo della città e viceversa, e le cose contenute nella città sono disposte nel tappeto, secondo i giusti rapporti, che sfuggono all'occhio distratto. Tutta la confusione di Eudossia, i ragli dei muli, le macchie di fumo, l'odore di pesce, è quanto appare nella prospettiva parziale che tu cogli. Ma il tappeto prova che c'è un punto dal quale la città mostra le sue vere sembianze. Sul rapporto che lega due oggetti così diversi come il tappeto e la città, fu interrogato un oracolo. "Uno dei due oggetti ha la forma che gli dettero al cielo stellato, l'altro ne è un riflesso approssimato, come ogni opera umana". I cittadini rimasero convinti che l'armonico disegno del tappeto fosse di natura divina. Così fu interpretato l'oracolo, senza dar luogo a contestazioni. Ma tu puoi trarre la conclusione opposta: che la vera mappa dell'Universo, appena riflessa nel tappeto, sia la città di Eudossia così com'è, una macchia informe con vie a zigzag, case che franano una sull'altra, incendi, urla nel buio.

Su un problema per le Olimpiadi, le dimensioni superiori, Petruzzo, i gatti neri e quant'altro. grazie per l'attenzione