Ksitteit ja mittaasteikot Petri Kainulainen Ksitteit Perusksitteit Perusjoukko

Käsitteitä ja mitta-asteikot Petri Kainulainen

Käsitteitä Peruskäsitteitä § Perusjoukko eli populaatio - tutkimuskohteiden muodostama joukko, josta tietoa halutaan kerätä § kaupungin asukkaat § Parkinsonin tautia sairastavat potilaat § yrityksessä valmistettavat tuotteet § Tilastoyksikkö eli havainto – perusjoukon yksi tutkimuskohde § kaupungin asukas § yritys § matkapuhelin § Muuttuja – mitattava ominaisuus, jota halutaan tutkia § työntekijän palkka § yrityksen liikkeenvaihto

Käsitteitä § Havaintoaineisto – muuttujien arvot, jotka saadaan mittaamalla tilastoyksikköjen ominaisuuksia Esim. 1 Havaintoaineisto nimi pituus paino kotipaikka -------------------------------------Ville 178 85 Kiuruvesi Seppo 182 84 Kalajoki Jaana 166 59 Vantaa § Otos – perusjoukon osa, jolta aineisto aiotaan kerätä § Jakauma – muuttujan arvojen jakautuminen mahdollisten arvojen joukossa. Voidaan havainnollistaa graafisesti esimerkiksi frekvenssikuvion avulla. § Tunnusluku – jakaumaa voidaan kuvailla tiivistetyssä muodossa (esim. keskiarvo)

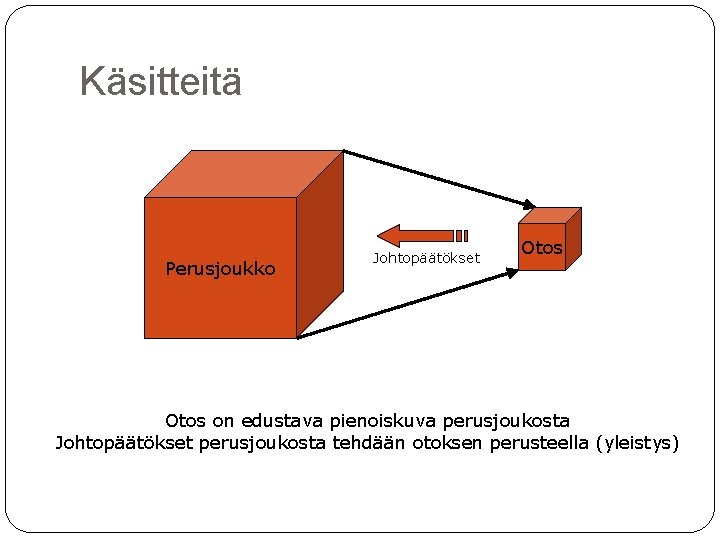
Käsitteitä Perusjoukko Johtopäätökset Otos on edustava pienoiskuva perusjoukosta Johtopäätökset perusjoukosta tehdään otoksen perusteella (yleistys)

Hyvän tutkimuksen vaatimukset ”Laadukas tutkimus voi olla hyvä investointi, joka tuo hintansa nopeasti takaisin. ” (lähde: Heikkilä: tilastollinen tutkimus) Validiteetti (pätevyys): Tutkimuksen pitää mitata sitä, mitä oli tarkoituskin selvittää. Kiinnitettävä siis huomiota mittareiden ja kysymysten valintaan. Reliabiliteetti (luotettavuus): Tarkoittaa tulosten tarkkuutta. Tulokset eivät saa olla sattumanvaraisia. Tulosten on oltava toistettavissa. Objektiivisuus (puolueettomuus): Tutkija ei saa omalla asenteellaan ja vakaumuksellaan vaikuttaa tutkimuksen kulkuun ja raportointiin.

Hyvän tutkimuksen vaatimukset Tehokkuus ja taloudellisuus: Kaikkiin tutkimuksiin ei aina liity taloudellisia vaatimuksia, mutta on turha tutkia sellaista, mikä on vain ”mukava tietää”. Avoimuus: Tutkittavien pitää tietää, mihin he ovat ryhtymässä. Kaikki tulokset esitellään niin kuin ne ovat. Menetelmät ja niiden puutteet kerrotaan. Tietosuoja: Kenenkään yksityisyys ei saa vaarantua. Hyödyllisyys ja käyttökelpoisuus: Tutkimuksen tulee tuoda esille jotain uutta, relevanttia tietoa. Sopiva aikataulu: Tietojen tulee olla käytössä silloin kun niitä tarvitaan.

Mittaaminen ja mitta-asteikot Yleistä mittaamisesta § Tilastollinen tutkimus on usein niin sanottua kvantitatiivista tutkimusta, johon liittyy ilmiöiden mittaaminen numeroiden avulla § Kvantitatiivisen tutkimuksen aineisto on yleensä numeerista § Lukuja (esim. pituus senteissä) § Monivalintakysymysten vastausvaihtoehtoja, jotka koodataan numeerisiksi (esim. 1 = nainen, 2 = mies) § Myös sanalliset ja kirjalliset tulokset voidaan muuttaa eli luokitella numeerisiksi § Sanallinen aineisto (teksti, ääni, kuva) on yleensä kvalitatiivisen (laadullinen) tutkimuksen aineistoa

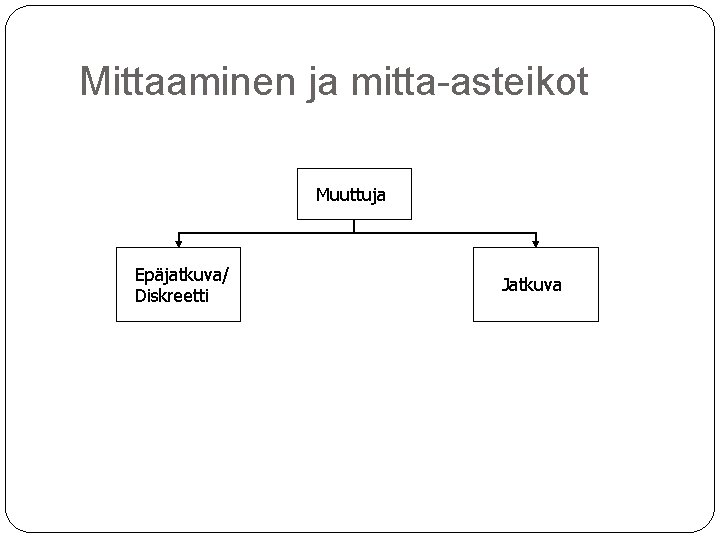
Mittaaminen ja mitta-asteikot Muuttuja Epäjatkuva/ Diskreetti Jatkuva

Mittaaminen ja mitta-asteikot Tilastollinen muuttuja on jatkuva, jos se voi saada minkä tahansa reaalilukuarvon tietyllä välillä (esim. paino, lämpötila) arvot pyöristetään usein (esim. kilogramma, aste) näin ilmoitettuna muuttujat eivät itse asiassa ole jatkuvia, mutta niitä käsitellään jatkuvina Muuttuja on epäjatkuva (diskreetti), jos se voi saada vain äärellisen määrän arvoja jollain tietyllä välillä laatua mittaavat muuttujat (esim. sukupuoli) lukumäärä on tyypillinen epäjatkuva muuttuja

Mittaaminen ja mitta-asteikot Mitta-asteikot § Muuttujille voidaan mittaustason mukaan määritellä mitta- asteikko § Mitta-asteikot määräytyvät sen mukaan, mitkä matemaattiset toimenpiteet (yhteen-, vähennys-, kerto- ja jakolasku) ovat sallittuja kyseisille muuttujille § Usein on teknisesti mahdollista suorittaa myös ”kiellettyjä” laskuoperaatioita § Mitta-asteikot on hyvä sisäistää, koska useiden tilastollisten laskentojen ja menetelmien soveltuvuus määräytyy mittaasteikon mukaan

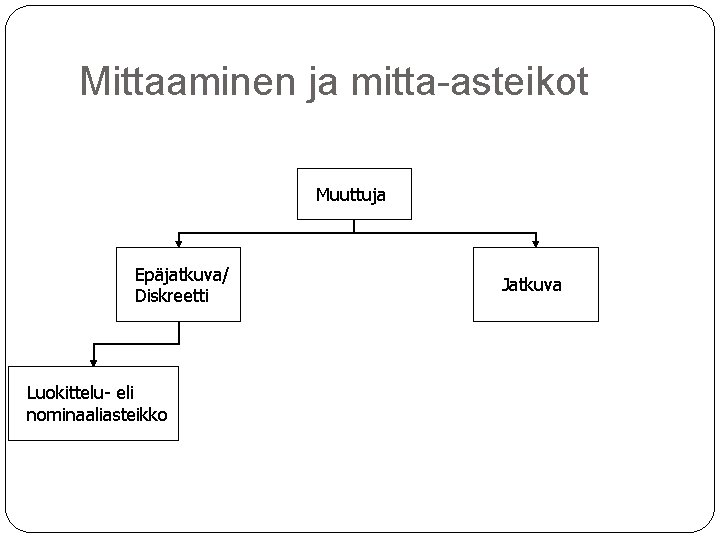
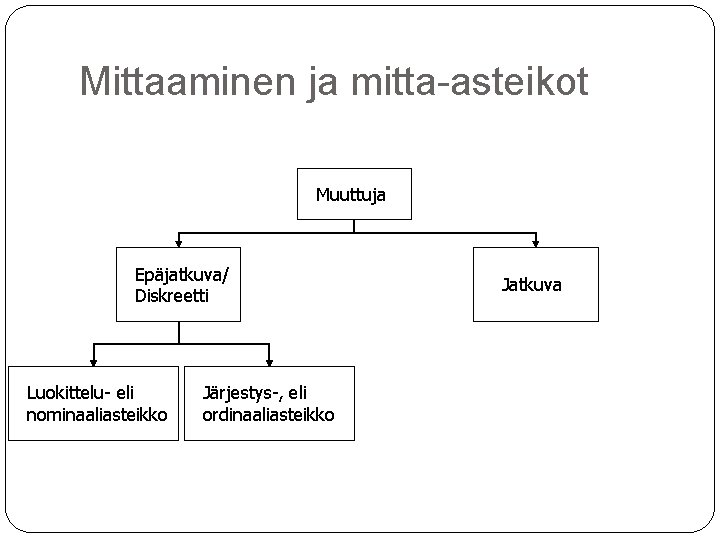
Mittaaminen ja mitta-asteikot Muuttuja Epäjatkuva/ Diskreetti Luokittelu- eli nominaaliasteikko Jatkuva

Mittaaminen ja mitta-asteikot Luokittelu- eli nominaaliasteikko ainoastaan luokittelu on sallittu operaatio mittaluku kertoo, mihin luokkaan kyseinen tilastoyksikkö kuuluu muuttujan luokkia ei voi asettaa järjestykseen esimerkkejä sukupuoli (nainen, mies) ammatti (poliisi, sairaanhoitaja, ATK-suunnittelija) asuinkunta (Vieremä, Kirkkonummi, Rovaniemi)

Mittaaminen ja mitta-asteikot Muuttuja Epäjatkuva/ Diskreetti Luokittelu- eli nominaaliasteikko Järjestys-, eli ordinaaliasteikko Jatkuva

Mittaaminen ja mitta-asteikot Järjestys- eli ordinaaliasteikko luokittelun lisäksi muuttujan mahdolliset arvot voidaan laittaa mitattavan ominaisuuden suhteen järjestykseen luokkien välisiä suuruuseroja ei voida määrittää peruslaskutoimitukset (esim. erotus) eivät ole sallittuja järjestys on otettava huomioon annettaessa luokille numerokoodit esimerkkejä määrä (ei ollenkaan, vähän, keskimääräisesti, paljon, erittäin paljon) ikäluokka (alle 30, 31 -40, 41 -50, 51 -60, yli 60)

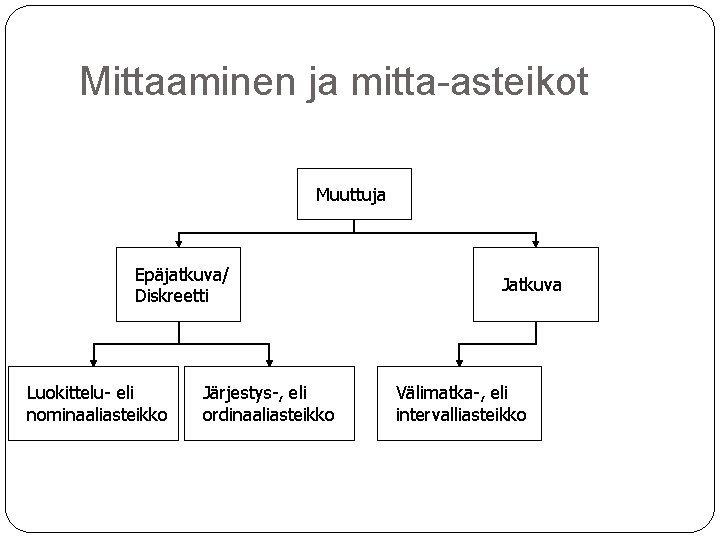
Mittaaminen ja mitta-asteikot Muuttuja Epäjatkuva/ Diskreetti Luokittelu- eli nominaaliasteikko Järjestys-, eli ordinaaliasteikko Jatkuva Välimatka-, eli intervalliasteikko

Mittaaminen ja mitta-asteikot Välimatka- eli intervalliasteikko sallittuja laskutoimituksia ovat vähennys- ja yhteenlasku absoluuttista nollakohtaa ei ole – se on sopimuksenvarainen esimerkkejä syntymävuosi lämpötila celsius-, tai fahrenheitasteina

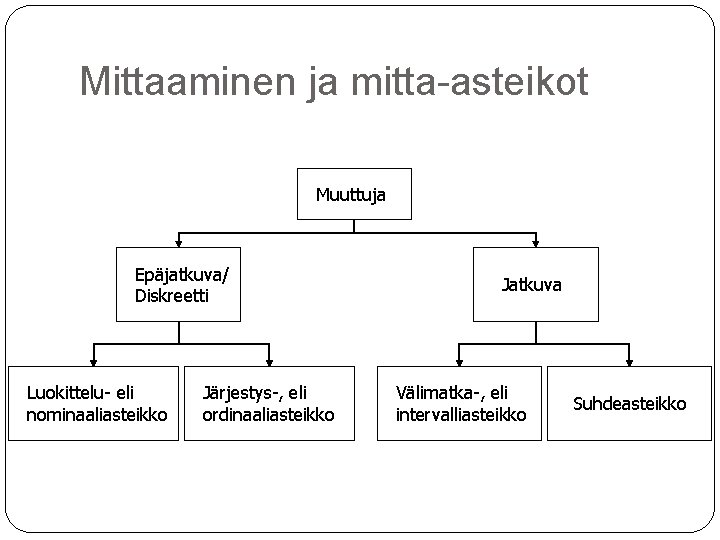
Mittaaminen ja mitta-asteikot Muuttuja Epäjatkuva/ Diskreetti Luokittelu- eli nominaaliasteikko Järjestys-, eli ordinaaliasteikko Jatkuva Välimatka-, eli intervalliasteikko Suhdeasteikko

Mittaaminen ja mitta-asteikot Suhdeasteikko sallitut laskutoimitukset ovat yhteen- ja vähennyslaskun lisäksi kerto- ja jakolasku intervalliasteikon vaatimusten lisäksi suhdeasteikon muuttujalla on absoluuttinen nollakohta, jossa tarkasteltava ominaisuus ”häviää” esimerkkejä ikä lämpötila Kelvinin asteikolla mitattuna pituus

Mittaaminen ja mitta-asteikot Edellä mainittujen lisäksi voidaan puhua absoluuttisesta asteikosta (esim. lukumäärien suhde) Aina muuttujasta ei voi yksikäsitteisesti sanoa, minkä mitta-asteikon vaatimukset se täyttää Mitta-asteikko vaikuttaa tilastollisen menetelmän valintaa – esimerkiksi keskiarvon käyttö vaatii vähintään välimatka-asteikollista muuttujaa