Tilastolliset tunnusluvut Petri Kainulainen Tilastolliset tunnusluvut Johdanto Frekvenssijakauma

Tilastolliset tunnusluvut Petri Kainulainen

Tilastolliset tunnusluvut Johdanto Frekvenssijakauma Jakauman sijaintiluvut Jakauman hajontaluvut Muunnokset

Tilastolliset tunnusluvut Johdanto Tilastollinen aineisto on usein hyvin laaja ja johtopäätösten tekeminen yksittäisiin havaintoihin perustuen vaikeaa ja jopa vaarallista Tilastollisilla tunnusluvuilla aineistoa kuvataan tiivistetyssä muodossa Keskiarvo luultavasti tutuin kaikista tilastollisista tunnusluvuista

Tilastolliset tunnusluvut Frekvenssijakauma § Käytetään kun halutaan tietää luokitellun muuttujan kunkin luokan havaintoyksiköiden lukumääriä ja osuuksia § Luokkia voivat olla esimerkiksi ammatti (poliisi, lääkäri, autonkuljettaja), opintojakson arvosana (1, 2, 3, 4, 5) § Jatkuva muuttuja voidaan luokitella (esim. pituus 140150, 151 -160, 161 -170, …)

Tilastolliset tunnusluvut Frekvenssi (fi) on luokan i havaintojen lukumäärä Suhteellinen frekvenssi (fi/n) on luokan i havaintojen osuus kaikista otoksen havainnoista (n) Summafrekvenssi (Fi = f 1 + f 2 + … + fi) kertoo, kuinka monella havainnolla muuttujan arvo on pienempi tai yhtä suuri kuin i: s luokka Suhteellinen summafrekvenssi kertoo, kuinka suuri osa koko havaintoaineistosta on pienempi tai yhtä suuri kuin kyseinen luokka èks esimerkit 2 ja 3

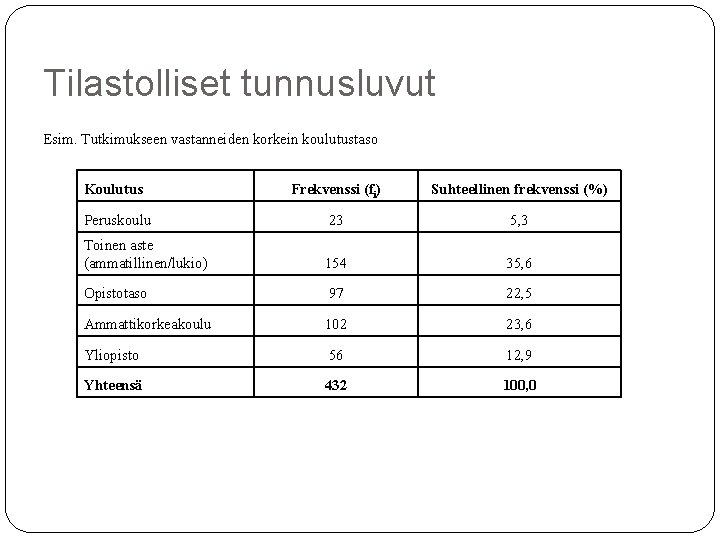
Tilastolliset tunnusluvut Esim. Tutkimukseen vastanneiden korkein koulutustaso Koulutus Frekvenssi (fi) Suhteellinen frekvenssi (%) Peruskoulu 23 5, 3 Toinen aste (ammatillinen/lukio) 154 35, 6 Opistotaso 97 22, 5 Ammattikorkeakoulu 102 23, 6 Yliopisto 56 12, 9 Yhteensä 432 100, 0

Tilastolliset tunnusluvut Esim. Tutkimukseen osallistuneiden ikä luokittain Ikä Suhteellinen summafrekvenssi Summafrekvenssi Frekvenssi Alle 20 109 0, 23 20– 30 145 254 0, 53 31– 40 162 416 0, 86 Yli 40 66 482 1, 00 Yhteensä 482

Tilastolliset tunnusluvut Jakauman sijaintiluvut § Jakauma kuvaa havaintoarvojen (esim. kuukausitulot) sijoittumista kaikkien mahdollisten arvojen joukossa § Jokaisen mitattavan muuttujan oletetaan noudattavan jotain jakaumaa § Jakaumia on hyvin monenlaisia, joista ehkä kuuluisin normaalijakauma (Gaussin käyrä, kellokäyrä) § Jakauman sijaintiluvuilla kuvataan sitä, mihin kohtaa jakaumaa havainnot sijoittuvat

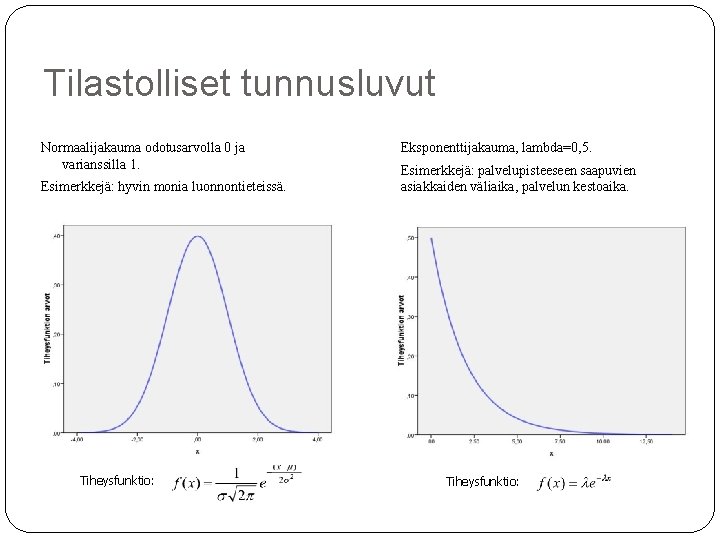
Tilastolliset tunnusluvut Normaalijakauma odotusarvolla 0 ja varianssilla 1. Esimerkkejä: hyvin monia luonnontieteissä. Tiheysfunktio: Eksponenttijakauma, lambda=0, 5. Esimerkkejä: palvelupisteeseen saapuvien asiakkaiden väliaika, palvelun kestoaika. Tiheysfunktio:

Tilastolliset tunnusluvut Χ 2 -jakauma vapausastein 3. Jatkuva tasajakauma välillä [1, 9]. Käytetään joissakin tilastollisissa testeissä. Kaikkien havaintojen todennäköisyys on yhtä suuri.

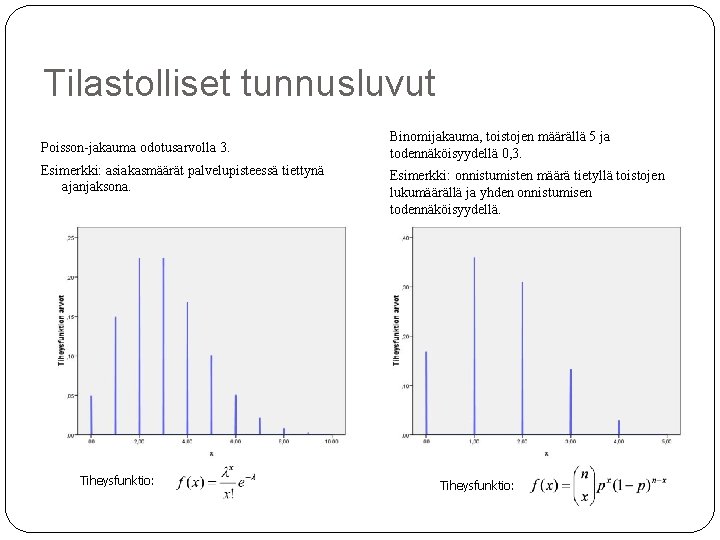
Tilastolliset tunnusluvut Poisson-jakauma odotusarvolla 3. Esimerkki: asiakasmäärät palvelupisteessä tiettynä ajanjaksona. Tiheysfunktio: Binomijakauma, toistojen määrällä 5 ja todennäköisyydellä 0, 3. Esimerkki: onnistumisten määrä tietyllä toistojen lukumäärällä ja yhden onnistumisen todennäköisyydellä. Tiheysfunktio:

Tilastolliset tunnusluvut Keskiarvo § Yleisin jakauman sijaintia kuvaava tunnusluku § Matemaattisin merkinnöin kirjoitettuna jossa xi on i: nnen havainnon arvo ja n havaintojen lukumäärä

Tilastolliset tunnusluvut Esim. Kymmenen työntekijän otoksesta saatiin seuraavanlaiset kuukausipalkat 1200, 1450, 1500, 1650, 1820, 2100, 2510, 2560, 2800, 3020. Lasketaan näiden palkkojen keskiarvo. Tämän perusteella voidaan todeta, että näiden henkilöiden palkka oli keskimäärin 2061 euroa kuukaudessa.

Tilastolliset tunnusluvut Mediaani (Md) § Yleinen jakauman paikkaa kuvaava tunnusluku varsinkin, jos jakauma on vino (esim. eksponenttijakautunut muuttuja) § Mediaani on suuruusjärjestykseen järjestetyn aineiston keskimmäinen havainto, jos havaintoja on pariton määrä --*--*-----*--*-*------*--*-------**-§ Jos havaintoja on parillinen määrä, mediaani on kahden keskimmäisen havainnon keskiarvo

Tilastolliset tunnusluvut Esim. Edellisen esimerkin kymmenen työntekijän otoksesta määritetään mediaani. Kuukausipalkat järjestetään ensin suuruusjärjestykseen. Kun havaintoja on parillinen määrä, mediaani on kahden keskimmäisen havainnon keskiarvo. 1200, 1450, 1500, 1650, 1820, 2100, 2510, 2560, 2800, 3020 Md = (1820 + 2100)/2 = 1960 Jos viimeinen havainto (3020) jätetään pois, havaintoja on pariton määrä ja tällöin mediaani on 1820.

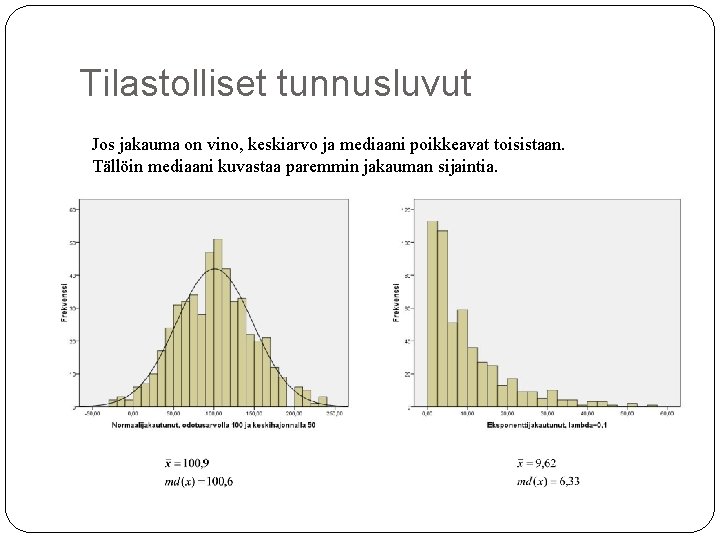
Tilastolliset tunnusluvut Jos jakauma on vino, keskiarvo ja mediaani poikkeavat toisistaan. Tällöin mediaani kuvastaa paremmin jakauman sijaintia.

Tilastolliset tunnusluvut Moodi eli tyyppiarvo (Mo) § Se muuttujan arvo, joita havaintoaineistossa on eniten § Useimmin esiintyviä arvoja voi olla useampia kuin yksi, tällöin moodi ei ole yksikäsitteinen § Voidaan määritellä jo luokka-asteen muuttujalle Esim. Kymmenen oppilaan otoksen matematiikan arvosanat jakautuivat seuraavasti: 5 6 7 7 8 8 9 9. Tällöin suurin määrä on numeron kahdeksan saaneita ja näin ollen moodi Mo=8.

Tilastolliset tunnusluvut Jakauman hajontaluvut § Keskiluvut eivät riitä osoittamaan, miten havainnot jakautuvat aineistossa (ei voida kuvata esim. palkkaeroja) § Havaintojen keskinäistä sijaintia ja jakautumista voidaan kuvata hajontaluvuilla § Usein kuvataan havaintojen jakautumista keskiarvon ympärille, mutta muitakin lukuja on käytössä § Hajontaa voidaan luonnehtia esim. seuraavalla tavalla ----------**-*-****---*-***------- ”pieni hajonta” --**----*----***-*-------*----**--- ”suuri hajonta”

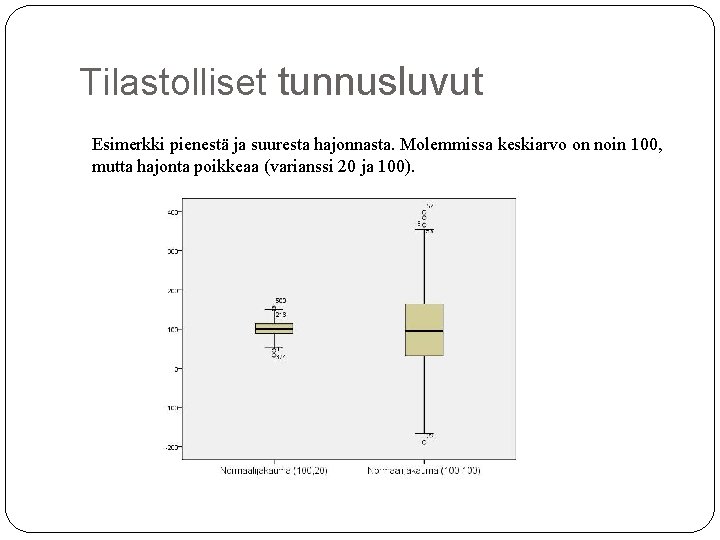
Tilastolliset tunnusluvut Esimerkki pienestä ja suuresta hajonnasta. Molemmissa keskiarvo on noin 100, mutta hajonta poikkeaa (varianssi 20 ja 100).

Tilastolliset tunnusluvut Vaihteluväli § Ulottuu havaintoaineiston pienimmästä arvosta suurimpaan arvoon § Ilmoitetaan kaarisulkuja käyttäen, luvut pilkulla (tai muulla vastaavalla) eroteltuna § Voidaan laskea myös vaihteluvälin pituus, joka on havaintoaineiston suurimman ja pienimmän arvon välinen erotus Esim. Vaihteluväli esimerkin 4 työntekijöiden palkoista on (1200, 3020) ja vaihteluvälin pituus 3020 – 1200 = 1820.

Tilastolliset tunnusluvut Keskihajonta eli standardipoikkeama (s) § Tärkein ja eniten käytetty hajonnan mitta § Käyttö sallittu vain suhde- ja välimatka-asteikon muuttujille § laskennassa otetaan huomioon se, miten kukin havainto poikkeaa keskiarvosta § Matemaattisin merkinnöin ilmaistuna jossa xi on i: nnen havainnon arvo ja n havaintojen lukumäärä

Tilastolliset tunnusluvut Esim. Kymmenen työntekijän otoksesta saadut palkat olivat 1200, 1450, 1500, 1650, 1820, 2100, 2510, 2560, 2800 ja 3020 euroa. Lasketaan näiden palkkojen keskihajonta. Keskiarvo ja keskihajonta voidaan ilmoittaa yhdessä seuraavasti: otoksen henkilöiden keskipalkka oli 2061 ± 630 euroa.

Tilastolliset tunnusluvut Keskihajonnan laskeminen edellä esitetyn kaavan avulla on monesti työlästä Keskihajonta voidaan myös laskea ilman keskiarvoa seuraavasti

Tilastolliset tunnusluvut Esim. Palkkojen keskihajonta laskettuna ilman keskiarvoa xi xi 2 -----------------1200 1440000 1450 2102500 1500 2250000 1650 2722500 1820 3312400 2100 4410000 2510 6300100 2560 6553600 2800 7840000 3020 9120400 -----------------20610 46051500

Tilastolliset tunnusluvut Variaatiokerroin (CV, V) § Variaatiokerroin on mittayksiköistä riippumaton hajonnan mitta § Muuttujan tulee olla suhdeasteikollinen § Kerrotaan usein sadalla, jolloin saatu luku CV% kertoo montako prosenttia keskihajonta on otoksen keskiarvosta § Variaatiokerroin on keskihajonnan ja keskiarvon suhde Esim. Aikaisempien esimerkkien otoksen henkilöiden palkan variaatiokerroin on

Tilastolliset tunnusluvut Muita jakauman sijaintia ja hajontaa kuvaavia tunnuslukuja § Fraktiilit – p%: n fraktiili on arvo, jota pienempiä on p% havainnoista § Kvartiilipoikkeama – kuinka pitkällä välillä aineiston ”keskellä” olevat 25% havainnoista sijaitsevat § Mediaanipoikkeama – keskihajonnan tyyppinen, mutta mittaa sitä kuinka havainnot poikkeavat mediaanista § Varianssi – keskihajonnan toinen potenssi, jolla on suuri merkitys tilastotieteen teoriassa

Tilastolliset tunnusluvut Muunnokset § Useat tilastolliset testit (t-testi, varianssianalyysi, regressioanalyysi) edellyttävät havaintojen noudattavan normaalijakaumaa § Vaikka alkuperäiset havainnot eivät tätä ehtoa täyttäisikään, voidaan tilannetta yrittää korjata erilaisten muunnoksien avulla § Muunnettuihin arvoihin perustuvien testien tulosten tulkinta ei ole aina yksinkertaista § Tärkeimpiä muunnoksia ovat § logaritmimuunnos § neliöjuurimuunnos § arvojen normitus keskiarvoon nolla ja varianssiin yksi