Kapitel 3 Zeichen und Zahlen n Auch wenn

Kapitel 3 Zeichen und Zahlen n Auch wenn Objekte der realen Welt beliebig komplex in Zusammensetzung uns Struktur sind, so werden sie in den meist auf zwei einfache Repräsentationen - als Abstraktion - abgebildet: Zeichen und Zahlen. Dieses Kapitel beschreibt, wie diese Objekte in eine für den Rechner verarbeitbare Form kodiert werden können. n Inhalt 1. Kodierung von Zeichen 2. Darstellung von Zahlen

3. 1 Kodierung von Zeichen n Die Wurzeln der Informatik liegen in der Mathematik. Die ersten „Computer“ waren Rechner im wörtlichen Sinne, deren Aufgabe die Verarbeitung von Zahlen war. Mittlerweile hat sich der Aufgabenschwerpunkt in Richtung „Elektronischer Datenverarbeitung“ verschoben, wobei als Datum immer weniger Zahlen im Mittelpunkt stehen, als vielmehr Texte. Dieses Unterkapitel beschreibt verschiedene Möglichkeiten die „Atome“ eines Textes, die Buchstaben, zu kodieren. n Inhalt n ASCII n EBCDIC n UNICODE

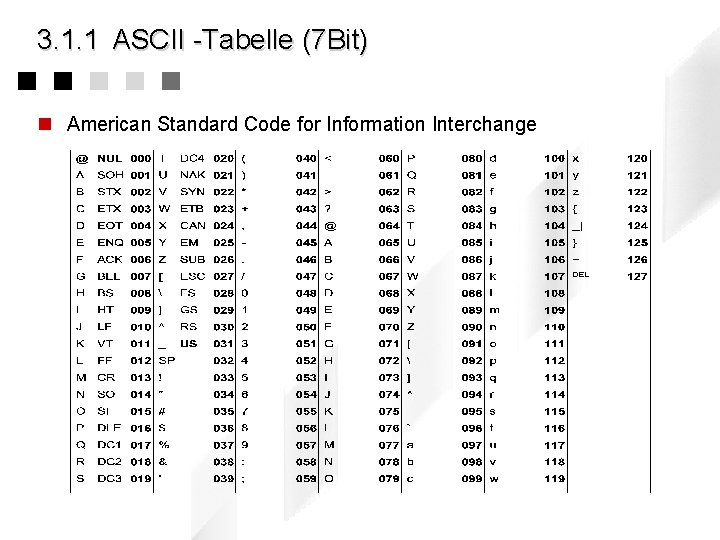
3. 1. 1 ASCII -Tabelle (7 Bit) n American Standard Code for Information Interchange

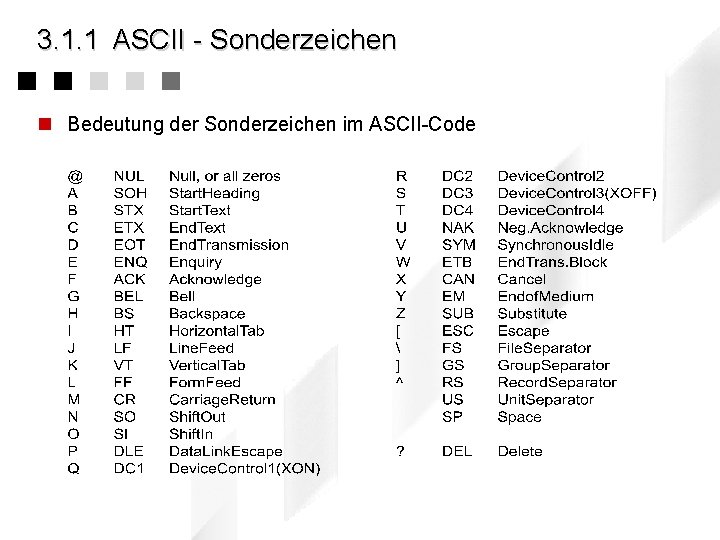
3. 1. 1 ASCII - Sonderzeichen n Bedeutung der Sonderzeichen im ASCII-Code

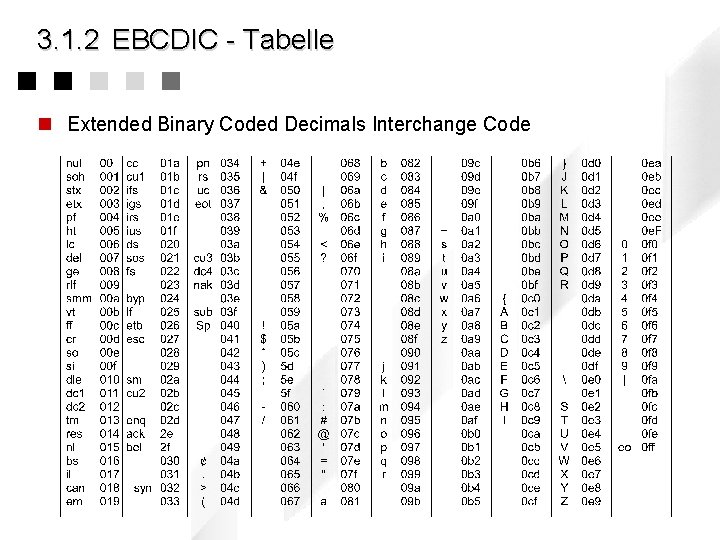
3. 1. 2 EBCDIC - Tabelle n Extended Binary Coded Decimals Interchange Code

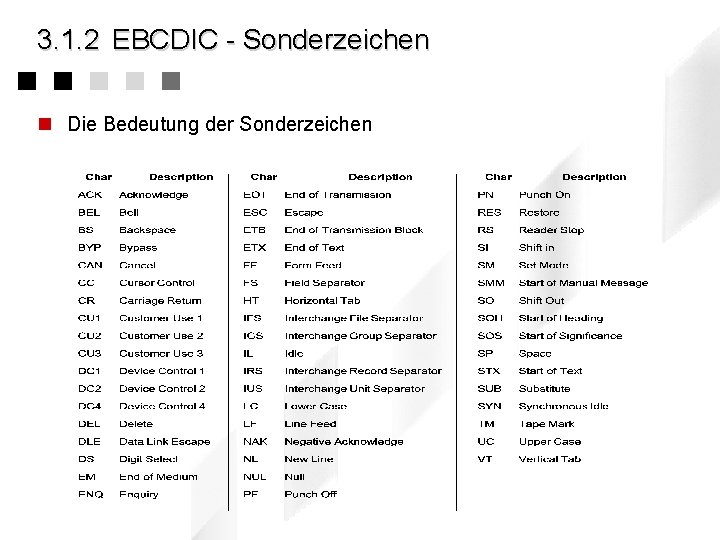
3. 1. 2 EBCDIC - Sonderzeichen n Die Bedeutung der Sonderzeichen

3. 1. 3 Unicode n Aktuelle Version 4. 0. 0 (siehe auch www. unicode. org) n Buchstaben und Symbole aus allen wichtigen geschriebenen Sprachen der Welt n n Amerika, Europa, Mittlerer Osten, Afrika, Indien, Asien, Pazifik Symbole Satzzeichen Sonderzeichen n Wird genormt in ISO/IEC 10646 n Kompatibilität mit ASCII n 0000 - 007 F: identisch mit 7 -bit ASCII n 007 F - 00 FF: Latin-1 Supplement (nationale Sonderbuchstaben) n 2500 - 25 FF: Blockgraphikzeichen (Box Drawing: ╘╚╞╬└┴├. . . )

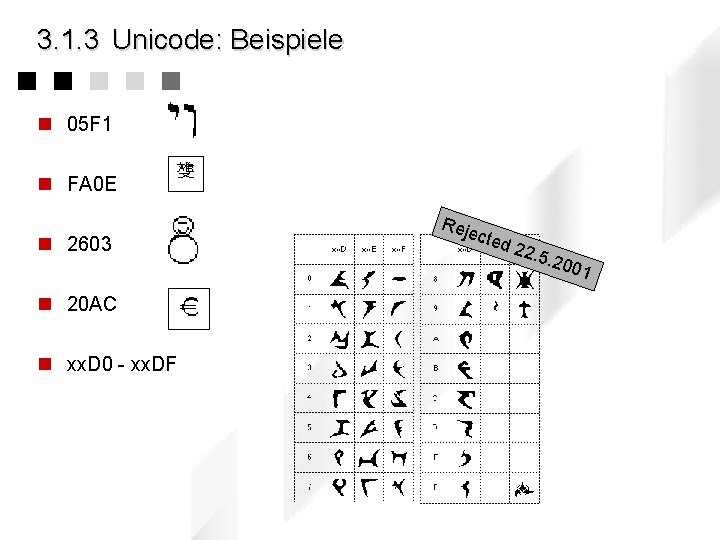
3. 1. 3 Unicode: Beispiele n 05 F 1 n FA 0 E n 2603 n 20 AC n xx. D 0 - xx. DF Reje cted 22. 5 . 200 1

3. 2 Darstellung von Zahlen n Die Darstellung von Zahlen spielt in der Informatik nach wie vor eine wichtige Rolle. Dabei gibt es unterschiedliche Mengen von Zahlen und auch unterschiedliche Operationen auf Zahlen. Dieses Unterkapitel beschreibt die Grundlagen der Zahlenkodierung, gibt für alle Mengen von Zahlen eine konkrete Kodierung an und führt in die Computerarithmetik ein. n Inhalt 1. 2. 3. 4. 5. 6. 7. 8. Zahlensysteme Konvertierung Arithmetik Ganze positive Zahlen Ganze negative Zahlen Gebrochene Zahlen Gleitpunktzahlen Standards

3. 2. 1 Zahlensysteme n Nicht systematische Zahlendarstellungen, z. B. : n Strichliste: I, III, IIII, IIII I, . . . n römische Zahlen: MIM, IX, . . n Systematische Zahlendarstellungen in einem Stellenwertsystem n Jede Zahl N läßt sich als Sequenz von Zeichen a i darstellen n Die Anzahl der notwendigen unterscheidbaren Zeichen ist B n N = S a i * B i n Im Dezimalsystem ist B = 10 und die unterscheidbaren Zeichen sind: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 n Im Binärsystem ist B = 2 und die unterscheidbaren Zeichen sind: 0, 1

3. 2. 1 Zahlensysteme - Beispiele n Dezimalsystem: n 199910 = 1*103 + 9*102 + 9*101 + 9*100 n Binärsysten: n 199910 = 1*210+1*29+1*28+1*27+1*26+1*23+1*22+1*21+1*20 111110011112 n Hexadezimalsystem (Sedezimalsystem) n Zeichen: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F n 199910 = 7*162 + 11*161 + 15*160 = 7 AF 16 = 0 x 07 AF = H‘ 07 AF n 4 Zeichen einer Binärzahl lassen sich durch eine Hexadezimal-ziffer darstellen (4 Binärziffern nennt man auch NIBBLE) n Oktalsystem n Zeichen: 0, 1, 2, 3, 4, 5, 6, 7 n 199910 = 3*83 + 7*82 + 1*81 + 7*80 = 37178 n 3 Zeichen einer Binärzahl lassen sich durch eine Oktalziffer darstellen

3. 2. 2 Konvertierung: „Intuitivmethode“ n Addition von geigneten Zweierpotenzen (Dezimalzahl Dualzahl) n positive Zweierpotenzen für Vorkommaanteil n negative Zweierpotenzen für Nachkommaanteil n Vorgehen (getrennt nach Vor- und Nachkommateil) n Suche größte Zweierpotenz, die noch in die Zahl passt n Subtrahiere die Zweipotenz von der Zahl daraus ergibt sich die neue Zahl für die Suche der Zweierpotenz n Dieses Vorgehen terminiert. . . l. . . beim Vorkommateil: wenn die Zahl = 0 l. . . beim Nachkommateil: wenn die Zahl erreicht ist, vielleicht nie n Beispiel: 39 7 3 1 100111 25 39 - 32 22 7 -4 21 3 -2 20 1 -1 =7 =3 =1 =0 0, 8125 0, 3125 0, 0625 0, 1101 2 -1 0, 8125 - 0, 5 = 0, 3125 2 -2 0, 3125 - 0, 25 = 0, 0625 2 -4 0, 0625 - 0, 0625 = 0

3. 2. 2 Konvertierung: Restwertmethode n Erzeugen des Hornerschemas (Ausklammern der Basis b) c 0 = anbn + an-1 bn-1 +. . . + a 2 b 2 +a 1 b 1 + a 0 b 0 c 0 = ((. . . (anb + an-1) b +. . . + a 2) b +a 1) b + a 0 c 0 / b = c 1 Rest a 0 , mit c 0= (. . . (anb + an-1) b +. . . + a 2) b +a 1 , c 1 / b = c 2 Rest a 1 , mit c 1=. . . (anb + an-1) b +. . . + a 2 , . . . cn / b = 0 Rest an ( terminiert mit cn+1 = 0 ) n Konversion der Nachkommastellen (folgt aus Hornerschema): 1. Multiplikation mit Basis (bis ganzzahliges Ergebnis oder gewünschte Genauigkeit) 2. Abspalten der Vorkommastelle des Ergebnisses, weiter mit 1. 19 : 2 = 9 Rest 1 0, 6875 * 2 = 1, 375 1 abspalten n Beispiel 9 : 2 = 4 Rest 1 0, 375 * 2 = 0, 75 0 abspalten 4 : 2 = 2 Rest 0 0, 75 * 2 = 1, 5 1 abspalten 2 : 2 = 1 Rest 0 0, 5 * 2 = 1 1 abspalten 1 : 2 = 0 Rest 1 0, 1011 11001

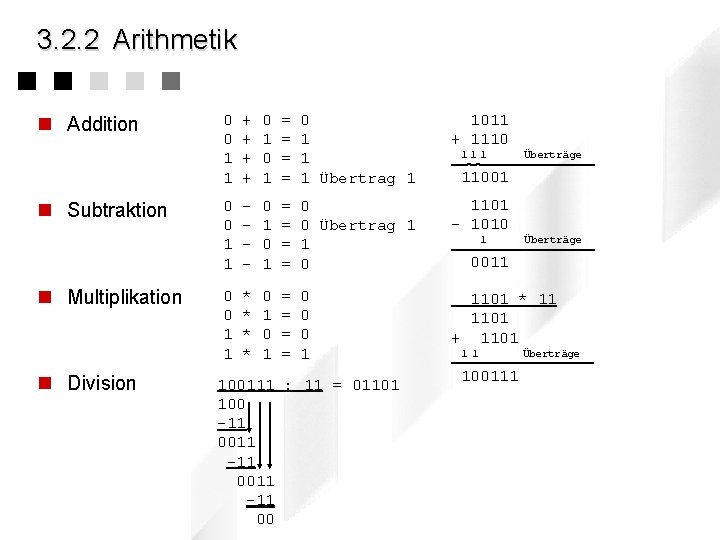
3. 2. 2 Arithmetik n Addition n Subtraktion n Multiplikation n Division 0 0 1 1 + + 0 1 = = 0 1 1 1 Übertrag 1 1011 + 1110 0 0 1 1 - 0 1 = = 0 0 Übertrag 1 1 0 1101 - 1010 0 0 1 1 * * 0 1 = = 0 0 0 1 1101 * 11 1101 + 1101 100111 : 11 = 01101 100 -11 0011 -11 00 111 Überträge 11001 1 Überträge 0011 1 1 100111 Überträge

3. 2. 3 Ganze positive Zahlen n Positive ganze Zahlen werden meist direkt in ihrer binären Darstellung kodiert. n Die BCD (Binäry Coded Digits) - Darstellung von Zahlen ist eine Mischform aus Dezimal- und Binärdarstellung: 0 0000 n n Jede Ziffer der Dezimalzahl wird binär dargestellt. Die Darstellung jeder Ziffer erfolgt mit 4 Bits. Die Reihenfolge der Ziffern bleibt erhalten. Beispiele: l l 7 0111 53 0101 0011 1234 0001 0010 0011 0100 1999 0001 1001 1 2 3 4 5 6 7 8 9 Pseudotetraden 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

3. 2. 4 Ganze negative Zahlen: Probleme n Darstellung des Vorzeichens im ersten Bit, z. B. 0000 0001 0010 0011 0100 0101 0110 0111 = = = = 0 1 2 3 4 5 6 7 1000 1001 1010 1011 1100 1101 1110 1111 = = = = 0 -1 -2 -3 -4 -5 -6 -7 n Nachteil durch Redundanz der Darstellung der 0 n Nachteil durch Probleme beim formalen Addieren 1011 + 0001 1100 -3 +1 -4

3. 2. 4 Ganze negative Zahlen: Zweierkomplement n Zweierkomplementdarstellung -2 n. . . +(2 n-1) n Negative Zahl durch bitweise Komplementierung und Addition von 1. n 0000 = 0 1000 = -8 Beispiel: 3 0001 = 1 1001 = -7 0011 Binärdarstellung 0010 = 2 1010 = -6 1100 Komplement 0011 = 3 1011 = -5 1101 Komplement + 1 = -3 0100 = 4 1100 = -4 0101 = 5 1101 = -3 0110 = 6 1110 = -2 0111 = 7 1111 = -1 n Vorteile l Darstellung des Vorzeichens im ersten Bit l Abdeckung von 16 Zahlen, also keine Redundanz l Kein Nachteil durch Probleme beim formalen Addieren n Subtraktion durch Addition des Zweierkomplements (Überlauf weglassen) -3 1101 +1 +0001 -1 1111 -1 +1111

3. 2. 5 Gebrochene Zahlen: Binärdarstellung n Darstellung mit Vor- und Nachkommateil n Beispiele Gebrochene Binärzahl Gebrochene Dezimalzahl 0. 1 0, 5 0. 01 0, 25 111 7, 875 0. 0001 1001. . 0, 1 n Mit 32 Bit lassen sich nur 232 verschiedene Zahlen darstellen. n Problem: extrem große und extrem kleine Zahlen lassen sich mit wenigen Bits nicht darstellen n Bei 8 Bit mit 4 Vorkomma und 4 Nachkommastellen (ohne Vorzeichen): 0000. 0001 < n < 1111 0, 0675 < n < 15, 9425

3. 2. 5 Gebrochene Zahlen: Exponentialdarstellung n Anforderung n sehr große und sehr kleine Zahlen sollen darstellbar sein l Masse Elektron = 9 * 10 -28 g l Anzahl Moleküle pro Mol = 6, 022 * 1023 n die relativen Genauigkeiten sind wichtiger als die absoluten l Ältere Quellen geben die Anzahl der Moleküle pro Mol mit 6, 065 * 1023 an l Eine Änderung in der Mantisse von 0, 04 entspricht einer Toleranz von 6, 065 / 6, 022 1, 0071 also ca. 0, 7%. n Fixkommadarstellung wäre große Verschwendung n zur Darstellung dieser beiden Größen wären 194 Bit nötig l 87 Bit Vorkommateil l 107 Bit Nachkommateil n Idee: Signifikante Stellen und Größenordnung werden getrennt n Signifikant Masse Elektron: 9 n Größenordnung Masse Elektron: 10 -28

3. 2. 5 Gleitpunktzahlen: Real Darstellung n Darstellung durch Real-Zahlen, bestehend aus drei Teilen: n Vorzeichenbit V Gibt an, ob die Zahl positiv oder negativ ist n Mantisse M Wird mit dem Exponenten multipliziert l Die Normalform wird erreicht, indem das Komma soweit nach links oder rechts geschoben wird, bis die erste Stelle nach dem Dezimalpunkt die erste von Null verschieden Ziffer ist. Der Exponent wird entsprechend der Verschiebungen erhöht oder vermindert. n Exponent E Potenz einer Basiszahl (2) mit der die Mantisse multipliziert wird l wird oft in „BIAS“-Darstellung abgelegt, d. h. wird mit 126 addiert um negatives Vorzeichen zu vermeiden. l Vorsicht: 126 (nicht 128). Asymmetrisch, da 21 bei der Normalisierung zweimal geschoben wird, 2 -1 gar nicht

3. 2. 5 Gleitpunktzahlen: Umwandlung n Umwandlung Dezimalzahl in binäre Gleitpunktzahl (nach IEEE 754) 1. Umwandlung der Dezimalzahl in Binärzahl mit Nachkommateil 2. Verschieben des Kommas nach links oder rechts bis zur Normalform 1. Damit ist erste Nachkommastelle = 1 und daher redundant, kann also in der Mantisse weggelassen werden. 2 * größere Genauigkeit der Mantisse 3. Addition des BIAS =126 (um negative Exponenten zu vermeiden) Umwandlung in binäre Form 4. Das Vorzeichen der Mantisse wird bestimmt: positiv 0, negativ 1 5. IEEE 754 sieht noch eine optionale Rundung der Mantisse vor n Nicht jede gebrochene Dezimalzahl lässt sich endlich als gebrochene Binärzahl darstellen (und umgekehrt). n Dadurch entstehen Rundungsfehler

3. 2. 5 Gleitpunktzahlen: Beispiele n Beispiel: 148, 62510 1. Konvertieren: 2. Normalisieren: M 10010100, 101 = 0, 100101*2+8 Exponent ist 8. = 00101 (die führende 1 ist in Normalform redundant) 3. Bias addieren E = 12610 + 810 = 13410 = 100001102 4. Vorzeichen V = 0 5. Ergebnis: VEEEEMMMMMMMMMMMM 010000110001010000000 n Beispiel: -2, 7510 1. Konvertieren: 2. Normalisieren: M 10, 11 = 0, 1011*2+2 Exponent ist 2. = 011 (die führende 1 ist in Normalform redundant) 3. Bias addieren E = 12610 + 210 = 12810 = 100000002 4. Vorzeichen V = 1 5. Ergebnis: VEEEEMMMMMMMMMMMM 1100000000000000

3. 2. 5 Gleitpunktzahlen: Arithmetik n Addition/Subtraktion n Die Exponenten werden angeglichen, indem die Mantisse des Operanten mit dem kleineren Absolutbetrag entsprechend verschoben wird. n Anschließend werden die Mantissen addirt n Beim Verschieben können Stellen verloren gehen. n Multiplikation n Die Mantissen der Operanten werden multipliziert n Die Exponenten werden addiert n Sind die Exponenten zu groß, kann es zu Exponenten-Overflow kommen n Division n Die Mantissen der Operanten werden dividiert n Der Exponent ergibt sich aus der Differenz des Dividenden und Divisors n Ist der Divisor zu klein und/oder Dividend zu groß kann es zu einem Exponenten-Underflow kommen. Das Ergebnis wird dann zu 0, alle Ziffern sind verloren n Nach allen Operationen wird die Normalform ggf. wiederhergestellt

3. 2. 6 Standards n n n Short -128. . . 127 (8 Bit) Integer -32768. . . 32767 (16 Bit) Unsigned Int 0. . . 65535 (16 Bit) Long. Int -2147483648. . . 2147483648 (32 Bit) Real nach IEEE 754 n n Float 1 VZ-Bit, 8 Bit E, 23 Bit M (32 Bit) Double 1 VZ-Bit, 11 Bit E, 52 Bit M (64 Bit) zwei Varianten 0, 5 M < 1 bzw. 1 M < 2 spezielle Werte für Na. N (not a number) und infinity

3. 3 Zusammenfassung des Kapitels n Kodierung von Zeichen n ASCII n EBCDIC n UNICODE n Darstellung von Zahlen n n n n Zahlensysteme Konvertierung Arithmetik Ganze positive Zahlen Ganze negative Zahlen Gebrochene Zahlen Gleitpunktzahlen Standards

Übung 3. 1 1. Die Duodezimalindianer haben zwölf Finger 1. Berechnen Sie nach dem Zahlensystem der Duodezimalindianer die wichtigsten Werte des täglichen Lebens: 1. 300 g Pizza 2. Eine Flasche Bier (0, 5 bzw. 0, 33 Liter) 3. ALDI 2. 95 € 2. Konvertieren Sie die obigen Werte auch in Bin, Hex und Okt 2. Grundrechenarten (verwenden Sie keinen Rechner) 1. 2. 3. 4. Berechnen Sie 568210 / 1910 Konvertieren Sie 568210 und 1910 ins Binärsystem Dividieren Sie die Binärdarstellungen der beiden Zahlen Machen Sie die Gegenprobe im Binärsystem 3. Konvertieren Sie 0, 110 ins Binärsystem 4. Was bedeutet: 44 65 72 20 42 61 6 C 6 C 20 69 73 74 20 72 75 6 E 64 2 E

Übung 3. 2 1. Konvertieren Sie 0, 1 mit der Restwertmethode 2. Addieren Sie paarweise alle Zahlen von -3 bis +4 (also 28 Additionen), verwenden Sie dabei die Darstellung negativer Zahlen im Zweierkomplement. 3. (optional) Programmieren Sie in PHP 4/HTML-Forms einen Konverter zur Konvertierung ganzer und gebrochener Zahlen zwischen beliebigen Zahlensystem und zur Darstellung im IEEE 754 float und double Format. 4. Stellen Sie 1. als IEEE 754 float-Zahl dar 2. als IEEE 754 double-Zahl dar 5. Geben Sie im Binärsystem und Dezimalsystem 1. den größt- bzw. kleinst-möglichen Wert einer float-Zahl an 2. den größt- bzw. kleinst-möglichen Wert einer double-Zahl an