Intro to Theory of Computation LECTURE 3 Last

Intro to Theory of Computation LECTURE 3 Last time: • DFAs and NFAs • Operations on languages Today: • Nondeterminism • Equivalence of NFAs and DFAs • Closure properties of regular languages Sofya Raskhodnikova 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 1

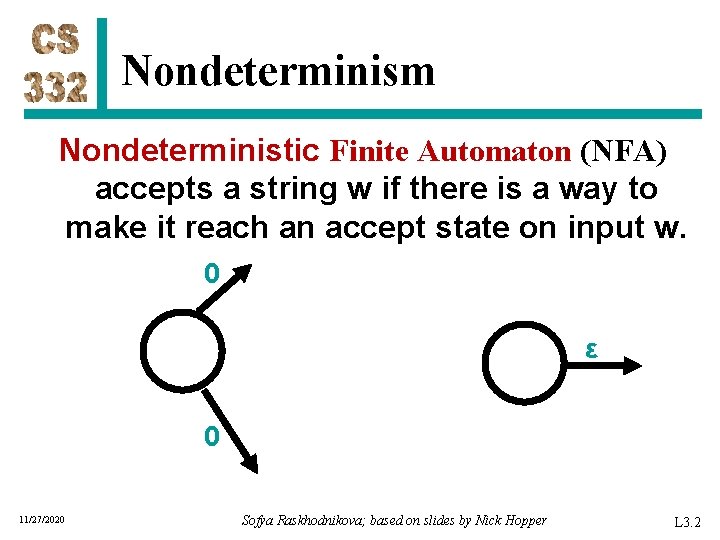
Nondeterminism Nondeterministic Finite Automaton (NFA) accepts a string w if there is a way to make it reach an accept state on input w. 0 ε 0 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 2

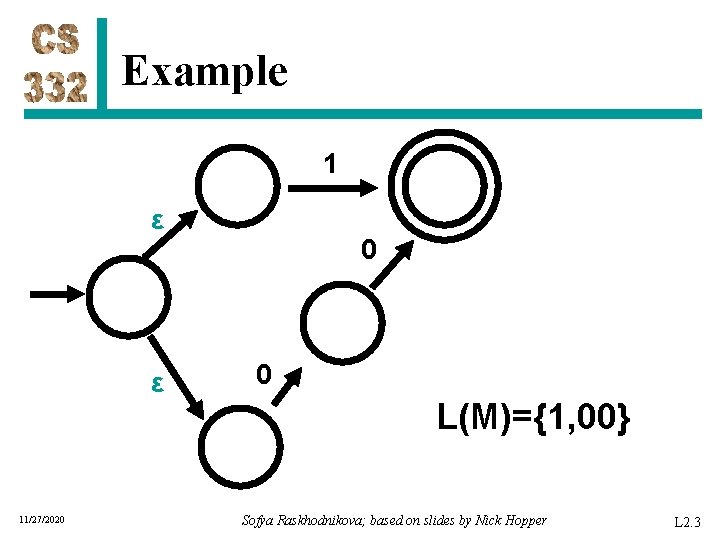
Example 1 ε ε 11/27/2020 0 0 L(M)={1, 00} Sofya Raskhodnikova; based on slides by Nick Hopper L 2. 3

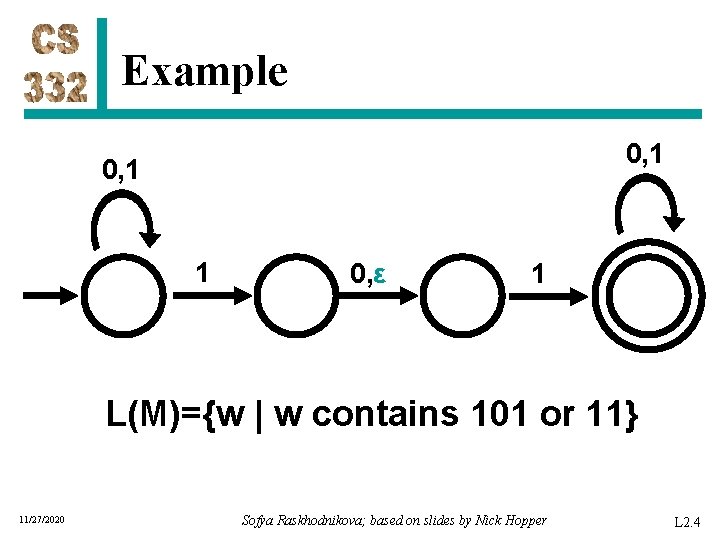
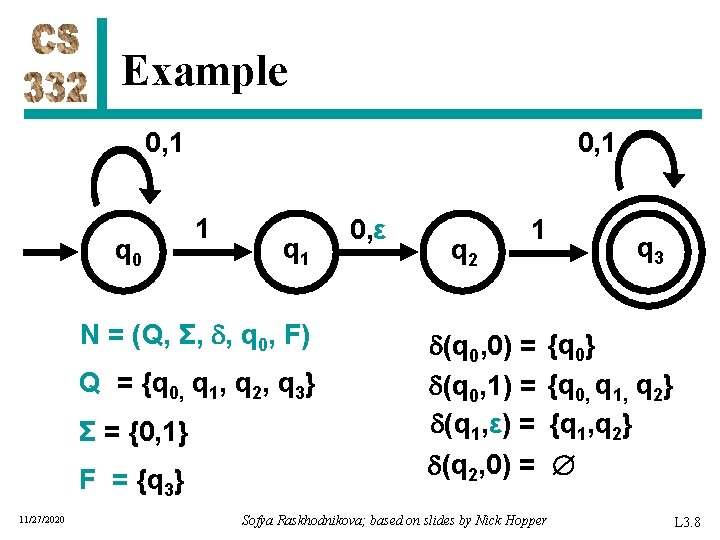
Example 0, 1 1 0, ε 1 L(M)={w | w contains 101 or 11} 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 2. 4

Exercise • 0 ε ε 0 0

Formal Definition • An NFA is a 5 -tuple M = (Q, Σ, , q 0, F) Q is the set of states Σ is the alphabet : Q Σε → P(Q) is the transition function q 0 Q is the start state F Q is the set of accept states • Σε = Σ {ε} and P(Q) is the set of subsets of Q • M accepts a string w if there is a path from q 0 to an accept state that w follows. 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 6

Example 0, 1 q 0 0, 1 1 q 1 N = (Q, Σ, , q 0, F) Q = {q 0, q 1, q 2, q 3} Σ = {0, 1} F = {q 3} 11/27/2020 0, ε q 2 1 (q 0, 0) = (q 0, 1) = (q 1, ε) = (q 2, 0) = q 3 {q 0} {q 0, q 1, q 2} {q 1, q 2} Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 8

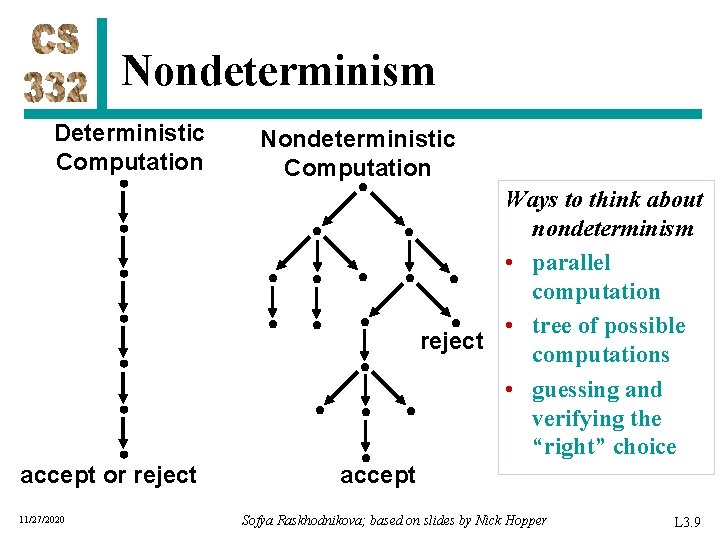
Nondeterminism Deterministic Computation Nondeterministic Computation Ways to think about nondeterminism • parallel computation • tree of possible reject computations • guessing and verifying the “right” choice accept or reject 11/27/2020 accept Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 9

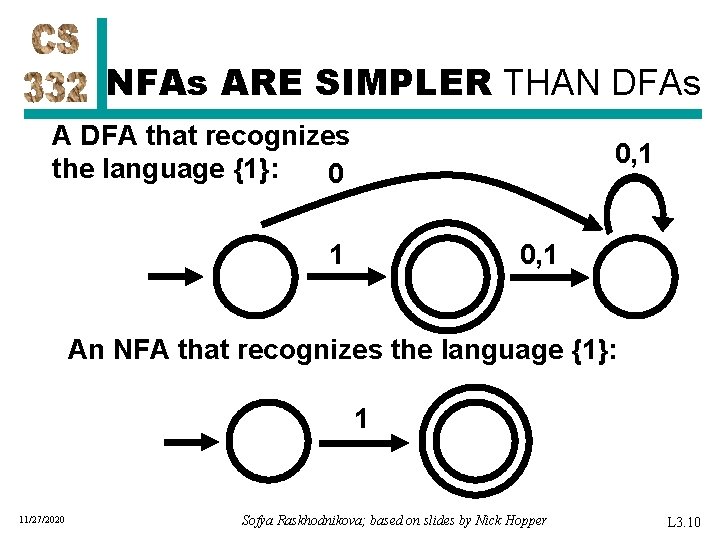
NFAs ARE SIMPLER THAN DFAs A DFA that recognizes the language {1}: 0 0, 1 1 0, 1 An NFA that recognizes the language {1}: 1 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 10

A DFA recognizing {1} Theorem. Every DFA for language {1} must have at least 3 states. Proof: 11/27/2020 L 3. 11

Equivalence of NFAs & DFAs Theorem. Every NFA has an equivalent DFA. Corollary: A language is regular iff it is recognized by an NFA. 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 12

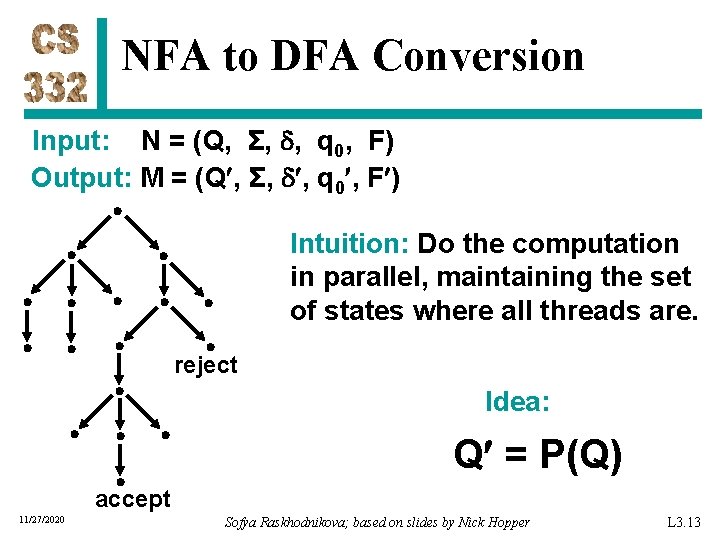
NFA to DFA Conversion Input: N = (Q, Σ, , q 0, F) Output: M = (Q , Σ, , q 0 , F ) Intuition: Do the computation in parallel, maintaining the set of states where all threads are. reject Idea: Q = P(Q) accept 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 13

NFA to DFA Conversion Input: N = (Q, Σ, , q 0, F) Output: M = (Q , Σ, , q 0 , F ) Q = P(Q) : Q Σ → Q q 0 = F = { R Q | R contains some accept state of N} 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 14

Example: NFA to DFA 1) 11/27/2020 a 1 b Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 15

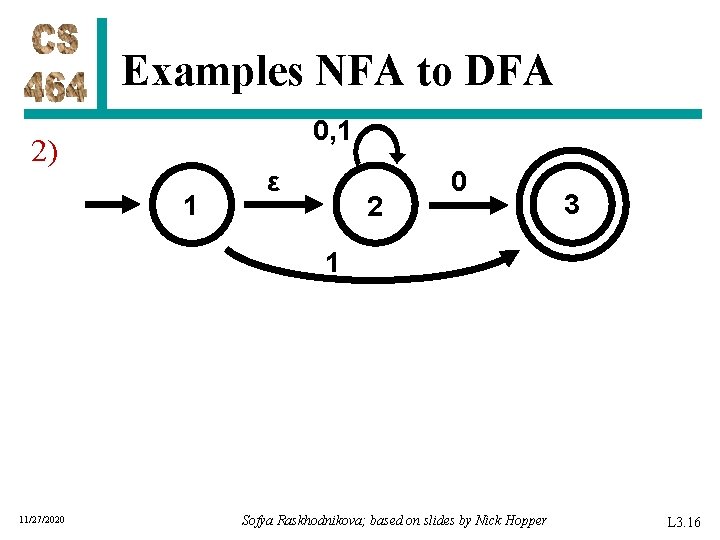
Examples NFA to DFA 0, 1 2) 1 ε 2 0 3 1 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 16

NFA to DFA Conversion Input: N = (Q, Σ, , q 0, F) Output: M = (Q , Σ, , q 0 , F ) Q = P(Q) : Q Σ → Q r R q 0 = E({q 0}) F = { R Q | R contains some accept state of N} 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 17

Regular Operations on languages Complement: A = { w | w A } Union: A B = { w | w A or w B } Intersection: A B = { w | w A and w B } Reverse: AR = { w 1 …wk | wk …w 1 A } Concatenation: A B = { vw | v A and w B } Star: A* = { w 1 …wk | k ≥ 0 and each wi A } 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 18

Closure properties of the class of regular languages THEOREM. The class of regular languages is closed under all 6 operations. If A and B are regular, applying any of these operation yields a regular language. 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 19

Palindromes A palindrome is a word or a phrase that reads the same forward and backward. Examples • mom • madam • Never odd or even. • Stressed? No tips? Spit on desserts! 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 20

Exercise •

Closure under reverse Theorem. The reverse of a regular language is also regular • ε 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper ε ε L 3. 22

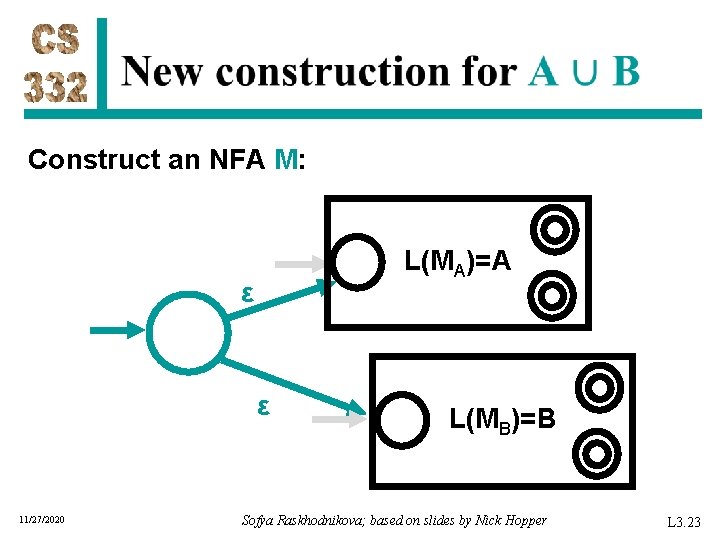
Construct an NFA M: L(MA)=A ε ε 11/27/2020 L(MB)=B Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 23

Concatenation operation Concatenation: A B = { vw | v A and w B } Theorem. If A and B are regular, A B is also regular. Proof: Given DFAs M 1 and M 2, construct NFA by connecting all accept states in M 1 to the start state in M 2. ε L(M 1)=A L(M 2)=B ε 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 24

Concatenation operation Concatenation: A B = { vw | v A and w B } Theorem. If A and B are regular, A B is also regular. Proof: Given DFAs M 1 and M 2, construct NFA by connecting all accept states in M 1 to the start state in M 2. • Make all states in M 1 non-accepting. ε L(M 1)=A L(M 2)=B ε 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 25

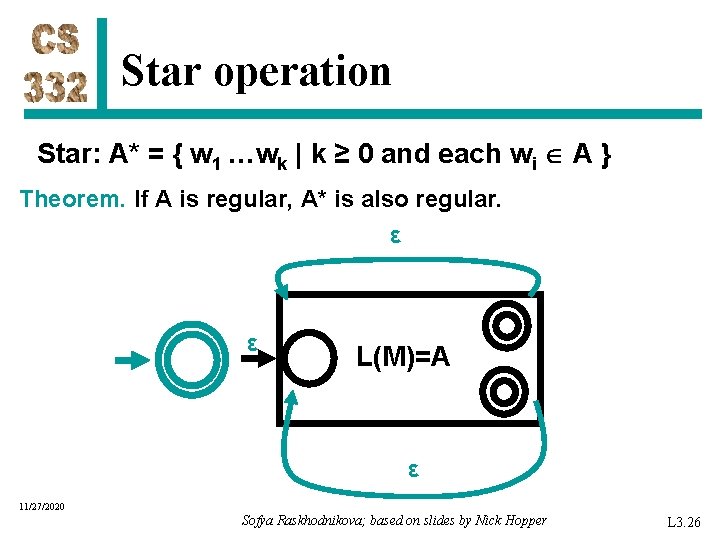
Star operation Star: A* = { w 1 …wk | k ≥ 0 and each wi A } Theorem. If A is regular, A* is also regular. ε ε L(M)=A ε 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 26

The class of regular languages is closed under Regular operations Union: A B = { w | w A or w B } Concatenation: A B = { vw | v A and w B } Star: A* = { w 1 …wk | k ≥ 0 and each wi A } Other operations Complement: A = { w | w A } Intersection: A B = { w | w A and w B } Reverse: AR = { w 1 …wk | wk …w 1 A } 11/27/2020 Sofya Raskhodnikova; based on slides by Nick Hopper L 3. 27