Intro to Computation AI Dr Jill Fain Lehman

Intro to Computation & AI Dr. Jill Fain Lehman School of Computer Science Lecture 5: November 20, 1997

Review • Introduced graph structures & basic operations • Homework: think about knowledge and knowledge-rich processes – During generation (e. g. similar sites) – During traversal (e. g. query search) • Today: 2 examples of how AI uses graphs – Semantic nets & inheritance – Constraint satisfaction

Semantic Nets • Type of slot-and-filler structure. • Meaning of concept comes from way it is connected to other objects. • Graph nodes represent objects; labeled edges represent relations between objects or attributes and their values. • Edge labels may be domain independent or domain dependent. • Edge types usually play a role in processing. Main process: inheritance.

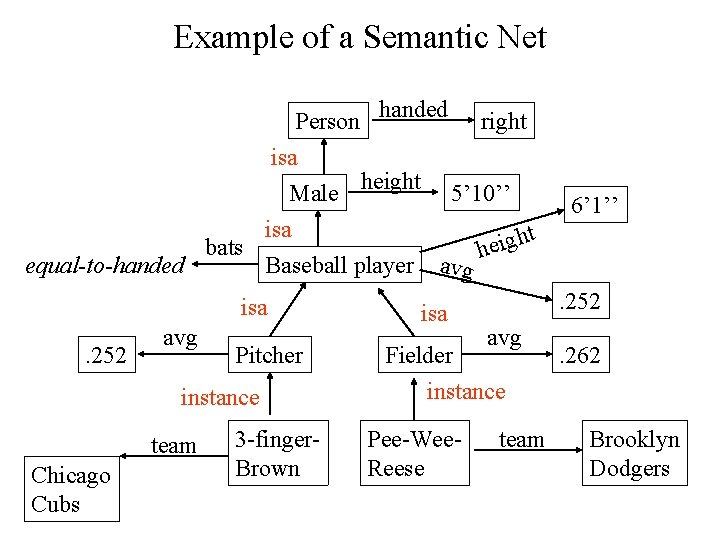
Example of a Semantic Net Person handed equal-to-handed bats isa Male height isa Baseball player isa. 252 avg Pitcher instance team Chicago Cubs 3 -finger. Brown right 5’ 10’’ 6’ 1’’ t avg isa h heig . 252 avg Fielder instance Pee-Wee. Reese team . 262 Brooklyn Dodgers

Attributes & Values • Isa and instance: class inclusion and membership. More generally an attribute A may be a specialization or generalization of another attribute, e. g. height/physical-size. • Inverses, e. g. has-part/part-of. • Semantics of attribute may restrict value, e. g. average must be a number between. 000 and 1. 000. , age of a person < age of each parent. • Values may be given, computed or inherited.

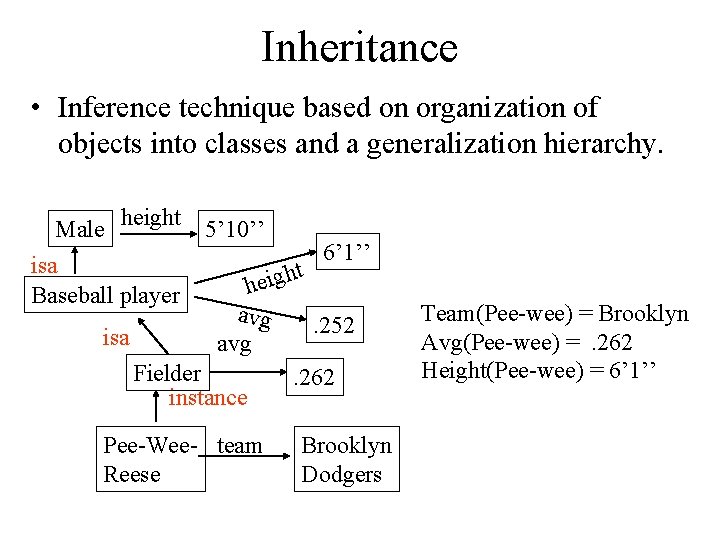
Inheritance • Inference technique based on organization of objects into classes and a generalization hierarchy. Male height 5’ 10’’ isa Baseball player 6’ 1’’ ht g i e h avg. 252 isa avg Fielder. 262 instance Pee-Wee- team Reese Brooklyn Dodgers Team(Pee-wee) = Brooklyn Avg(Pee-wee) =. 262 Height(Pee-wee) = 6’ 1’’

Inheritance Algorithm To retrieve a value V for attribute A of an instance object O: 1. Find O in the net. 2. If there is a value there for A report that value. 3. Otherwise follow the instance link (no link means failure) and report the value of A associated with the class. 4. Otherwise follow isa links up the hierarchy until a value V is found for A or until no more isa links are available. Fine if your hierarchy is a tree…but what if it’s a directed, acyclic graph (DAG)?

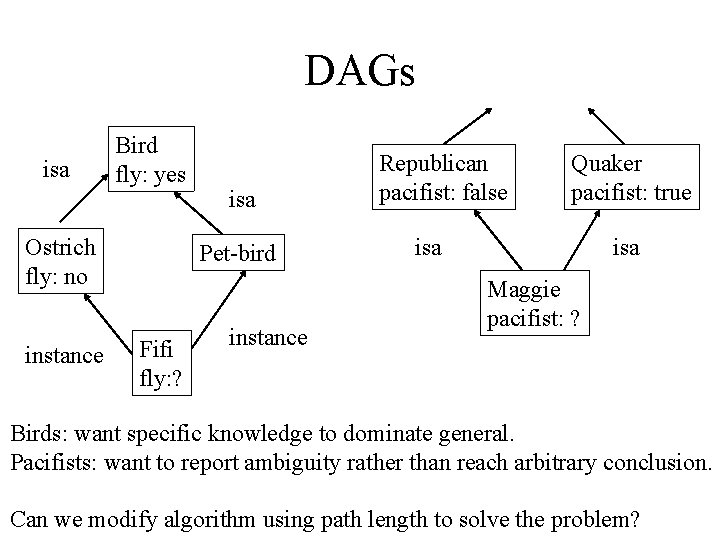
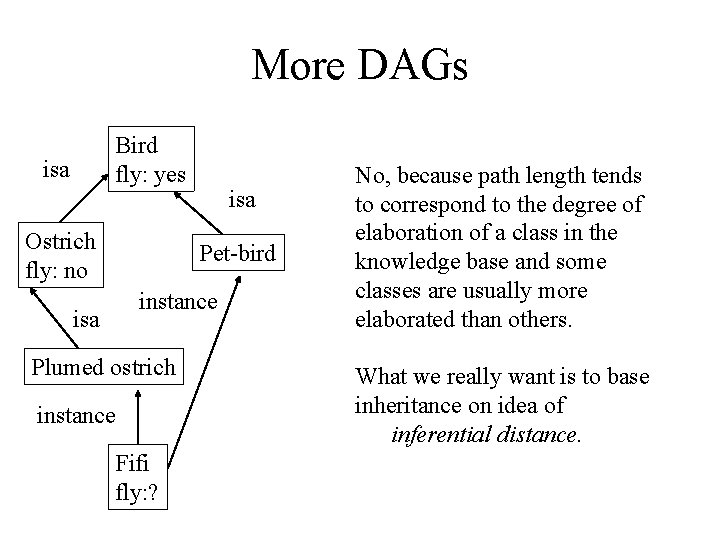
DAGs isa Bird fly: yes Ostrich fly: no instance isa Pet-bird Fifi fly: ? instance Republican pacifist: false Quaker pacifist: true isa Maggie pacifist: ? Birds: want specific knowledge to dominate general. Pacifists: want to report ambiguity rather than reach arbitrary conclusion. Can we modify algorithm using path length to solve the problem?

More DAGs Bird fly: yes isa Ostrich fly: no isa Pet-bird instance isa Plumed ostrich instance Fifi fly: ? No, because path length tends to correspond to the degree of elaboration of a class in the knowledge base and some classes are usually more elaborated than others. What we really want is to base inheritance on idea of inferential distance.

Inferential Distance (Touretzky) • Class 1 is closer to class 2 than to class 3 iff class 1 has an inference path through class 2 to class 3. • Note: defines only a partial ordering. • Inheritance for feature f gives the set of competing values such that each value v – Has been derived from a class c in f’s class hierarchy and – v is not contradicted by any class that has a shorter inferential distance to c than f does.

Semantic Nets: Conclusions • In general, anything you can do in a predicate logic theorem prover you can do in a semantic net via inheritance. • Semantic nets can be boosted to first-order logic through the use of partitioning. • Frame languages (e. g. Parmenides) formalize nets and their operations; they are programming languages based on the architecture of nets. • A net involves representational decisions that affect completeness and correctness: the paradigm is general, the power comes from the content.

Constraint Satisfaction • Many problems viewed as choosing consistent assignment of values to features, e. g. : speech & NL, vision, job-shop scheduling/logistics. • Number of values/feature may be large, number of combinations of feature/value intractable. • But not all feature/values and combinations may be permissible. – Naturally-occurring constraints – Imposed constraints (e. g. homework) • Use constraint knowledge to cut down search.

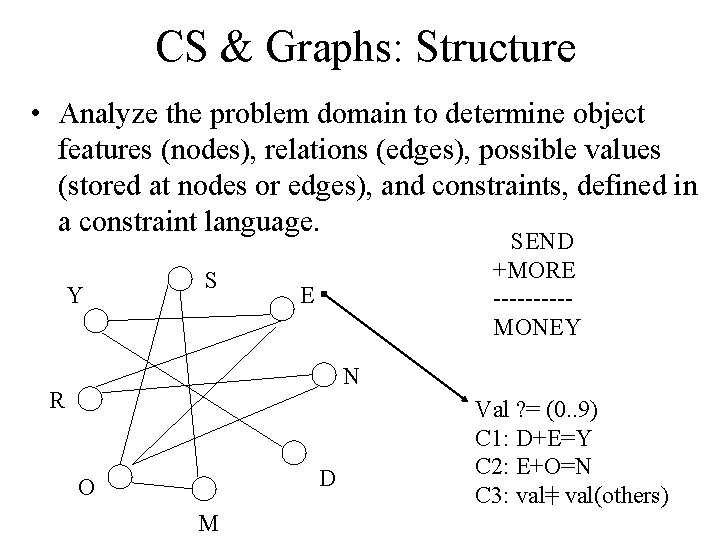
CS & Graphs: Structure • Analyze the problem domain to determine object features (nodes), relations (edges), possible values (stored at nodes or edges), and constraints, defined in a constraint language. Y S SEND +MORE -----MONEY E N R D O M Val ? = (0. . 9) C 1: D+E=Y C 2: E+O=N C 3: val= val(others)

CS & Graphs: Operations • Constraints are propagated along edges that relate dependent objects, generally until each feature is assigned a single value. • Search may be required to propagate hypothetical constraints (guesses at values); these constraints will need to be undone when they lead to inconsistencies (the inability to assign some other feature a value given the guess).

Domain-independent CS Algorithm 1. Set OPEN to the set of vertices. Then do until an inconsistency is detected or until OPEN is empty: a. Select an OBJ in OPEN and reduce possible values according to constraints provided by adjacency set. b. If first time OBJ examined or if values reduced, add adjacency set to OPEN. c. Remove OBJ from OPEN. 2. If each feature has a single value then quit (solution found). 3. If inconsistency arose, return failure. 4. If neither 2 nor 3 then until solution is found or all solutions have been eliminated: a. Select an object whose value is not determined and assign a value. b. Recursively invoke CS on graph.

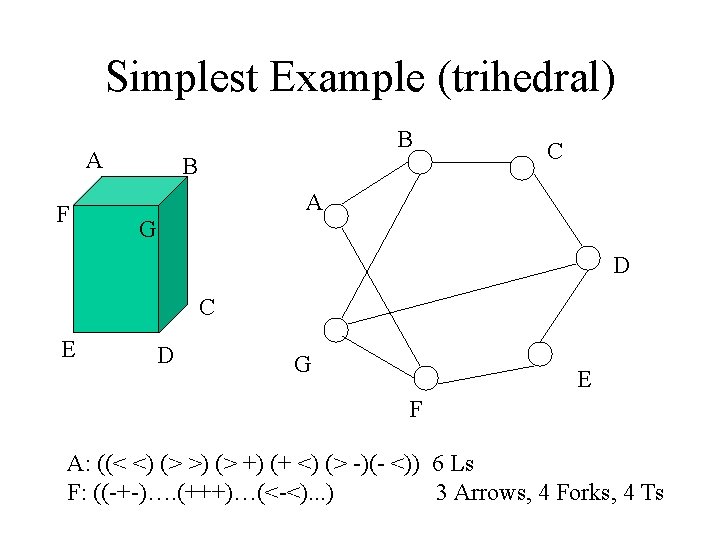
Example: Scene Analysis for Polyhedra

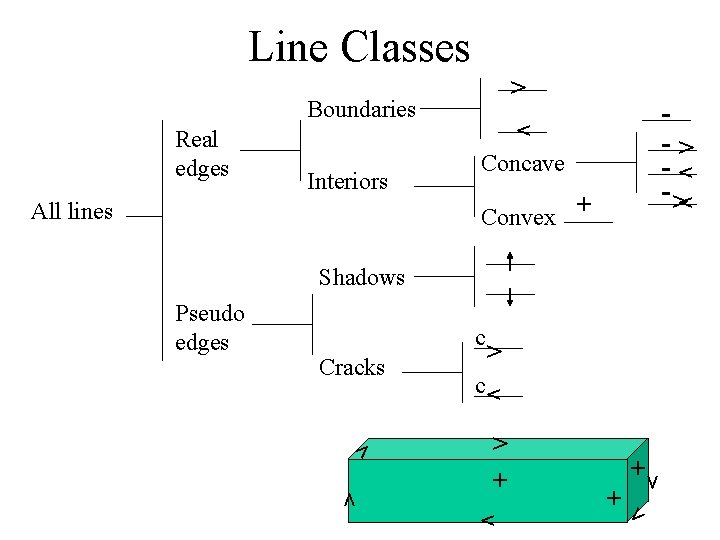
Line Classes > Boundaries All lines Concave > > Interiors > Real edges -> -> Convex + Shadows > + + + > > > c > > Cracks > c > Pseudo edges

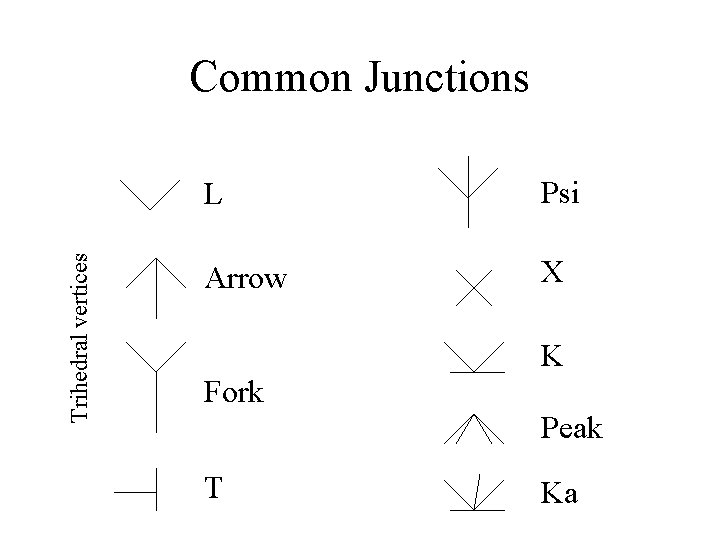
Trihedral vertices Common Junctions L Psi Arrow X K Fork Peak T Ka

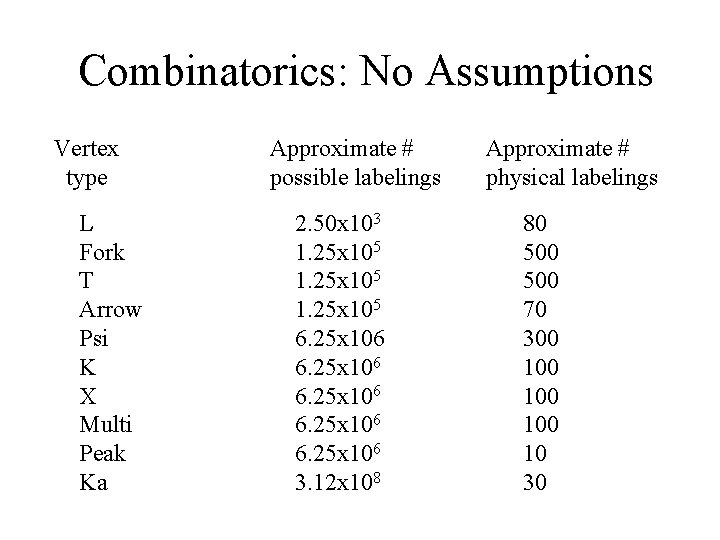
Combinatorics: Simple Case • Trihedral vertices, no concave or crack edges, uniform illumination (no shadows) – 4 ways to label a line, so • 42 = 16 labelings for an L • 43 = 64 labelings fork, arrow, and T • BUT out of 208 junctions, only 18 are physically possible • Still, savings don’t look that big. . .

Combinatorics: No Assumptions Vertex type L Fork T Arrow Psi K X Multi Peak Ka Approximate # possible labelings 2. 50 x 103 1. 25 x 105 6. 25 x 106 3. 12 x 108 Approximate # physical labelings 80 500 70 300 100 10 30

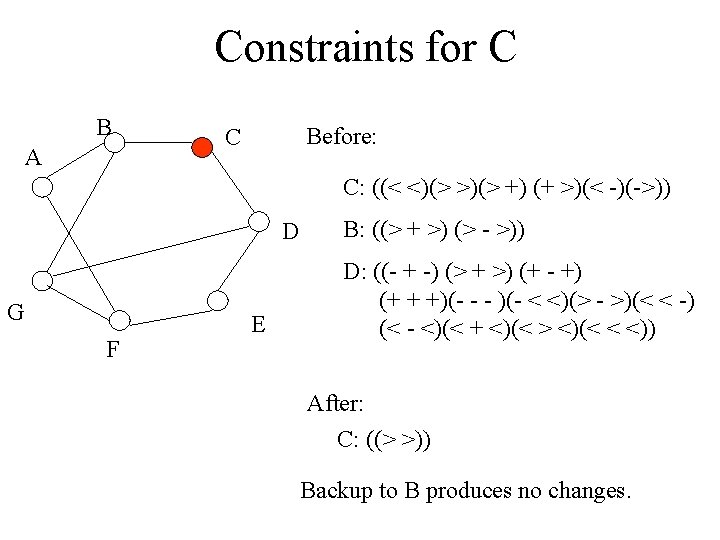
Waltz’s Algorithm 1. Find borders and label them: border has no vertices outside it. 2. Number vertices to be traversed in order: a. Number boundary vertices first. b. Number interior vertices by moving from a numbered vertex toward an adjacent unnumbered one. 3. Now visit each vertex V in order and attempt to label: a. Attach all physically possible labels of type V. b. For each vertex A adjacent to V and already visited, eliminate from V any labeling for which there is no consistent label at A. c. For each vertex adjacent to A visited in step b, do: i. Eliminate labels inconsistent with V. ii. If any eliminated, propagate constraints to neighbors of A. iii. Continue to propagate until there are no adjacent labeled vertices or no change made to a set.

Simplest Example (trihedral) B A F B C A G D C E D G E F A: ((< <) (> >) (> +) (+ <) (> -)(- <)) 6 Ls F: ((-+-)…. (+++)…(<-<). . . ) 3 Arrows, 4 Forks, 4 Ts

Waltz’s Algorithm Factoids • Guaranteed to find unique correct figure labeling if one exists. • If more than one labeling exists, at least one vertex set will have multiple entries; by doing a depth-first exhaustive traversal of the graph you can generate all possible labelings. • Illumination serves to reduce ambiguity.

Constraint Satisfaction: Conclusions • Constraints are a source of knowledge that can be traded off against search. • The expressive power of the constraint language trades off against the cost of propagating constraints and detecting inconsistencies. • In general, strong constraints may make an intractable problem computable in practice, but does not change the basic exponential nature of the search space.