Inteligencia Artificial Lgica difusa Primavera 2009 profesor Luigi

Inteligencia Artificial Lógica difusa Primavera 2009 profesor: Luigi Ceccaroni

El modelo posibilista • El modelo posibilista (o teoría de la posibilidad) está basado en los conjuntos difusos de Zadeh (1965). • El objetivo es modelar los grados de veracidad, la imprecisión o la vaguedad contenidas en proposiciones como: – La temperatura es alta. – Hay que girar un poco a la derecha. – Es muy seguro que tenga hepatitis. – La hipótesis H 1 es muy poco posible. 2

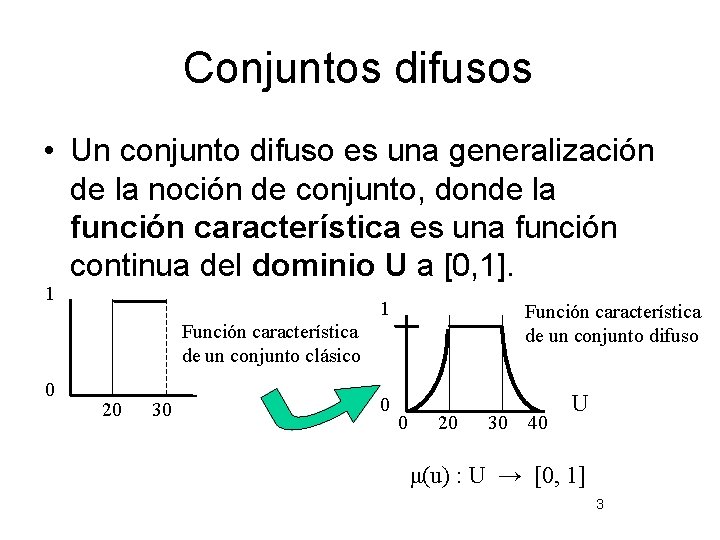
Conjuntos difusos • Un conjunto difuso es una generalización de la noción de conjunto, donde la función característica es una función continua del dominio U a [0, 1]. 1 1 Función característica de un conjunto difuso Función característica de un conjunto clásico 0 20 30 0 0 20 30 40 U μ(u) : U → [0, 1] 3

Función característica • La función característica (πA) indica la posibilidad de que un valor u, u∈U, compatible con la variable X, sea A, sabiendo que [X es A] corresponde al grado de pertenencia en el conjunto difuso representado por la etiqueta A. 4

Posibilidad y grado de veracidad • Cada variable tiene un dominio (U). • Se usan etiquetas lingüísticas para representar una distribución de posibilidad sobre estos valores. • Dependiendo de la distribución de posibilidad, cada valor de la variable es, respecto a la etiqueta: – cierto – imposible (falso) – posible hasta cierto punto 5

Posibilidad y grado de veracidad • Los hechos difusos se representan siguiendo el esquema: [X es A] que define un conjunto difuso sobre U donde: – X es una variable sobre el dominio U. – A es un término lingüístico aplicable a X que restringe sus valores. 6

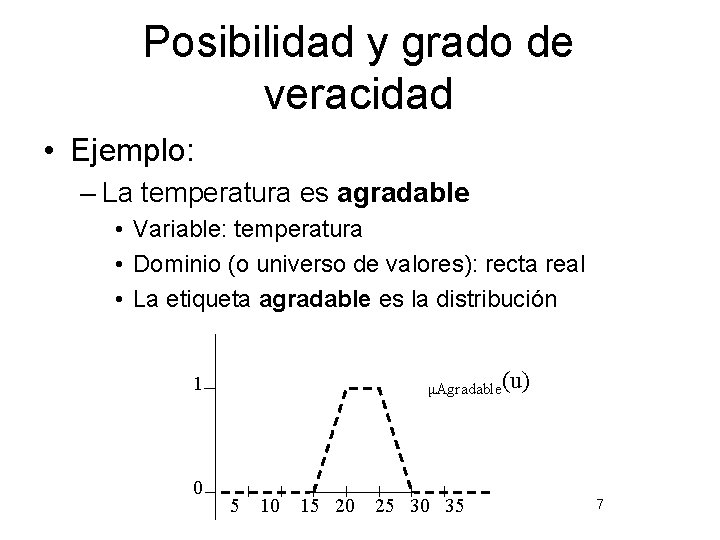
Posibilidad y grado de veracidad • Ejemplo: – La temperatura es agradable • Variable: temperatura • Dominio (o universo de valores): recta real • La etiqueta agradable es la distribución μAgradable(u) 1 0 5 10 15 20 25 30 35 7

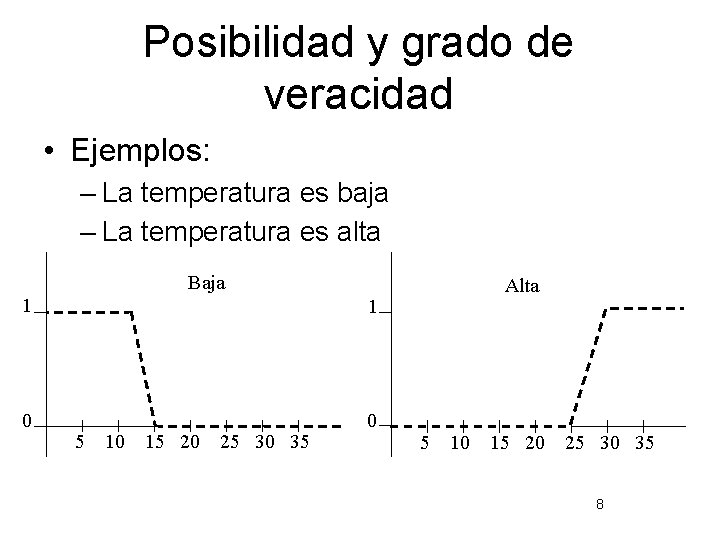
Posibilidad y grado de veracidad • Ejemplos: – La temperatura es baja – La temperatura es alta Baja 1 1 0 0 5 10 15 20 25 30 35 Alta 5 10 15 20 25 30 35 8

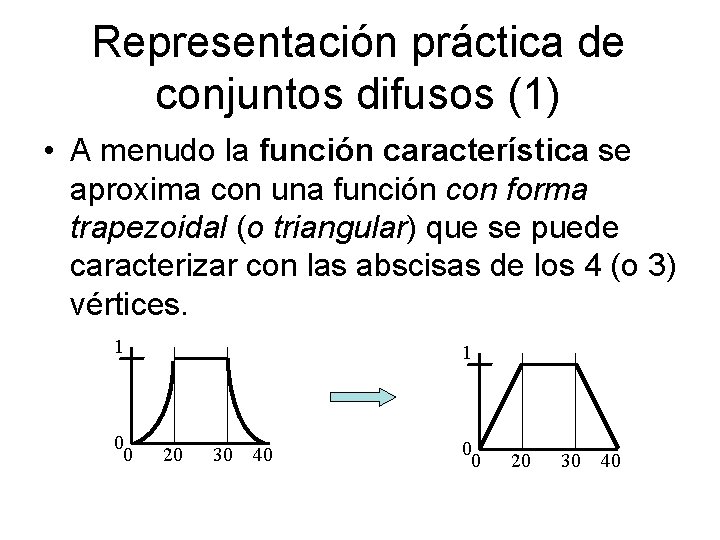
Representación práctica de conjuntos difusos (1) • A menudo la función característica se aproxima con una función con forma trapezoidal (o triangular) que se puede caracterizar con las abscisas de los 4 (o 3) vértices. 1 0 0 1 20 30 40 0 0 20 30 40

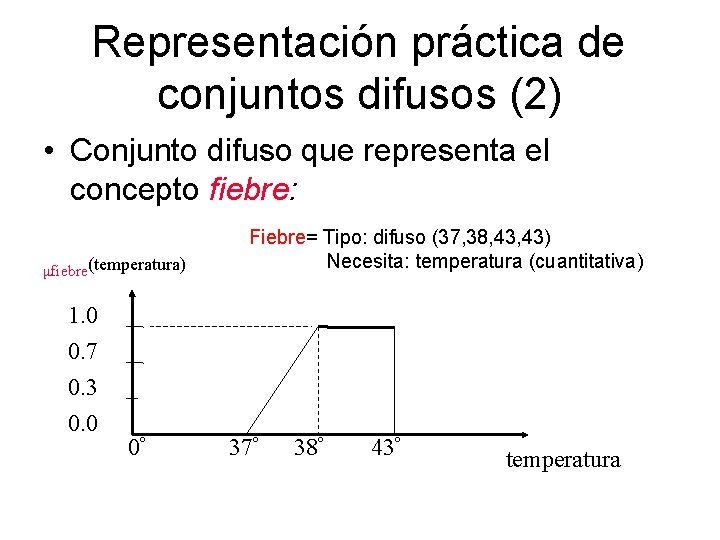
Representación práctica de conjuntos difusos (2) • Conjunto difuso que representa el concepto fiebre: μfiebre(temperatura) 1. 0 0. 7 0. 3 0. 0 0º Fiebre= Tipo: difuso (37, 38, 43) Necesita: temperatura (cuantitativa) 37º 38º 43º temperatura

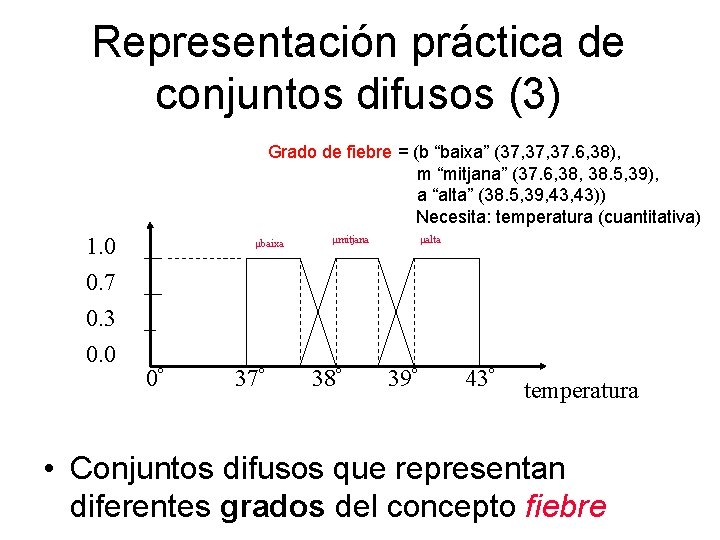
Representación práctica de conjuntos difusos (3) Grado de fiebre = (b “baixa” (37, 37. 6, 38), m “mitjana” (37. 6, 38. 5, 39), a “alta” (38. 5, 39, 43)) Necesita: temperatura (cuantitativa) 1. 0 0. 7 0. 3 0. 0 μbaixa 0º 37º μmitjana 38º μalta 39º 43º temperatura • Conjuntos difusos que representan diferentes grados del concepto fiebre

Representación práctica de conjuntos difusos (4) • [Temperatura es Gelada] • [Temperatura es Molt Freda] • [Temperatura es Fresca] • [Temperatura es Agradable] • [Temperatura es Calorosa] • [Temperatura es Molt Calorosa] • Cada variable tiene un dominio y un conjunto de etiquetas. Cada etiqueta tiene una función característica definida sobre su dominio. • G 1 0 MF F 0 FS A C MC 5 10 15 20 25 30 35

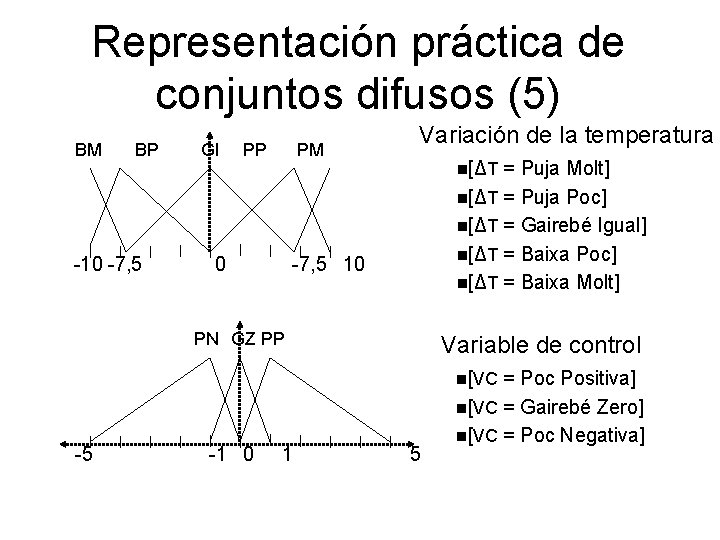
Representación práctica de conjuntos difusos (5) BM BP -10 -7, 5 GI PP PM 0 Variación de la temperatura n[ΔT = Puja Molt] n[ΔT = Puja Poc] n[ΔT = Gairebé Igual] n[ΔT = Baixa Poc] n[ΔT = Baixa Molt] -7, 5 10 PN GZ PP Variable de control n[VC -5 -1 0 1 5 = Poc Positiva] n[VC = Gairebé Zero] n[VC = Poc Negativa]

Lógica difusa Teoría de conjuntos ≡ Lógica de predicados Extensión continua por isomorfismo Teoría de los conjuntos difusos ≡ Lógica difusa Graduación de los valores de veracidad clásicos: falso. . . cierto, en el intervalo continuo [0, 1] 0. . . . . 1

Lógica difusa: conectivas • Las conectivas lógicas difusas (operaciones conjuntos difusos) se definen como funciones continuas en el intervalo [0, 1] que generalizan las conectivas clásicas: – Intersección de conjuntos ≡ P ∧ Q ≡ T-norma (P, Q) – Unión de conjuntos ≡ P ∨ Q ≡ T-conorma (P, Q) – Complemento de un conjunto ≡ ¬P ≡ Función de negación (P) 15

Negación difusa / Complemento “Funciones de negación (fuerte)” N : [0, 1] → [0, 1] • Propiedades: • N(0) = 1 i N(1) = 0 • N(p) ≥ N(q) si p ≤ q • N(N(p)) = p condiciones de contorno monotonía involución • Ejemplos: • N(x) = 1 -x • Nw(x) = (1 -xw)1/w • Nt(x) = (1 -x) / (1+t*x) ∀ w > 0 Familia Yager ∀ t > -1 Familia Sugeno

Conjunción difusa / Intersección “T-Normas” T : [0, 1] x [0, 1] → [0, 1] • Propiedades: • T(p, q) = • T(p, T(q, r)) = • T(p, q) ≤ • T(0, p) = • T(1, p) = • Ejemplos: • T(x, y) = mín • T(x, y) T(q, p) conmutabilidad T(T(p, q), r) asociatividad Τ(r, s) si p ≤ r ∧ q ≤ s monotonía T(p, 0) = 0 elemento absorbente T(p, 1) = p elemento neutro (x, y) = x*y • T(x, y) = màx (0, x+y-1) mínimo producto algebraico diferencia acotada

Disyunción difusa / Unión “T-Conormas” S : [0, 1] x [0, 1] → [0, 1] • Propiedades: • S(p, q) = • S(p, S(q, r)) = • S(p, q) ≤ • S(0, p) = • S(1, p) = • Ejemplos: • S(x, y) = màx S(q, p) conmutabilidad S(S(p, q), r) asociatividad S(r, s) si p ≤ r ∧ q ≤ s monotonía S(p, 0) = p elemento neutro S(p, 1) = 1 elemento absorbente (x, y) • S(x, y) = x+y-x*y • S(x, y) = mín (x+y, 1) máximo suma algebraica suma acotada

Connectives difuses sobre el mateix univers (1) Si F ≡ [X és A] i G ≡ [X és B] amb distribucions de possibilitat ΠA i ΠB definides sobre el mateix univers U F ∧ G ≡ [X és A ∧ B] amb ΠA∧B(u) = T(ΠA(u) , ΠB(u)) Tnorma F ∨ G ≡ [X és A ∨ B] amb ΠA∨ B(u) = S(ΠA(u) , ΠB(u)) Tconorma ¬ F ≡ [X és ¬ A] amb Π¬ A(u) = N(ΠA(u)) Funció de Negació (Funcions d’una mateixa dimensió)

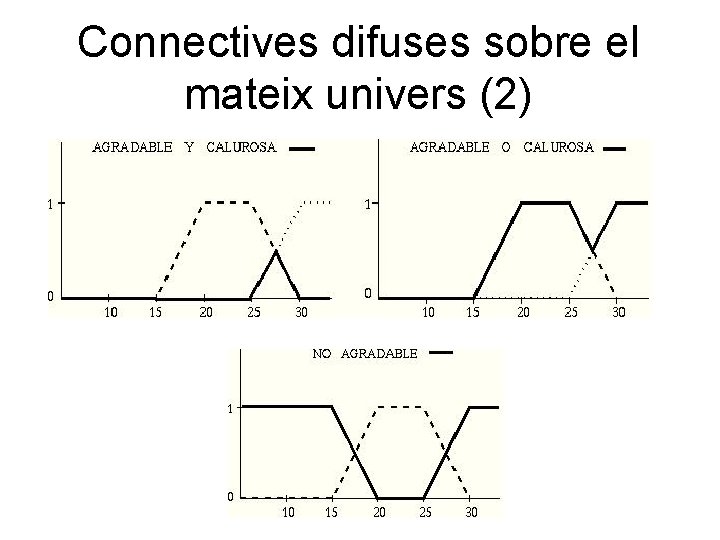
Connectives difuses sobre el mateix univers (2)

Connectives difuses sobre diferents universos (1) Si F ≡ [X és A] i G ≡ [Y és B] amb distribucions de possibilitat ΠA definida sobre U i ΠB definida sobre V, U≠V F ∧ G ≡ [X és A] ∧ [Y és B] amb ΠA∧B(u, v) = T(ΠA(u) , ΠB(v)) Tnorma F ∨ G ≡ [X és A] ∨ [Y és B] amb ΠA∨ B(u, v) = S(ΠA(u) , ΠB(v)) Tconorma (Funcions de dues dimensions diferents)

Connectives difuses sobre diferents universos (2)

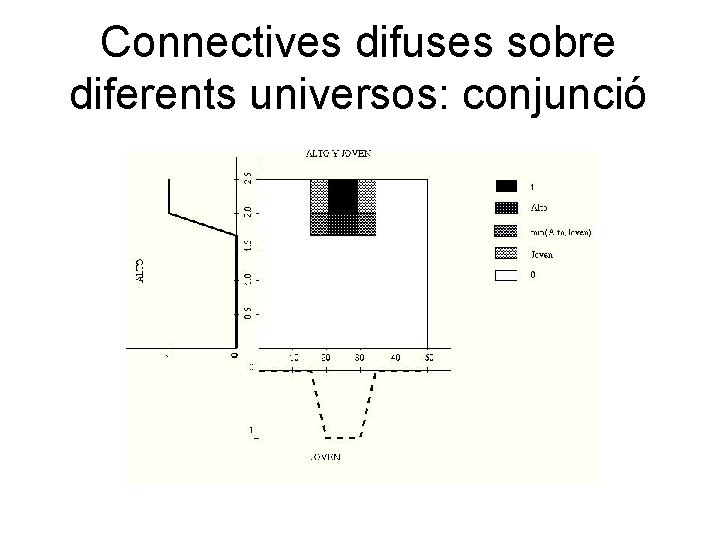
Connectives difuses sobre diferents universos: conjunció

Connectives difuses sobre diferents universos: conjunció

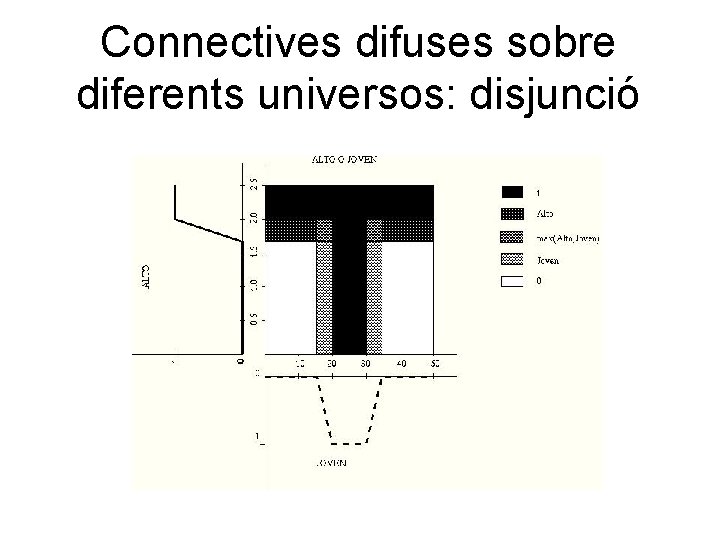
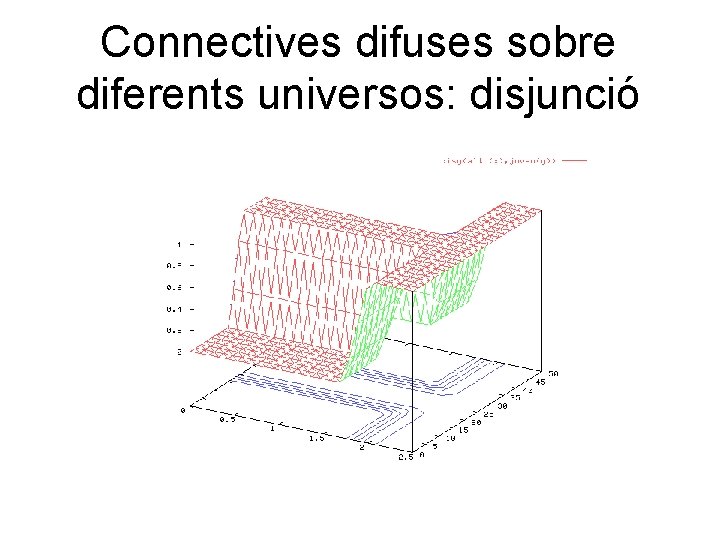
Connectives difuses sobre diferents universos: disjunció

Connectives difuses sobre diferents universos: disjunció

Inferencia difusa con datos precisos • Tenim una base de regles on els àtoms son etiquetes difuses [X = A] R 1: Si R 2: Si R 3: Si R 4: Si T = MC i ΔT = PM llavors VC = PN T = MC i ΔT = PP llavors VC = PN T = A i ΔT = PP llavors VC = GZ • Volem fer inferència amb una combinació de vàries regles: temperatura • [Gelada] • [Molt Freda] • [Fresca] • [Agradable] • [Calenta] • [Molt Calenta] – a partir de valors concrets del domini per algunes variables (les d’alguns antecedents); – combinant la vaguetat/imprecisió d’acord amb les regles i la interpretació de les connectives.

Inferència difusa amb dades precises: Connectives • Interpretació de connectives: – Negació = Complementari (N) – Conjunció = Intersecció difusa = T-normes (T) – Disjunció = Unió difusa = T-conormes (S)

Inferència difusa amb dades precises: Fases 1. Avaluació de l’antecedent de les regles 2. Avaluació de les conclusions de les regles 3. Combinació de les conclusions de les regles 4. Nitidificació (pas de conjunt difús a valor precís)

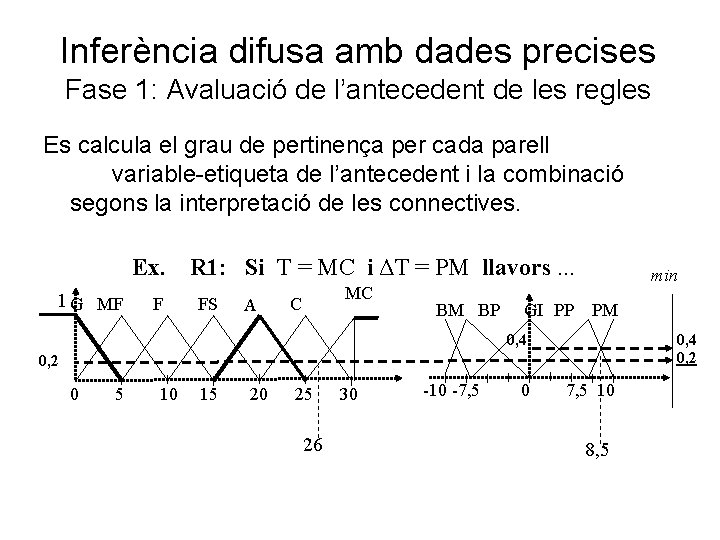
Inferència difusa amb dades precises Fase 1: Avaluació de l’antecedent de les regles Es calcula el grau de pertinença per cada parell variable-etiqueta de l’antecedent i la combinació segons la interpretació de les connectives. Ex. 1 G MF F R 1: Si T = MC i ΔT = PM llavors. . . FS A MC C BM BP min GI PP PM 0, 4 0, 2 0 5 10 15 20 25 26 30 -10 -7, 5 0 7, 5 10 8, 5

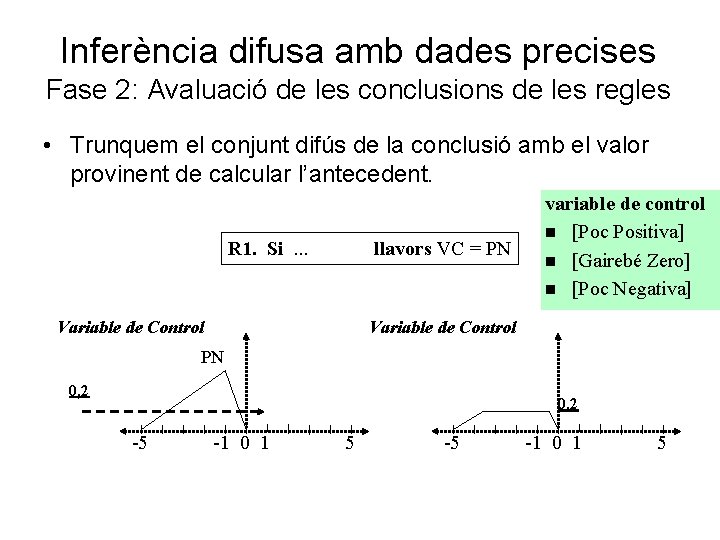
Inferència difusa amb dades precises Fase 2: Avaluació de les conclusions de les regles • Trunquem el conjunt difús de la conclusió amb el valor provinent de calcular l’antecedent. R 1. Si. . . llavors VC = PN Variable de Control variable de control n [Poc Positiva] n [Gairebé Zero] n [Poc Negativa] Variable de Control PN 0, 2 -5 -1 0 1 5

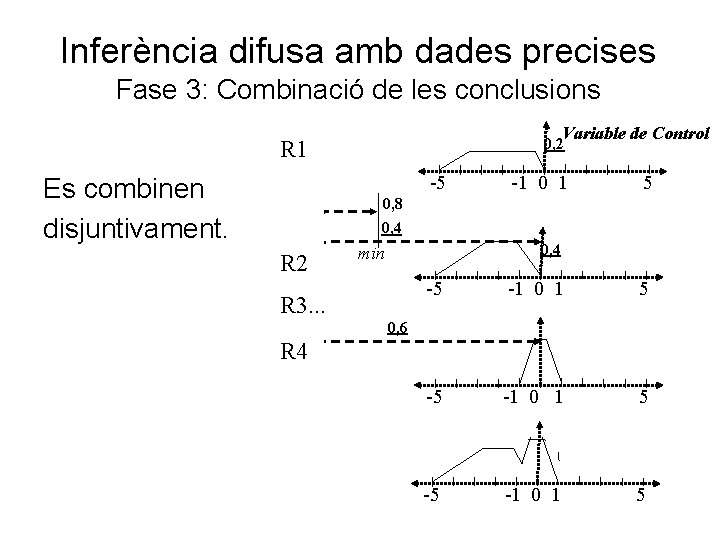
Inferència difusa amb dades precises Fase 3: Combinació de les conclusions Variable de Control 0, 2 R 1 -5 Es combinen disjuntivament. -1 0 1 5 0, 8 0, 4 R 2 0, 4 min R 3. . . -5 -1 0 1 5 0, 6 R 4

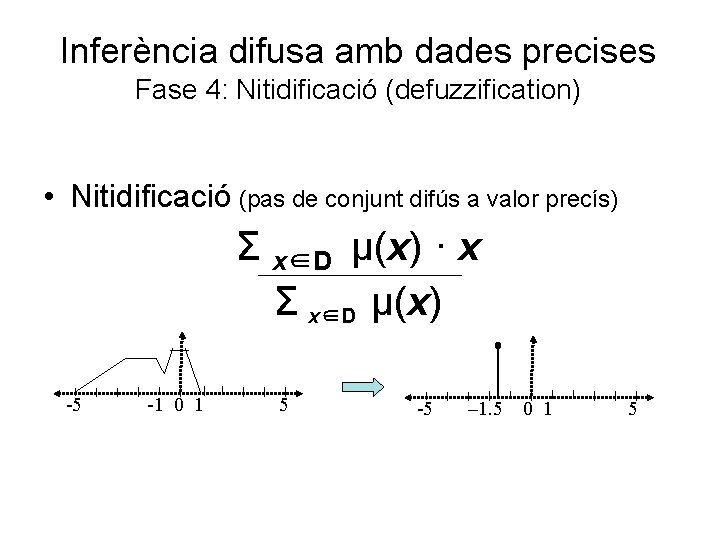
Inferència difusa amb dades precises Fase 4: Nitidificació (defuzzification) • Nitidificació (pas de conjunt difús a valor precís) Σ x∈D μ(x) · x Σ x∈D μ(x) -5 -1 0 1 5 -5 – 1. 5 0 1 5