Institut fr Informatik Seminar Kryptographie So Se 2005

Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen Elliptische Kurven in der Kryptographie 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 1

Gliederung Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern Ø Einleitung Ø Elliptische Kurven über reellen Zahlen Ø Elliptische Kurven über Körper Ø Public-Key Verfahren mittels elliptischer Kurven 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen Ø Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Ø Vergleich ECC und RSA Ø Schlussbetrachtung Ø Literaturverzeichnis 2

Elliptische Kurven in der Kryptographie (ECC) Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Im Jahre 1986 gelang es Neal Koblitz und Victor Miller unabhängig von einander, elliptische Kurven im Bereich Ingo Grebe der Public Key Kryptographie einzusetzen. 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern Mit elliptischen Kurven lassen sich asymmetrische Krypto-Verfahren realisieren. 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis „Im Herzen von ECC steht die Tatsache, dass man auf einer elliptischen Kurve eine abelsche Gruppe definieren kann und dass in dieser Gruppe das diskrete Logarithmus Problem extrem schwer zu lösen ist. “ 3

ECC in Standards Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe 1. Einleitung § IEEE [P 1363] (Institute of Electrical and Electronics Engineers) § Public-Key Verfahren § geeignete Parameter § Schlüsselerzeugung, Schlüsselaustausch 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA § FIPS [186 -2] (Federal Information Processing Standard) § NIST (National Institute of Standards and Technologie) § ECDSA Signaturverfahren 7. Schlussbetrachtung 8. Literaturverzeichnis § Standards der IETF (Internet Engineering Task Force) § SSL/TLS, IPSEC, PKIX, S/MIME, WAP-Protokoll 4

ECC in der Praxis Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe 1. Einleitung Smartcards § enthält privaten Schlüssel § beschränkter Speicherplatz § RSA benötigt >1024 Bit, ECC benötigt 160 Bit § ECC ist schneller beim signieren 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Kryptographie-Plugin „cv act s/mail“ § entwickelt von Cryptovision § eingesetzt vom Bundesamt für Wehrtechnik und Beschaffung § Plugin für e. Mail-Clients ú Verschlüsselung ú digitale Signatur ú kompatibel zu IBM Lotus Notes, Novel Group. Wise, Microsoft Outlook 5

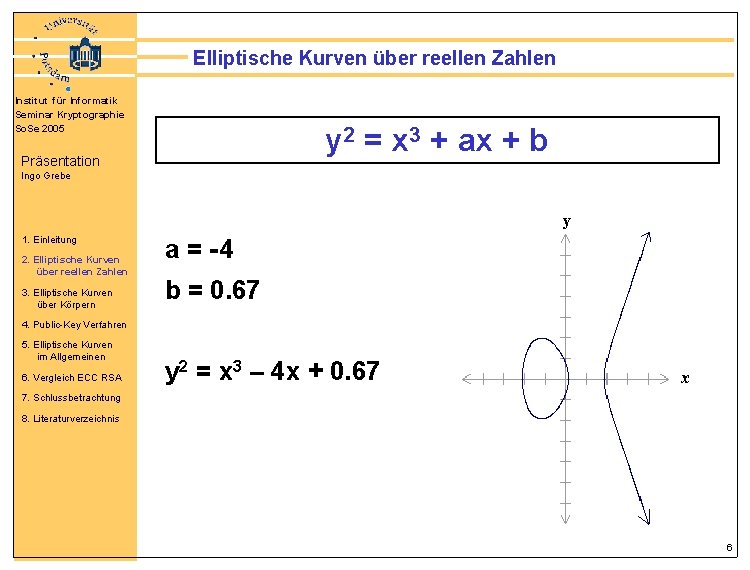
Elliptische Kurven über reellen Zahlen Institut für Informatik Seminar Kryptographie So. Se 2005 y 2 = x 3 + ax + b Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern a = -4 b = 0. 67 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA y 2 = x 3 – 4 x + 0. 67 7. Schlussbetrachtung 8. Literaturverzeichnis 6

Abelsche Gruppe Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe [y 2 = x 3 + ax + b] 2 20 0 ist eine elliptische Unter der Bedingung + 27 b Bedingung: 4 a 34 a +327 b Kurve die Menge aller Lösungen für die Gleichung: y 2 = x 3 + ax + b Punktmit O, dem der Punkt „unendlichen“ zusammen Punkt im O im „unendlichen“. 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern P = (x. P, y. P), Q = (x. Q, y. Q), R = (x. R, y. R) 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis § Operation: + mit P + Q = R § Assoziativität: P + (Q + R) = (P + Q) + R § Kommutativität: P + Q = Q + P § neutrales Element: O mit P + O = O + P = P § Inverses Element: (x, -y) mit P + -P = -P + P = O 7

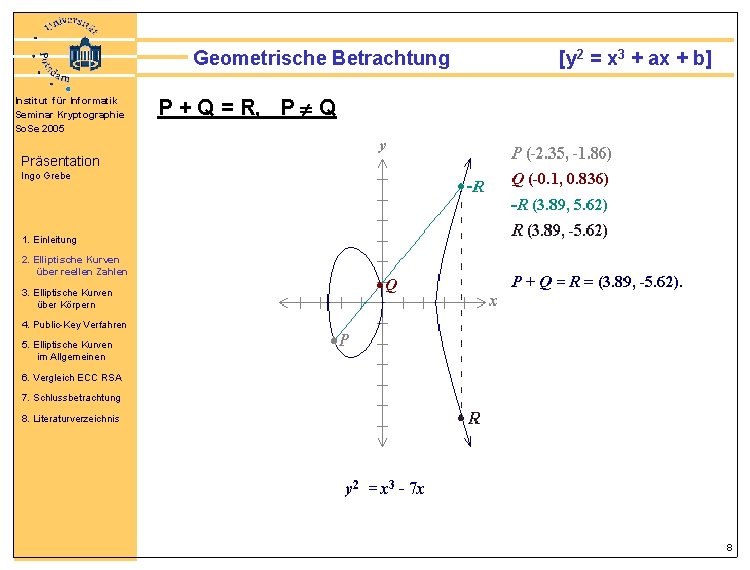
Geometrische Betrachtung Institut für Informatik Seminar Kryptographie So. Se 2005 [y 2 = x 3 + ax + b] P + Q = R, P Q Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 8

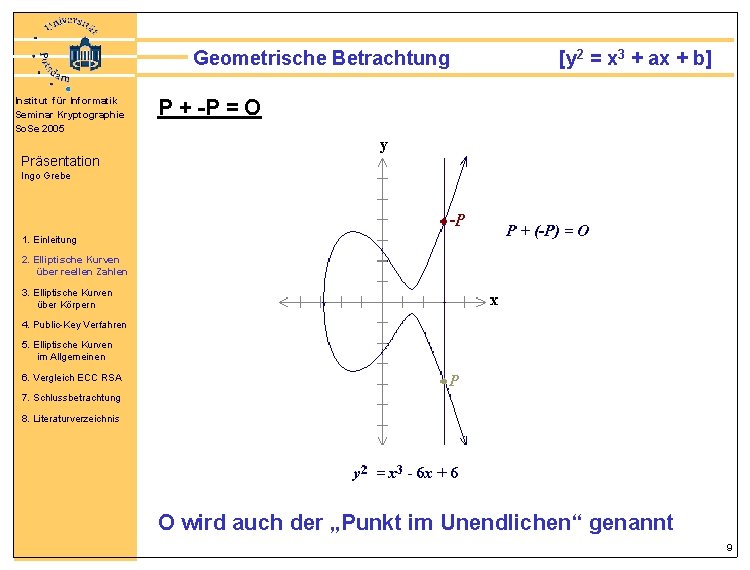
Geometrische Betrachtung Institut für Informatik Seminar Kryptographie So. Se 2005 [y 2 = x 3 + ax + b] P + -P = O Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis O wird auch der „Punkt im Unendlichen“ genannt 9

Geometrische Betrachtung Institut für Informatik Seminar Kryptographie So. Se 2005 [y 2 = x 3 + ax + b] O wir auch der „Punkt im Unendlichen“ genannt Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 10

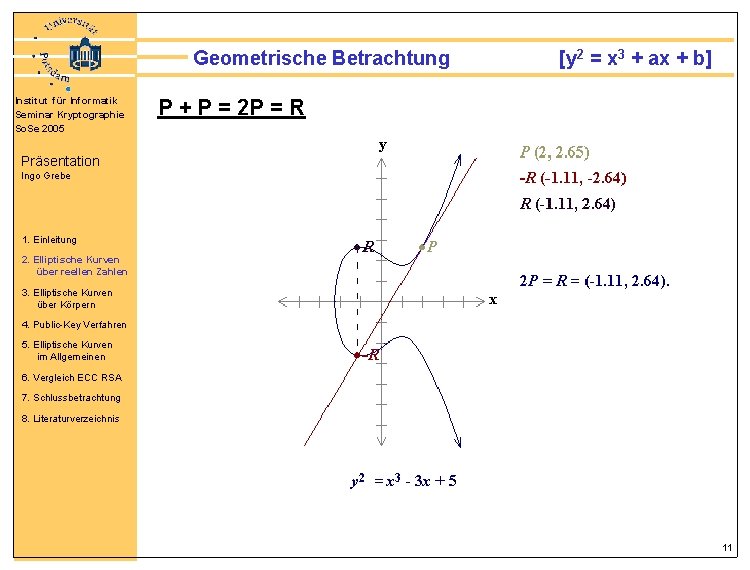
Geometrische Betrachtung Institut für Informatik Seminar Kryptographie So. Se 2005 [y 2 = x 3 + ax + b] P + P = 2 P = R Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 11

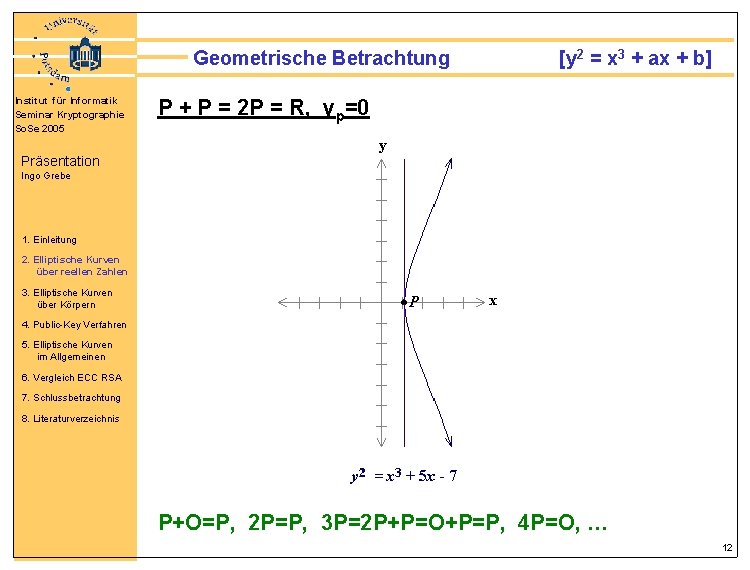
Geometrische Betrachtung Institut für Informatik Seminar Kryptographie So. Se 2005 [y 2 = x 3 + ax + b] P + P = 2 P = R, yp=0 Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis P+O=P, 2 P=P, 3 P=2 P+P=O+P=P, 4 P=O, … 12

Algebraische Betrachtung Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe 1. Einleitung [y 2 = x 3 + ax + b] P + Q = R, P=(x. P, y. P), Q=(x. Q, y. Q), R=(x. R, y. R), P Q s = (y. P – y. Q) / (x. P – x. Q) x. R = s 2 – x. P – x. Q s: Steigung der Geraden durch P und Q y. R = -y. P + s (x. P – x. R) 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis P + P = 2 P = R, P=(x. P, y. P), R=(x. R, y. R), y. P 0 s = (3 x. P 2 + a) / (2 y. P) s: Tangente am Punkt P x. R = s 2 – 2 x. P a: Parameter der Kurve y. R = -y. P + s (x. P – x. R) 13

Beispiele Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 1. Definiert die Gleichung y 2 = x 3 – 7 x – 6 eine Elliptische Kurve? Ja! 4 a 3 + 27 b 2 = 4 (-7)3 + 27 (-6)2 = -400 0 2. Ist P=(4, 7) ein Punkt auf der Elliptischen Kurve y 2 = x 3 – 5 x + 5? Ja! 72 = 43 – 5 4 + 5 49 = 64 – 20 + 5 49 = 49 • Berechne P+Q=R für P=(0, -4) und Q=(1, 0) auf y 2 = x 3 – 17 x + 16! s = (y. P – y. Q) / (x. P – x. Q) = (-4 – 0) / (0 – 1) = 4 x. R = s 2 – x. P – x. Q = 42 – 0 – 1 = 15 y. R = -y. P + s (x. P – x. R) = -(-4) + 4 (0 – 15) = -56 P + Q = R = (15, -56) • Berechne 2 P=R für P=(4, 20) auf y 2 = x 3 – 17 x + 16! s = (3 x. P 2 + a) / (2 y. P) = (3 42 + (-17)) / (2 20) = 4. 475 x. R = s 2 – 2 x. P = 4. 4752 – 2 4 = 12. 022 y. R = -y. P + s (x. P – x. R) = -( 20) + 4. 475 (4 – 12. 022) = -39, 362 2 P = R = (12. 022, -39. 362) 14

Elliptische Kurven über dem Körper FP Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern Wichtig für Kryptographie § endliche Gruppe (Diskreter Logarithmus) § schnelle und präzise Berechnungen Elliptische Kurven über reellen Zahlen haben keine endliche Anzahl an Punkten, sind langsam in ihrer Berechnung und es treten Rundungsfehler auf. 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Primzahlkörper FP § p-1 Elemente, p ist Primzahl § keine Rundungsfehler § y 2 mod p = x 3 + ax + b mod p, a, b FP § 4 a 3 + 27 b 2 mod p 0 15

Beispiel Institut für Informatik Seminar Kryptographie So. Se 2005 [y 2 = x 3 + x] über F 23 Körper F 23, y 2 = x 3 + x, P = (9, 5) y 2 mod p = x 3 + x mod p Präsentation 25 mod 23 = 729 + 9 mod 23 Ingo Grebe 2=2 Punkt P=(9, 5) erfüllt y 2 = x 3 + x 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Es gibt insgesamt 23 Punkte auf der Kurve y 2 = x 3 + x: (0, 0) (1, 5) (13, 18) (1, 18) (9, 5) (9, 18) (11, 10) (11, 13) (15, 20) (16, 8) (16, 15) (17, 10) (17, 13) (18, 10) (18, 13) (19, 1) (19, 22) (20, 4) (20, 19) (21, 6) (21, 17) 16

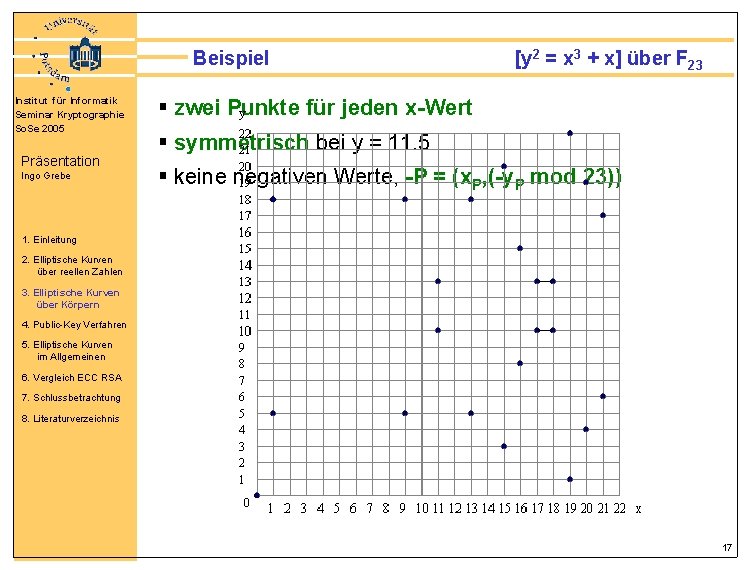
Beispiel Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe [y 2 = x 3 + x] über F 23 § zwei Punkte für jeden x-Wert § symmetrisch bei y = 11. 5 § keine negativen Werte, -P = (x. P, (-y. P mod 23)) 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 17

Algebraische Betrachtung Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe 1. Einleitung [y 2 = x 3 + ax + b] über FP P + Q = R, P=(x. P, y. P), Q=(x. Q, y. Q), R=(x. R, y. R), P Q s = (y. P – y. Q) / (x. P – x. Q) mod p x. R = s 2 – x. P – x. Q mod p s: Steigung der Geraden durch P und Q y. R = -y. P + s (x. P – x. R) mod p 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis P + P = 2 P = R, P=(x. P, y. P), R=(x. R, y. R), y. P 0 s = (3 x. P 2 + a) / (2 y. P) mod p s: Tangente am Punkt P x. R = s 2 – 2 x. P mod p a: Parameter der Kurve y. R = -y. P + s (x. P – x. R) mod p 18

Beispiele Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 1. Definiert die Gleichung y 2=x 3+10 x+5 eine Elliptische Kurve über F 17? Nein! 4 a 3 + 27 b 2 mod p = 4 (10)3 + 27 (5)2 mod 17 = 4675 mod 17 = 0 2. Liegt P=(2, 0) auf der Elliptischen Kurve y 2 = x 3 + x + 7 über F 17? Ja! 02 mod 17 = 23 + 2 + 7 mod 17 0 mod 17 = 17 mod 17 0=0 • Berechne P+Q=R für P=(2, 0) und Q=(1, 3) auf y 2= x 3+ x + 7 über F 17! s = (y. P – y. Q) / (x. P – x. Q) mod p = (0 – 3) / (2 – 1) mod 17 = 14 x. R = s 2 – x. P – x. Q mod p = 142 – 1 mod 17 = 193 mod 17 = 6 y. R = -y. P + s (x. P – x. R) mod p = -0 +14 (2 – 6) mod 17 = 12 P + Q = R = (6, 12) • Berechne 2 P=R für P=(1, 3) auf y 2= x 3+ x + 7 über F 17! s = (3 x. P 2 + a) / (2 y. P) mod p = (3+1) 6 -1 mod 17 = 4 3 mod 17 = 12 x. R = s 2 – 2 x. P mod p = 122 – 2 mod 17 = 6 y. R = -y. P + s (x. P – x. R) mod p = -3 + 12 (1 – 6) mod 17 = 5 2 P = R = (6, 5) 19

Elliptische Kurven über dem Körper F 2 m Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe y 2 + xy = x 3 + ax 2 + b, b 0 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren § Bit Strings § Addition mittels XOR-Funktion 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 20

Verwendete Körper Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Theoretisch § jeder endliche Körper kann verwendet werden Ingo Grebe Praktisch 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern § Primzahlkörper FP mit Primzahl p § F 2 m mit 2 m Elementen 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen Unterschiede zwischen FP und F 2 m 6. Vergleich ECC RSA § bisher noch keine Sicherheitsunterschiede 7. Schlussbetrachtung 8. Literaturverzeichnis § FP hat beim Softwareeinsatz Vorteile § F 2 m hat beim Hardwareeinsatz Vorteile 21

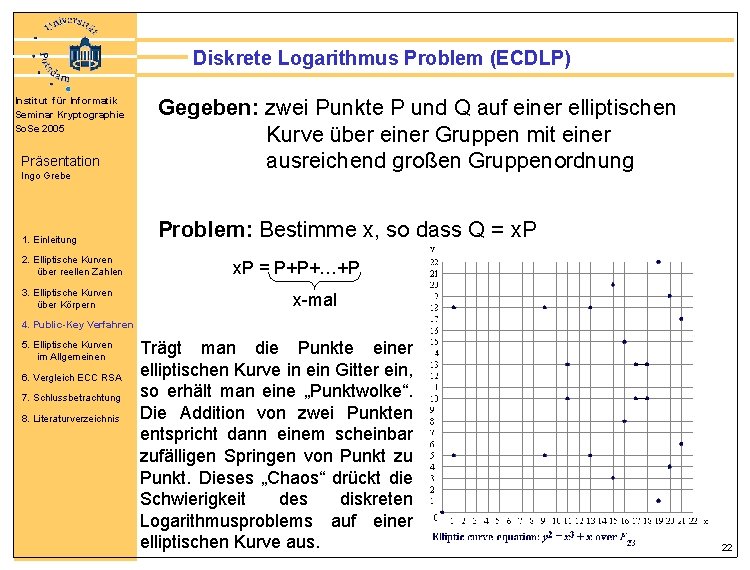
Diskrete Logarithmus Problem (ECDLP) Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern Gegeben: zwei Punkte P und Q auf einer elliptischen Kurve über einer Gruppen mit einer ausreichend großen Gruppenordnung Problem: Bestimme x, so dass Q = x. P = P+P+…+P x-mal 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Trägt man die Punkte einer elliptischen Kurve in ein Gitter ein, so erhält man eine „Punktwolke“. Die Addition von zwei Punkten entspricht dann einem scheinbar zufälligen Springen von Punkt zu Punkt. Dieses „Chaos“ drückt die Schwierigkeit des diskreten Logarithmusproblems auf einer elliptischen Kurve aus. 22

ECDH Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation § einfaches Protokoll für einen Schlüsselaustausch § basiert auf Diffie-Hellman Ingo Grebe Szenario 1. Einleitung § Alice und Bob tauschen geheimen Schlüssel aus 2. Elliptische Kurven über reellen Zahlen § Lauscherin Eve 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Vorraussetzungen § Alice und Bob einigen sich auf gleiche ECC-Parameter ú E: elliptische Kurve ú p: Größe des Körpers FP ú a, b: Koeffizienten der elliptischen Kurve, a, b FP ú G: Punkt auf der elliptischen Kurve E ú n: Ordnung des Punktes G, n muss Primzahl sein 23

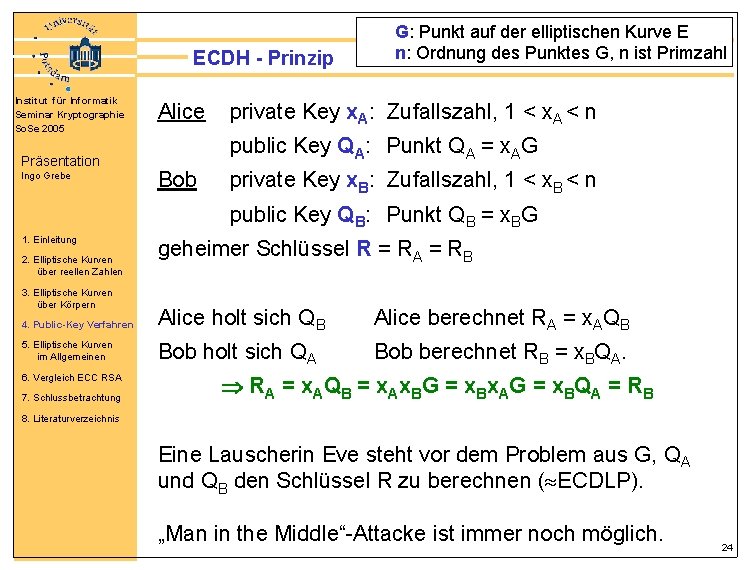
ECDH - Prinzip Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe Alice G: Punkt auf der elliptischen Kurve E n: Ordnung des Punktes G, n ist Primzahl private Key x. A: Zufallszahl, 1 < x. A < n public Key QA: Punkt QA = x. AG Bob private Key x. B: Zufallszahl, 1 < x. B < n public Key QB: Punkt QB = x. BG 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung geheimer Schlüssel R = RA = RB Alice holt sich QB Alice berechnet RA = x. AQB Bob holt sich QA Bob berechnet RB = x. BQA. R A = x AQ B = x Ax BG = x Bx AG = x BQ A = R B 8. Literaturverzeichnis Eine Lauscherin Eve steht vor dem Problem aus G, QA und QB den Schlüssel R zu berechnen ( ECDLP). „Man in the Middle“-Attacke ist immer noch möglich. 24

Elliptische Kurven allgemein Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren Polynom F(x, y) : = x 3 – a 1 xy + a 2 x 2 – a 3 y + a 4 x + a 6 – y 2 Eine elliptische Kurve E über einem Körper K ist eine nicht-singuläre Kurve, definiert als Menge aller Punkte (x, y), mit x, y K, für die gilt F(x, y)=0 zusammen mit dem „Punkt in der Unendlichkeit“ O. 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis elliptische Kurve (Weierstraßgleichung in Normalform) E(K): y 2 + a 1 xy + a 3 y = x 3 + a 2 x 2 + a 4 x + a 6 25

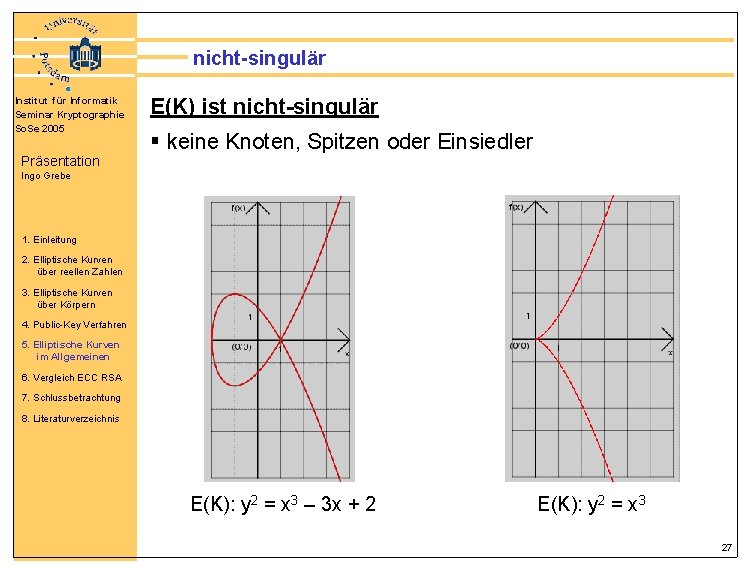
nicht-singulär Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Polynom F(x, y) : = x 3 – a 1 xy + a 2 x 2 – a 3 y + a 4 x + a 6 – y 2 Ingo Grebe elliptische Kurve (Weierstraßgleichung in Normalform) 1. Einleitung 2. Elliptische Kurven über reellen Zahlen E(K): y 2 + a 1 xy + a 3 y = x 3 + a 2 x 2 + a 4 x + a 6 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA E(K) ist nicht-singulär § keine Knoten, Spitzen oder Einsiedler 7. Schlussbetrachtung 8. Literaturverzeichnis F (a, b) 0 x F (a, b) 0 y mit P(a, b) E 26

nicht-singulär Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation E(K) ist nicht-singulär § keine Knoten, Spitzen oder Einsiedler Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis E(K): y 2 = x 3 – 3 x + 2 E(K): y 2 = x 3 27

nicht-singulär Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation char(K) = m falls es eine kleinste natürliche Zahl m gibt, so dass m 1 = 1+1+…+1 = 0 Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis m-mal char(K) 2, 3 E(K): y 2 = x 3 + ax + b E(K) ist nicht-singulär beide Ableitungen 0 F (a, b) = -3 x 2 – a 4 0 x Diskriminante von E 0 F (a, b) = 2 y 0 y 4 a 3 + 27 b 2 0, mit a, b K 28

nicht-singulär Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe E(K) ist nicht-singulär beide Ableitungen 0 F (a, b) = -3 x 2 – a 0 x Diskriminante von E 0 F (a, b) = 2 y 0 y 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 29

nicht-singulär Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe E(K) ist nicht-singulär beide Ableitungen 0 F (a, b) = -3 x 2 – a 0 x Diskriminante von E 0 F (a, b) = 2 y 0 y 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 30

nicht-singulär Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe E(K) ist nicht-singulär beide Ableitungen 0 F (a, b) = -3 x 2 – a 0 x Diskriminante von E 0 F (a, b) = 2 y 0 y 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 31

nicht-singulär Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe E(K) ist nicht-singulär beide Ableitungen 0 F (a, b) = -3 x 2 – a 0 x Diskriminante von E 0 F (a, b) = 2 y 0 y 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 32

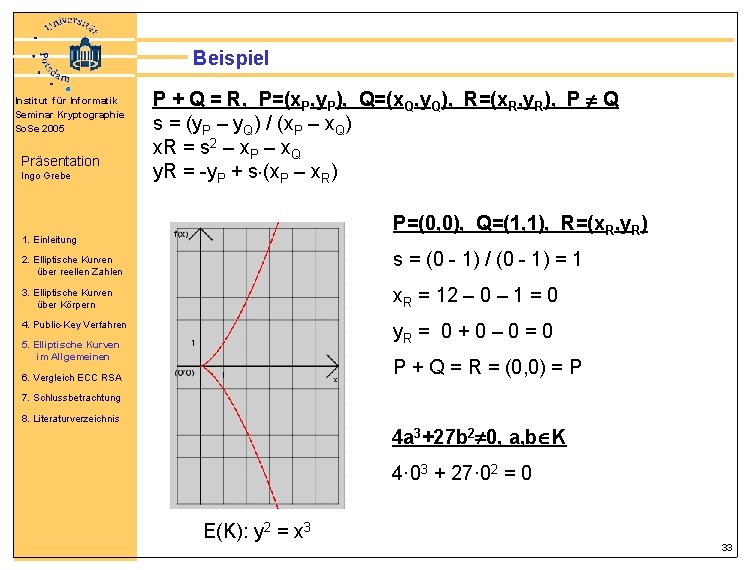
Beispiel Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe P + Q = R, P=(x. P, y. P), Q=(x. Q, y. Q), R=(x. R, y. R), P Q s = (y. P – y. Q) / (x. P – x. Q) x. R = s 2 – x. P – x. Q y. R = -y. P + s (x. P – x. R) P=(0, 0), Q=(1, 1), R=(x. R, y. R) 1. Einleitung s = (0 - 1) / (0 - 1) = 1 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern x. R = 12 – 0 – 1 = 0 4. Public-Key Verfahren y. R = 0 + 0 – 0 = 0 5. Elliptische Kurven im Allgemeinen P + Q = R = (0, 0) = P 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis 4 a 3+27 b 2 0, a, b K 4· 03 + 27· 02 = 0 E(K): y 2 = x 3 33

Ordnung #E(FP) Institut für Informatik Seminar Kryptographie So. Se 2005 Die Anzahl der Punkte einer elliptischen Kurve E(FP) heißt auch Ordnung #E(FP). Präsentation Ingo Grebe Hasse-Schranke 1. Einleitung 2. Elliptische Kurven über reellen Zahlen § es gibt keine allgemeingültige Formel für #E(FP) § Abschätzung mittels Theorem von Hasse 3. Elliptische Kurven über Körpern -2 p + 1 #E(FP) 2 p + 1 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Beispiel -2 23 + 1 #E(F 23) 2 23 + 1 -2 4, 795 + 24 #E(F 23) 2 4, 795 + 23 + 1 14 #E(F 23) 33 34

Untergruppen von E(FP) Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe Untergruppe UP UP : = {k. P | k Z} ist die von P erzeugte zyklische Untergruppe von E(FP). P ist Generator der Gruppe. 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen Ordnung von UP k 0 P = P+P+…+P = O, mit k 0>0 k 0 -mal 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Da P Generator der Gruppe ist, spricht man auch von der Ordnung des Punktes P. 35

Wahl der elliptischen Kurve Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation § Kurven aus Standards § eigene Kurven generieren Ingo Grebe wichtigster Aspekt 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren § große Ordnung n der Punktegruppe § in der Praxis ist n zumeist eine 160 -Bit große Primzahl 160 -Bit = 2160 1, 46 1048 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Testen § Bestimmung der Kurvenordnung (Schoofs Algorithmus) 36

Klassen schwacher Kurven Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe Geringe Ordnung der Kurve Pohlig und Hellman haben gezeigt, wie das ECDLP in diesem Fall in kleinere Probleme unterteilt werden kann. Gegenmittel: Kurve und einen Basispunkt benutzt, so dass die von diesem Punkt erzeugte Untergruppe von großer Primzahlordnung ist. 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen Anomale Kurven § #E(FP) = p Smart, Semaev, Satoh und Araki haben gezeigt, dass für diese Kurven ein Algorithmus mit linearer Laufzeit für das ECDLP existiert. 6. Vergleich ECC RSA 7. Schlussbetrachtung Super-singuläre Kurven 8. Literaturverzeichnis § ord(K) – #E(K) | char(K) Menezes, Okamoto und Vanstone gezeigt, wie man das ECDLP auf das einfache DLP in Erweiterungskörpern von ZP reduzieren kann. Es lässt sich aber sehr leicht feststellen, ob eine bestimmte Kurve supersingulär ist und sich dieser Angriff somit vermeiden. 37

Andere Klassen spezieller Kurven Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Jede Art von Kurve, die auf irgendeine Weise speziell ist, sollte gemieden werden, auch wenn bisher noch kein besonders effizienter Angriff entdeckt worden ist. Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Zu dieser Klasse von Kurven gehören z. B. die Koblitz-Kurven über F 2 m, deren Kurvengleichungen nur die Koeffizienten „ 0“ und „ 1“ enthalten. Diese Kurven sind besonders interessant, da es für sie hoch effiziente Algorithmen für die Punktarithmetik auf ihnen gibt. Jedoch weiß man inzwischen, dass es möglich ist, das Lösen des ECDLP auf ihnen um einen Faktor m zu beschleunigen, was aber immer noch zu vernachlässigen ist. Es gibt Verfahren, die es ermöglichen, Kurven mit einer bestimmten Punktordnung zu erzeugen. Für Kurven, die so erzeugt worden sind, besteht zwar bisher außer den allgemein anwendbaren und extrem langsamen Verfahren noch keine besondere Angriffsmöglichkeit, dennoch bilden sie eine „besondere“ Klasse von Kurven, so dass man solch eine Angriffsmöglichkeit in der Zukunft nicht ausschließen kann. 38

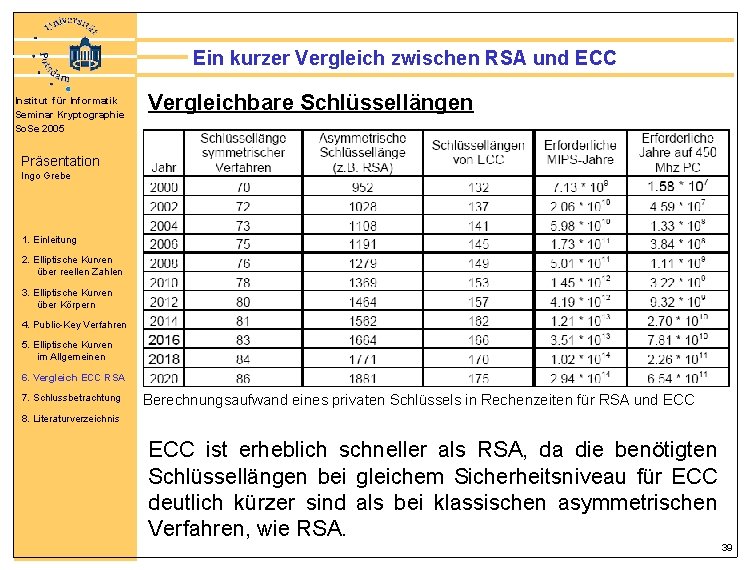
Ein kurzer Vergleich zwischen RSA und ECC Institut für Informatik Seminar Kryptographie So. Se 2005 Vergleichbare Schlüssellängen Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung Berechnungsaufwand eines privaten Schlüssels in Rechenzeiten für RSA und ECC 8. Literaturverzeichnis ECC ist erheblich schneller als RSA, da die benötigten Schlüssellängen bei gleichem Sicherheitsniveau für ECC deutlich kürzer sind als bei klassischen asymmetrischen Verfahren, wie RSA. 39

Ein kurzer Vergleich zwischen RSA und ECC Institut für Informatik Seminar Kryptographie So. Se 2005 Präsentation Ingo Grebe Einsatz des privaten Schlüssels Dennoch liegt es in der Natur der beiden Systeme, dass ECC vor allem für die Aufgaben, die den Einsatz des privaten Schlüssels bedürfen, also digitales Signieren und Entschlüsseln, i. A. um wenigstens einen Faktor 4 schneller ist. 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Bei der Überprüfung einer Signatur oder dem Verschlüsseln ist hingegen RSA um einen ähnlichen Faktor schneller. Dieser Unterschied rührt vor allem daher, dass der öffentliche RSA Exponent meist bewusst so gewählt wird, dass möglichst effektiv gerechnet werden kann, wohingegen der sich daraus ergebende private Exponent keine Geschwindigkeitsvorteile mit sich bringt. 40

Schlussbetrachtung Institut für Informatik Seminar Kryptographie So. Se 2005 Ziel dieser Folien ist es, einen Überblick über die Kryptographie basierend auf elliptischen Kurven zu geben. Präsentation Ingo Grebe 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren 5. Elliptische Kurven im Allgemeinen Zu den hier gegebenen mathematische Ausführungen ist zu sagen, das elliptische Kurven und die zugrunde liegende Mathematik nicht annähernd vollständig erklärt worden sind. So lässt sich beispielsweise der Punkt O in den projektiven Raum einbetten und hat somit auch konkrete Koordinaten und nicht nur die Hilfskonstruktion, die den Punkt im unendlich Fernen der perspektivischen Darstellung erscheinen lässt. 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Elliptische Kurven lassen sich nicht nur zur Kryptographie verwenden, sondern es existieren auch Verfahren basieren auf elliptischen Kurven, die zur Faktorisierung oder zum Primzahlnachweis dienen. 41

Literaturverzeichnis Institut für Informatik Seminar Kryptographie So. Se 2005 Ø „Elliptische Kurven in der Kryptographie“ A. Werner, Springer, 2002 Präsentation Ingo Grebe Ø „Cryptography: Theory and Practice“ 1. Einleitung 2. Elliptische Kurven über reellen Zahlen 3. Elliptische Kurven über Körpern 4. Public-Key Verfahren D. Stinson, Chapman&Hall/CRC, 2002 Ø „ECC Cryptography Tutorial“ Certicom, http: //www. certicom. com 5. Elliptische Kurven im Allgemeinen 6. Vergleich ECC RSA 7. Schlussbetrachtung 8. Literaturverzeichnis Ø „ECC – Elliptic Curve Cryptography“ Cryptovision Gmb. H, http: //www. cryptovision. com Ø „Krypto-Verfahren basierend auf elliptischen Kurven “ T. Laubrock, http: //www. laubrock. de, 1999 42