Induction of decision trees L Orseau Induction of

Induction of decision trees L. Orseau Induction of Decision Trees Laurent Orseau (laurent. orseau@agroparistech. fr) Agro. Paris. Tech based on slides by Antoine Cornuéjols 1

Induction of decision trees • Task Learning a discrimination function for patterns of several classes • Protocol Supervised learning by greedy iterative approximation • Criterion of success Classification error rate • Inputs Attribute-value data (space with N dimensions) • Target functions Decision trees L. Orseau 2

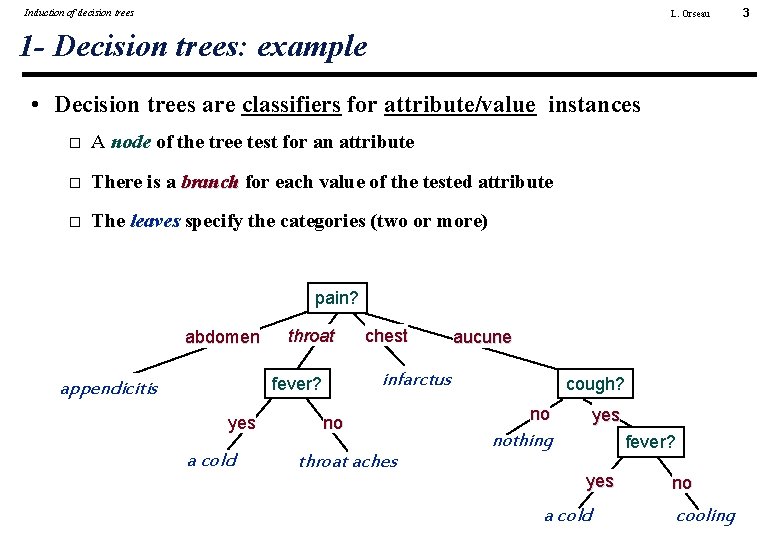
Induction of decision trees L. Orseau 1 - Decision trees: example • Decision trees are classifiers for attribute/value instances A node of the tree test for an attribute There is a branch for each value of the tested attribute The leaves specify the categories (two or more) pain? abdomen throat yes a cold aucune infarctus fever? appendicitis chest no throat aches cough? no yes nothing fever? yes a cold no cooling 3

Induction of decision trees L. Orseau 1 - Decision trees: the problem • Each instance is described by an attribute/value vector Marie Fred Julie Elvis Cough no no yes Fever yes yes no Weight normal thin obese Pain throat abdomen none chest • Input: an set of instances with their class (given by an expert) Marie Fred. . . Cough no no Fever yes Weight normal Pain throat abdomen Diagnostic a cold appendicitis • Learning algorithm must build a decision tree E. g. a decision tree for diagnostic (common application in Machine Learning) 4

Induction of decision trees L. Orseau 1 - Decision trees: expressive power • The choice of the attributes is very important! • If a crucial attribute is not represented Not possible to induce a good decision tree • If two instances have the same representation but belong to two different classes, the language of the instances (attributes) is said to be inadequate. Marie Polo. . . Cough no no Fever yes Weight normal Pain abdomen inadequate language Diagnostic a cold appendicitis 5

Induction of decision trees L. Orseau 6 1 - Decision trees: expressive power • Any boolean function can be represented with a decision tree – Note: with 6 boolean attributes, there about 1. 8*10^19 boolean functions… • Depending on the functions to represent, the trees are more or less large E. g. “parity” and “majority” function: exponential growth Sometimes a single node is enough • Limited to propositional logic (only attribute-value, no relation) • A tree can be represented by a disjunction of rules: DT 4 bird) (Si Feathers = no OR (Si Feathers = yes Alors Classe= not-bird) AND Color= brown Alors Classe= not- OR (Si Feathers = yes AND Color= B&W Alors Classe= bird) AND Color= yellow Alors Classe=

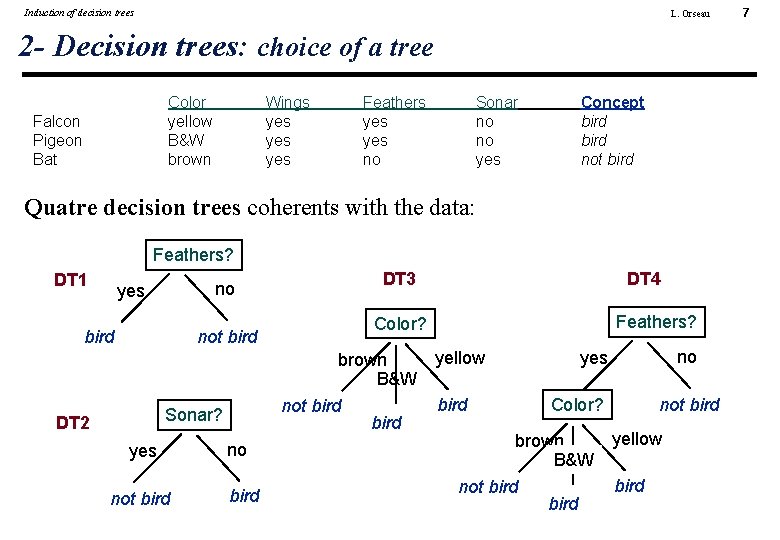
Induction of decision trees L. Orseau 2 - Decision trees: choice of a tree Color yellow B&W brown Falcon Pigeon Bat Wings yes yes Feathers yes no Sonar no no yes Concept bird not bird Quatre decision trees coherents with the data: Feathers? DT 1 no yes bird not bird yes not bird DT 4 Feathers? Color? yellow brown B&W bird not bird Sonar? DT 2 DT 3 no bird no yes Color? not bird yellow brown B&W bird not bird 7

Induction of decision trees L. Orseau 2 - Decision trees: the choice of a tree • When the langage is adequate, it is always possible to build a decision trees that correctly classifies all the training examples. • There are often many correct decision trees. Ø How to give a value to a tree? • Enumeration of all trees is not possible (NP-completeness) for binary trees Ø Requires a constructive iterative method 8

Induction of decision trees L. Orseau 2 - What model for generalization? • Among all possible coherent hypotheses, which one to choose for a good generalization? Is the intuitive answer… . . . confirmed by theory? • Some learnability theory [Vapnik, 82, 89, 95] Consistence of the empirical risk minimization (ERM) Principle of structural risk minimization (SRM) • In short, trees must be short Ø How? Methods of induction of decision trees 9

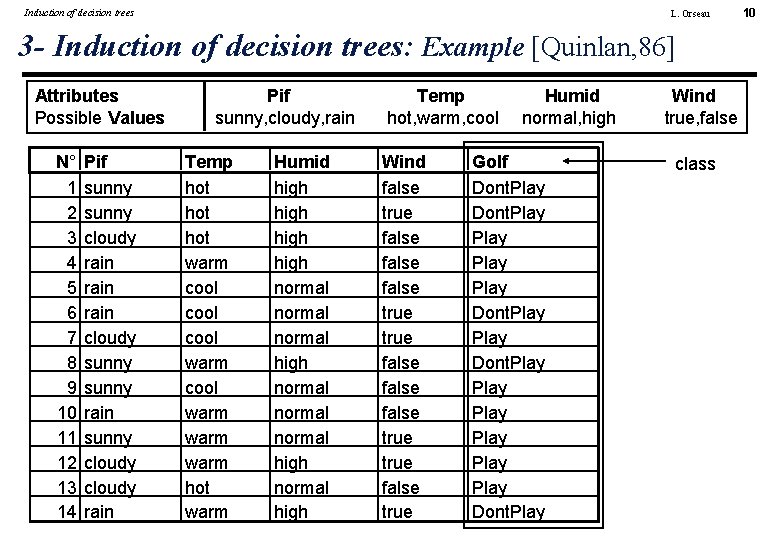
Induction of decision trees L. Orseau 3 - Induction of decision trees: Example [Quinlan, 86] Attributes Possible Values N° 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Pif sunny cloudy rain cloudy sunny rain sunny cloudy rain Pif sunny, cloudy, rain Temp hot hot warm cool warm hot warm Humid high normal normal high Temp hot, warm, cool Wind false true false false true false true Humid normal, high Golf Dont. Play Play Play Play Dont. Play Wind true, false class 10

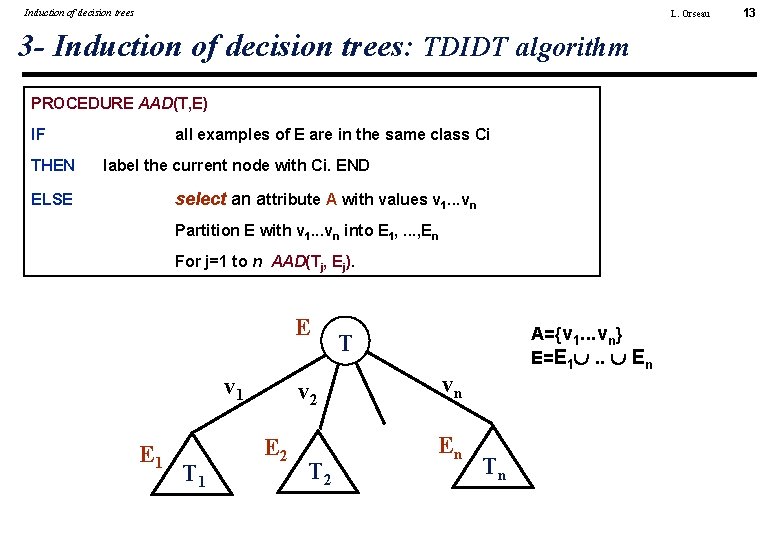
Induction of decision trees L. Orseau 3 - Induction of decision trees • Strategy: Top-down induction: TDIDT Best first search, no backtracking, with a evaluation function Recursive choice of an attribute to test until stopping criterion • Operation: Choose the first attribute as the root of the tree: the most informative one Then, iterate with same operation on all sub-nodes recursive algorithm 11

Induction of decision trees L. Orseau 3 - Induction of decision trees: example • If we choose attribute Temp? . . . + - N° 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Pif sunny cloudy rain cloudy sunny rain sunny cloudy rain Temp hot hot warm cool warm hot warm Humid high normal normal high J 3, J 4, J 5, J 7, J 9, J 10, J 11, J 12, J 13 J 1, J 2, J 6, J 8, J 14 Temp? hot + - J 3, J 13 J 1, J 2 warm + J 4, J 10, J 11, J 13 - J 8, J 14 cool + - J 5, J 7, J 9 J 6 Wind false true false false true false true Golf Dont. Play Play Play Play Dont. Play 12

Induction of decision trees L. Orseau 3 - Induction of decision trees: TDIDT algorithm PROCEDURE AAD(T, E) IF THEN all examples of E are in the same class Ci label the current node with Ci. END select an attribute A with values v 1. . . vn ELSE Partition E with v 1. . . vn into E 1, . . . , En For j=1 to n AAD(Tj, Ej). E v 1 E 1 T 1 v 2 E 2 T 2 A={v 1. . . vn} E=E 1 . . En T vn En Tn 13

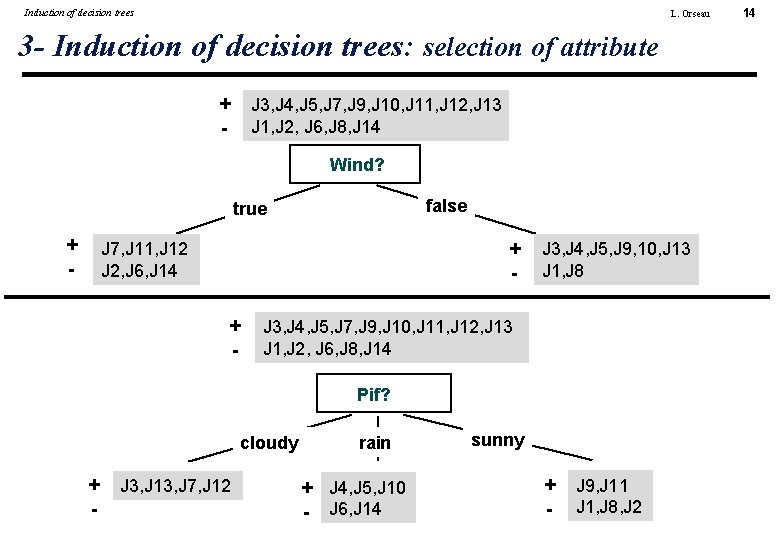
Induction of decision trees L. Orseau 3 - Induction of decision trees: selection of attribute + - J 3, J 4, J 5, J 7, J 9, J 10, J 11, J 12, J 13 J 1, J 2, J 6, J 8, J 14 Wind? false true + - J 7, J 11, J 12 J 2, J 6, J 14 + - J 3, J 4, J 5, J 9, 10, J 13 J 1, J 8 J 3, J 4, J 5, J 7, J 9, J 10, J 11, J 12, J 13 J 1, J 2, J 6, J 8, J 14 Pif? cloudy + J 3, J 13, J 7, J 12 - rain + J 4, J 5, J 10 - J 6, J 14 sunny + J 9, J 11 - J 1, J 8, J 2 14

Induction of decision trees L. Orseau 3 - La selection of a warm attribute of test • How to build a “simple” tree? Simple tree: Minimize expected number of tests to class a new object How to translate this global criterion into a local choice procedure? • Criterions to choose a node Ø We don't know how to associate a local criterion to the global objective criterion Use of heuristics Notion of measure of ”impurity” – Gini Index – Entropic criterion (ID 3, C 4. 5, C 5. 0) –. . . 15

Induction of decision trees 3 - Measure of impurity: the Gini index • Ideally: Null measure if all populations are homogeneous Maximal measure if the populations are maximally mixed • Gini Index [Breiman and al. , 84] L. Orseau 16

Induction of decision trees 3 - The entropic criterion L. Orseau (1/3) • Boltzmann's entropy. . . • . . . and Shannon's entropy Shannon, 1949, proposed a measure of entropy for discrete probability distributions. Expresses the quantity of information, i. e. the number of bits need to specify the distribution Information entropy: where pi is the probability of class Ci. 17

Induction of decision trees L. Orseau 3 - The entropic criterion (2/3) Information entropy of S (in C classes): p(ci): probability of the class ci • • • Null when only one class The most equiprobable the classes are, the highest I(S) = log 2(k) when the k classes are equiprobable • Unit: the bit of information 18

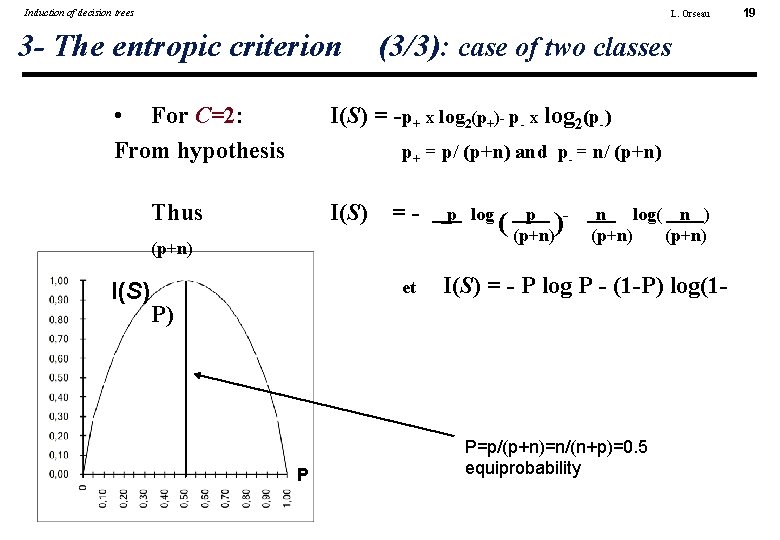
Induction of decision trees L. Orseau 3 - The entropic criterion • For C=2: From hypothesis (3/3): case of two classes I(S) = -p+ x log 2(p+)- p- x log 2(p-) p+ = p/ (p+n) and p- = n/ (p+n) Thus I(S) = - (p+n) I(S) et p log p ( (p+n) )- n log( n ) (p+n) I(S) = - P log P - (1 -P) log(1 - P) P P=p/(p+n)=n/(n+p)=0. 5 equiprobability 19

Induction of decision trees L. Orseau 3 - Entropic gain associated with an attribute |Sv|: size of the sub-population in the branch v of A How is the knowledge of the value of attribute A informative about the class of an example 20

Induction of decision trees L. Orseau 3 - Example (1/4) • Entropy of initial set of examples I(p, n) = - 9/14 log 2(9/14) - 5/14 log 2(5/14) • Entropy of subtrees associated with test on p 1 = 4 n 1 = 0: I(p 1, n 1) = 0 p 2 = 2 n 2 = 3: I(p 2, n 2) = 0. 971 p 3 = 3 n 3 = 2: I(p 3, n 3) = 0. 971 • Entropy of subtrees associated with test on p 1 = 2 n 1 = 2: I(p 1, n 1) = 1 p 2 = 4 n 2 = 2: I(p 2, n 2) = 0. 918 p 3 = 3 n 3 = 1: I(p 3, n 3) = 0. 811 Pif? Temp? 21

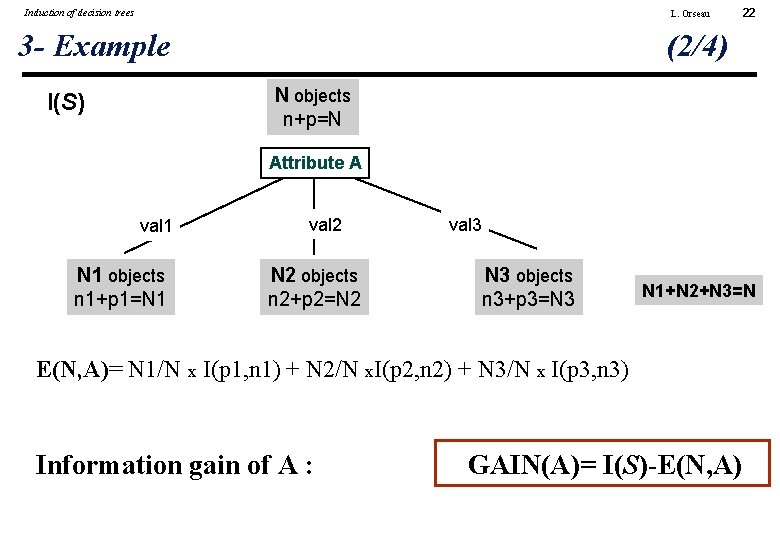
Induction of decision trees L. Orseau 3 - Example 22 (2/4) N objects n+p=N I(S) Attribute A val 1 N 1 objects n 1+p 1=N 1 val 2 N 2 objects n 2+p 2=N 2 val 3 N 3 objects n 3+p 3=N 3 N 1+N 2+N 3=N E(N, A)= N 1/N x I(p 1, n 1) + N 2/N x. I(p 2, n 2) + N 3/N x I(p 3, n 3) Information gain of A : GAIN(A)= I(S)-E(N, A)

Induction of decision trees L. Orseau 3 - Example (3/4) • For the initial examples I(S) = - 9/14 log 2(9/14) - 5/14 log 2(5/14) • Entropy of the tree associated with test on Ø E(Pif) = Pif? 4/14 I(p 1, n 1) + 5/14 I(p 2, n 2) + 5/14 I(p 3, n 3) Ø Gain(Pif) = 0. 940 - 0. 694 = 0. 246 bits Gain(Temp) = 0. 029 bits Gain(Humid) = 0. 151 bits Gain(Wind) = 0. 048 bits Choice of attribute Pif for the first test 23

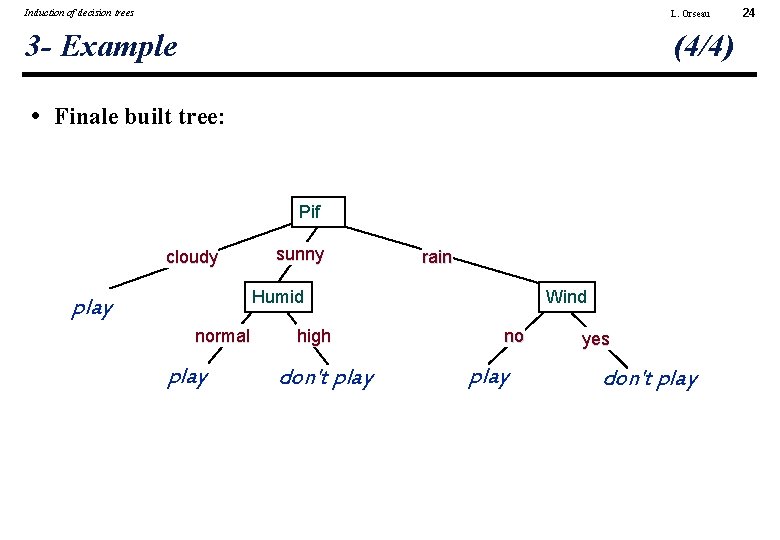
Induction of decision trees L. Orseau 3 - Example (4/4) • Finale built tree: Pif cloudy sunny rain Humid play normal play high don't play Wind no play yes don't play 24

Induction of decision trees L. Orseau 3 - Some TDIDT systems Input: vector of attributes-values associated with each example Output: decision tree • CLS (Hunt, 1966) [analyse of data] • ID 3 (Quinlan 1979) • ACLS (Paterson & Niblett 1983) • ASSISTANT (Bratko 1984) • C 4. 5 (Quinlan 1986) • CART (Breiman, Friedman, Ohlson, Stone, 1984) 25

Induction of decision trees 4 - Potential problems 1. Continuous value attributes 2. Attributes with different branching factors 3. Missing values 4. Overfitting 5. Greedy search 6. Choice of attributes 7. Variance of results: • Different trees from similar data L. Orseau 26

Induction of decision trees L. Orseau 4. 1. Discretization of continuous attribute values 6°C 8°C 14°C 18°C 20°C 28°C 32°C Non Non Oui Oui Non Here, two possible thresholds: 16°C and 30°C attribute Temp>16°C is the most informative, and is kept Temp. Play au golf 27

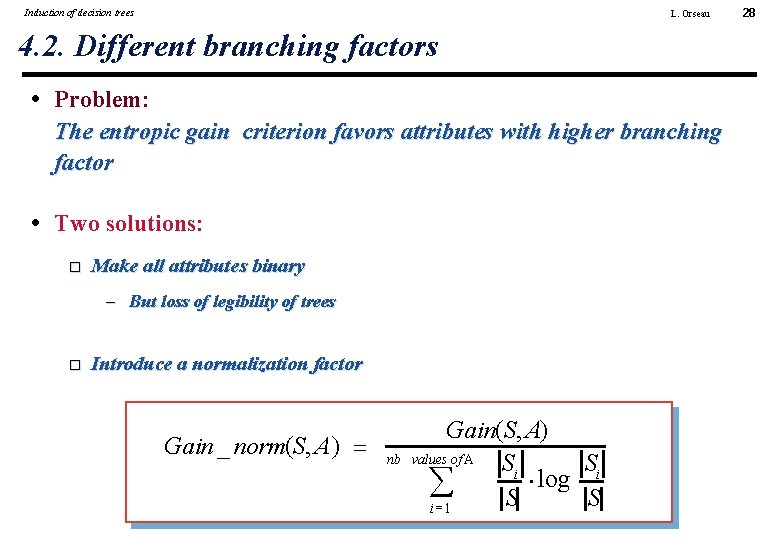
Induction of decision trees L. Orseau 4. 2. Different branching factors • Problem: The entropic gain criterion favors attributes with higher branching factor • Two solutions: Make all attributes binary – But loss of legibility of trees Introduce a normalization factor Gain _ norm(S, A) = nb Gain(S, A) values of A Si Si × log å= S S i 1 28

Induction of decision trees L. Orseau 4. 3. Processing missing values • Let an example x , c(x) for which we don't know the value for attribute A • How to compute gain(S, A)? 1. Take the most frequent value in entire S 2. Take the most frequent value at this node 3. Split example in fictitious examples with the different possible values of A weighted by their respective frequency E. g. if 6 examples at this node take the value A=a 1 and 4 the value A=a 2 A(x) = a 1 with prob=0. 6 and A(x) = a 2 with prob=0. 4 For prediction, class the example with the label of the most probable leaf. 29

Induction of decision trees L. Orseau 5 - The generalization problem Did we learn a good decision tree? • Training set. Ensemble test. • Learning curve • Methods to evaluate generalization On a test set Cross validation – “Leave-one-out” 30

Induction of decision trees 5. 1. Overfitting: Effect of noise on induction • Types of noise Description errors Classification errors “clashes” Missing values • Effects Over-developed tree: too deep, too many leaves L. Orseau 31

Induction of decision trees L. Orseau 5. 1. Overfitting: The generalization problem • Low empirical risk. High real risk. • SRM (Structural Risk Minimization) Justification [Vapnik, 71, 79, 82, 95] – Notion of “capacity” of the hypothesis space – Vapnik-Chervonenkis dimension We must control the hypothesis space 32

Induction of decision trees 5. 1. Control of space H: motivations & strategies • Motivations: Improve generalization performance (SRM) Build a legible model of the data (for experts) • Strategies: 1. Direct control of the size of the induced tree: pruning 2. Modify the state space (trees) in which to search 3. Modify the search algorithm 4. Restrain the data base 5. Translate built trees into another representation L. Orseau 33

Induction of decision trees 5. 2. Overfitting: Controlling the size with pre-pruning • Idea: modify the termination criterion Depth threshold (e. g. [Holte, 93]: threshold =1 or 2) Chi 2 test Laplacian error Low information gain Low number of examples Population of examples not statistically significant Comparison between ”static error” and ” dynamic error” • Problem: often too short-sighted L. Orseau 34

Induction of decision trees L. Orseau 5. 2. Example: Chi 2 test Let a binary attribute A (n) = (n 1, n 2) Null hypothesis (n) = (n 1, n 2) A A P g d (ng 1, ng 2) n 1 = ng 1 + nd 1 n 2 = ng 2 + nd 2 (1 -P) (nd 1, nd 2) P g d (neg 1, neg 2) (1 -P) (ned 1, ned 2) neg 1 = Pn 1 ; ned 1 = (1 -P)n 1 neg 2 = Pn 2 ; ned 2 = (1 -P)n 2 35

Induction of decision trees L. Orseau 5. 3. Overfitting: Controlling the size with post-pruning • Idea: Prune after the construction of whole tree, by replacing subtrees that optimize a pruning criterion on a node. • Many methods. Still lots of research. Minimal Cost-Complexity Pruning (MCCP) (Breiman and al. , 84) Reduced Error Pruning (REP) (Quinlan, 87, 93) Minimum Error Pruning (MEP) (Niblett & Bratko, 86) Critical Value Pruning (CVP) (Mingers, 87) Pessimistic Error Pruning (PEP) (Quinlan, 87) Error-Based Pruning (EBP) (Quinlan, 93) (used in C 4. 5) . . . 36

Induction of decision trees 5. 3 - Cost-Complexity pruning • [Breiman and al. , 84] • Cost-complexity for a tree: L. Orseau 37

Induction of decision trees 6. Forward search • Instead of a greedy search, search n nodes ahead If I choose this node and then … • But exponential growth of the number of computations L. Orseau 38

Induction of decision trees 6. Modification of the search strategy • Idea: no more depth first search • Methods that use a different measure: Minimum Description Length principle – Measure of the complexity of the tree – Measure of the complexity of the examples not coded by the tree – Keep tree that minimizes the sum of these measures Measure of low learnability theory Kolmogorov-Smirnoff measure Class separation measure Mix of selection tests L. Orseau 39

Induction of decision trees L. Orseau 7. Modification of the search space • Modification of the node tests To solve the problems of an inadequate representations Methods of constructive induction (e. g. multivariate tests) E. g. Oblique decision trees • Methods: Numerical Operators – Perceptron trees – Trees and Genetic Programming Logical operators 40

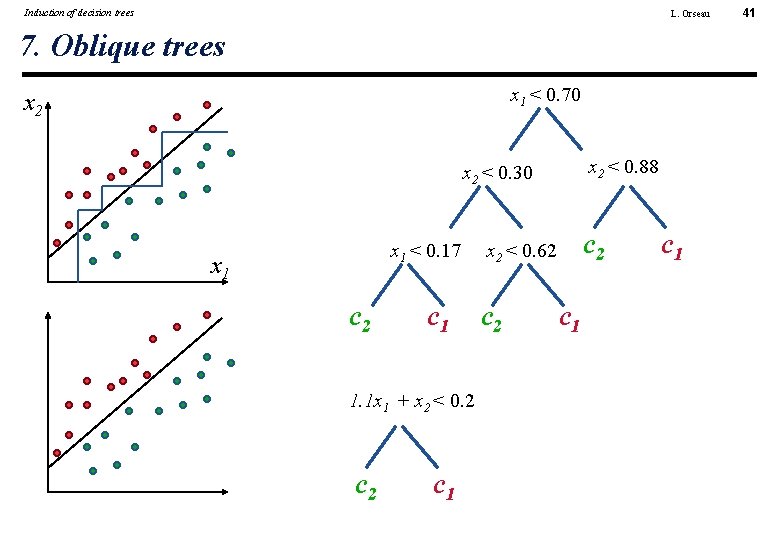
Induction of decision trees L. Orseau 7. Oblique trees x 1 < 0. 70 x 2 < 0. 88 x 2 < 0. 30 x 1 < 0. 17 x 1 c 2 c 1 1. 1 x 1 + x 2 < 0. 2 c 1 c 2 x 2 < 0. 62 c 1 c 1 41

Induction of decision trees L. Orseau 7. Induction of oblique trees • Other cause of leafy trees: an inadequate representation • Solutions: Ask an expert (e. g. chess endgame [Quinlan, 83]) Do an PCA beforehand Other attribute selection method Apply a constructive induction Induction of oblique trees 42

Induction of decision trees L. Orseau 8. Translation into other representations • Idea: Translate a complex tree into a representation where the result is simpler • Translation into decision graphs • Translation rule sets 43

Induction of decision trees 9. Conclusions • Appropriate for: Classification of attribute-value examples Attributes with discrete values Resistance to noise • Strategy: Search by incremental construction of hypothesis Local criterion (gradient) based on statistical criterion • Generates Interpretable decision trees (e. g. production rules) • Requires a control of the size of the tree L. Orseau 44