Trees Chapter 11 Trees Overview Trees are a

Trees

• Chapter 11 – Trees • Overview – Trees are a flexible data structure useful for solving a wide range of problems. 11/4/2020 2

Chapter Objectives • 1. Trees represent data in a hierarchical manner. • 2. Binary search trees allow rapid retrieval by key, plus in-order processing. • 3. Inheritance can be used to model “is-a” relationships and support code reuse.

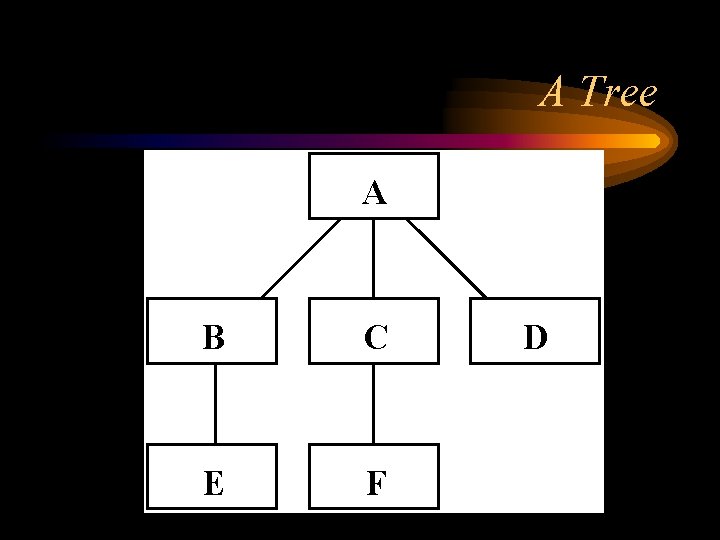
A Tree A B C E F D

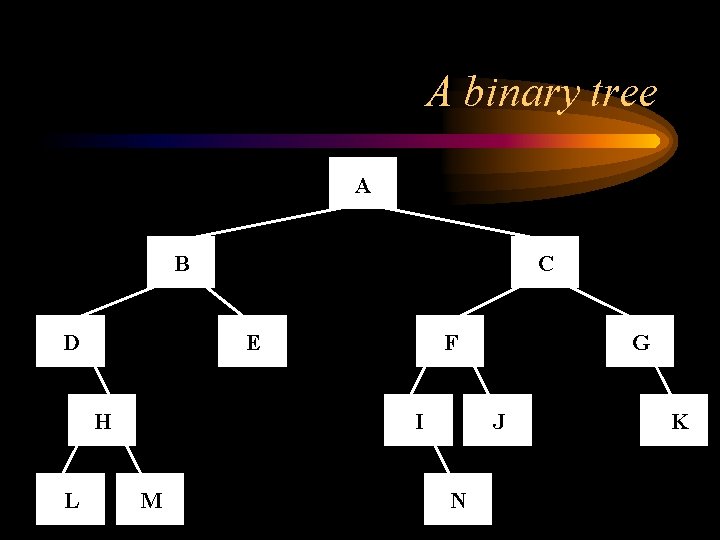
A binary tree A B D E H L C F I M G J N K

Terminology • • • Node - tree element Root - the node at the top Parent/child nodes Siblings - have the same parent Levels - start with 0 Depth - the level of a node Internal nodes - nodes with children Leaves - nodes without children Height - Depth of the deepest leaf Degree - number of child nodes

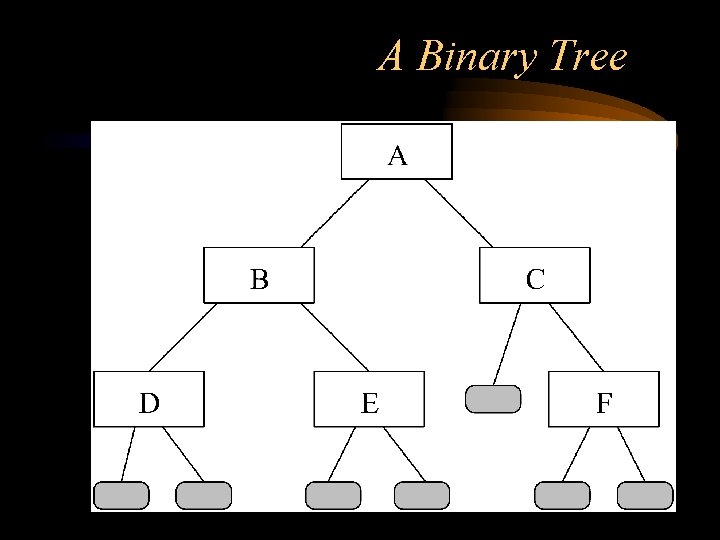
Binary tree definition • • • A binary tree is either: 1. an empty tree; or 2. consists of a node, called a root, and two children, left and right, each of which are themselves binary trees.

A Binary Tree

Two distinct Binary Trees

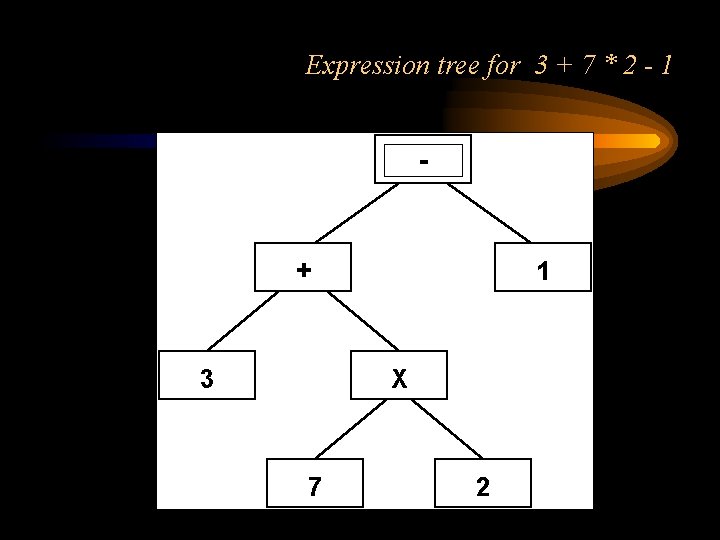
Expression trees • 3+7*2 -1 • 3+(7*2)-1 • (3+(7*2))-1 grouping for * precedence left->right associative + vs. -

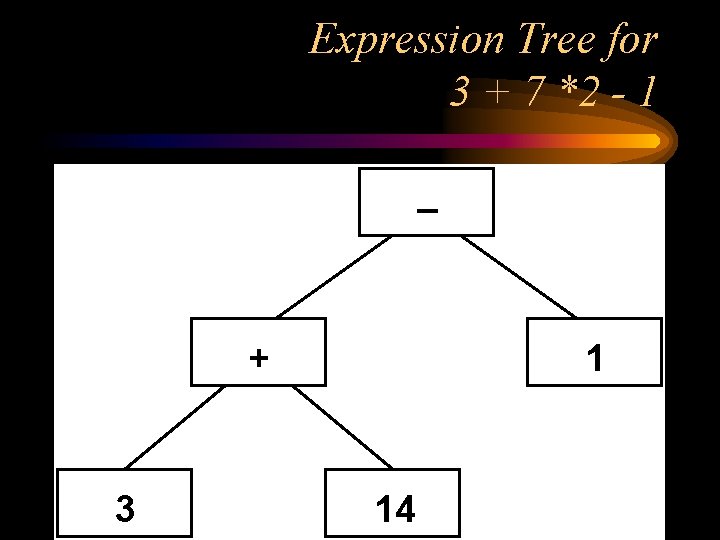
Expression tree for 3 + 7 * 2 - 1 - + 3 1 X 7 2

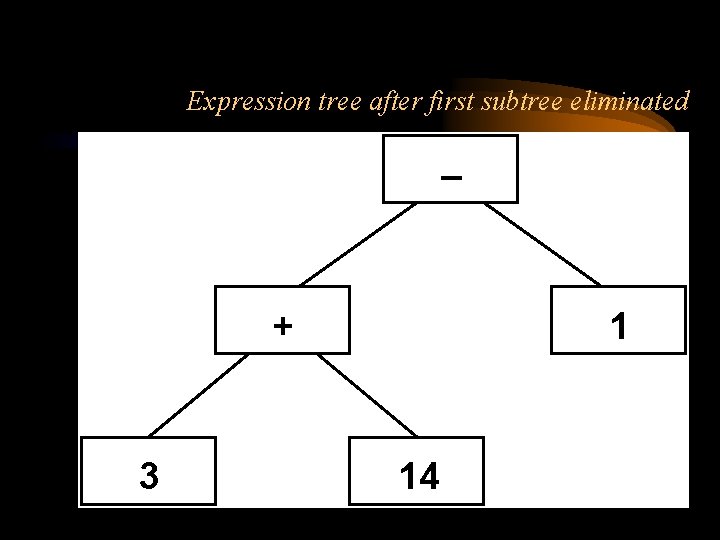
Expression tree after first subtree eliminated + 3 1 14

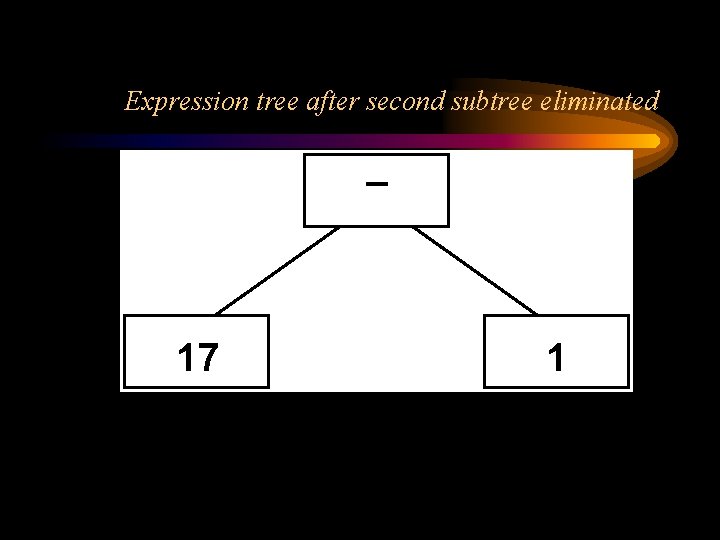
Expression tree after second subtree eliminated 17 1

Final value of expression tree 16

Binary Tree ADT • • • Characteristics • A Binary Tree ADT T stores data of some type (bt. Element. Type Operations is. Empty get. Data insert left right make. Left make. Right

Binary tree interface file • template < class bt. Element. Type > • class Binary. Tree { • public: • Binary. Tree(); • bool is. Empty() const; • // Precondition: None. • // Postcondition: None. • // Returns: true if and only if T is an empty tree

get. Data(), insert() bt. Element. Type get. Data() const; get. Data is an accessor • // Precondition: !this->is. Empty() • // Postcondition: None • // Returns: data associated with the root of the tree • • void insert(const bt. Element. Type & d); • // Precondition: none • // Postconditions: this->get. Data() == d; !this->is. Empty() //

left() and right() • Binary. Tree * left(); • // Precondition: !this->is. Empty() • // Postcondition: None • // Returns: (a pointer to) the left child of T • Binary. Tree * right(); • // Precondition: !this->is. Empty() • // Postcondition: None • // Returns: (a pointer to) the right child of T

make. Left(), make. Right() • void make. Left(Binary. Tree * T 1); • // Precondition: !this->is. Empty(); this->left()->is. Empty() • // Postcondition: this->left() == T 1 • void make. Right(Binary. Tree * T 1); • // Precondition: !this->is. Empty(); this->right()->is. Empty() • // Postcondition: this->right() == T 1

Private section • private: • bool null. Tree; • bt. Element. Type tree. Data; • Binary. Tree * left. Tree; • Binary. Tree * right. Tree; • }; null. Tree { f/t} data left right

Implementation file: constructor • • template < class bt. Element. Type > Binary. Tree < bt. Element. Type > : : Binary. Tree() { null. Tree = true; left. Tree = 0; right. Tree = 0; }

is. Empty() • • • template < class bt. Element. Type > bool Binary. Tree < bt. Element. Type > : : is. Empty() const { return null. Tree; }

get. Data() • • template < class bt. Element. Type > bt. Element. Type Binary. Tree < bt. Element. Type > : : get. Data() const { assert(!is. Empty()); return tree. Data; }

insert() • • • template < class bt. Element. Type > void Binary. Tree < bt. Element. Type > : : insert(const bt. Element. Type & d) { tree. Data = d; if (null. Tree) { null. Tree = false; left. Tree = new Binary. Tree; right. Tree = new Binary. Tree; } }

left() • • • template < class bt. Element. Type > Binary. Tree < bt. Element. Type > * Binary. Tree < bt. Element. Type > : : left() { assert(!is. Empty()); return left. Tree; }

right() • • • template < class bt. Element. Type > Binary. Tree < bt. Element. Type > * Binary. Tree < bt. Element. Type > : : right() { assert(!is. Empty()); return right. Tree; }

make. Left() • • template < class bt. Element. Type > void Binary. Tree < bt. Element. Type > : : make. Left(Binary. Tree * T 1) { assert(!is. Empty()); assert(left()->is. Empty()); delete left(); // could be null. Tree true, w/data left. Tree = T 1; }

make. Right() • • template < class bt. Element. Type > void Binary. Tree < bt. Element. Type > : : make. Right(Binary. Tree * T 1) { assert(!is. Empty()); assert(right()->is. Empty()); delete right(); right. Tree = T 1; }

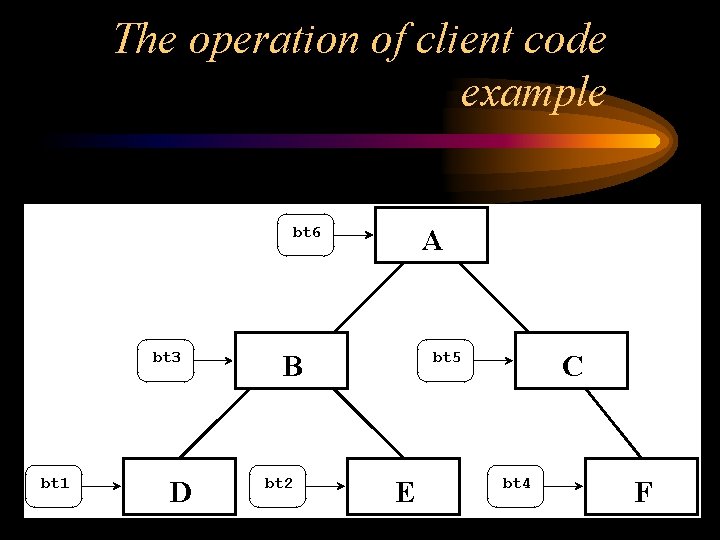
The operation of client code example bt 6 bt 3 bt 1 D A bt 5 B bt 2 E C bt 4 F

Simple client for Binary Tree • • • int main() { typedef Binary. Tree < char > char. Tree; typedef char. Tree * char. Tree. Ptr; // Create left subtree (rooted at B) // Create B's left subtree char. Tree. Ptr bt 1(new char. Tree); bt 1 ->insert('D'); // Create B's right subtree char. Tree. Ptr bt 2(new char. Tree); bt 2 ->insert('E'); D bt 1 E bt 2

Create tree • • // Create node containing B, and link bt 3 // up to subtrees B char. Tree. Ptr bt 3(new char. Tree); bt 3 ->insert('B'); bt 3 ->make. Left(bt 1); bt 1 bt 2 D E bt 3 ->make. Right(bt 2); // ** done creating left subtree

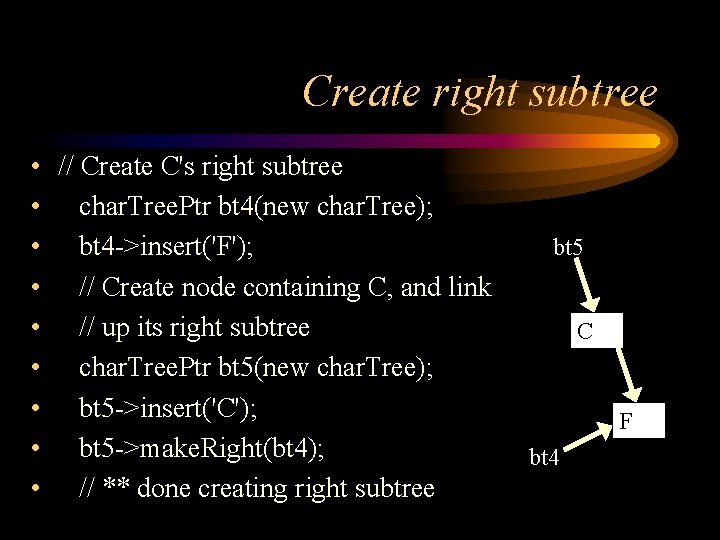
Create right subtree • // Create C's right subtree • char. Tree. Ptr bt 4(new char. Tree); • bt 4 ->insert('F'); • // Create node containing C, and link • // up its right subtree • char. Tree. Ptr bt 5(new char. Tree); • bt 5 ->insert('C'); • bt 5 ->make. Right(bt 4); • // ** done creating right subtree bt 5 C F bt 4

Create the root of the tree char. Tree. Ptr bt 6(new char. Tree); • bt 6 ->insert('A'); • bt 6 ->make. Left(bt 3); • bt 6 ->make. Right(bt 5); • • • // print out the root cout << "Root contains: " << bt 6 ->get. Data() << endl;

Final product bt 6 bt 3 bt 1 D A bt 5 B bt 2 E C bt 4 F

Print left and right subtrees • // print out root of left subtree • cout << "Left subtree root: " << bt 6 ->left()->get. Data() << endl; • • // print out root of right subtree cout << "Right subtree root: " << bt 6 ->right()->get. Data() << endl;

Print extreme child nodes • • cout << "Leftmost child is: " << bt 6 ->left()->get. Data() << endl; • • cout << "Rightmost child is: " << bt 6 ->right()->get. Data() << endl; • return 0; • }

Expression trees • enum eval. Node. Type { eval. Operator, eval. Operand }; • enum eval. Operator. Type { add, subtract, multiply, divide };

Class eval. Node • • • class eval. Node { public: eval. Node(double d); eval. Node(eval. Operator. Type op); eval. Node. Type get. Type() const; double get. Operand() const; eval. Operator. Type get. Operator() const; private: node. Type (op, opd) eval. Node. Type node. Type; double node. Operand; node. Operand (1, 2. . . ) eval. Operator. Type node. Operator; node. Operator (+-*/) };

Typedefs (creates the tree) • typedef eval. Node * eval. Node. Ptr; // Pointer to an eval. Node • // An eval. Tree is a Binary. Tree of pointers to eval. Nodes • typedef Binary. Tree < eval. Node. Ptr > eval. Tree; • typedef eval. Tree * eval. Tree. Ptr; // Pointer to an eval. Tree • double evaluate. Tree(eval. Tree. Ptr t);

Implementation file: polymorphism • eval. Node: : eval. Node(double d) • { node. Type = eval. Operand; • node. Operand = d; • } // creates operand node • eval. Node: : eval. Node(eval. Operator. Type op) • { node. Type = eval. Operator; • node. Operator = op; // creates operator node • }

get. Type(), get. Operand() • eval. Node. Type • eval. Node: : get. Type() const • { return node. Type; } // operator or operand • • • double eval. Node: : get. Operand() const { assert(node. Type == eval. Operand); return node. Operand; }

get. Operator() • • • eval. Operator. Type eval. Node: : get. Operator() const { assert(node. Type == eval. Operator); return node. Operator; }

evaluate. Tree() • double evaluate. Tree(eval. Tree. Ptr t) • { • assert(!t->is. Empty()); • eval. Node. Ptr root. Node. Ptr = t->get. Data(); • if (root. Node. Ptr->get. Type() == eval. Operand) • return root. Node. Ptr->get. Operand(); •

What kind of traversal is this? • else { • double left(evaluate. Tree(t->left())); • double right(evaluate. Tree(t->right())); • switch(root. Node. Ptr->get. Operator()) { • case add: return left + right; • case subtract: return left - right; • case multiply: return left * right; • case divide: • assert(right); // avoids div by 0 • return left / right; • } // switch • } // else • } // evaluate tree

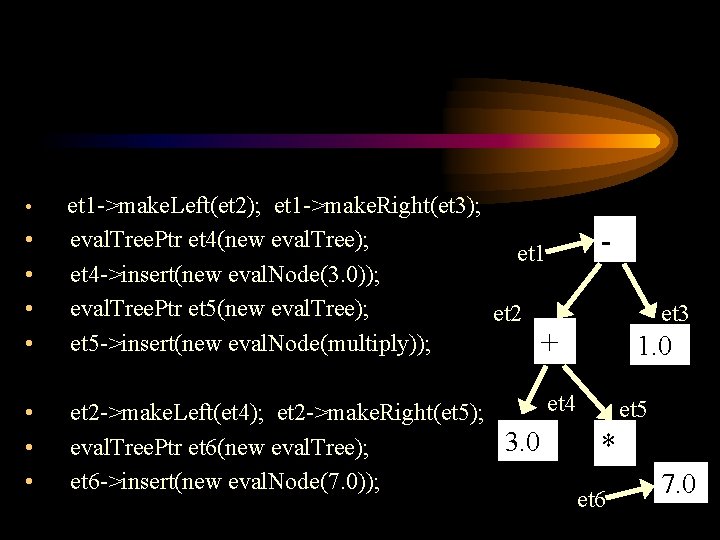
Using the expression tree • int main() • { • eval. Tree. Ptr et 1(new eval. Tree); • et 1 ->insert(new eval. Node(subtract)); • • et 1 - eval. Tree. Ptr et 2(new eval. Tree); et 2 ->insert(new eval. Node(add)); et 2 + eval. Tree. Ptr et 3(new eval. Tree); et 3 ->insert(new eval. Node(1. 0)); et 3 1. 0

• • et 1 ->make. Left(et 2); et 1 ->make. Right(et 3); eval. Tree. Ptr et 4(new eval. Tree); et 1 et 4 ->insert(new eval. Node(3. 0)); eval. Tree. Ptr et 5(new eval. Tree); et 2 et 5 ->insert(new eval. Node(multiply)); + • • • et 4 et 2 ->make. Left(et 4); et 2 ->make. Right(et 5); 3. 0 eval. Tree. Ptr et 6(new eval. Tree); et 6 ->insert(new eval. Node(7. 0)); • et 3 1. 0 et 5 * et 6 7. 0

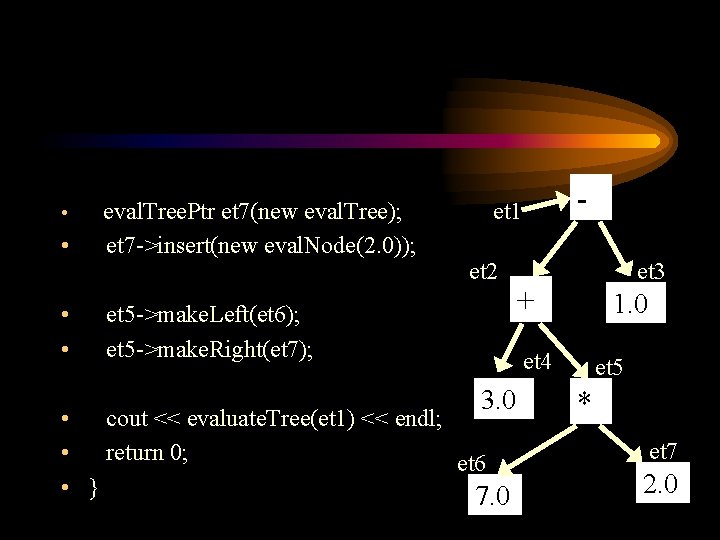
• eval. Tree. Ptr et 7(new eval. Tree); et 7 ->insert(new eval. Node(2. 0)); • • et 5 ->make. Left(et 6); et 5 ->make. Right(et 7); • - et 1 et 2 et 3 + 1. 0 et 4 3. 0 • cout << evaluate. Tree(et 1) << endl; • return 0; et 6 • } 7. 0 et 5 * et 7 2. 0

Methods of tree traversal • Must visit every element once • Must no miss any • Three basic types – preorder – inorder – postorder

Preorder traversal • if the tree is not empty • visit the root • pre. Order. Traverse(left child) • pre. Order. Traverse(right child)

Inorder traversal • if the tree is not empty • in. Order. Traverse(left child) • visit the root • in. Order. Traverse(right child)

Postorder traversal • if the tree is not empty • post. Order. Traverse(left child) • post. Order. Traverse(right child) • visit the root

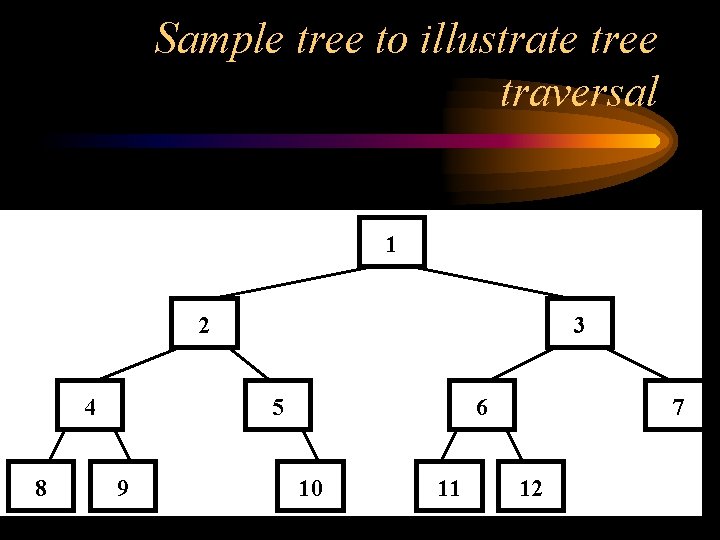
Sample tree to illustrate tree traversal 1 2 4 8 3 5 9 6 10 11 7 12

Tree after four nodes visited in preorder traversal 1 2 3 4 8 4 1 2 3 5 9 6 10 11 7 12

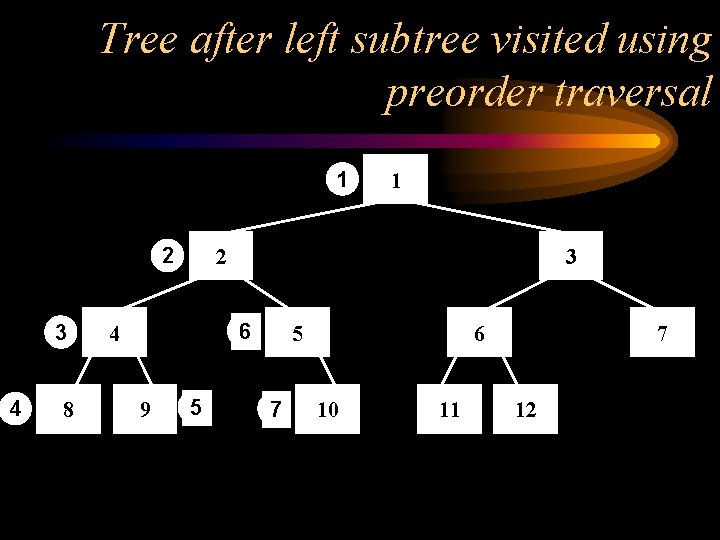
Tree after left subtree visited using preorder traversal 1 2 3 4 8 2 3 6 4 9 1 5 5 7 6 10 11 7 12

Tree after completed preorder traversal 1 2 3 4 8 8 2 6 4 9 1 5 9 5 7 10 10 3 12 6 11 12 11 7

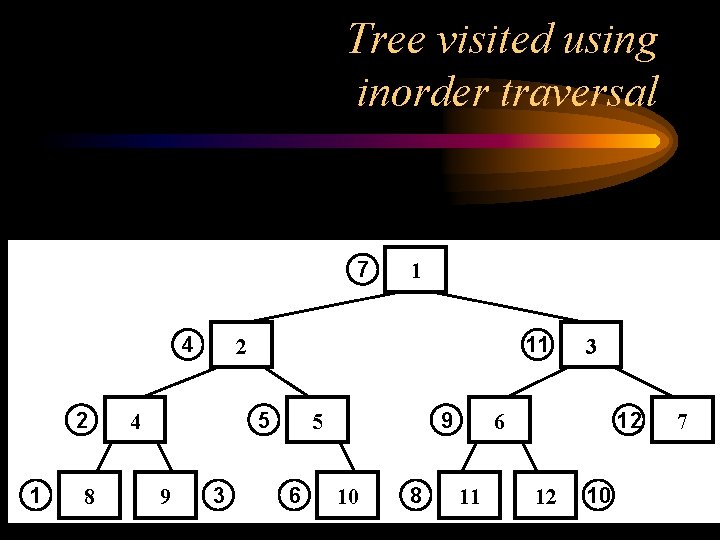
Tree visited using inorder traversal 7 4 2 1 8 11 2 5 4 9 1 3 9 5 6 10 8 3 12 6 11 12 10 7

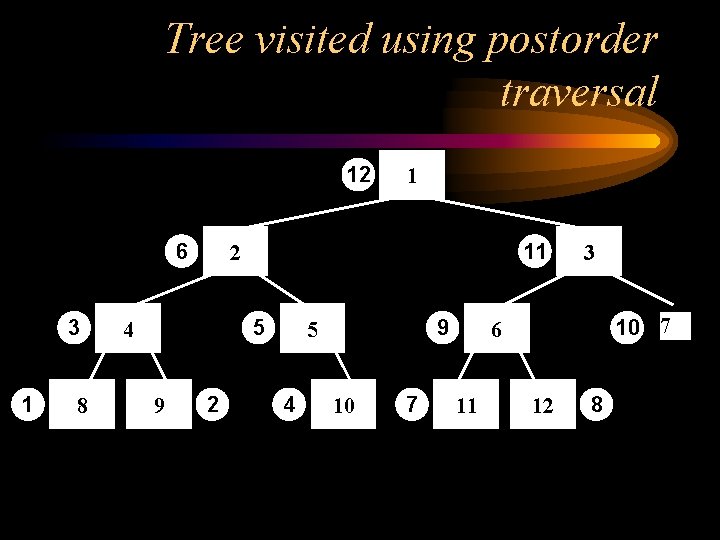
Tree visited using postorder traversal 12 6 3 1 8 11 2 5 4 9 1 2 9 5 4 10 7 3 10 7 6 11 12 8

Expression Tree for 3 + 7 *2 - 1 + 3 1 14

Binary tree traversals: preorder • • • typedef Binary. Tree < int > btint; typedef btint * btintp; void pre. Order. Traverse(btintp bt) { if (!bt->is. Empty()) { // if not empty // visit tree cout << bt->get. Data() << 't'; // traverse left child pre. Order. Traverse(bt->left()); // traverse right child pre. Order. Traverse(bt->right()); } }

Inorder traversal • void in. Order. Traverse(btintp bt) • { • if (!bt->is. Empty()) { • // traverse left child • in. Order. Traverse(bt->left()); • // visit tree • cout << bt->get. Data() << 't'; • // traverse right child • in. Order. Traverse(bt->right()); • }

Using function pointers • • We are used to sending pointers to variables Anything that has an address has a pointer Functions are addressable Therefore we can send functions into other functions by sending in their pointers • Similarly, we can call functions by dereferencing these pointers

Visit function • void visit(btintp bt) • { • cout << bt->get. Data() << 't'; • }

preorder traversal w/ * • • typedef Binary. Tree < int > btint; typedef btint * btintp; // pointer to integer binary tree void pre. Order. Traverse(btintp bt, void visit(btintp)) { if (!bt->is. Empty()) { • (* visit)(bt); // visit tree • // traverse left child • pre. Order. Traverse(bt->left(), visit); • // traverse right child • pre. Order. Traverse(bt->right(), visit); • }

Inorder traversal w/* • void in. Order. Traverse(btintp bt, void visit(btintp)) • { if (!bt->is. Empty()) { • // traverse left child • in. Order. Traverse(bt->left(), visit); • (* visit)(bt); // visit tree • //traverse right child • in. Order. Traverse(bt->right(), visit); • }