Chapter 7 Trees Trees w Trees are important

Chapter 7 Trees

Trees w Trees are important data structures in computer science. w Trees have interesting properties: n They usually are finite, but unbounded in size. n They sometimes contain other types within. n They are often polymorphic. n They may have differing “branching factors”. n They may have different kinds of leaf and branching nodes. w Lots of interesting things can be modeled as trees n lists (linear branching) n arithmetic expressions (see text) n parse trees (for languages) w In a lazy language it is possible to have infinite trees.

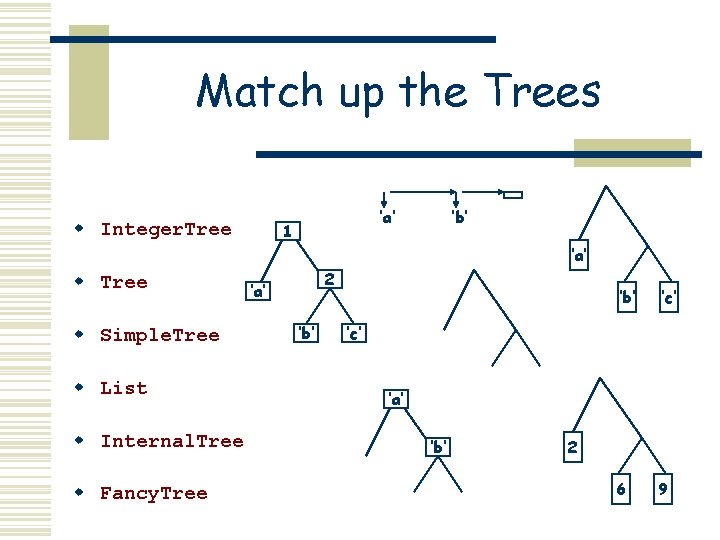
Examples data List a data = | Tree a = | Integer. Tree = | Simple. Tree = | Internal. Tree a = | data Fancy. Tree a b Nil Mk. List a (List a) Leaf a Branch (Tree a) Int. Leaf Integer Int. Branch Integer. Tree SLeaf SBranch Simple. Tree ILeaf IBranch a (Internal. Tree a) = FLeaf a | FBranch b (Fancy. Tree a b)

Match up the Trees w Integer. Tree ‘a’ 1 ‘b’ ‘a’ w Tree w Simple. Tree w List w Internal. Tree w Fancy. Tree 2 ‘a’ ‘b’ ‘c’ 6 9 ‘c’ ‘a’ ‘b’ 2

Functions on Trees w Transforming one kind of tree into another: map. Tree : : (a->b) -> Tree a -> Tree b map. Tree f (Leaf x) = Leaf (f x) map. Tree f (Branch t 1 t 2) = Branch (map. Tree f t 1) (map. Tree f t 2) w Collecting the items in a tree: fringe : : Tree a -> [a] fringe (Leaf x) = [x] fringe (Branch t 1 t 2) = fringe t 1 ++ fringe t 2 w What kind of information is lost using fringe?

More Functions on Trees tree. Size : : Tree a -> Integer tree. Size (Leaf x) = 1 tree. Size (Branch t 1 t 2) = tree. Size t 1 + tree. Size t 2 tree. Height : : Tree a -> Integer tree. Height (Leaf x) = 0 tree. Height (Branch t 1 t 2) = 1 + max (tree. Height t 1) (tree. Height t 2)

Capture the Pattern of Recursion Many of our functions on trees have similar structure. Can we apply the abstraction principle? Yes we can: fold. Tree : : (a -> a) -> (b -> fold. Tree combine leaf. Fn (Leaf x) = fold. Tree combine leaf. Fn (Branch t 1 combine (fold. Tree combine a) -> Tree b -> a leaf. Fn x t 2) = leaf. Fn t 1) leaf. Fn t 2)

Using fold. Tree With fold. Tree we can redefine the previous functions as: map. Tree f = fold. Tree Branch fun where fun x = Leaf (f x) fringe = fold. Tree (++) fun where fun x = [x] tree. Size = fold. Tree (+) (const 1) tree. Height = fold. Tree fun (const 0) where fun x y = 1 + max x y

Arithmetic Expressons data Expr = | | C Float Add Expr Sub Expr Mul Expr Div Expr Expr Or, using infix constructor names: data Expr = | | C Float Expr : + Expr : * Expr : / Expr Infix constructors begin with a colon (: ) , whereas ordinary constructor functions begin with an upper-case character.

Example e 1 = (C 10 : + (C 8 : / C 2)) : * (C 7 : - C 4) evaluate evaluate (C x) (e 1 : + (e 1 : * (e 1 : / : : = e 2) = Main> evaluate e 1 42. 0 Expr -> Float x evaluate e 1 + evaluate e 1 * evaluate e 1 / evaluate e 2 e 2