How Computers Think Binary Decimal and Hexadecimal For

How Computers Think: Binary, Decimal and Hexadecimal For NYSCPT Summer Institute, NYU 8 -16 -02 Andrew O’Neill Columbia University

Introduction ● ● Why do people and computers think in different ways? How do people think about numbers? Where did these ideas come from? ● How do computers use numbers? ● How can we speak the computer's language? ● Two mysteries solved - you too can count to 1000 on two hands!

History of (human) numbers ● ● 1 st Mystery: The Mesopotamians used a base-60 number system, from which we still use minutes, seconds and degrees. Greeks/Romans use base-10, in a different form. . . 12 3 4 5 6 7 8 9 I II IV V VI VIII IX X, L, C, D, M We have 10 fingers, so this makes sense, right?

● Refined by introduction of zero and the place system - 'decimal' as we know it 0123456789 10, 1000. . . – Allows us to deal with very large numbers, and fractions. – Proven successful over time.

How Computers Count ● Computers are logical electronic devices – All data is just a combination of two states 'on' and 'off'. ● ● These states are called “Binary dig. ITs” (BITS), which can only take a value of 1 or 0. Use the place system just like decimal 1 represents decimal 'one', 10 represents decimal 'two'. . .

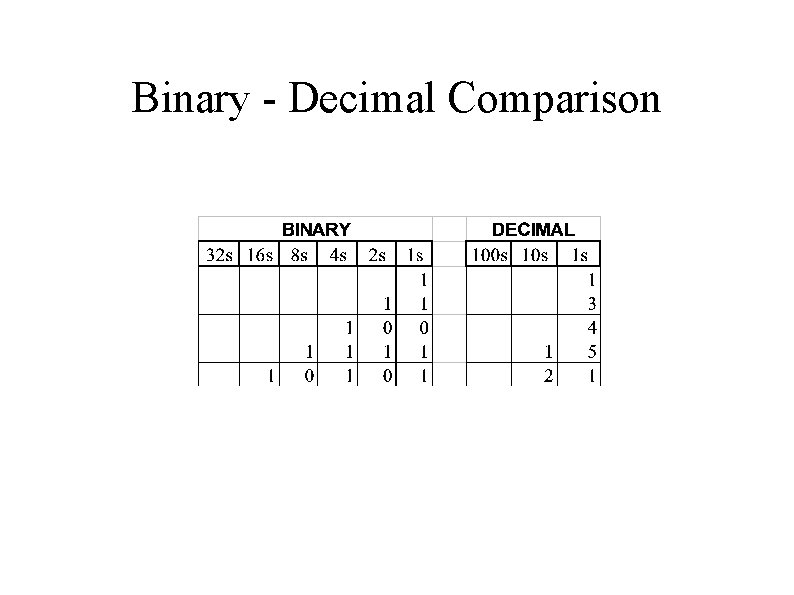
Binary - Decimal Comparison

● Maximum different values we can represent with n bits is 2 n. ● One BYTE = 8 BITS ● One BYTE holds 2 n = 256 different values. ● ● ASCII is a code for most characters between 0 & 255 Oh yeah, computers typically start counting at zero!

ASCII Codes in Decimal 000 001 002 003 004 008 009 010 011 012 016 017 018 019 020 024 025 026 027 028 032 033 ! 034 " 035 # 036 $ 037 % 038 & 039 ' 040 ( 041 ) 042 * 043 + 044 , 045 - 046. 047 / 048 0 049 1 050 2 051 3 052 4 053 5 054 6 055 7 056 8 057 9 058 : 059 ; 060 < 061 = 062 > 063 ? 064 @ 065 A 066 B 067 C 068 D 069 E 070 F 071 G 072 H 073 I 074 J 075 K 076 L 077 M 078 N 079 O 080 P 081 Q 082 R 083 S 084 T 085 U 086 V 087 W 088 X 089 Y 090 Z 091 [ 092 093 ] 094 ^ 095 _ 096 ` 097 a 098 b 099 c 100 d 101 e 102 f 103 g 104 h 105 i 106 j 107 k 108 l 109 m 110 n 111 o 112 p 113 q 114 r 115 s 116 t 117 u 118 v 119 w 120 x 121 y 122 z 123 { 124 | 125 } 126 ~ 127. . . 128 to 255 used for non-latin characters. . . 005 013 021 029 006 014 022 030 007 015 023 031

Hexadecimal ● Base 16 ● Need more symbols than 0, 1, . . . , 9 ● 123456789 ABCDE ● "Ox" notation Ox 15 = 16 in decimal (1*16 + 5 = 21)

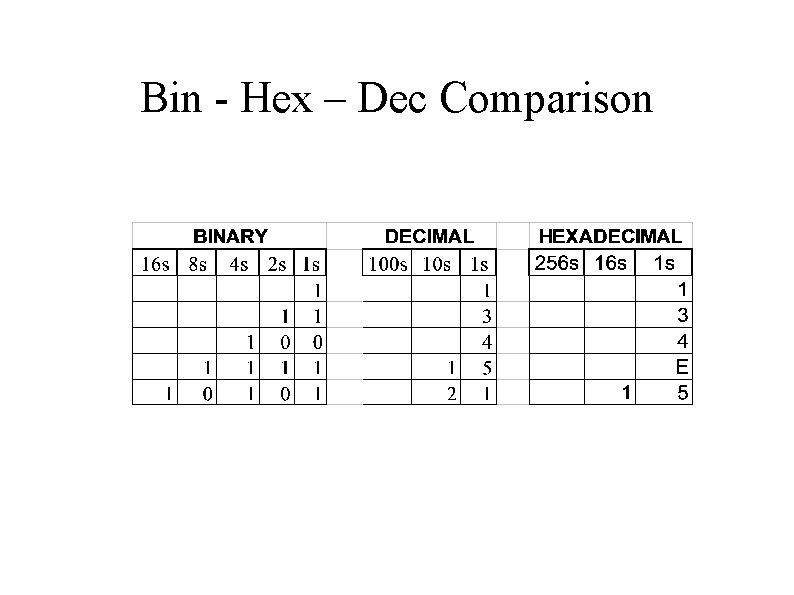
Bin - Hex – Dec Comparison

So Why Hex? ● Base 16, or 24 – Holds as much information as 4 bits – E. g. 0 x. E is equivalent to binary 1111 ● 1 byte can be represented by 2 hex characters ● Saves writing 8 bits! – ● Saves space on small screens Useful in displaying computer information

Communicating With Our Electronics ● ● Our electronics board has 4 inputs We need to tell it which ones to look for coincidences on

Calculator Demo Counting to 1000

So why base 60? ● Mesopotamians had cool numbers…

Theory #1 60 is the smallest number divisible by 2, 3, 4, and 5. ● Theory #2 ● Mixing of two civilizations, one with base 5, one with base 12…

Theory #3 Three-parts to each finger on right hand = 12 ● Point to one of these 12 parts with one of 5 fingers on left hand ● 5 x 12 = 60 ● … Theory # … ● Astronomical, geometrical, yada

The Real Reason ● There are 0 x 3 C reasons why the ancient civilizations used base-60!!!