Binary Hex The number systems of Computer Science

Binary & Hex The number systems of Computer Science

What you will learn Decimal Binary Hexadecimal Arithmetic Converting between number bases Counting 2’s Compliment

Number Systems Prehistory Unary, or marks: / /////// = 7 /////// + ////// = /////// Babylonian (Mesopotamia) around 2000 BC Used 60 numerical symbols – sexadecimal. Used to measure time 5; 25, 30 = 5 hr 25 min 30 secs. Was positional based by had no concept of zero. 5, 4560 = 5 x 60 + 45 x 1 = 34510 Roman Numerals: (non positional, no concept of zero) VII + V = VVII = XII MCMXCIX = 1999 MCMXCVIIII = 1999 MCMLXXXXVIIII = 1999 MDCCCCLXXXXVIIII = 1999

Quote from Pierre Simon Laplace “The ingenious method of expressing every possible number using a set of ten symbols (each symbol having a place value and an absolute value) emerged in India. The idea seems so simple nowadays that its significance and profound importance is no longer appreciated. Its simplicity lies in the way it facilitated calculation and placed arithmetic foremost amongst useful inventions. the importance of this invention is more readily appreciated when one considers that it was beyond the two greatest men of Antiquity, Archimedes and Apollonius. “

Arabic/Indian Numerals (Decimal) Better, Arabic/Indian based Numerals: 7 + 5 = 12 = 1 x 10 + 2 345 is really n n 3 x 100 + 4 x 10 + 5 x 1 3 x 102 + 4 x 101 + 5 x 100 3 is the most significant symbol (carries the most weight) 5 is the least significant symbol (carries the least weight) Digits (or symbols) allowed: 0 -9 Base (or radix): 10

• Try multiplication in (non-positional) Roman numerals(!): XXXIII (33 in decimal) XII (12 in decimal) ----XXXIII CCCXXX -----CCCXXXXXIIIIII CCCLXXXXVI CCCXCVI = 396 • The Babylonians wouldn’t have had this problem.

• There are many ways to “represent” a number • Representation does not affect computation result LIX + XXXIII = LXXXXII (Roman) 59 + 33 = 92 (Decimal) • Representation affects difficulty of computing results • No concept of “Zero” • Computers need a representation that works with fast electronic circuits

What is the base ? The decimal numbering system is also known as base 10. The values of the positions are calculated by taking 10 to some power. l Why is the base 10 for decimal numbers ? l Because we use 10 digits. The digits 0 through 9.

Main Memory Original computers used holes/no hole to represent two state, 1/0. Modern computers use transistor on/off translates to values 1/0 Requires use of Binary number system

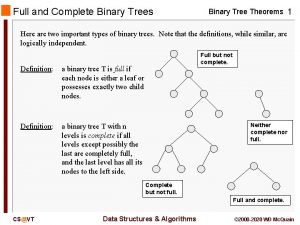
Binary: positional numbers work great with 2 -state devices • Digits (symbols) allowed: 0, 1 • Binary Digits, or bits • Base (radix): 2 • 10012 is really • 1 x 2 3 + 0 x 2 2 + 0 X 2 1 + 1 X 2 0 • 910 • 110002 is really • ? • Computers usually multiply Arabic numerals by converting to binary, multiplying and converting back for display

Counting in Binary l Binary 0 1 10 11 100 101 110 111 l Decimal equivalent 0 1 2 3 4 5 6 7

Decimal to Binary • Divide decimal value by 2 until the value is 0 E. g. 47 /2 23/2 11/2 5/2 2/2 1/2 = = = 23 Remainder 1 11 Remainder 1 5 Remainder 1 2 Remainder 1 1 Remainder 0 0 Remainder 1 Read from the bottom up Ans: 101111

Binary to Decimal 1 0 0 0 1 2 6 2 5 2 4 23 2 2 21 2 0 20 = 1 21 = 2 22 = 4 23 = 8 24 = 16 25 = 32 26 = 64 1 X 20 = 1 0 X 21 = 0 0 X 22 = 0 0 X 23 = 0 0 X 24 = 0 0 X 25 = 0 1 X 26 = 64 65

Binary to Decimal (alternative) Converting the binary 100101 to 37 Multiply running total by two, add in next digit. Repeat for all digits.

Some buzz words • • Single Binary Digit =Bit 4 bits = nibble 8 bits = byte 16 bits = word 32 bits = longword 2 nibbles = 1 byte 2 bytes = 1 word The word size depends on the processor used, above is shown the word size for the 68000

Addition of Binary Numbers l Examples: 1001 +0110 1111 0001 +1001 1010 Carry a one 1100 +0101 1 0001

Addition (large numbers) l Example showing larger numbers: 1010 0011 1011 0001 + 0111 0100 0001 1 0001 0111 1100 1010

Working with large numbers 0101 0000 1001 0111 Humans can’t work well with binary numbers. We will make errors. l Shorthand for binary that’s easier for us to work with - Hexadecimal l

Hexadecimal Binary 0 1 0 0 1 1 1 Hex 5 Written: 509716 0 9 7

What is Hexadecimal really ? Binary 0 1 0 0 1 1 1 Hex 5 0 9 7 A number expressed in base 16. It’s easy to convert binary to hex and hex to binary because 16 is 24.

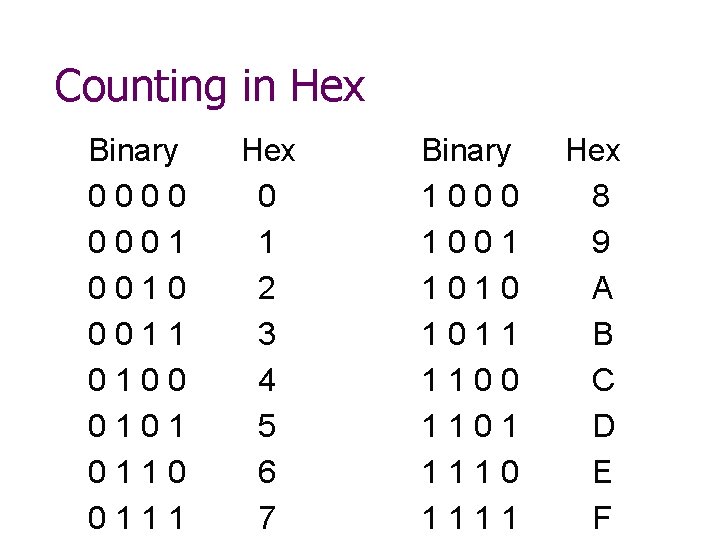
Counting in Hex Binary 0000 0001 0010 0011 0100 0101 0110 0111 Hex 0 1 2 3 4 5 6 7 Binary 1000 1001 1010 1011 1100 1101 1110 1111 Hex 8 9 A B C D E F

Decimal to Hex Repeat dividing by 16 and noting the remainder until the quotient = 0 E. g. 54401 d to Hex 54401/16 = 3400 Remainder 1 3400/16 = 212 Remainder 8 212/16 = 16 Remainder 4 13/16 = 0 Remainder 13 Remainders are expressed Hex numbers Answer: $D 481

Hex to Decimal Write out the 1 st 16 numbers Same as for binary to decimal E. g. F 9 E 116 1 x 160 =1 Ex 161 =14 x 16 = 224 9 x 162 =9 x 256 = 2304 Fx 163 =15 x 4096= 61440 = 63969

Another Binary to Hex Conversion Binary 0 1 1 1 0 0 1 1 1 Hex 7 C 3 F 16 7 C 3 F

Binary Coding Schemes To represent characters we use Binary Coding Schemes Two of the most popular are n n ASCII (American Standard Code for Information Interchange EBCDIC (Extended Binary Coded Decimal Interchange Code) Here are some ASCII codes n n n n CHARACTER ASCII A 01000001 – 41 in hex B 01000010 - 42 in hex C 01000011 - 43 in hex D 0100 - 44 in hex BELL 00000111 – 7 in hex ESC 00011101 – 1 B in hex

Binary Coded Decimal (BCD) Each digit is converted individually to it’s binary equivalent 2634 = 0010 0110 0011 0100 3825 = 0011 1000 0010 0101 Disadvantages are that arithmetic is more complicated and storage is inefficent. Used only in simple device where memory is not a problem e. g. Calculators, clocks, etc.

Negative Integers Most humans precede number with “-” (e. g. , -2000) n Accountants, however, use parentheses: (2000) Sign-magnitude Example: -1000 in hex? n n 100010 = 3 x 162 + e x 161 + 8 x 160 -3 E 816

2’s Compliment Used for negative binary numbers Procedure: Invert all the bits: 0 becomes 1 and 1 becomes 0 Add 1 E. g. To get – 1 110 = 000000012 Invert all bits 11111110 Add 1 1111 Ans: -110 = 11112

2’s Compliment Using the TC notation, the Most significant indicates the sign. 1 means a negative number With 8 bits, can represent signed numbers in the range: +127 01111111 -1 1111 0 0000 -128 10000000 With N bits, can represent signed numbers in the range: (2 N-1)-1 0 -(2 N-1) TC is widely used because it is easy to manipulate. The sign bit is treated the same as the others

2 s Compliment Clock Stepping clockwise increases the binary number Stepping anti-clockwise decreases the binary number Notice how when we add one to a negative number it’s values move closer to zero

Addition & Subtraction Addition of TC’s numbers same as normal binary addition Subtraction of TC’s numbers can use either A-B or A + TC(B) E. g. 01112 – 00112 = ? ? ? Change second number to TC 0111 1101+ 0100 Answer: 01112 – 00112 = 01002

Decimal fractions to binary More info on p 158 Clements. Question: Convert 0. 6250 (decimal) to a binary fraction 0. 3125 x 2 = 0. 6250 yielding 0 0. 625 x 2 = 1. 2500 yielding 1 0. 25 = 0. 5000 yielding 0 0. 5 x 2 = 1. 0000 yielding 1 Ans: 0. 0101

Binary to Decimal fractions More info on p 158 Clements.

Summary Decimal Binary Hexadecimal Arithmetic Converting between number bases Counting Coding schemes 2’s Compliment