Number Systems Decimal Binary and Hexadecimal 1 Positional

Number Systems Decimal, Binary, and Hexadecimal 1

Positional Notation 2

Positional Notation A positive number N can be written as: Where: 3

Definitions Where: . = radix point r = radix or base of number system n = number of integer digits to the left of radix point m = number of fractional digits to the right of radix point ai = integer digit i aj = fractional digit j an-1 = most significant digit a -m = least significant digit 4

Examples (1920)10 1920 n n Base 10 or decimal number Unless otherwise noted, assume base 10 (10010101)2 100101012 n Base 2 or binary number (95)16 9516 n Base 16 or Hex number 5

Online HW Assignments (1920)10 1920 n Base 10 or decimal number (10010101)2 %10010101 n Base 2 or binary number (95)16 $95 n Base 16 or Hex number 6

Polynomial Notation A positive number N can also be written as: Example: 7

Common Number Systems 8

Decimal Number System Radix or Base 10 Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Example: 104510 First 17 positive integers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 9

Binary Number System Radix or Base 2 Digits: 0, 1 Example: 10101102 First 17 positive integers 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1 011, 1100, 1101, 1110, 1111, 10000 10

Hexadecimal Number System Radix or Base 16 Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Example: EF 5616 First 17 positive integers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10 11

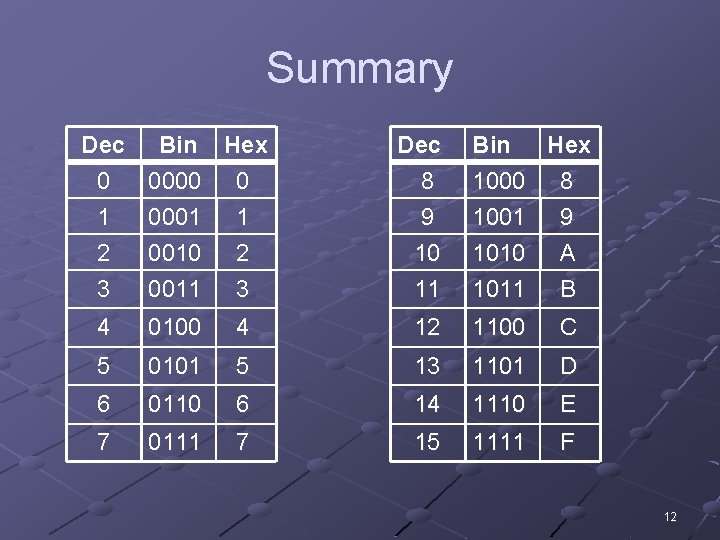
Summary Dec Bin Hex 0 0000 0 1 0001 1 2 0010 2 3 0011 3 Dec 8 9 10 11 Bin Hex 1000 8 1001 9 1010 A 1011 B 4 0100 4 12 1100 C 5 0101 5 13 1101 D 6 0110 6 14 1110 E 7 0111 7 15 1111 F 12

Decimal Arithmetic Addition Subtraction Multiplication Division 13

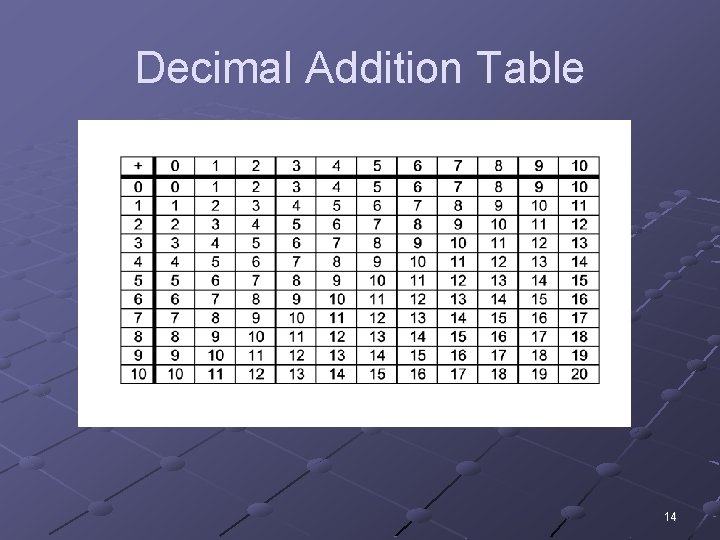
Decimal Addition Table 14

Example Add the following decimal numbers 199 + 73 15

Solution Add the following decimal numbers 1 1 199 + 73 27 2 16

Solution Subtract the following decimal numbers 123 - 77 17

Solution Subtract the following decimal numbers 1 123 - 77 6 18

Solution Subtract the following decimal numbers 1 1 113 - 77 46 19

Solution Subtract the following decimal numbers 1 1 013 - 77 04 6 20

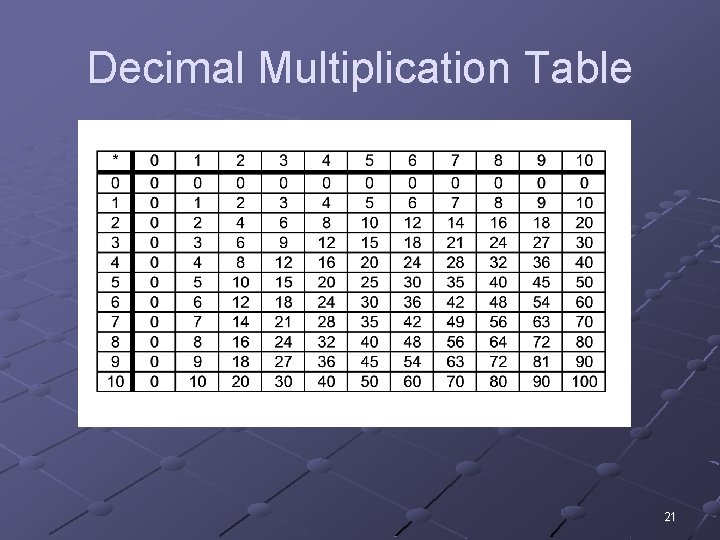
Decimal Multiplication Table 21

Example Multiply the following decimal numbers 72 x 23 22

Solution Multiply the following decimal numbers 72 x 23 216 1440 1656 Multiplicand Multiplier Partial Products Product 23

Example Divide the following decimal numbers 3 23 24

Example Divide the following decimal numbers 07 Divisor 3 23 0 23 21 2 Quotient Dividend Remainder 25

Binary Arithmetic 26

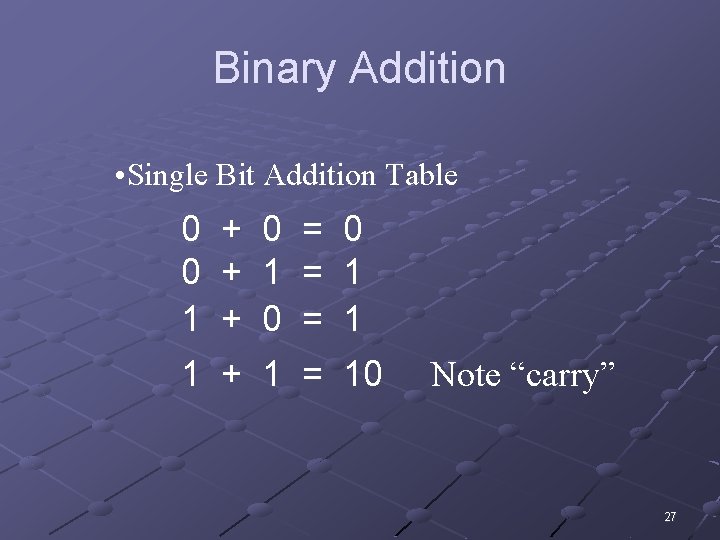
Binary Addition • Single Bit Addition Table 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 Note “carry” 27

Example Add the following binary numbers 1101 +0 1 1 1 28

Solution: Add the following binary numbers 1 1 1101 +0 1 10100 29

Binary Subtraction • Single Bit Subtraction Table 0 - 0 = 0 1 - 0 = 1 1 - 1 = 0 0 - 1 = 1 with a “borrow” 30

Example Subtract the following binary numbers 1101 -0111 31

Solution: Subtract the following binary numbers 1 1 1 0 10 101 -0111 0110 32

Collaborative Learning methodology in which students are not only responsible for their own learning but for the learning of other members of the group. 33

Think - Pair - Share (TPS) Quizzes Think – Pair – Share n n Think individually for one time units Pair with partner for two time units Share with group for one and half time units Report results 34

TPS Quiz THINK One Unit (e. g. 30 Seconds) 35

TPS Quiz PAIR Two Units (e. g. 60 Seconds) 36

TPS Quiz SHARE 1. 5 units (e. g. 45 Seconds) 37

TPS QUIZ Report 38

TPS Quiz #1 -2 -3 39

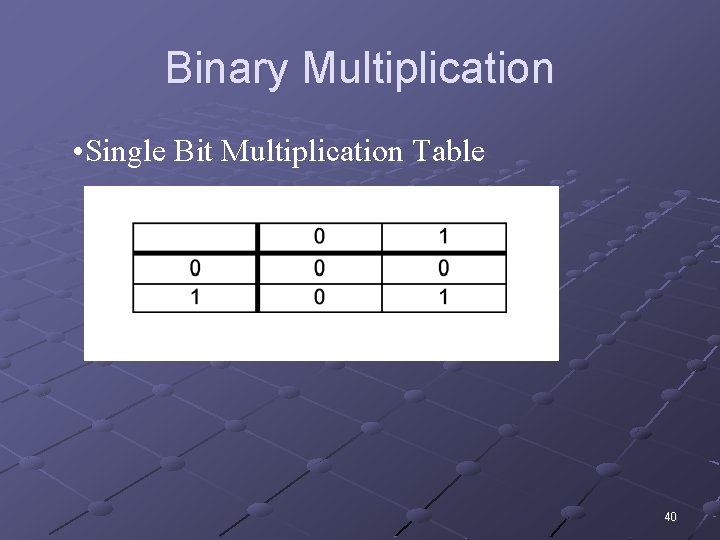
Binary Multiplication • Single Bit Multiplication Table 40

Binary Multiplication • Single Bit Multiplication Table 0 x 0 = 0 0 x 1 = 0 1 x 0 = 0 1 x 1 = 1 41

Example Multiply the following binary numbers 1101 x 0111 42

Solution Multiply the following binary numbers 1101 x 0111 110100 0000000 1011011 Partial Products 43

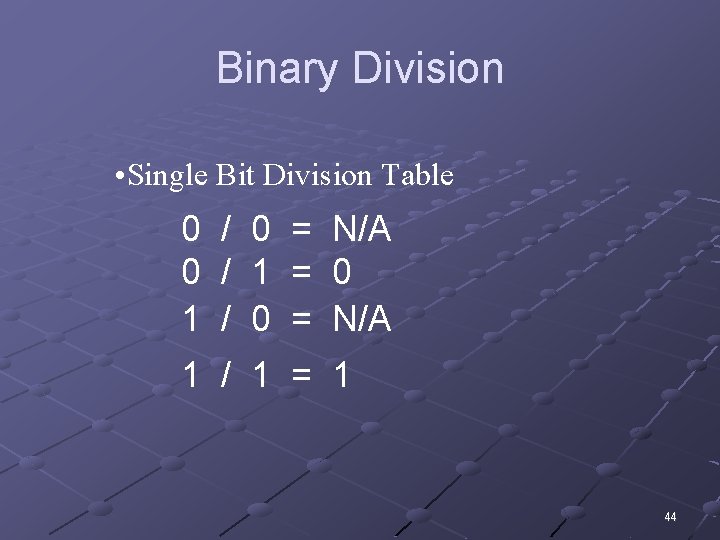
Binary Division • Single Bit Division Table 0 / 0 = N/A 0 / 1 = 0 1 / 0 = N/A 1 / 1 = 1 44

Example Divide the following binary numbers 111 1101 45

Solution Divide the following binary numbers Quotient 0 0 01 Divisor 111 1101 Dividend 0 11 00 110 000 1101 110 Remainder 46

Hexadecimal Arithmetic 47

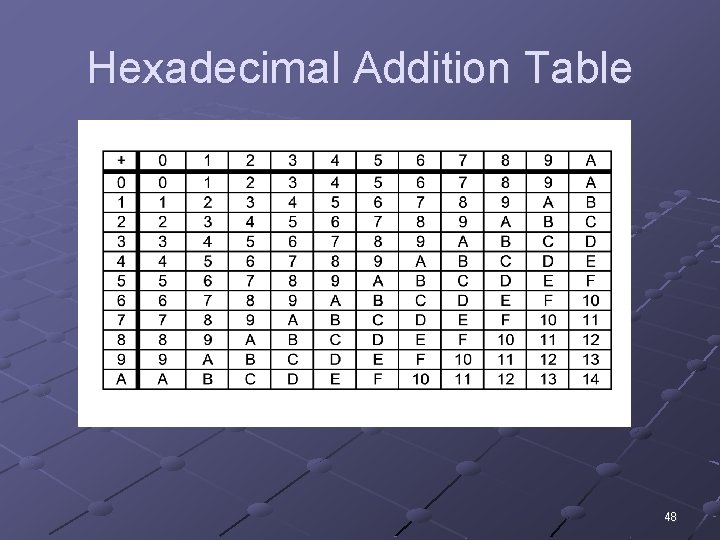
Hexadecimal Addition Table 48

Example Add the following hexadecimal numbers AF + 1 B 49

Solution Add the following hexadecimal numbers 1 AF + 1 B CA 50

Example Subtract the following hexadecimal numbers AB - 1 D 51

Solution Subtract the following hexadecimal numbers AB - 1 D 9 1 AB - 1 D E 9 1 AB - 1 D 8 E 10 -D+B=3+B=E 52

TPS Quiz #4 -5 -6 53

Conversion Methods 54

Series Substitution Expand number in original base using 55

Binary to Decimal Example – Convert to Base 10 56

Hex to Decimal Example – Convert to Base 10 57

Radix Divide Method Convert N in base A to base B Note: N can be expanded in base B using OR We know B, but how do we find the bi’s 58

Radix Divide Method We can divide N by B to find Remainder Quotient 59

Radix Divide Method So is the remainder of We can repeat the division to find Or is the remainder of 60

Radix Divide Method We can repeat the division until The remainder is 61

Example Decimal to Binary Conversion 110000111002 62

Example Decimal to Hex Conversion 63

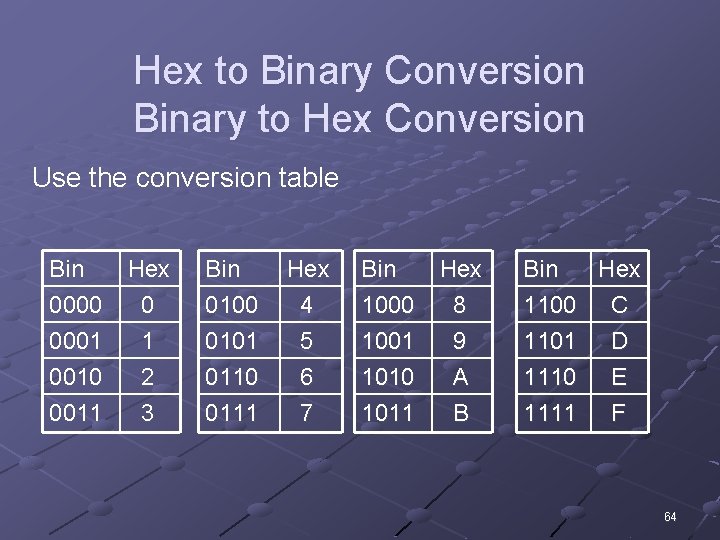
Hex to Binary Conversion Binary to Hex Conversion Use the conversion table Bin 0000 0001 0010 Hex 0 1 2 Bin 0100 0101 0110 Hex 4 5 6 Bin 1000 1001 1010 Hex 8 9 A 0011 3 0111 7 1011 B Bin Hex 1100 C 1101 D 1110 E 1111 F 64

Binary to Hex Conversion 1. Divide binary number into 4 -bit groups 01 1 0 0 1 1 1 0 0 Pad with 0’s if unsigned number 2. Substitute hex digit for each group Pad with sign bit if signed number 61 C 16 65

Hex to Binary Conversion Convert each hex digit into equivalent binary number 1 E 3 F 16 0001111112 66

TIP Binary to decimal conversions 1. Convert binary to hex 2. Convert hex to decimal Example: Convert 10102 to Dec (assume unsigned numbers) 10102 $AA = 16*10+10=170 Check 27+25+23+21=128+32+8+2=170 67

TPS Quiz #7 -8 -9 68

Signed Numbers 69

Signed Numbers Two methods: n Signed-magnitude Use one digit (character) to represent the sign n Example: + = positive, - = negative Remaining bits are used to represent the magnitude Ex: +109 or -234 Digital arithmetic circuitry would be large and slow. n Signed-complement Use the radix complement of N to represent –N This method is used in digital logic design 70

Radix Complements 71

Definition Radix Complements Where = Radix Complement of N = Original Number, N r n = radix or base = number of digits 72

Definition Note: Or, N added to its complement is equal to rn But this is just 0, if we ignore the Most Significant Digit (MSD) 73

Radix Complements Two’s Complement Ten’s Complement 74

Radix Complements 16’s Complement 75

Example Calculate the 10’s complement of N= 3 Let n=1 76

Example Calculate the two’s complement of N= 00100110. Let n=8 77

Properties Or, the two’s complement of N is the same as -N * Ignoring the most significant digit which will always be 1 78

Properties The two’s complement of the two’s complement of N is just N. Recall , SO 79

Example Let’s find Throw this away So, 80

Definition Diminished Radix Complements where r = radix or base n = number of digits Note: ai = digit to convert 81

One’s Complement One’s complement (Diminished) So Or, But, 1 -0=1 and 1 -1=0, or to calculate the 1’s complement of a binary number just “flip” or complement each bit of the original binary number. E. g. 0 1 and 1 0 Example: 01010100100 10101011011 82

Two’s Complement We have, But this is just Or, 83

Two’s Complement Two’s complement calculation method #2 n To calculate the 2’s complement just calculate the 1’s complement and add 1. Example: With N= 001001102 , we found Let’s calculate the 2’s complement of N using its 1’s complement 84

Two’s Complement Two’s complement calculation method #3 n Leave all of the least significant 0’s and first 1 unchanged and then “flip” or complement the bits for all other digits. Example: Calculate the 2’s complement of Leave these bits alone We have Complement these bits 85

Summary Two’s complement calculations Method 1 Method 2 Method 3 Leave all of the least significant 0’s and first 1 unchanged and then “flip” or complement the bits for all other digits 86

16’s Complement The 16’s complement of a 16 bit (or 4 digit) hexadecimal number is: Example, let N= $B 2 CE 87

Signed Binary Numbers 88

Signed Binary Numbers Use 2’s complement of N to represent –N n Signed binary 2’s complement If MSB of N is 0, N is positive If MSB of N is 1, N is negative Range of signed binary numbers is: Range of unsigned binary numbers is: 89

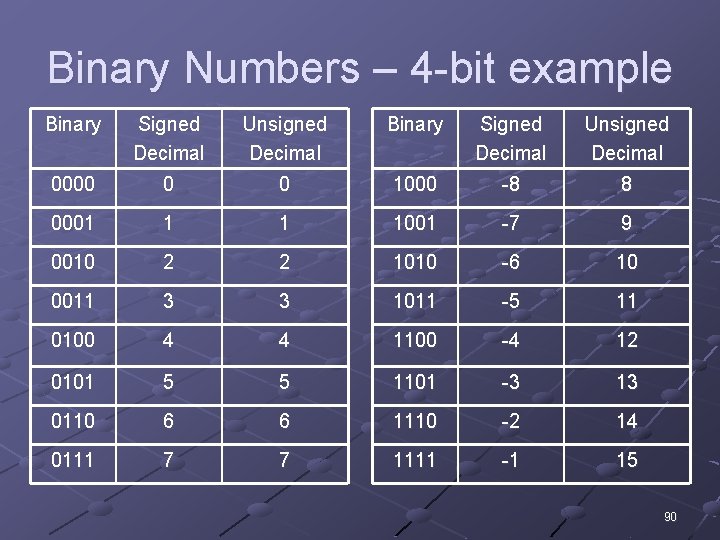
Binary Numbers – 4 -bit example Binary Signed Decimal Unsigned Decimal 0000 0 0 1000 -8 8 0001 1 1 1001 -7 9 0010 2 2 1010 -6 10 0011 3 3 1011 -5 11 0100 4 4 1100 -4 12 0101 5 5 1101 -3 13 0110 6 6 1110 -2 14 0111 7 7 1111 -1 15 90

Procedure to Convert 2’s complement to decimal To convert a 2’s complement number (or signed binary) into its decimal equivalent. We first check the MSB n If MSB=0, the number is positive and we a) calculate its decimal equivalent as before. n If MSB=1, the number is negative, we a) calculate its 2’s complement to obtain its magnitude b) calculate its decimal equivalent as before c) Add the minus sign (-) to the decimal result to indicate it is negative. 91

Example Assume signed 2’s complement numbers, let N=4, What is the decimal equivalent of Since MSB=1, this is a negative number. We need to calculate its 2’s complement to determine its magnitude Let’s use all three methods to calculate 92

Example Method 1 Method 2 Method 3 Leave LSB 0’s and first 1 alone, flip all other bits. 93

Example So, as a signed 2’s complement number 94

Example Assume signed 2’s complement numbers, let n=8, What is the decimal equivalent of Since MSB=1, this is a negative number, we need to calculate its 2’s complement to determine its magnitude So, 95

Very Important!!! – Unless otherwise stated assume signed-complement numbers for all problems, quizzes, HW’s, etc. 96

Binary Subtraction 97

Binary Subtraction Note: n n A – (+B) = A + (-B) A – (-B) = A + (-(-B))= A + (+B) In other words, we can “subtract” B from A by “adding” –B to A. However, -B is just the 2’s complement of B, so to perform binary subtraction, we 1. Calculate the 2’s complement of B 2. Add A + (-B) 98

Binary Subtraction - Example Let n=4, A=01002 (410), and B=00102 (210) Let’s find A+B, A-B and B-A A+B 0 1 0 0 (4)10 + 0 0 1 0 (2)10 0110 6 99

Binary Subtraction - Example A-B A+ (-B) 0 1 0 0 (4)10 - 0 0 1 0 (2)10 0 1 0 0 (4)10 + 1 1 1 0 (-2)10 10 0 1 0 2 “Throw this bit” away since n=4 100

Binary Subtraction - Example B-A B + (-A) 0 0 1 0 (2)10 - 0 1 0 0 (4)10 0 0 1 0 (2)10 + 1 1 0 0 (-4)10 1110 -2 1 1 1 02 = - 0 0 1 02 = -210 101

Sign Extension 102

Sign Extension Assume a signed 2’s complement system Let A = 0101 (4 bits) and B=010 (3 bits) What is A+B? n n To add these two values we need A and B to be of the same bit width. Do we truncate A to 3 bits or add an additional bit to B? 103

Sign Extension A = 0101 and B=010 Can’t truncate A!! Why? n n A: 0101 But 0101 <> 101 in a signed system 0101 = +5 101 = -3 104

Sign Extension Must “sign extend” B, so B becomes 010 0010 Note: Value of B remains the same So 0101 (5) +0010 (2) Sign bit is extended -------0111 (7) 105

Sign Extension What about negative numbers? Let A=0101 (+5) and B=100 (-4) Now B = 100 1100 0101 +1100 ------10001 Sign bit is extended (+5) (-4) (1) Throw away 106

TPS Quiz # 10 -11 -12 107

Computer Codes 108

Binary Coded Decimals (BCDs) Dec Use a 4 -bit code to represent each decimal digit. Example: 123410 n n %0001001000110100 In hex, $1234 Note: As a signed decimal, $1234 is not equal to 123410 but 466010 0 1 2 Bin 0000 0001 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 109

ASCII American Standard Code for Information Interchange 7 -bit character code used in computer applications. (8 -bit code called extended ASCII) See Table 1. 11 For Example, n n n ‘ 1’ = %0110001 = $31 ‘A’ = %1000001 = $41 ‘a’ = %1100001 = $61 110

Important!! The logic designer determines what a binary number represents? For example, n What is “ 10010111” in the following connotations? As a unsigned binary = 151 As a signed binary = -104 As a BCD (Binary Coded Decimal) = 97 As an ASCI Character = “—” Em dash 111

Fractional Numbers 112

Fractional Numbers Recall 20=1, 21=2, 22=4, …. But, we can also go the other way n 2 -1=0. 5, 2 -2=0. 25, 2 -3=0. 125, 2 -4=0. 0625, … In general, we have 2 -n=1/2 n So, for example, to represent n n 2. 5 = 10. 102 = %1010 and 5. 25 = 101. 012 = %10101 Check: 2+0+0. 5+0=2. 5 Check: 4+0+1+0+0. 25=5. 25 113

Fractional Numbers We have n 2. 5 = %10. 10 and 5. 25 = %101. 01 As 8 bit numbers, these become n %000010. 10 and %000101. 01 Now, we really DON’T have a way to represent the binary point in our numbers, so we have to remember where it is located. So really, we have 2. 5 = %00001010 = $0 A 5. 25 = %00010101 = $15 And we remember that we are using 2 bits for the fractional part. 114

Fractional Numbers Let’s use 16 -bit numbers where 4 -bits are reserved for the fractional part So, Y = $NNN. N Example, What is 375. 875 in Hex? 375 $177 0. 875 = 1*0. 5+1*0. 25+1*0. 125+0*0. 0625 n = %1110 = $E Or, 375. 875 = $177 E 115

Fractional Numbers Example, What is $24 E 3 as a fractional decimal? $24 E 59010 $3 = 0*0. 5+0*0. 25+1*0. 125+1*0. 0625=0. 1875 Or, $24 E 3 = 590. 1875 116