Lab 1 FollowUp Unix Binary Hexadecimal Python Lab

Lab #1 Follow-Up • Unix • Binary / Hexadecimal • Python

Lab #1 Follow-Up • Unix • Binary / Hexadecimal • Python

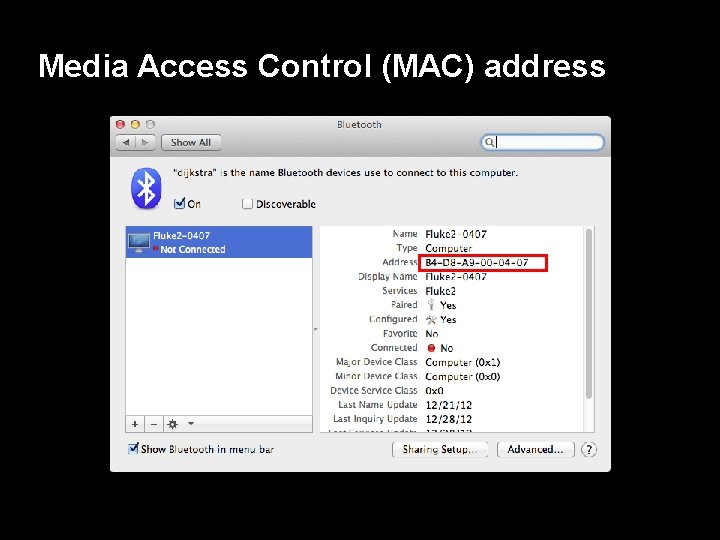
Media Access Control (MAC) address

B 4 -D 8 -A 9 -00 -04 -07
B 4 -D 8 -A 9 -00 -04 -07
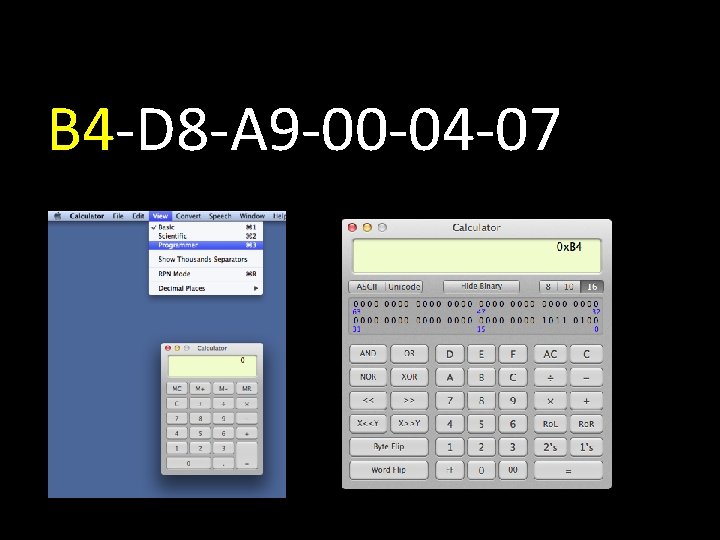
B 4 -D 8 -A 9 -00 -04 -07
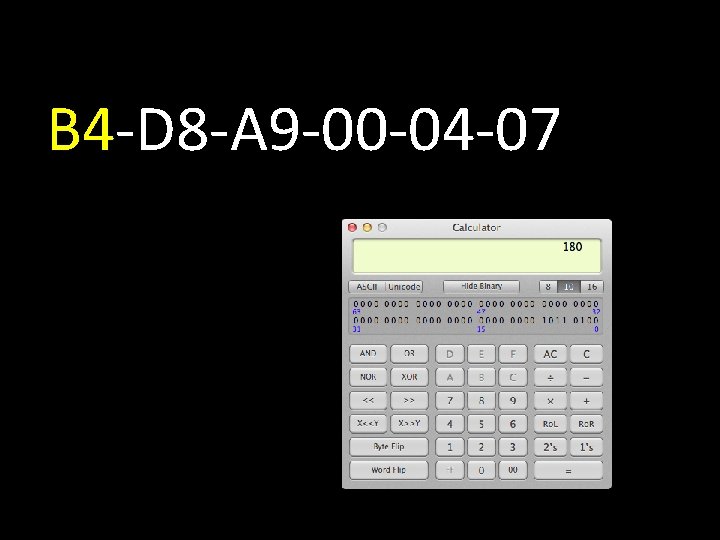
B 4 -D 8 -A 9 -00 -04 -07

Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Hex(adecimal) 0 1 2 3 4 5 6 7 8 9 A B C D E F

Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Hex(adecimal) 0 1 2 3 4 5 6 7 8 9 A B C D E F B 4
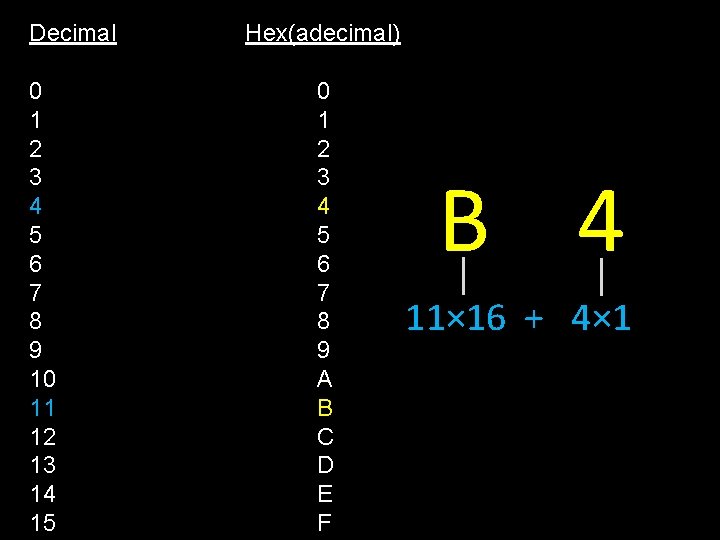
Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Hex(adecimal) 0 1 2 3 4 5 6 7 8 9 A B C D E F B 4 11× 16 + 4× 1
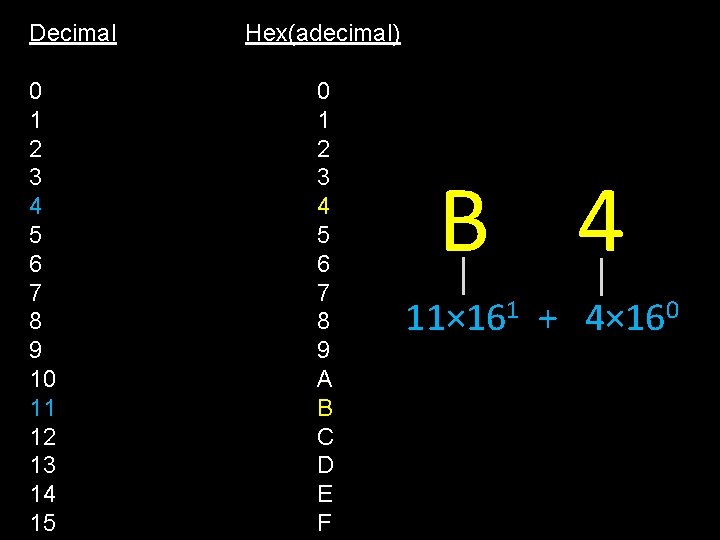
Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Hex(adecimal) 0 1 2 3 4 5 6 7 8 9 A B C D E F B 4 11× 161 + 4× 160
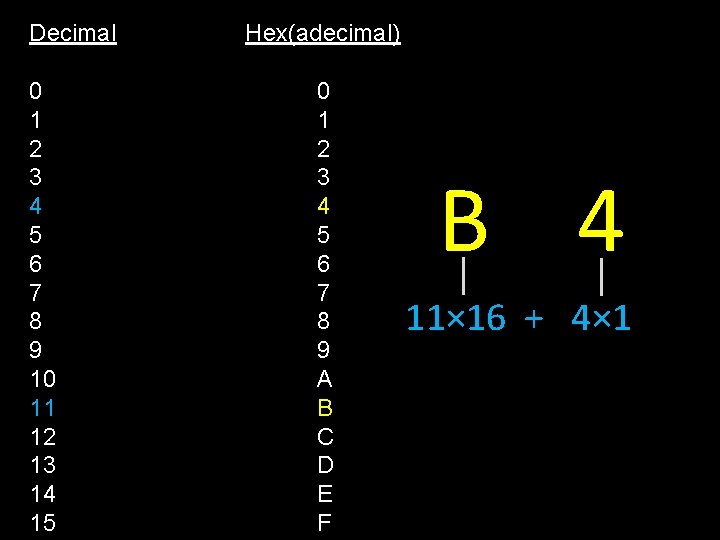
Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Hex(adecimal) 0 1 2 3 4 5 6 7 8 9 A B C D E F B 4 11× 16 + 4× 1

Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Hex(adecimal) 0 1 2 3 4 5 6 7 8 9 A B C D E F B 4 11× 16 + 4× 1 176 + 4

Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Hex(adecimal) 0 1 2 3 4 5 6 7 8 9 A B C D E F B 4 11× 16 + 4× 1 176 + 4 180

All modern numbering systems work this way B 4 11× 161 + 4× 160 11× 16 + 4× 1 176 + 4 180 1 8 0 1× 102 + 8× 101 + 0× 100 1× 100 + 8× 10 + 0× 1 100 + 80 + 180 0

Why Base 16?

Why Base 16? Decimal Hex Binary 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 A B C D E F 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111

Why Base 16? Decimal Hex Binary 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 A B C D E F 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

Eight Bits = One Byte Decimal Hex Binary 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 A B C D E F 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 B 4 1011 0100

Why Base Two?

Why Base Two?

ENIAC (1946)

Faster, Cheaper, Smaller Relay Vacuum tube 1940 s Transistor 1950 s Integrated Circuits 1960 s Today


Binary-to-Decimal Conversion ● ● To convert from binary to decimal • Start from right • Multiply 0, 1 by powers of two (1, 2, 4, 8, …) • Sum of these products is decimal equivalent E. g. , 1 1 0 1 2 = ? ? ? 10

Binary-to-Decimal Conversion ● ● To convert from binary to decimal • Start from right • Multiply 0, 1 by powers of two (1, 2, 4, 8, …) • Sum of these products is decimal equivalent E. g. , 1 1 0 1 2 = ? ? ? 10 1 * 20 = 1

Binary-to-Decimal Conversion ● ● To convert from binary to decimal • Start from right • Multiply 0, 1 by powers of two (1, 2, 4, 8, …) • Sum of these products is decimal equivalent E. g. , 1 1 0 1 2 = ? ? ? 10 + 1 * 20 = 1 0 * 21 = 0

Binary-to-Decimal Conversion ● ● To convert from binary to decimal • Start from right • Multiply 0, 1 by powers of two (1, 2, 4, 8, …) • Sum of these products is decimal equivalent E. g. , 1 1 0 1 2 = ? ? ? 10 + + 1 * 20 = 1 0 * 21 = 0 1 * 22 = 4

Binary-to-Decimal Conversion ● ● To convert from binary to decimal • Start from right • Multiply 0, 1 by powers of two (1, 2, 4, 8, …) • Sum of these products is decimal equivalent E. g. , 1 1 0 1 2 = ? ? ? 10 + + + 1 * 20 = 1 0 * 21 = 0 1 * 22 = 4 1 * 23 = 8

Binary-to-Decimal Conversion ● ● To convert from binary to decimal • Start from right • Multiply 0, 1 by powers of two (1, 2, 4, 8, …) • Sum of these products is decimal equivalent E. g. , 1 1 0 1 2 = 13 10 + + + 1 * 20 = 1 0 * 21 = 0 1 * 22 = 4 1 * 23 = 8 ______ 13

Decimal-to-Binary Conversion To convert from decimal to binary 1. Take remainder of decimal number / 2 2. Write down remainder right-to-left 6 3. If decimal number is zero, we’re done 4. Divide decimal number by 2 3 5. Go to step 1. 13 r 13 ÷ 2= 6 r 2=1 2=0 6 ÷ 3 2= r 2=1 3 ÷ 2= 1 1 r 2=1 1 0 ÷ 2=

Fractions 3. 2510 = ? ? 2

Fractions 3. 2 5 3× 100 + 2× 10 -1 + 5× 10 -2

Fractions 3. 2 5 10 = 1 1. 0 1 2 3× 100 + 2× 10 -1 + 5× 10 -2 1× 21 + 1× 20 + 0× 2 -1 + 1× 2 -2

Problem! 3. 210 = ? ? 2

Google patriot missile failure for a real-world example
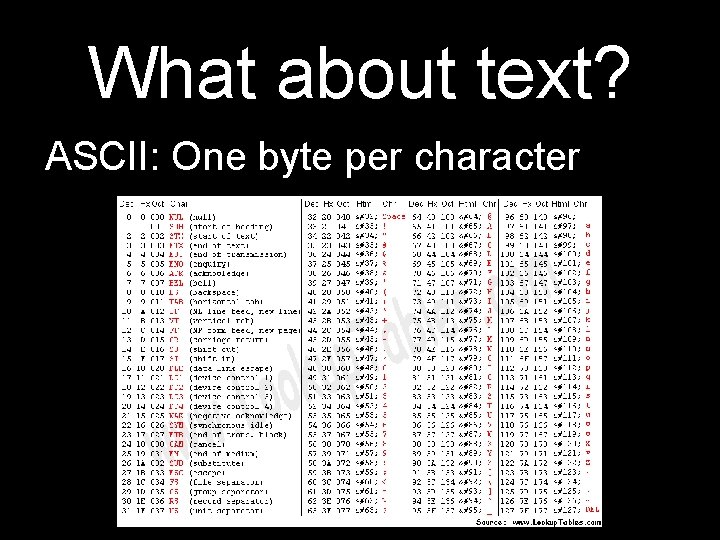
What about text? ASCII: One byte per character

What about text? Unicode: (Up to) two bytes per character

Numbers or text? • Each application (MS Word, Excel) expects either (ASCII) text or (“raw binary”) numbers • Try opening a an Excel spreadsheet in Word. Pad!
- Slides: 40