NUMBERING SYSTEM 1 Analog n Analog information is

NUMBERING SYSTEM 1

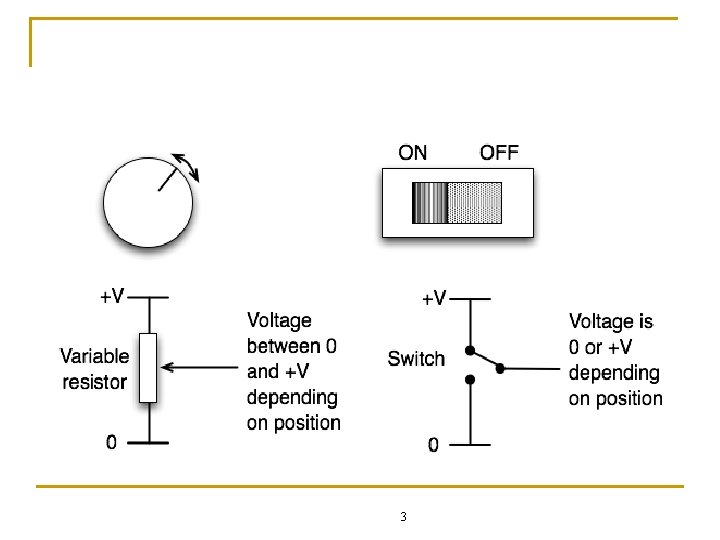
Analog n Analog information is made up of a continuum of values within a given range n At its most basic, digital information can assume only one of two possible values: one/zero, on/off, high/low, true/false, etc. 2

3

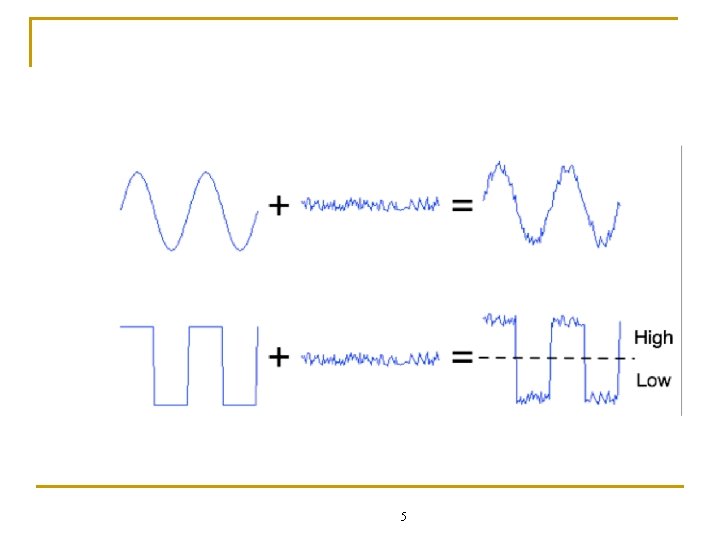
Digital n n Digital Information is less susceptible to noise than analog information Exact voltage values are not important, only their class (1 or 0) The complexity of operations is reduced, thus it is easier to implement them with high accuracy in digital form BUT: Most physical quantities are analog, thus a conversion is needed 4

5

Digital Number Systems n Many number systems are used in digital electronics: q q Decimal number system (base 10) Binary number system (base 2) Octal number system (base 8) Hexadecimal number system (base 16) 6

Decimal system n n We use decimal numbers everyday. It is a base-10 system. 10 symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 The position of each digit in a decimal number can be assigned a weight. 7

Decimal system n n n Most significant digit (MSD) - the digit that carries the most weight, usually the left most Least significant digit (LSD) - the digit that carries the least weight, usually the right most Take example: decimal number 2745. 214 Weights 103 102 101 100 2 7 4 5 . 8 10 -1 10 -2 10 -3 2 1 4

Binary system n n Difficult to design a system that works with 10 different voltage levels Solution is base-2 (binary) system 2 digits/symbols: 0, 1 Examples: 0, 1, 01, 111, 101010 9

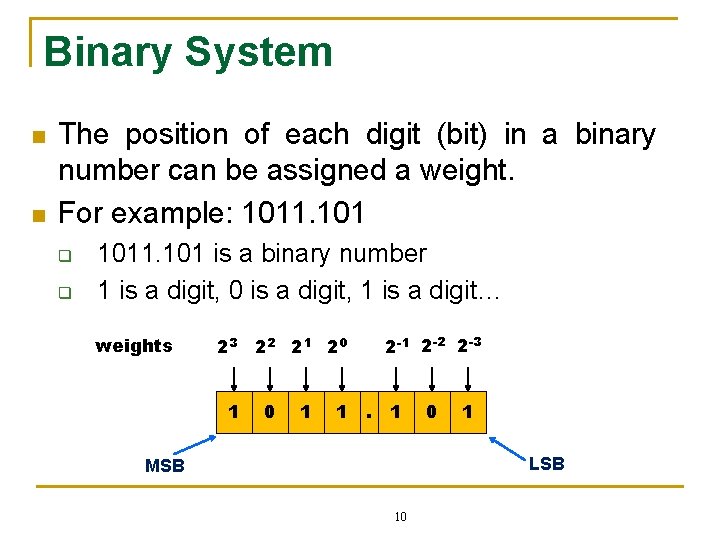
Binary System n n The position of each digit (bit) in a binary number can be assigned a weight. For example: 1011. 101 q q 1011. 101 is a binary number 1 is a digit, 0 is a digit, 1 is a digit… weights 2 -1 2 -2 2 -3 23 22 21 20 1 1 . 1 0 1 LSB MSB 10

Binary System (BIT) n n It takes more digits in the binary system to represent the same value in the decimal system. Examples: 710 = 1112 1010 102 A single binary digit is referred to as a bit. 8 bits make a byte. 11

Binary System (BIT) n n n With N bits we have 2 N discrete values. For example, a 4 -bit system can represent 24 or 16 discrete values. The largest value is always 2 N – 1. For the 4 -bit system, 24 – 1 = 1510. The range of values for a 4 -bit number is then 0 thru 15. 12

Hexadecimal System n n Base-16 system 16 symbols: 10 numeric digits and 6 alphabetic characters 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Compact way of writing binary system. Widely used in computer and microprocessor applications. 13

Hexadecimal System n n n Examples: 1 C 16 , A 8516 The position of each digit in a hexadecimal number can be assigned a weight For example: 2 AF 8. 98 E Weights 163 162 161 160 2 A F 8 14 16 -1 16 -2 16 -3. 9 8 E

Octal System n n n Base-8 system. 8 digits: 0, 1, 2, 3, 4, 5, 6, 7 Convenient way to express binary numbers and codes. 15

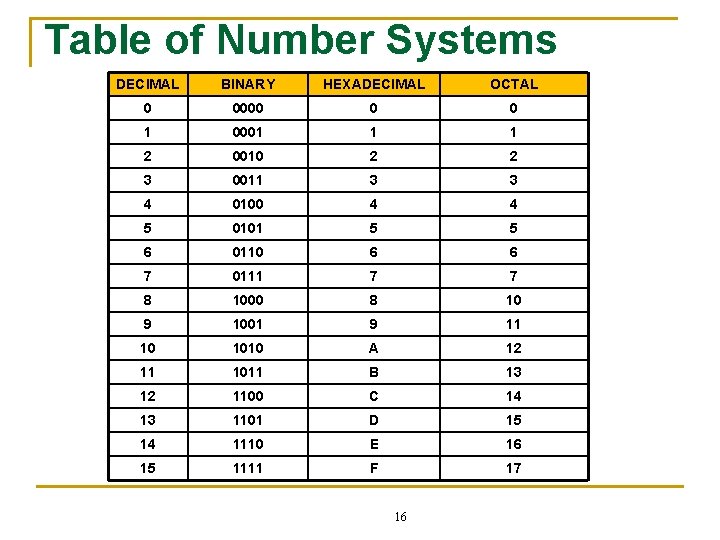
Table of Number Systems DECIMAL BINARY HEXADECIMAL OCTAL 0 0000 0 0 1 0001 1 1 2 0010 2 2 3 0011 3 3 4 0100 4 4 5 0101 5 5 6 0110 6 6 7 0111 7 7 8 1000 8 10 9 1001 9 11 10 1010 A 12 11 1011 B 13 12 1100 C 14 13 1101 D 15 14 1110 E 16 15 1111 F 17 16

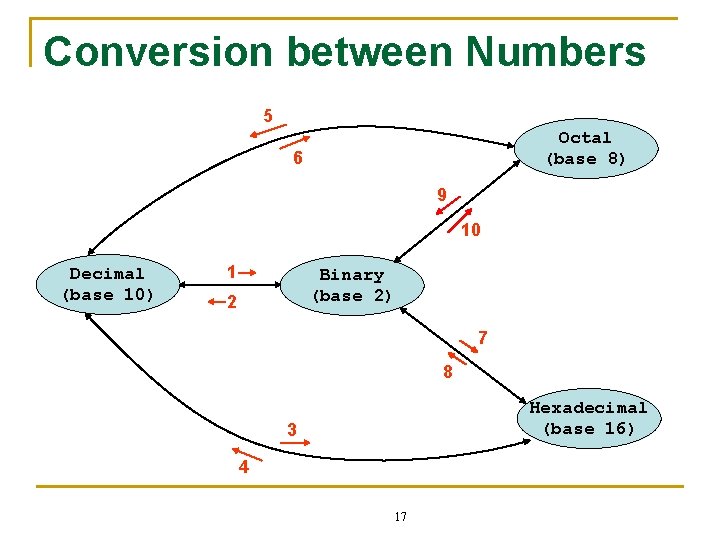
Conversion between Numbers 5 Octal (base 8) 6 9 10 Decimal (base 10) 1 Binary (base 2) 2 7 8 Hexadecimal (base 16) 3 4 17

1. Decimal to Binary n Method 1: Decimal number binary number q n Method 2: Decimal whole number binary number. q n Method: sum-of-weights Method: division-by-2 Method 3: Decimal fraction binary number q Method: multiplication-by-2 18

Method 1: Sum of Weights n Step 1: Find the power of two that fulfills the following: q q n n n Nearest to the given decimal number; and Its decimal number is less than or equal to the given decimal number. Step 2: Subtract the power of two (from Step 1) from the given decimal number. Step 3: If the result of the subtraction in Step 2 is 0, go to Step 4. Else, repeat Steps 1 and 2 for the result of the subtraction in Step 2. Step 4: Write out the binary number based on all the powers of two from Step 1. 19

Method 1: Sum of Weights Example 1: Convert 2510 to binary Step 1: 22 = 4? No, because it is not the nearest. 23 = 8 is nearer and still less than 25. 24 = 16 is the nearest and its decimal, 16 is less than 25. 25 = 32 No, because its decimal number, 32 is more than 25. Step 2: the result of subtraction 25 – 16 = 9 Step 3: Repeat Step 1: the power of two which is nearest to 9 but less than 9 is 23 = 8 Repeat Step 2: the result of subtraction 9 – 8 = 1 Repeat Step 1: the power of two which is nearest to 1 and equal to 1 is 2 0 = 1 Repeat Step 2: the result of subtraction 1 – 1 = 0 Step 4: Write out the binary number based on all the powers of two from Step 1. Weights Binary number 24 23 22 21 20 1 1 0 20 0 1

Method 2: Division-by-2 n n n Method 2 is used to convert only whole decimal numbers (no fraction) to binary. Repeat the division of the decimal number with 2 until the quotient is 0. Remainder of each division determine the binary number. First remainder represent the LSB and the last remainder is the MSB. 21

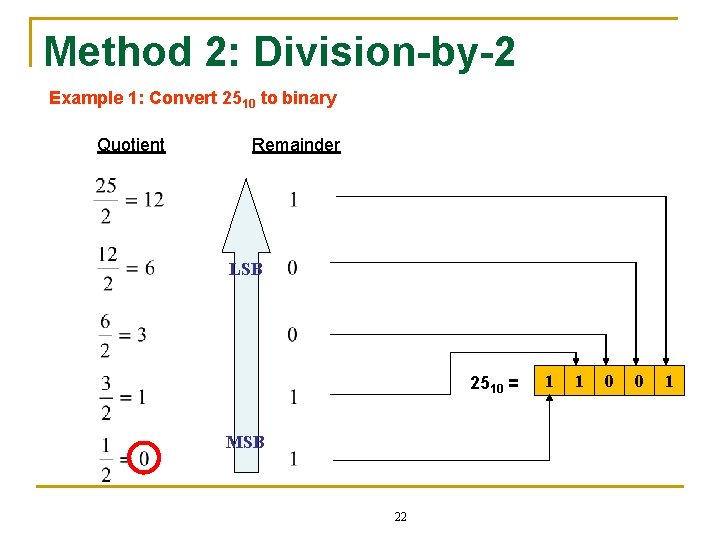
Method 2: Division-by-2 Example 1: Convert 2510 to binary Quotient Remainder LSB 2510 = MSB 22 1 1 0 0 1

Method 3: Multiplication-by-2 n n n Method 3 is used to convert decimal fraction only to binary. Repeat the multiplication until the fractional part of the product are all zeros. The binary number is determined by the first digit in the multiplication results. 23

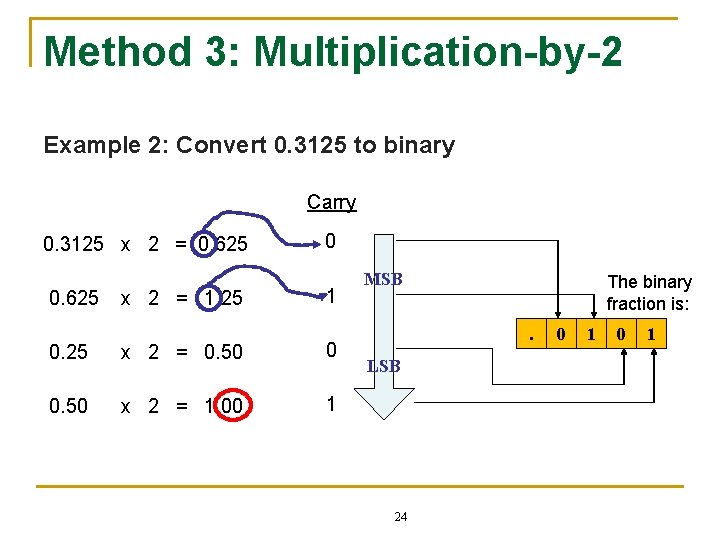
Method 3: Multiplication-by-2 Example 2: Convert 0. 3125 to binary Carry 0. 3125 x 2 = 0. 625 x 2 = 1. 25 0 1 0. 25 x 2 = 0. 50 0 0. 50 x 2 = 1. 00 1 MSB The binary fraction is: . LSB 24 0 1

2. Binary to Decimal n Only one method is used. That is the sum of weight. Example 3: Convert 1011. 101 to decimal 2 -1 2 -2 2 -3 23 22 21 20 1 1 . 1 0 1 =(1 x 23) + (0 x 22) + (1 x 21) + (1 x 20) + (1 x 2 -1) + (0 x 2 -2) + (1 x 2 -3) = 8 + 0 + 2 + 1 + 0. 5 + 0. 125 = 11. 62510 25

3. Decimal to Hexadecimal n n n Method used is repeated division by-16. Repeat the division of the decimal number with 16 until the quotient is 0. Remainder of each division determine the hex number. First remainder represent the LSB and the last remainder is the MSB. 26

Decimal to Hexadecimal Example 4: Convert 65010 to hex number Quotient Remainder (decimal) Remainder (hexadecimal) LSB MSB 65010 = 2 27 8 A

4. Hexadecimal to Decimal n Only one method is used. That is the sum of weight. Example 5: Convert A 8516 to decimal number 162 161 160 A 8 5 = (A x 162) + (8 x 161) + (5 x 160) = (10 x 256) + (8 x 16) + (5 x 1) = 2560 + 128 + 5 = 2693 28

5. Decimal to Octal n n n Method used is repeated division by-8. Repeat the division of the decimal number with 8 until the quotient is 0. Remainder of each division determine the oct number. First remainder represent the LSB and the last remainder is the MSB. 29

Decimal to Octal Example 6: Convert 35910 to octal number Quotient Remainder LSB MSB 35910 = 5 30 4 7

6. Octal to Decimal n Only one method is used. That is the sum of weight. Example 7: Convert 23748 to decimal number 83 82 81 80 2 3 7 4 = (2 x 83) + (3 x 82) + (7 x 81) + (4 x 80) = (2 x 512) + (3 x 64) + (7 x 8) + (4 x 1) = 1024 + 192 + 56 + 4 = 1276 31

7. Binary to Hexadecimal n n Step 1: Break the binary number into 4 -bit groups, starting from LSB. Step 2: Replace each 4 -bit with the equivalent hexadecimal number. Example 8: Convert 111111000101101001 to hex number Binary Hexadecimal 0011 1111 0001 0110 1001 3 F 1 32 6 9

8. Hexadecimal to Binary n Step: Replace each digit of the hexadecimal number with the equivalent 4 -bit binary number. Example 9: Convert CF 8 E 16 to binary number Hexadecimal Binary C F 8 E 1100 1111 1000 1110 33

9. Binary to Octal n n Step 1: Break the binary number into 3 -bit groups, starting from LSD. Step 2: Replace each 3 -bit group with the equivalent octal number. Example 10: Convert 1011110012 to octal number Binary 101 111 001 Octal 5 7 1 34

10. Octal to Binary n Step: Replace each digit of the octal number with the equivalent 3 -bit binary number. Example 11: Convert 75268 to binary number Octal Binary 7 5 2 6 111 101 010 110 35

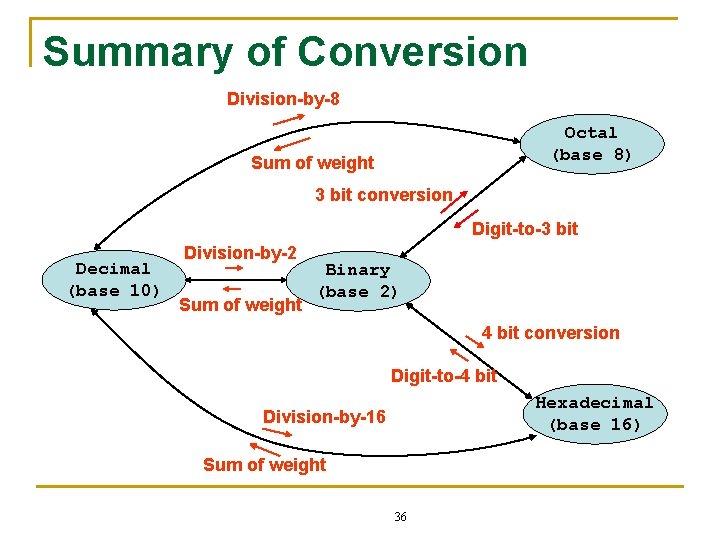
Summary of Conversion Division-by-8 Octal (base 8) Sum of weight 3 bit conversion Digit-to-3 bit Decimal (base 10) Division-by-2 Sum of weight Binary (base 2) 4 bit conversion Digit-to-4 bit Hexadecimal (base 16) Division-by-16 Sum of weight 36