Review on Number Systems Decimal Binary and Hexadecimal

Review on Number Systems Decimal, Binary, and Hexadecimal 1

Base-N Number System q Base N q N Digits: 0, 1, 2, 3, 4, 5, …, N-1 q Example: 1045 N q Positional Number System q • Digit do is the least significant digit (LSD). • Digit dn-1 is the most significant digit (MSD). 2

Decimal Number System q Base 10 q Ten Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 q Example: 104510 q Positional Number System q Digit d 0 is the least significant digit (LSD). q Digit dn-1 is the most significant digit (MSD). 3

Binary Number System q Base 2 q Two Digits: 0, 1 q Example: 10101102 q Positional Number System q Binary Digits are called Bits q Bit bo is the least significant bit (LSB). q Bit bn-1 is the most significant bit (MSB). 4

Definitions q nybble = 4 bits q byte = 8 bits q (short) word = 2 bytes = 16 bits q (double) word = 4 bytes = 32 bits q (long) word = 8 bytes = 64 bits q 1 K (kilo or “kibi”) = 1, 024 q 1 M (mega or “mebi”) = (1 K)*(1 K) = 1, 048, 576 q 1 G (giga or “gibi”) = (1 K)*(1 M) = 1, 073, 741, 824 5
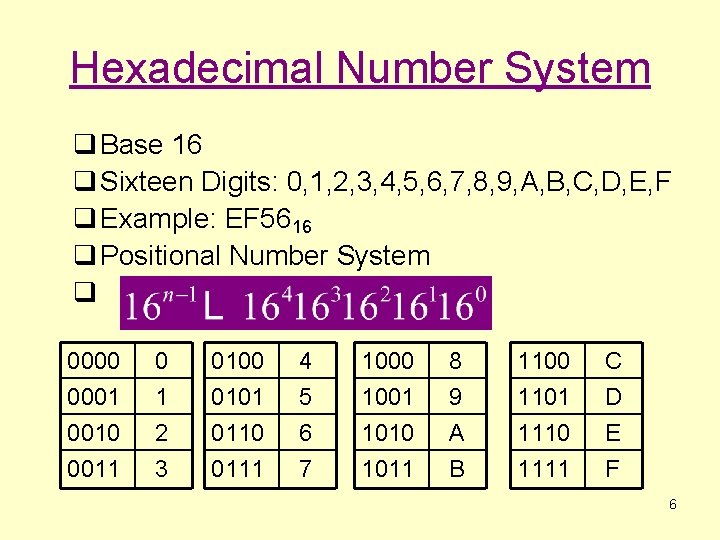
Hexadecimal Number System q Base 16 q Sixteen Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F q Example: EF 5616 q Positional Number System q 0000 0001 0010 0011 0 1 2 3 0100 0101 0110 0111 4 5 6 7 1000 1001 1010 1011 8 9 A B 1100 1101 1110 1111 C D E F 6

Binary Addition • Single Bit Addition Table 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 Note “carry” 7

Hex Addition • 4 -bit Addition 4 + 4 = 8 4 + 8 = C 8 + 7 = F F + E = 1 D Note “carry” 8

Hex Digit Addition Table + 0 1 0 0 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 8 8 8 9 9 9 A A A B B B C C C D D D E E E F F F 10 2 2 3 4 5 6 7 8 9 A B C D E F 10 11 3 3 4 5 6 7 8 9 A B C D E F 10 11 12 4 4 5 6 7 8 9 A B C D E F 10 11 12 13 5 5 6 7 8 9 A B C D E F 10 11 12 13 14 6 6 7 8 9 A B C D E F 10 11 12 13 14 15 7 7 8 9 A B C D E F 10 11 12 13 14 15 16 8 8 9 A B C D E F 10 11 12 13 14 15 16 17 9 9 A B C D E F 10 11 12 13 14 15 16 17 18 A A B C D E F 10 11 12 13 14 15 16 17 18 19 B B C D E F 10 11 12 13 14 15 16 17 18 19 1 A C C D E F 10 11 12 13 14 15 16 17 18 19 1 A 1 B D D E F 10 11 12 13 14 15 16 17 18 19 1 A 1 B 1 C E E F 10 11 12 13 14 15 16 17 18 19 1 A 1 B 1 C 1 D F F 10 11 12 13 14 15 16 17 18 19 1 A 1 B 1 C 1 D 1 E 9

1’s Complements q 1’s complement (or Ones’ Complement) § To calculate the 1’s complement of a binary number just “flip” each bit of the original binary number. § E. g. 0 1 , 1 0 § 01010100100 10101011011 10

Why choose 2’s complement? 11

2’s Complements q 2’s complement § To calculate the 2’s complement just calculate the 1’s complement, then add 1. 01010100100 10101011011 + 1= 10101011100 § Handy Trick: Leave all of the least significant 0’s and first 1 unchanged, and then “flip” the bits for all other digits. q. Eg: 01010100100 -> 10101011100 12

Complements q. Note the 2’s complement of the 2’s complement is just the original number N § EX: let N = 01010100100 § (2’s comp of N) = M = 10101011100 § (2’s comp of M) = 01010100100 = N 13

Two’s Complement Representation for Signed Numbers q. Let’s introduce a notation for negative digits: § For any digit d, define d = −d. q. Notice that in binary, where d {0, 1}, we have: q. Two’s complement notation: § To encode a negative number, we implicitly negate the leftmost (most significant) bit: v. E. g. , 1000 = (− 1)000 = − 1· 23 + 0· 22 + 0· 21 + 0· 20 = − 8 14

Negating in Two’s Complement q. Theorem: To negate a two’s complement number, just complement it and add 1. q. Proof (for the case of 3 -bit numbers XYZ): 15

Signed Binary Numbers q. Two methods: § First method: sign-magnitude v. Use one bit to represent the sign • 0 = positive, 1 = negative v. Remaining bits are used to represent the magnitude v. Range - (2 n-1 – 1) to 2 n-1 - 1 where n=number of digits v. Example: Let n=4: Range is – 7 to 7 or v 1111 to 0111 16

Signed Binary Numbers q. Second method: Two’s-complement v. Use the 2’s complement of N to represent -N v. Note: MSB is 0 if positive and 1 if negative v. Range - 2 n-1 to 2 n-1 -1 where n=number of digits v. Example: Let n=4: Range is – 8 to 7 Or 1000 to 0111 17
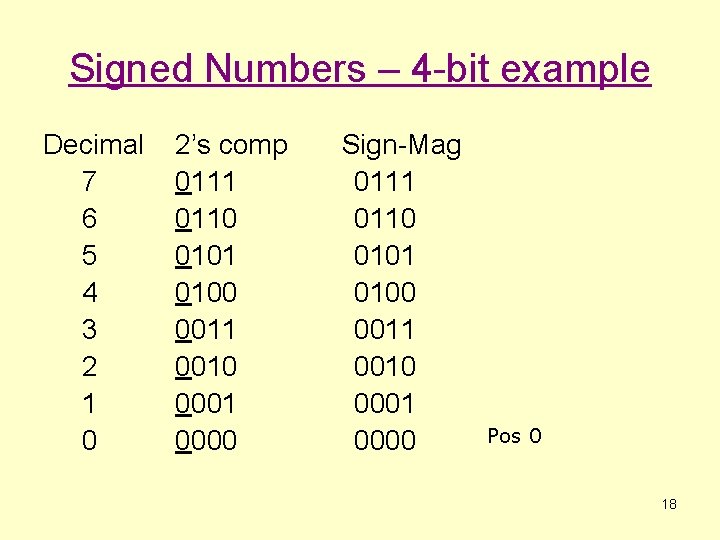
Signed Numbers – 4 -bit example Decimal 7 6 5 4 3 2 1 0 2’s comp 0111 0110 0101 0100 0011 0010 0001 0000 Sign-Mag 0111 0110 0101 0100 0011 0010 0001 0000 Pos 0 18

Signed Numbers-4 bit example Decimal -8 -7 -6 -5 -4 -3 -2 -1 -0 2’s comp Sign-Mag 1000 N/A 1001 1111 1010 1110 1011 1100 1101 1011 1110 1010 1111 1001 0000 (= +0) 1000 19

Signed Numbers-8 bit example 20

Notes: q “Humans” normally use sign-magnitude representation for signed numbers § Eg: Positive numbers: +N or N § Negative numbers: -N q Computers generally use two’s-complement representation for signed numbers § First bit still indicates positive or negative. § If the number is negative, take 2’s complement to determine its magnitude v. Or, just add up the values of bits at their positions, remembering that the first bit is implicitly negative. 21

Examples q Let N=4: two’s-complement q What is the decimal equivalent of 01012 Since MSB is 0, number is positive 01012 = 4+1 = +510 q What is the decimal equivalent of 11012 = v. Since MSB is one, number is negative v. Must calculate its 2’s complement v 11012 = −(0010+1)= − 00112 or − 310 22

Very Important!!! – Unless otherwise stated, assume two’scomplement numbers for all problems, quizzes, HW’s, etc. The first digit will not necessarily be explicitly underlined. 23

Arithmetic Subtraction q. Borrow Method § This is the technique you learned in grade school § For binary numbers, we have § 0 - 0 = 0 1 - 0 = 1 1 - 1 = 0 1 0 - 1 = 1 with a “borrow” 24

Binary Subtraction q. Note: § A – (+B) = A + (-B) § A – (-B) = A + (-(-B))= A + (+B) § In other words, we can “subtract” B from A by “adding” –B to A. § However, -B is just the 2’s complement of B, so to perform subtraction, we v 1. Calculate the 2’s complement of B v 2. Add A + (-B) 25

Binary Subtraction - Example q. Let n=4, A=01002 (410), and B=00102 (210) q. Let’s find A+B, A-B and B-A A+B 0 1 0 0 (4)10 + 0 0 1 0 (2)10 0 11 0 6 26

Binary Subtraction - Example A-B A+ (-B) 0 1 0 0 (4)10 - 0 0 1 0 (2)10 0 1 0 0 (4)10 + 1 1 1 0 (-2)10 10 0 1 0 2 “Throw this bit” away since n=4 27

Binary Subtraction - Example B-A B + (-A) 0 0 1 0 (2)10 - 0 1 0 0 (4)10 0 0 1 0 (2)10 + 1 1 0 0 (-4)10 1110 -2 1 1 1 02 = - 0 0 1 02 = -210 28

“ 16’s Complement” method q. The 16’s complement of a 16 bit Hexadecimal number is just: =1000016 – N 16 q. Q: What is the decimal equivalent of B 2 CE 16 ? 29

16’s Complement q. Since sign bit is one, number is negative. Must calculate the 16’s complement to find magnitude. 1000016 – B 2 CE 16 = ? q. We have 10000 - B 2 CE 30

16’s Complement FFF 10 - B 2 CE 4 D 3 2 31

16’s Complement q. So, 1000016 – B 2 CE 16 = 4 D 3216 = 4× 4, 096 + 13× 256 + 3× 16 + 2 = 19, 76210 q. Thus, B 2 CE 16 (in signed-magnitude) represents -19, 76210. 32

Why does 2’s complement work? 33

Sign Extension 34

Sign Extension q Assume a signed binary system q Let A = 0101 (4 bits) and B = 010 (3 bits) q What is A+B? § To add these two values we need A and B to be of the same bit width. § Do we truncate A to 3 bits or add an additional bit to B? 35

Sign Extension q A = 0101 and B=010 q Can’t truncate A! Why? § § A: 0101 -> 101 But 0101 <> 101 in a signed system 0101 = +5 101 = -3 36

Sign Extension q Must “sign extend” B, q so B becomes 010 -> 0010 q Note: Value of B remains the same So 0101 (5) +0010 (2) Sign bit is extended -------0111 (7) 37

Sign Extension q What about negative numbers? q Let A=0101 and B=100 q Now B = 100 1100 0101 +1100 ------10001 Throw away Sign bit is extended (5) (-4) (1) 38

Why does sign extension work? q Note that: (− 1) = 1111 = 111… 1 § Thus, any number of leading 1’s is equivalent, so long as the leftmost one of them is implicitly negative. q Proof: 111… 1 = −(111… 1) = = −(100… 0 − 11… 1) = −(1) q So, the combined value of any sequence of leading ones is always just − 1 times the position value of the rightmost 1 in the sequence. 111… 100… 0 = (− 1)· 2 n n 39

Number Conversions 40

Decimal to Binary Conversion Method I: Use repeated subtraction. Subtract largest power of 2, then next largest, etc. Powers of 2: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2 n Exponent: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 , n 20 21 22 23 24 25 26 27 28 29 210 2 n 41

Decimal to Binary Conversion Suppose x = 156410 Subtract 1024: Subtract 512: 1564 -1024 (210) = 540 n=10 or 1 in the (210)’s position 540 -512 (29) = 28 n=9 or 1 in the (29)’s position 28=256, 27=128, 26=64, 25=32 > 28, so we have 0 in all of these positions Subtract 16: 28 -16 (24) = 12 n=4 or 1 in (24)’s position Subtract 8: Subtract 4: 12 – 8 (23) = 4 4 – 4 (22) = 0 n=3 or 1 in (23)’s position n=2 or 1 in (22)’s position Thus: 156410 = (1 1 0 0 1 1 1 0 0)2 42

Decimal to Binary Conversion Method II: Use repeated division by radix. 2 | 1564 2|__24_ 782 R=0 2|_____ 12 R=0 2|_____ 391 R=0 2|_____ 6 R=0 2|_____ 3 R= 0 195 R=1 2|_____ 1 R=1 97 R=1 2|_____ 48 R=1 0 R=1 24 R = 0 Collect remainders in reverse order 11000011100 43

Binary to Hex Conversion 1. Divide binary number into 4 -bit groups 01 1 0 0 1 1 1 0 0 Pad with 0’s If unsigned number 2. Substitute hex digit for each group Pad with sign bit if signed number 61 C 16 44

Hexadecimal to Binary Conversion Example 1. Convert each hex digit to equivalent binary (1 E 9 C)16 (0001 1110 1001 1100)2 45

Decimal to Hex Conversion Method II: Use repeated division by radix. 16 | 1564 97 16|_____ 6 16|_____ 0 R = 12 = C R=1 R=6 N = 61 C 16 46
- Slides: 46