Number Systems Decimal Binary and Hexadecimal 1 BaseN

Number Systems Decimal, Binary, and Hexadecimal 1

Base-N Number System • • • Base N N Digits: 0, 1, 2, 3, 4, 5, …, N-1 Example: 1045 N Positional Number System • Digit do is the least significant digit (LSD). • Digit dn-1 is the most significant digit (MSD). 2

Decimal Number System • • Base 10 Ten Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Example: 104510 Positional Number System • Digit d 0 is the least significant digit (LSD). • Digit dn-1 is the most significant digit (MSD). 3

Binary Number System • • Base 2 Two Digits: 0, 1 Example: 10101102 Positional Number System • Binary Digits are called Bits • Bit bo is the least significant bit (LSB). • Bit bn-1 is the most significant bit (MSB). 4

Definitions • • nybble = 4 bits byte = 8 bits (short) word = 2 bytes = 16 bits (double) word = 4 bytes = 32 bits (long) word = 8 bytes = 64 bits 1 K (kilo or “kibi”) = 1, 024 1 M (mega or “mebi”) = (1 K)*(1 K) = 1, 048, 576 1 G (giga or “gibi”) = (1 K)*(1 M) = 1, 073, 741, 824 5

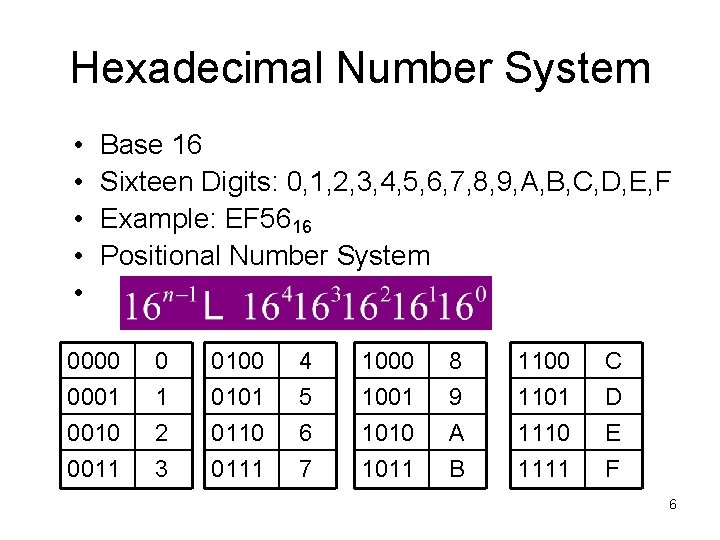
Hexadecimal Number System • • • Base 16 Sixteen Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Example: EF 5616 Positional Number System 0000 0001 0010 0011 0 1 2 3 0100 0101 0110 0111 4 5 6 7 1000 1001 1010 1011 8 9 A B 1100 1101 1110 1111 C D E F 6

Collaborative Learning methodology in which students are not only responsible for their own learning but for the learning of other members of the group. 7

Think - Pair - Share (TPS) Quizzes • Think – Pair – Share – Think individually for one time units – Pair with partner for two time units – Share with group for one and half time units – Report results 8

Quiz 1 -A (Practice) • Assemble in groups of 4 • Question: Convert the following binary number into its decimal equivalent: 110102 9

Quiz 1 -A (Practice) THINK One Unit (e. g. 30 Seconds) 10

Quiz 1 -A (Practice) PAIR Two Units (e. g. 60 Seconds) 11

Quiz 1 -A (Practice) SHARE 1. 5 units (e. g. 45 Seconds) 12

Quiz 1 -A (Practice) Report • Write names of all group members and the consensus answer on one sheet of paper. • All sheets will be collected. • One will be picked at random to read to the class. • All papers will be graded! 13

Quiz 1 -A Solution • Convert the following number into base 10 decimal: 14

Quiz 1 -B • Convert the following number into base 10 decimal: 1010116 15

Collaborative Learning • • Think for 30 seconds Pair for 1 minute Share for 45 seconds Report 16

Quiz 1 -B Solution • Convert the following number into base 10 decimal: 1010116 = 1· 164 + 0· 163 + 1· 162 + 0· 161 + 1· 160 = 164 + 162 + 160 = 65, 536 + 256 + 1 = 65, 793 17

TPS Quiz 2 18

Binary Addition • Single Bit Addition Table 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 Note “carry” 19

Hex Addition • 4 -bit Addition 4 + 4 = 8 4 + 8 = C 8 + 7 = F F + E = 1 D Note “carry” 20

Hex Digit Addition Table + 0 1 0 0 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 7 7 8 8 8 9 9 9 A A A B B B C C C D D D E E E F F F 10 2 2 3 4 5 6 7 8 9 A B C D E F 10 11 3 3 4 5 6 7 8 9 A B C D E F 10 11 12 4 4 5 6 7 8 9 A B C D E F 10 11 12 13 5 5 6 7 8 9 A B C D E F 10 11 12 13 14 6 6 7 8 9 A B C D E F 10 11 12 13 14 15 7 7 8 9 A B C D E F 10 11 12 13 14 15 16 8 8 9 A B C D E F 10 11 12 13 14 15 16 17 9 9 A B C D E F 10 11 12 13 14 15 16 17 18 A A B C D E F 10 11 12 13 14 15 16 17 18 19 B B C D E F 10 11 12 13 14 15 16 17 18 19 1 A C C D E F 10 11 12 13 14 15 16 17 18 19 1 A 1 B D D E F 10 11 12 13 14 15 16 17 18 19 1 A 1 B 1 C E E F 10 11 12 13 14 15 16 17 18 19 1 A 1 B 1 C 1 D F F 10 11 12 13 14 15 16 17 18 19 1 A 1 B 1 C 1 D 1 E 21

TPS Quiz 3 22

Complements • 1’s complement – To calculate the 1’s complement of a binary number just “flip” each bit of the original binary number. – E. g. 0 1 , 1 0 – 01010100100 10101011011 23

Complements • 2’s complement – To calculate the 2’s complement just calculate the 1’s complement, then add 1. 01010100100 10101011011 + 1= 10101011100 – Handy Trick: Leave all of the least significant 0’s and first 1 unchanged, and then “flip” the bits for all other digits. • Eg: 01010100100 -> 10101011100 24

Complements • Note the 2’s complement of the 2’s complement is just the original number N – EX: let N = 01010100100 – 2’s comp of N = M = 10101011100 – 2’s comp of M = 01010100100 = N 25

Two’s Complement Representation for Signed Numbers • Let’s introduce a notation for negative digits: – For any digit d, define d = −d. • Notice that in binary, where d {0, 1}, we have: • Two’s complement notation: – To encode a negative number, we implicitly negate the leftmost (most significant) bit: • E. g. , 1000 = (− 1)000 = − 1· 23 + 0· 22 + 0· 21 + 0· 20 = − 8 26

Negating in Two’s Complement • Theorem: To negate a two’s complement number, just complement it and add 1. • Proof (for the case of 3 -bit numbers XYZ): 27

Signed Binary Numbers • Two methods: – First method: sign-magnitude • Use one bit to represent the sign – 0 = positive, 1 = negative • Remaining bits are used to represent the magnitude • Range - (2 n-1 – 1) to 2 n-1 - 1 where n=number of digits • Example: Let n=4: Range is – 7 to 7 or • 1111 to 0111 28

Signed Binary Numbers • Second method: Two’s-complement • Use the 2’s complement of N to represent -N • Note: MSB is 0 if positive and 1 if negative • Range - 2 n-1 to 2 n-1 -1 where n=number of digits • Example: Let n=4: Range is – 8 to 7 Or 1000 to 0111 29

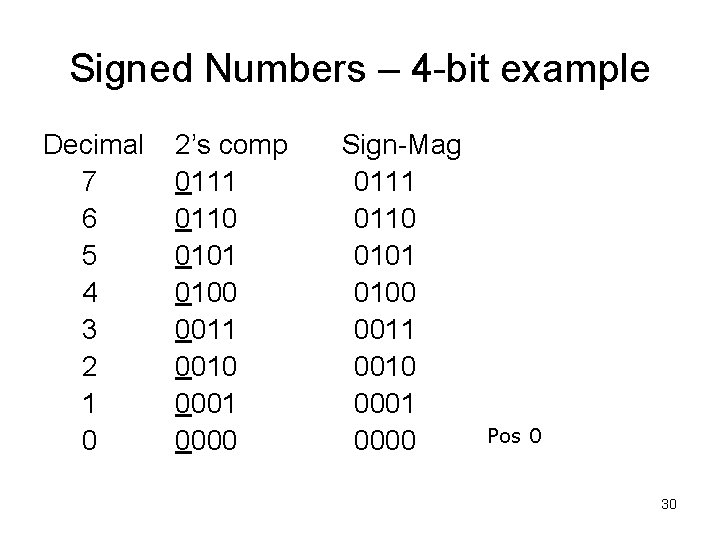
Signed Numbers – 4 -bit example Decimal 7 6 5 4 3 2 1 0 2’s comp 0111 0110 0101 0100 0011 0010 0001 0000 Sign-Mag 0111 0110 0101 0100 0011 0010 0001 0000 Pos 0 30

Signed Numbers-4 bit example Decimal -8 -7 -6 -5 -4 -3 -2 -1 -0 2’s comp Sign-Mag 1000 N/A 1001 1111 1010 1110 1011 1100 1101 1011 1110 1010 1111 1001 0000 (= +0) 1000 31

Notes: • “Humans” normally use sign-magnitude representation for signed numbers – Eg: Positive numbers: +N or N – Negative numbers: -N • Computers generally use two’s-complement representation for signed numbers – First bit still indicates positive or negative. – If the number is negative, take 2’s complement to determine its magnitude • Or, just add up the values of bits at their positions, remembering that the first bit is implicitly negative. 32

Example • Let N=4: two’s-complement • What is the decimal equivalent of 01012 Since msb is 0, number is positive 01012 = 4+1 = +510 • What is the decimal equivalent of 11012 = • Since MSB is one, number is negative • Must calculate its 2’s complement • 11012 = −(0010+1)= − 00112 or − 310 33

Very Important!!! – Unless otherwise stated, assume two’scomplement numbers for all problems, quizzes, HW’s, etc. The first digit will not necessarily be explicitly underlined. 34

TPS Quizzes 5 -7 35

Arithmetic Subtraction • Borrow Method – This is the technique you learned in grade school – For binary numbers, we have – 0 - 0 = 0 1 - 0 = 1 1 - 1 = 0 1 0 - 1 = 1 with a “borrow” 36

Binary Subtraction • Note: – A – (+B) = A + (-B) – A – (-B) = A + (-(-B))= A + (+B) – In other words, we can “subtract” B from A by “adding” –B to A. – However, -B is just the 2’s complement of B, so to perform subtraction, we • 1. Calculate the 2’s complement of B • 2. Add A + (-B) 37

Binary Subtraction - Example • Let n=4, A=01002 (410), and B=00102 (210) • Let’s find A+B, A-B and B-A A+B 0 1 0 0 (4)10 + 0 0 1 0 (2)10 0 11 0 6 38

Binary Subtraction - Example A-B A+ (-B) 0 1 0 0 (4)10 - 0 0 1 0 (2)10 0 1 0 0 (4)10 + 1 1 1 0 (-2)10 10 0 1 0 2 “Throw this bit” away since n=4 39

Binary Subtraction - Example B-A B + (-A) 0 0 1 0 (2)10 - 0 1 0 0 (4)10 0 0 1 0 (2)10 + 1 1 0 0 (-4)10 1110 -2 1 1 1 02 = - 0 0 1 02 = -210 40

“ 16’s Complement” method • The 16’s complement of a 16 bit Hexadecimal number is just: • =1000016 – N 16 • Q: What is the decimal equivalent of B 2 CE 16 ? 41

16’s Complement • Since sign bit is one, number is negative. Must calculate the 16’s complement to find magnitude. • =1000016 – B 2 CE 16 = ? ? ? • We have 10000 - B 2 CE 42

16’s Complement FFF 10 - B 2 CE 4 D 3 2 43

16’s Complement • So, 1000016 – B 2 CE 16 = 4 D 3216 = 4× 4, 096 + 13× 256 + 3× 16 + 2 = 19, 76210 • Thus, B 2 CE 16 (in signed-magnitude) represents -19, 76210. 44

Sign Extension 45

Sign Extension • • • Assume a signed binary system Let A = 0101 (4 bits) and B = 010 (3 bits) What is A+B? – To add these two values we need A and B to be of the same bit width. – Do we truncate A to 3 bits or add an additional bit to B? 46

Sign Extension • • A = 0101 and B=010 Can’t truncate A!! Why? – – A: 0101 -> 101 But 0101 <> 101 in a signed system 0101 = +5 101 = -3 47

Sign Extension • Must “sign extend” B, • so B becomes 010 -> 0010 • Note: Value of B remains the same So 0101 (5) +0010 (2) Sign bit is extended -------0111 (7) 48

Sign Extension • • • What about negative numbers? Let A=0101 and B=100 Now B = 100 1100 0101 +1100 ------10001 Throw away Sign bit is extended (5) (-4) (1) 49

Why does sign extension work? • Note that: (− 1) = 1111 = 111… 1 – Thus, any number of leading 1’s is equivalent, so long as the leftmost one of them is implicitly negative. • Proof: 111… 1 = −(111… 1) = = −(100… 0 − 11… 1) = −(1) • So, the combined value of any sequence of leading ones is always just − 1 times the position value of the rightmost 1 in the sequence. 111… 100… 0 = (− 1)· 2 n n 50

Number Conversions 51

Decimal to Binary Conversion Method I: Use repeated subtraction. Subtract largest power of 2, then next largest, etc. Powers of 2: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2 n Exponent: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 , n 20 21 22 23 24 25 26 27 28 29 210 2 n 52

Decimal to Binary Conversion Suppose x = 156410 Subtract 1024: Subtract 512: 1564 -1024 (210) = 540 n=10 or 1 in the (210)’s position 540 -512 (29) = 28 n=9 or 1 in the (29)’s position 28=256, 27=128, 26=64, 25=32 > 28, so we have 0 in all of these positions Subtract 16: 28 -16 (24) = 12 n=4 or 1 in (24)’s position Subtract 8: Subtract 4: 12 – 8 (23) = 4 4 – 4 (22) = 0 n=3 or 1 in (23)’s position n=2 or 1 in (22)’s position Thus: 156410 = (1 1 0 0 1 1 1 0 0)2 53

Decimal to Binary Conversion Method II: Use repeated division by radix. 2 | 1564 2|__24_ 782 R=0 2|_____ 12 R=0 2|_____ 391 R=0 2|_____ 6 R=0 2|_____ 3 R= 0 195 R=1 2|_____ 1 R=1 97 R=1 2|_____ 48 R=1 0 R=1 24 R = 0 Collect remainders in reverse order 11000011100 54

Binary to Hex Conversion 1. Divide binary number into 4 -bit groups 01 1 0 0 1 1 1 0 0 Pad with 0’s If unsigned number 2. Substitute hex digit for each group Pad with sign bit if signed number 61 C 16 55

Hexadecimal to Binary Conversion Example 1. Convert each hex digit to equivalent binary (1 E 9 C)16 (0001 1110 1001 1100)2 56

Decimal to Hex Conversion Method II: Use repeated division by radix. 16 | 1564 97 16|_____ 6 16|_____ 0 R = 12 = C R=1 R=6 N = 61 C 16 57