Hoofdstuk 6 Discrete dynamische modellen differentievergelijking Ga naar

Hoofdstuk 6 Discrete dynamische modellen

differentievergelijking Ga naar het rijen invoerscherm van de GR en voer de rij in. Druk vervolgens op graph en dan op trace. Dit is de tijdgrafiek. Uit de plot van de grafiek kun je aflezen dat er inderdaad een grenswaarde is: De grenswaarde = 25 eerste

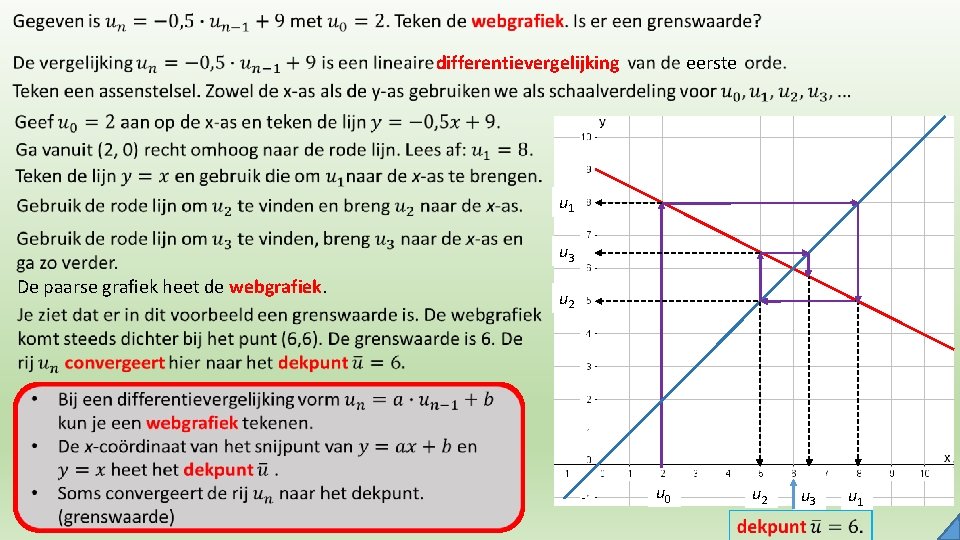
differentievergelijking eerste u 1 u 3 De paarse grafiek heet de webgrafiek. u 2 u 0 u 2 u 3 u 1

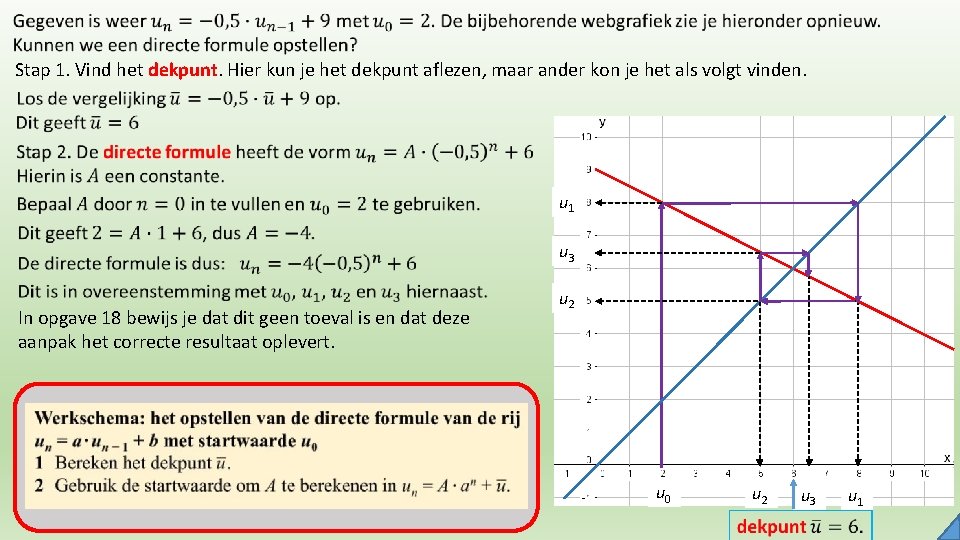
Stap 1. Vind het dekpunt. Hier kun je het dekpunt aflezen, maar ander kon je het als volgt vinden. u 1 u 3 In opgave 18 bewijs je dat dit geen toeval is en dat deze aanpak het correcte resultaat oplevert. u 2 u 0 u 2 u 3 u 1

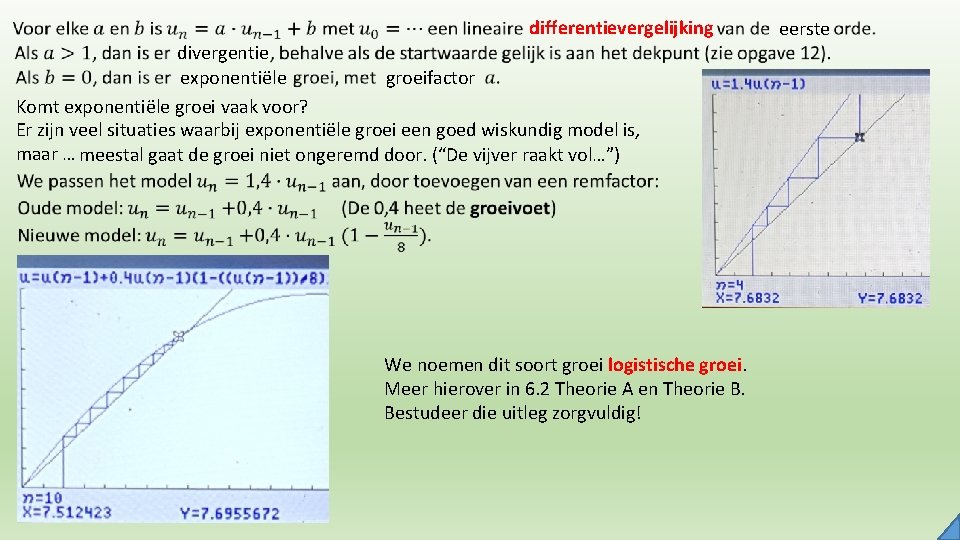
differentievergelijking divergentie groeifactor exponentiële Komt exponentiële groei vaak voor? Er zijn veel situaties waarbij exponentiële groei een goed wiskundig model is, maar … meestal gaat de groei niet ongeremd door. (“De vijver raakt vol…”) We noemen dit soort groei logistische groei. Meer hierover in 6. 2 Theorie A en Theorie B. Bestudeer die uitleg zorgvuldig! eerste

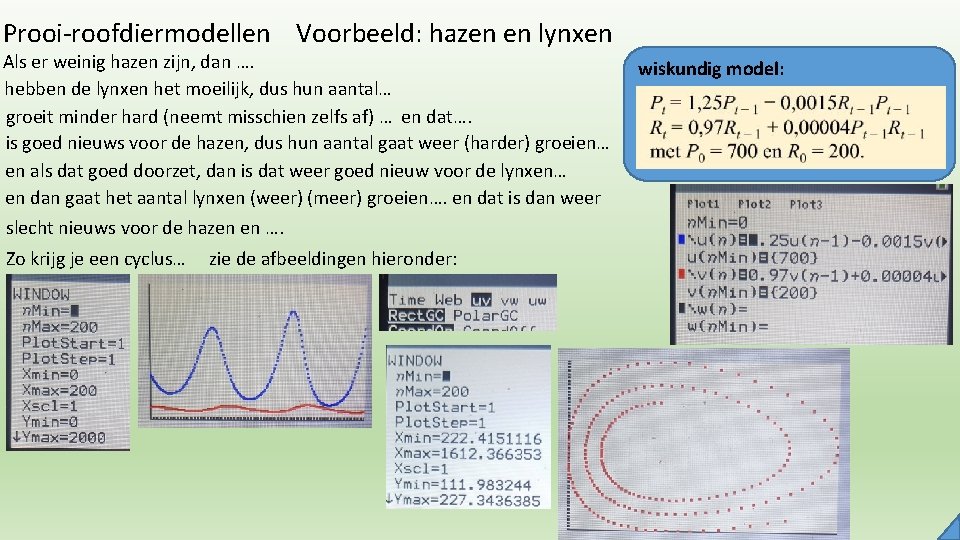
Prooi-roofdiermodellen Voorbeeld: hazen en lynxen Als er weinig hazen zijn, dan …. hebben de lynxen het moeilijk, dus hun aantal… groeit minder hard (neemt misschien zelfs af) … en dat…. is goed nieuws voor de hazen, dus hun aantal gaat weer (harder) groeien… en als dat goed doorzet, dan is dat weer goed nieuw voor de lynxen… en dan gaat het aantal lynxen (weer) (meer) groeien…. en dat is dan weer slecht nieuws voor de hazen en …. Zo krijg je een cyclus… zie de afbeeldingen hieronder: wiskundig model:

Een wiskundig model voor de verspreiding van griep bij een epidemie Soms is er een griepepidemie. Het is van belang daarvoor een passend wiskundig model te hebben. Natuurlijk blijft het een versimpeling van de werkelijkheid, maar zo’n model stelt ons in staat om voorspellingen te doen en daarvan gebruik te maken bij het maken van beleid …. Dorp met 2000 inwoners. We onderscheiden drie groepen: G (gezond maar niet immuun), Z (ziek), I (Immuun) Nu nog de beginaantallen vastleggen en ons model is klaar. Omdat het totale aantal van de drie groepen samen steeds gelijk blijft, spreken we van een gesloten systeem. Zie verder opgave 47, 48 en 49.

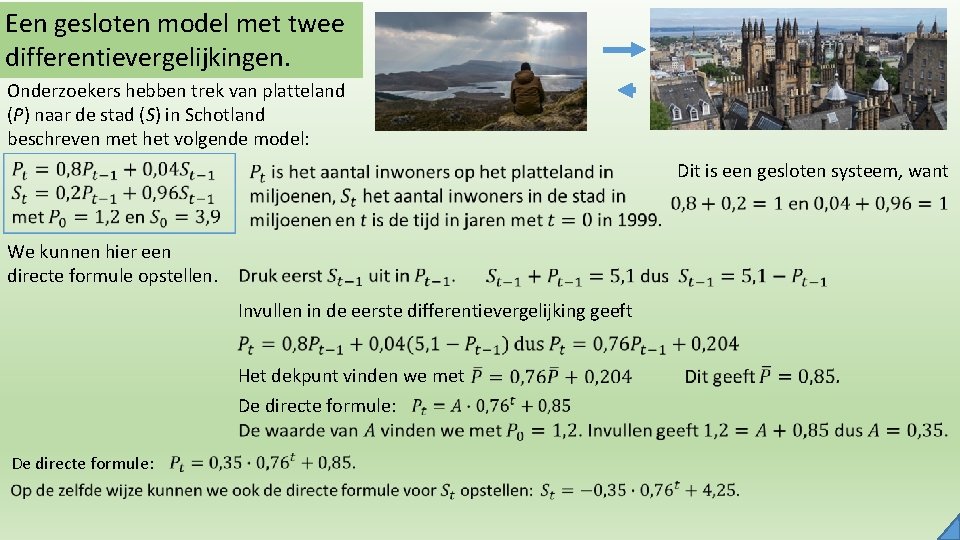
Een gesloten model met twee differentievergelijkingen. Onderzoekers hebben trek van platteland (P) naar de stad (S) in Schotland beschreven met het volgende model: Dit is een gesloten systeem, want We kunnen hier een directe formule opstellen. Invullen in de eerste differentievergelijking geeft Het dekpunt vinden we met De directe formule:

differentievergelijking eerste tweede e d e e Tw e! d r o Dit heet de karakteristieke vergelijking. In opgave 58 bewijs je dit!

We hebben gezien hoe je de directe formule opstelt bij een lineaire differentievergelijking van de tweede orde. Dit bewijs je in opgave 61! Dan heb je complexe getallen nodig om een directe formule op te stellen. Dat leer je volgend jaar!

Van een stelsel differentievergelijkingen naar een differentievergelijking van de tweede orde. Je kunt hieruit een lineaire differentiaalvergelijking van de tweede orde afleiden: Stap 1. Neem (1) en ga één stap in de tijd verder: Stap 2. Vul (2) hierin in. Stap 4. Neem (5) en ga weer één stap terug in de tijd: Nu heb je een lineaire differentievergelijking van de tweede orde en je zou bijvoorbeeld de karakteristieke vergelijking kunnen gebruiken om een directe formule op te stellen… (als startwaarden zijn gegeven). Zie ook het voorbeeld op bladzijde 91 van het boek.