Geometric scoring rules Egor Ianovski Aleksei Kondratev Alexander

Geometric scoring rules Egor Ianovski, Aleksei Kondratev, Alexander Nesterov (Higher School of Economics – St. Petersburg) April 2021 1

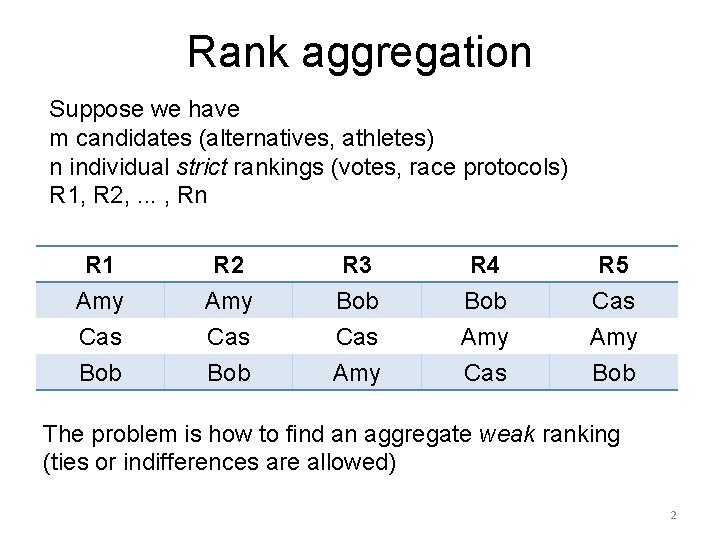
Rank aggregation Suppose we have m candidates (alternatives, athletes) n individual strict rankings (votes, race protocols) R 1, R 2, . . . , Rn R 1 Amy Cas Bob R 2 Amy Cas Bob R 3 Bob Cas Amy R 4 Bob Amy Cas R 5 Cas Amy Bob The problem is how to find an aggregate weak ranking (ties or indifferences are allowed) 2

Applications • Sports competitions • Elections • Meta-search engines • Group recommender systems • Genetics and computational biology 3

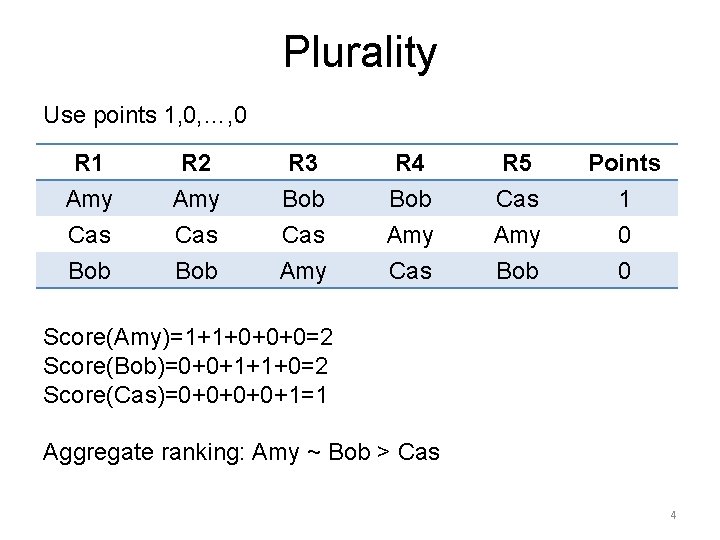
Plurality Use points 1, 0, …, 0 R 1 Amy Cas Bob R 2 Amy Cas Bob R 3 Bob Cas Amy R 4 Bob Amy Cas R 5 Cas Amy Bob Points 1 0 0 Score(Amy)=1+1+0+0+0=2 Score(Bob)=0+0+1+1+0=2 Score(Cas)=0+0+1=1 Aggregate ranking: Amy ~ Bob > Cas 4

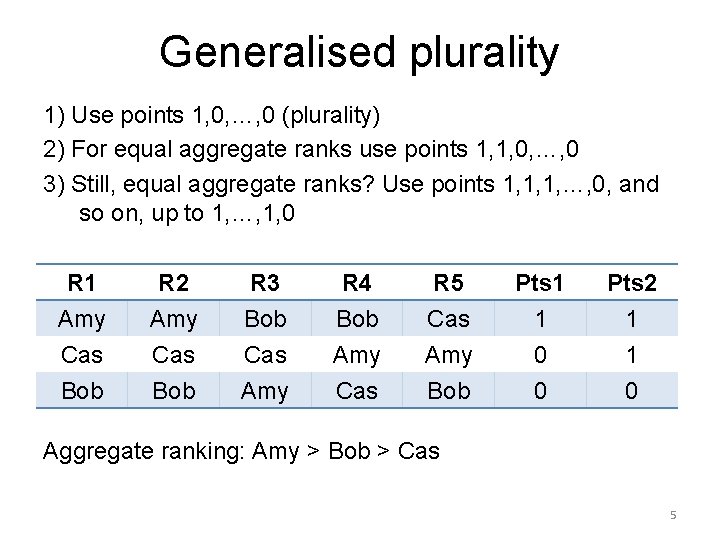
Generalised plurality 1) Use points 1, 0, …, 0 (plurality) 2) For equal aggregate ranks use points 1, 1, 0, …, 0 3) Still, equal aggregate ranks? Use points 1, 1, 1, …, 0, and so on, up to 1, …, 1, 0 R 1 Amy Cas Bob R 2 Amy Cas Bob R 3 Bob Cas Amy R 4 Bob Amy Cas R 5 Cas Amy Bob Pts 1 1 0 0 Pts 2 1 1 0 Aggregate ranking: Amy > Bob > Cas 5

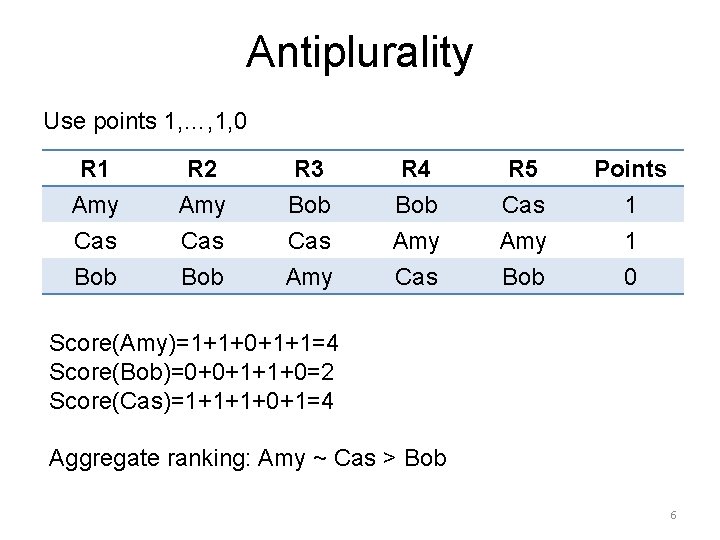
Antiplurality Use points 1, …, 1, 0 R 1 Amy Cas Bob R 2 Amy Cas Bob R 3 Bob Cas Amy R 4 Bob Amy Cas R 5 Cas Amy Bob Points 1 1 0 Score(Amy)=1+1+0+1+1=4 Score(Bob)=0+0+1+1+0=2 Score(Cas)=1+1+1+0+1=4 Aggregate ranking: Amy ~ Cas > Bob 6

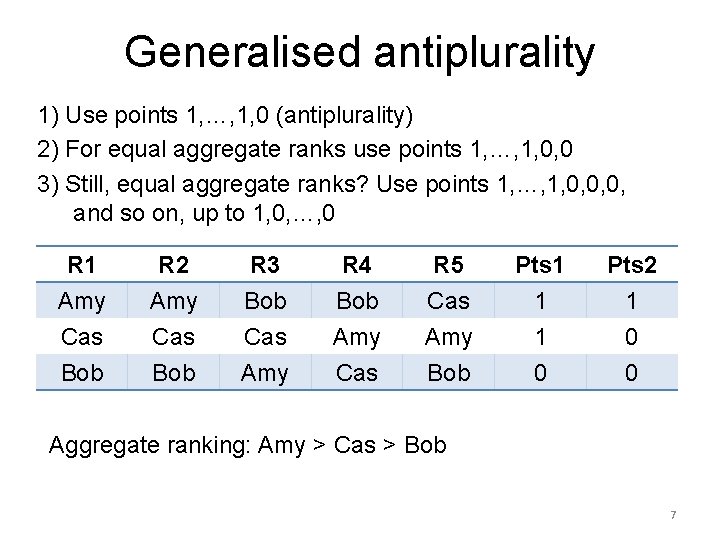
Generalised antiplurality 1) Use points 1, …, 1, 0 (antiplurality) 2) For equal aggregate ranks use points 1, …, 1, 0, 0 3) Still, equal aggregate ranks? Use points 1, …, 1, 0, 0, 0, and so on, up to 1, 0, …, 0 R 1 Amy Cas Bob R 2 Amy Cas Bob R 3 Bob Cas Amy R 4 Bob Amy Cas R 5 Cas Amy Bob Pts 1 1 1 0 Pts 2 1 0 0 Aggregate ranking: Amy > Cas > Bob 7

Borda Use points m-1, m-2, …, 1, 0 R 1 Amy Cas Bob R 2 Amy Cas Bob R 3 Bob Cas Amy R 4 Bob Amy Cas R 5 Cas Amy Bob Points 2 1 0 Score(Amy)=2+2+0+1+1=6 Score(Bob)=0+0+2+2+0=4 Score(Cas)=1+1+1+0+2=5 Aggregate ranking: Amy > Cas > Bob 8

Scoring rules A scoring rule is a family of non-increasing vectors for each m: – s 1, s 2, …, sm-1, sm for m candidates – t 1, t 2, …, tm-1 for m-1 candidates, and so on • Borda: – 1, 0 – 2, 1, 0 – m-1, m-2, …, 1, 0 • Plurality: – 1, 0, …, 0 • Antiplurality: – 1, …, 1, 0 for 2 candidates for 3 candidates for m candidates 9

Advantages of scoring rules Simple and clear Smith (1973), Young (1975) Only generalized scoring rules satisfy: Anonymity Neutrality Electoral consistency Apesteguia, Ballester, Ferrer (2011), Boutilier et al (2012, 2015) Maximize utility Main problem How should we choose a concrete vector of points? 10

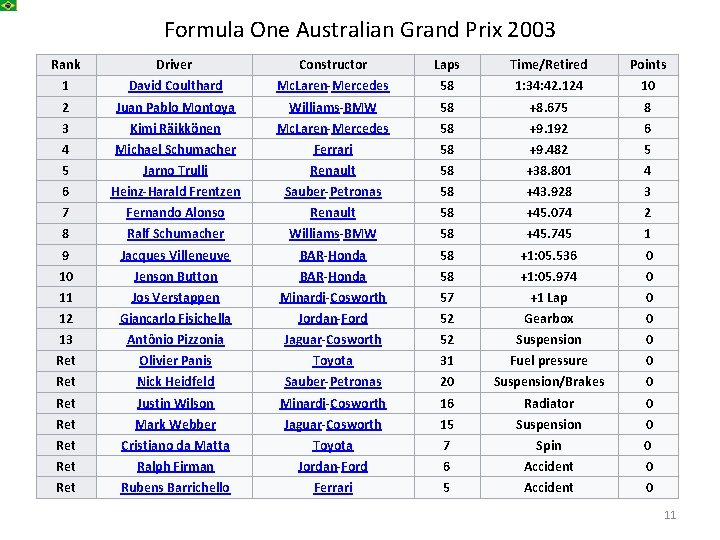
Formula One Australian Grand Prix 2003 Rank Driver Constructor Laps Time/Retired Points 1 David Coulthard Mc. Laren-Mercedes 58 1: 34: 42. 124 10 2 Juan Pablo Montoya Williams-BMW 58 +8. 675 8 3 Kimi Räikkönen Mc. Laren-Mercedes 58 +9. 192 6 4 Michael Schumacher Ferrari 58 +9. 482 5 5 Jarno Trulli Renault 58 +38. 801 4 6 Heinz-Harald Frentzen Sauber-Petronas 58 +43. 928 3 7 Fernando Alonso Renault 58 +45. 074 2 8 Ralf Schumacher Williams-BMW 58 +45. 745 1 9 Jacques Villeneuve BAR-Honda 58 +1: 05. 536 0 10 Jenson Button BAR-Honda 58 +1: 05. 974 0 11 Jos Verstappen Minardi-Cosworth 57 +1 Lap 0 12 Giancarlo Fisichella Jordan-Ford 52 Gearbox 0 13 Antônio Pizzonia Jaguar-Cosworth 52 Suspension 0 Ret Olivier Panis Toyota 31 Fuel pressure 0 Ret Nick Heidfeld Sauber-Petronas 20 Suspension/Brakes 0 Ret Justin Wilson Minardi-Cosworth 16 Radiator 0 Ret Mark Webber Jaguar-Cosworth 15 Suspension 0 Ret Cristiano da Matta Toyota 7 Spin 0 Ret Ralph Firman Jordan-Ford 6 Accident 0 Ret Rubens Barrichello Ferrari 5 Accident 0 11

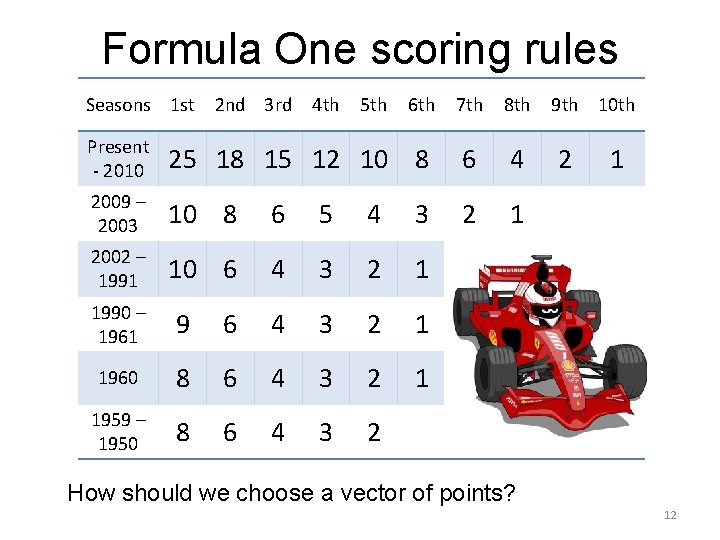
Formula One scoring rules Seasons 1 st 2 nd 3 rd 4 th 5 th 6 th 7 th 8 th Present - 2010 25 18 15 12 10 8 6 4 2009 – 2003 10 8 6 5 4 3 2 1 2002 – 1991 10 6 4 3 2 1 1990 – 1961 9 6 4 3 2 1 1960 8 6 4 3 2 1 1959 – 1950 8 6 4 3 2 9 th 10 th 2 1 How should we choose a vector of points? 12

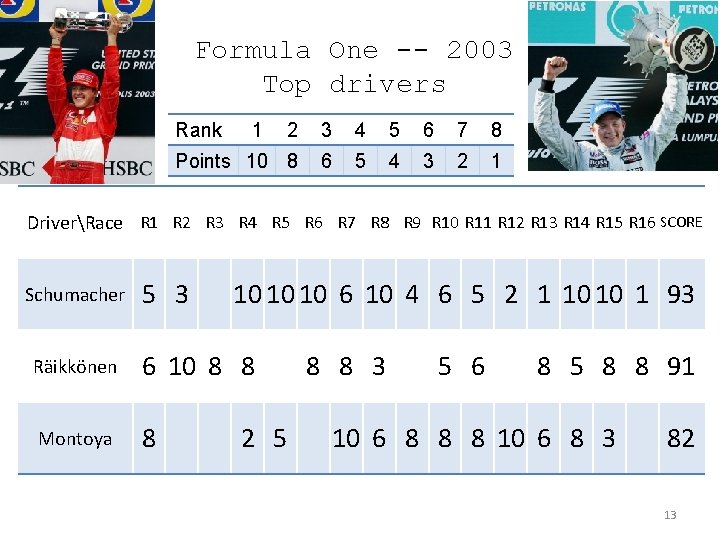
Formula One -- 2003 Top drivers Rank 1 2 3 4 5 6 7 8 Points 10 8 6 5 4 3 2 1 DriverRace R 1 R 2 R 3 R 4 R 5 R 6 R 7 R 8 R 9 R 10 R 11 R 12 R 13 R 14 R 15 R 16 SCORE Schumacher 5 3 10 10 10 6 10 4 6 5 2 1 10 10 1 93 Räikkönen 6 10 8 8 Montoya 8 2 5 8 8 3 5 6 8 5 8 8 91 10 6 8 8 8 10 6 8 3 82 13

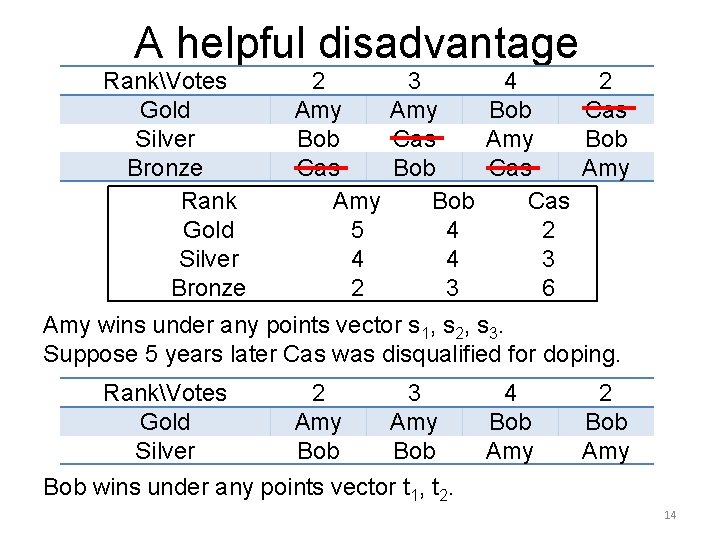
A helpful disadvantage RankVotes Gold Silver Bronze Rank Gold Silver Bronze 2 3 4 2 Amy Bob Cas Amy Amy Bob Cas 5 4 2 4 4 3 2 3 6 Amy wins under any points vector s 1, s 2, s 3. Suppose 5 years later Cas was disqualified for doping. RankVotes 2 3 Gold Amy Silver Bob Bob wins under any points vector t 1, t 2. 4 Bob Amy 2 Bob Amy 14

Arrow’s theorem Theorem (Arrow, 1950, 1963): For 3 or more alternatives, a rank aggregation rule satisfies: weak unanimity, independence of irrelevant alternatives, if and only if it is a Dictatorial rule Remark: Using this theorem, one can prove that the paradox from the previous slide is inevitable. 15

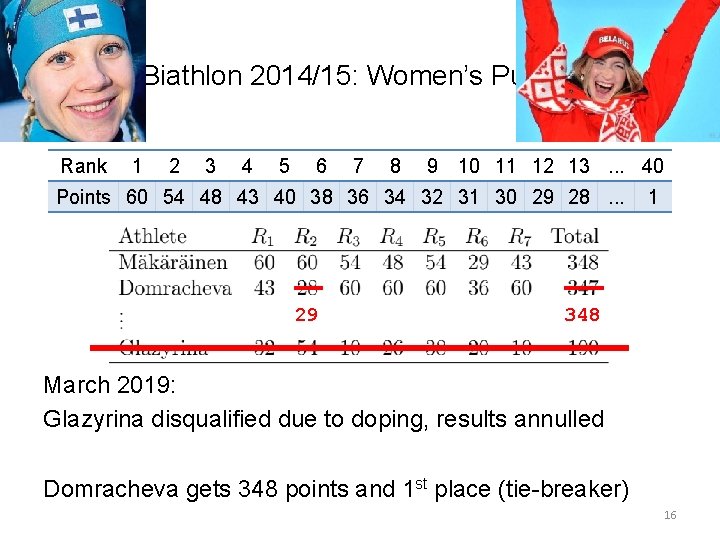
Biathlon 2014/15: Women’s Pursuit Rank 1 2 3 4 5 6 7 8 9 10 11 12 13. . . 40 Points 60 54 48 43 40 38 36 34 32 31 30 29 28. . . 29 1 348 March 2019: Glazyrina disqualified due to doping, results annulled Domracheva gets 348 points and 1 st place (tie-breaker) 16

Impossibilities • Independence of irrelevant alternatives requires dictatorship (Arrow, 1950, 1963) • Independence of winners/losers requires Kemeny-Young method (Kemeny, 1959; Young, 1988) • Scoring rules fail independence of winners/losers: – Profile R=(R 1, R 2, …, Rn), scores S=(s 1, s 2, …, sm), T=(t 1, t 2, …, tm-1) – For each scores S, T there is profile R such that removing one athlete inverts the final ranking (Fishburn, 1980) 17

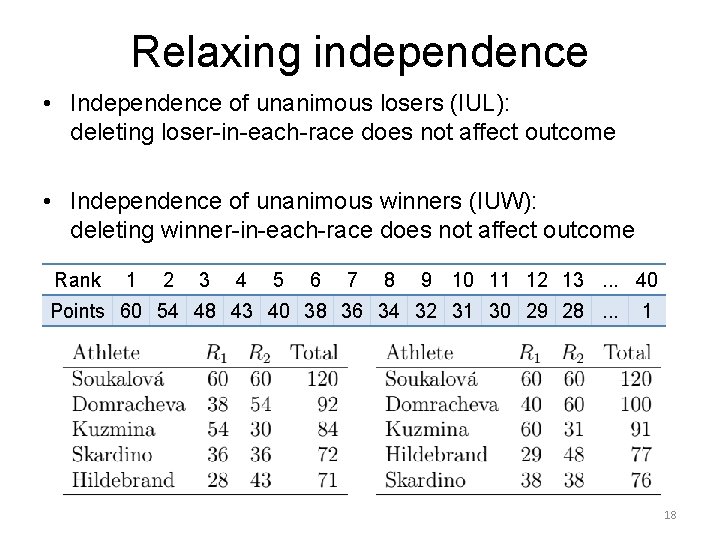
Relaxing independence • Independence of unanimous losers (IUL): deleting loser-in-each-race does not affect outcome • Independence of unanimous winners (IUW): deleting winner-in-each-race does not affect outcome Rank 1 2 3 4 5 6 7 8 9 10 11 12 13. . . 40 Points 60 54 48 43 40 38 36 34 32 31 30 29 28. . . 1 18

Linear equivalence Suppose we have Borda’s rule: – 3, 2, 1, 0 (for m=4 candidates) Multiply e. g. by 3: – 9, 6, 3, 0 (for m=4 candidates) – Does it change aggregate ranking? – No! Add e. g. -2: – 7, 4, 1, -2 (for m=4 candidates) – Does it change aggregate ranking? – No! Scoring vectors Sm and Tm are equivalent if for a>0: Sm = a × T m + b 19

Which scoring rules satisfy IUL, IUW? Consider scores Sm and Tm-1: – s 1, s 2, …, sm-1, sm (for m candidates) – t 1, t 2, …, tm-1 (for m-1 candidates) Lemma (Kondratev, Ianovski, Nesterov, 2019): scores Sm and Tm-1 satisfy independence of unanimous losers <=> t 1, t 2, …, tm-1 and s 1, s 2, …, sm-1 are linearly equivalent unanimous winners <=> t 1, t 2, …, tm-1 and s 2, s 3, …, sm are linearly equivalent 20

Geometric scoring rules Theorem (Kondratev, Ianovski, Nesterov, 2019): a scoring rule satisfies IUL and IUW if and only if there is p>0 such that S = pm-1, pm-2, . . . , 1, p>1 m-1, m-2, . . . , 0, p=1 1 -pm-1, 1 -pm-2, . . . , 0, p<1 (S = 1+p+p 2+…+pm-2, …, 1+p+p 2, 1+p, 1, 0) 21

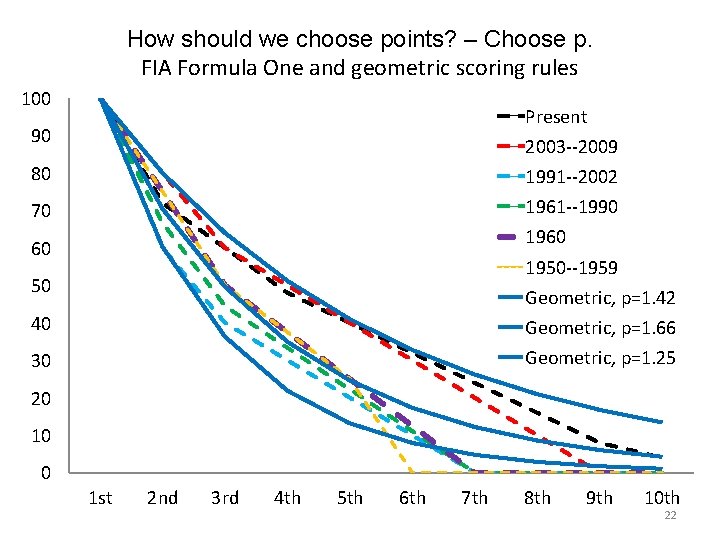
How should we choose points? – Choose p. FIA Formula One and geometric scoring rules 100 Present 90 2003 --2009 80 1991 --2002 70 1961 --1990 1960 60 1950 --1959 50 Geometric, p=1. 42 40 Geometric, p=1. 66 30 Geometric, p=1. 25 20 10 0 1 st 2 nd 3 rd 4 th 5 th 6 th 7 th 8 th 9 th 10 th 22

Extreme cases Geometric scores 1+p+p 2+…+pm-2, …, 1+p+p 2, 1+p, 1, 0 What do we have when the number of voters is fixed but p infinity? – Generalized plurality! (lexicographical voting rule, medal count ranking). Bernie Ecclestone, the chief executive of the Formula One Group, in 2009 proposed to use medal count. P 0? – Generalized antiplurality! Group recommender systems use it (Masthoff, 2015): e. g. , POLYLENS (movies) and REMPAD (multimedia to use in group reminiscence therapy). 23

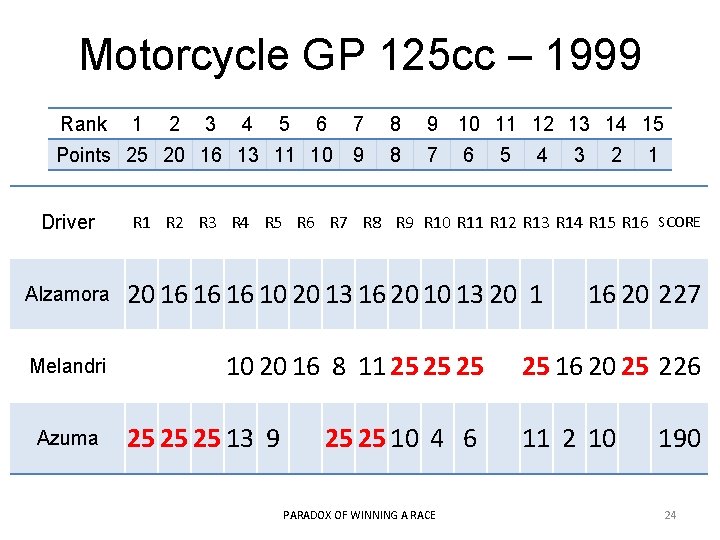
Motorcycle GP 125 cc – 1999 Rank 6 7 8 9 10 11 12 13 14 15 Points 25 20 16 13 11 10 9 8 7 6 Driver Alzamora Melandri Azuma 1 2 3 4 5 5 4 3 2 1 R 2 R 3 R 4 R 5 R 6 R 7 R 8 R 9 R 10 R 11 R 12 R 13 R 14 R 15 R 16 SCORE 20 16 16 16 10 20 13 16 20 10 13 20 1 10 20 16 8 11 25 25 25 13 9 25 25 10 4 6 PARADOX OF WINNING A RACE 16 20 227 25 16 20 25 226 11 2 10 190 24

Paradox of winning a race In 2009, Bernie Ecclestone, the former chief executive of the Formula One Group, was outspoken about similar issues in Formula One – “It’s just not on that someone can win the world championship without winning a race. ” Instead of the scores then used, Ecclestone proposed a medal system which is equivalent to generalised plurality Fact (Kondratev, Ianovski, Nesterov, 2019): A geometric scoring rule is invulnerable to the winning a race paradox if and only if it is generalised plurality. 25

Majority winner is a candidate that finishes first in more than half of individual races. Theorem (Lepelley, 1992; Sanver, 2002): A scoring rule always ranks a majority winner first in the aggregate ranking if and only if it is plurality. Theorem (Kondratev, Ianovski, Nesterov, 2019): A generalized scoring rule satisfies independence of unanimous winners and always ranks a majority winner first in the aggregate ranking if and only if it is generalized plurality. 26

Majority loser is a candidate that finishes last in more than half of individual races. Theorem (Kondratev, Ianovski, Nesterov, 2019): A generalized scoring rule satisfies independence of unanimous losers and always ranks a majority loser last in the aggregate ranking if and only if it is generalized antiplurality. 27

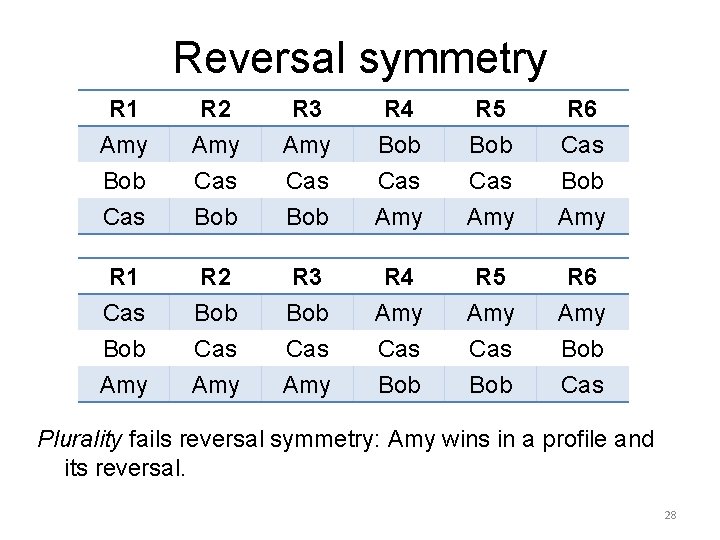
Reversal symmetry R 1 Amy Bob Cas R 2 Amy Cas Bob R 3 Amy Cas Bob R 4 Bob Cas Amy R 5 Bob Cas Amy R 6 Cas Bob Amy R 1 Cas Bob Amy R 2 Bob Cas Amy R 3 Bob Cas Amy R 4 Amy Cas Bob R 5 Amy Cas Bob R 6 Amy Bob Cas Plurality fails reversal symmetry: Amy wins in a profile and its reversal. 28

Reversal symmetry: a candidate cannot be first in the aggregate ranking for a profile and for the reversal profile (Saari, 1994). Theorem (Kondratev, Ianovski, Nesterov, 2019): A scoring rule satisfies independence of unanimous losers and reversal symmetry if and only if it is Borda. A scoring rule satisfies independence of unanimous winners and reversal symmetry if and only if it is Borda. 29

Conclusions • Independence of unanimous winners and losers gives one-parameter geometric family that includes: – convex rules (good for competitions) – concave rules (good for group recommendations) – popular rules: Borda, plurality, antiplurality • Only 1 degree of freedom (instead of m-2) • The first characterization of a family (using natural and desirable axioms) • Elegant characterizations of Borda, generalized plurality and generalised antiplurality • What is next? – We revise our manuscript, developing an optimization approach and its empirical evaluation for how to choose the parameter p. 30