General Considerations u Nonlinear not linear x not

General Considerations u Nonlinear • not linear (x) • not necessarily linear (o) u Why study nonlinear system ? • All physical systems are nonlinear in nature. • Nonlinearities may be introduced intentionally into a system in order to compensate for the effect of other undesirable nonlinearities, or to obtain better performance (on-off controller). u Linear system closed form solution Nonlinear system X closed form solution (Some predictions – qualitative analysis) 1 -1

1. Phenomena of Nonlinear Dynamics u Linear vs. Nonlinear Input Output System state, Definitions : Linear : when the superposition holds Nonlinear : otherwise 1 -2

Stability & Output of systems • Stability depends on the system’s parameter (linear) • Stability depends on the initial conditions, input signals as well as the system parameters (nonlinear). • Output of a linear system has the same frequency as the input although its amplitude and phase may differ. • Output of a nonlinear system usually contains additional frequency components and may, in fact, not contain the input frequency. 1 -3

Superposition * Superposition Sys. = Sys. Is (1) linear ? + So is it linear? No, under zero initial conditions only. 1 -4

Linearity What is the linearity when ? + A mnemonic rule: All functions in RHS of a differential equation are linear. System is linear atleast at zero input or zero initial condition Ex: 1 -5

Time invariant vs. Time varying u Time invariant vs. Time varying • System (1) is time invariant parameters are constant - Linear time varying system • System (2) is time invariant no function has t as its argument. - Nonlinear time varying system 1 -6

Autonomous & Non - Autonomous • Time invariant system are called autonomous and time varying are called non - autonomous. In this course, ‘autonomous’ is reserved for systems with no external input, i. e. , Ex: • Thus autonomous are time invariant systems with no external input. This course will address nonlinear system, both time invariant and time varying, but mostly autonomous. 1 -7

Equilibrium Point u Equilibrium Point • We start with an autonomous system. Definition: is an equilibrium point (or a steady state, or a singular point) If det(A) 0, (1)has a unique equilibrium point, (Linear System). Nonlinear system ? × × × multiple equilibrium points 1 -8

Linear Autonomous Systems u What can a linear autonomous system do? where For 1 -dim sys. For 2 -dim sys. 1 -9

Linear Autonomous Systems (Contd. ) 1 -10

Solution of Linear systems • For linear sys, the following facts are true u Solution always exists locally. u Solution always exists globally. u Solution is unique each initial condition produces a different trajectory. u Solution is continuously dependent on initial conditions for every finite t, u Equilibrium point is unique (when det A 0). 1 -11

Periodic Solution • If there is one periodic solution, there is an infinite set of periodic solutions. (There is no isolated closed solution. ) Ex: ( many periodic solutions, w. r. t. I. C. ) 1 -12

Non - linear Autonomous System u What can a nonlinear autonomous system do ? Basically everything. • A solution may not exist, even locally. Here the solution is chattering, because function satisfying the equation exists. Therefore, no differential 1 -13

Solutions • Solution may not exist globally. Assume finite escape time (= : linear system) • Solution may not be unique. 1 -14

Equilibrium point • Equilibrium point doesn’t have to be unique. Ex: 1 -15

Periodic Solutions • Nonlinear system may have isolated closed (periodic) solutions. Ex: 1 -16

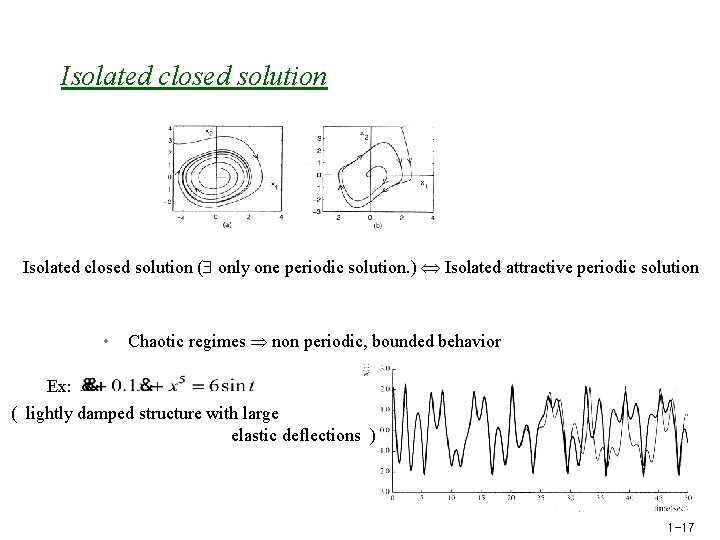
Isolated closed solution ( only one periodic solution. ) Isolated attractive periodic solution • Chaotic regimes non periodic, bounded behavior Ex: ( lightly damped structure with large elastic deflections ) 1 -17

2. Second Order Systems u Isoclines called “vector field” Set of all trajectories on plane Phase portrait 1 -18

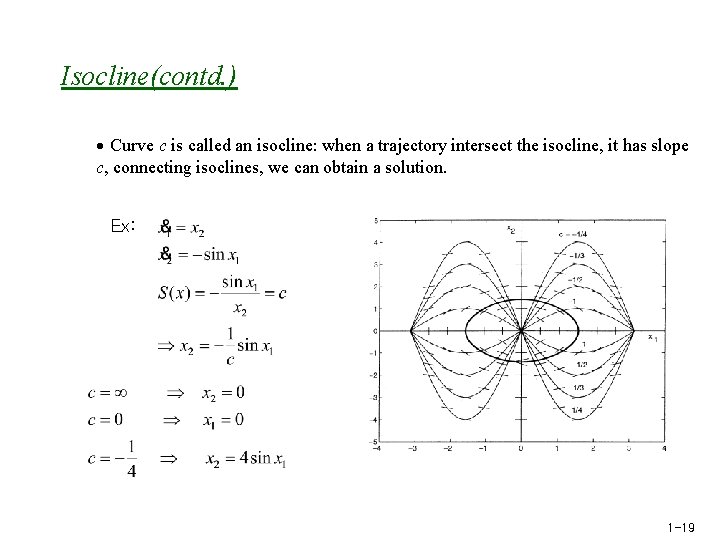
Isocline(contd. ) Curve c is called an isocline: when a trajectory intersect the isocline, it has slope c, connecting isoclines, we can obtain a solution. Ex: 1 -19

Linearization u Linearization A nonlinear system can be represented as a bunch of linear systems - each valid in a small neighborhood of using linearization. Specifically, assume that is continuously, differentiable, Take one of the equilibrium, say Introduce, where =0 1 -20

Linearization(contd. ) Consider a sufficiently small ball The linearization of at around is defined by Ex: 1 -21

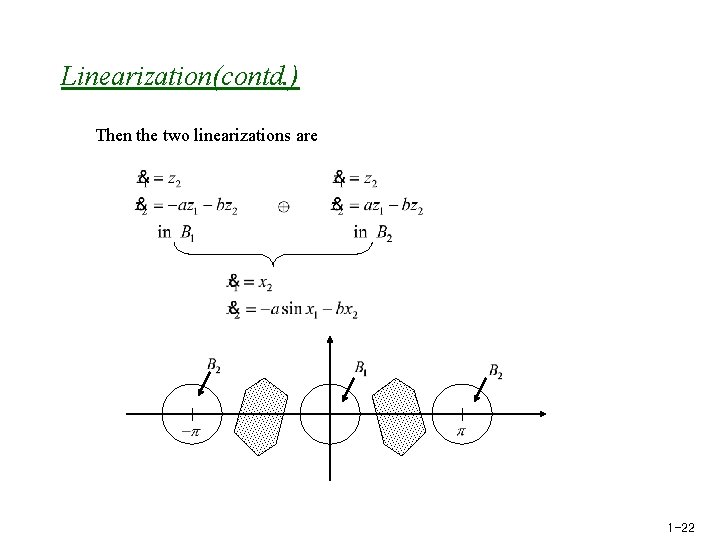
Linearization(contd. ) Then the two linearizations are 1 -22

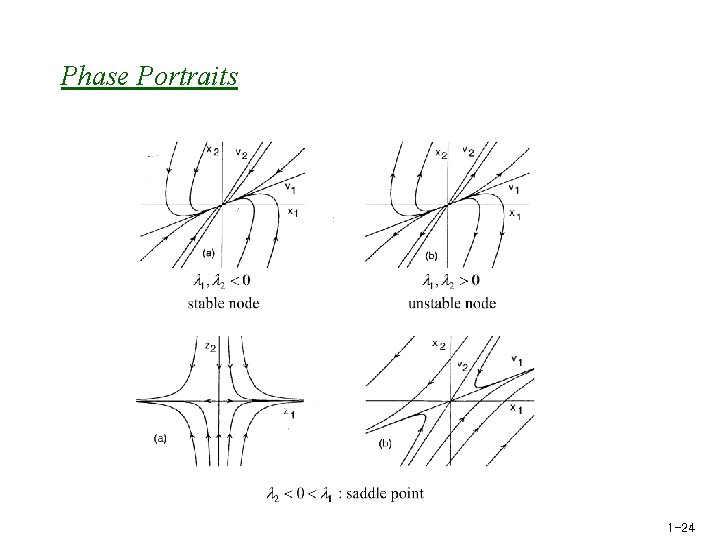
Singular Points u Nature of singular points (a) 1 -23

Phase Portraits 1 -24

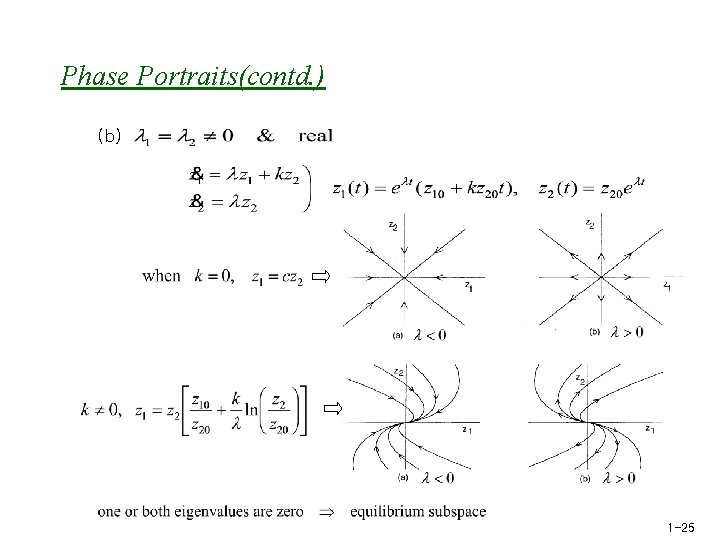
Phase Portraits(contd. ) (b) 1 -25

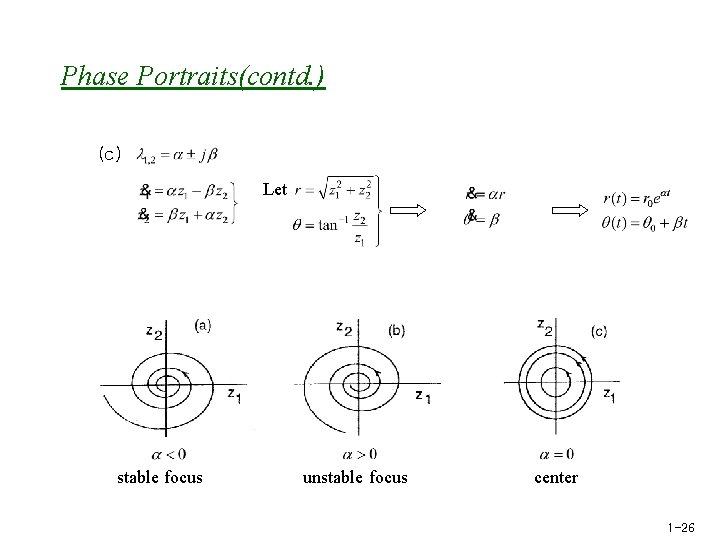
Phase Portraits(contd. ) (c) Let stable focus unstable focus center 1 -26

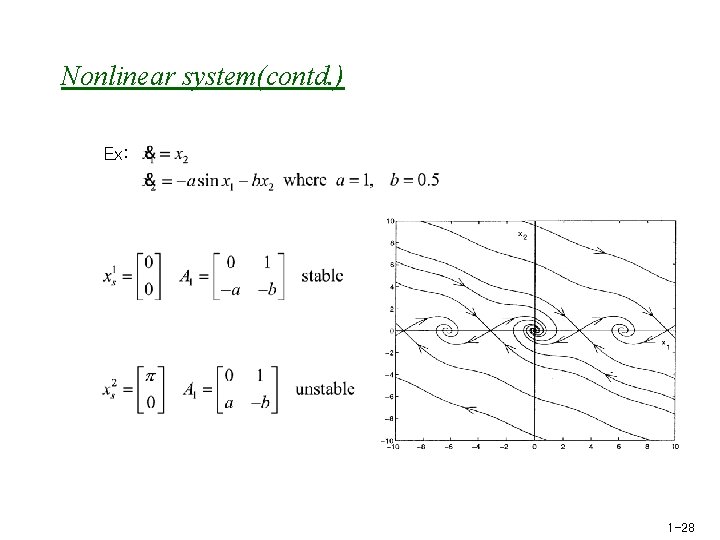
Nonlinear system u Nonlinear system Assume that the nature of this singular point in the linear system is What is the nature of the singular point in the nonlinear system ? Ans) Same, except for center. Center for the linear system doesn’t mean center in the nonlinear system. Equilibrium of a nonlinear system such that the linearization has no eigenvalues on the imaginary axis is called hyperbolic. Thus, for hyperbolic equilibria, the nature is the same as the linearization. 1 -27

Nonlinear system(contd. ) Ex: 1 -28