Jeopardy Linear Nonlinear Systems 2 Variable Linear Systems

Jeopardy Linear & Nonlinear Systems 2 -Variable Linear Systems Multivariable Partial Linear Fraction Systems Decomposition $100 $100 $200 $200 $300 $300 $400 $400 $500 $500 Final Jeopardy Systems of Inequalities

Linear/Nonlinear Systems - $100 n (d) (-1/2, -3)

Linear/Nonlinear Systems - $200 n (2, 2)

Linear/Nonlinear Systems - $300 n (0, -5), (4, 3)

Linear/Nonlinear Systems - $400 Find the sales necessary to break even (R=C) for the cost C of producing x units and the revenue R obtained by selling x units. (Round to the nearest whole unit. ) n C = 8650 x + 250, 000 n R = 9950 x n n 192 units

Linear/Nonlinear Systems - $500 n (2, 2. 5)

2 Variable Linear Systems - $100 (2, 1)

2 Variable Linear Systems - $200 n No Solution

2 Variable Linear Systems - $300 n (4, 1)

2 Variable Linear Systems - $400 n One 8 oz glass of apple juice and one 8 oz glass of orange juice contain a total of 185 mg of Vitamin C. Two 8 oz glasses of apple juice and three 8 oz glasses of orange juice contain a total of 452 mg of Vitamin C. How much Vitamin C is in an 8 oz glass of each type of juice? Apple Juice – 103 mg n Orange Juice – 82 mg n

2 Variable Linear Systems - $500 n An airplane flew 4 hours with a 25 mph tail wind. The return trip against the same wind took 5 hours. Find the speed of the airplane in still air. n 225 miles per hour

Multi. Variable Systems - $100 (d) (-1, 0, 4)

Multi. Variable Systems - $200 n (1, -2, 4)

Multi. Variable Systems - $300

Multi. Variable Systems - $400 n A florist is creating 10 centerpieces for a wedding. The florist can use: roses ($2. 50 ea), lilies ($4 ea) and irises ($2 ea). The customer has a budget of $300 and wants each bouquet to contain 12 flowers with twice as many roses used as the other two types of flowers combined. How many of each type of flower should be used in each centerpiece? n Roses = 8, Lilies = 1, Irises = 3

Multi. Variable Systems - $500 n Find the equation of the parabola y=ax 2+bx+c passing through the points (0, 6), (-2, 2), & (3, 9/2) n y=-1/2 x 2+ x + 6

Partial Fractions - $100 n If the degree of the numerator of rational expression is greater than or equal to the degree of the denominator, what procedure do you follow to decompose the fraction? n Perform polynomial long division and decompose the remainder

Partial Fractions - $200

Partial Fractions - $300

Partial Fractions - $400

Partial Fractions - $500 n False

Inequalities/Linear Prog - $100 n An ordered pair, (a, b) is a ______ of an inequality in x and y if the inequality is true when a and b are substituted for x and y, respectively. n Solution

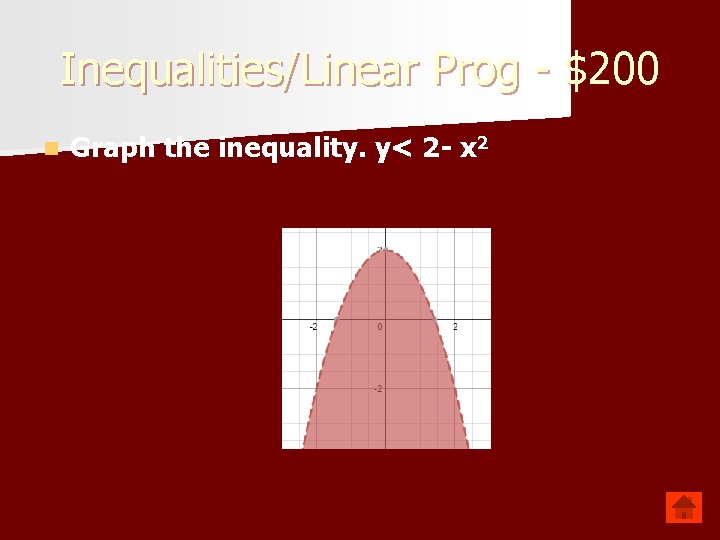
Inequalities/Linear Prog - $200 n Graph the inequality. y< 2 - x 2

Inequalities/Linear Prog - $300 n (c) (-4, 0)

Inequalities/Linear Prog - $400 Min = (36, 0): 36 n Max = (24, 8): 56 n

Inequalities/Linear Prog - $500 n A shoe manufacturer produces a walking shoe and a running shoe, yielding profits of $18 and $24, respectively. Each shoe must go through 3 processes for which the required times are shown in this table. What is the optimal production level for each shoe, that produces max profit? What is max profit? Process 1 2 3 Hours for walking shoe 4 1 1 Hours for running shoe 2 2 1 Hours available per day 24 9 8 n n n 5 walking shoes 2 running shoes Optimal Profit = $138