Computing Longest Common SubstringSubsequence of Nonlinear Texts Kouji

Computing Longest Common Substring/Subsequence of Non-linear Texts Kouji Shimohira, Shunsuke Inenaga, Hideo Bannai, Masayuki Takeda Kyushu University, Japan

Outline �Non-linear Text �Computing Longest Common Subsequence of Acyclic Non-linear Texts �Computing Longest Common Subsequence of Cyclic Non-linear Texts �Conclusions and Future works

Non-linear Text G = ( V , E , L ） A directed graph with vertices labeled by characters. V : the set of vertices. E : the set of arcs. L : V → Σ ： a labeling function. e. g. V = ｛ v 1 , v 2 , v 3 , v 4 , v 5 , v 6 , v 7 , v 8 , v 9 ｝ E = ｛(v 1, v 2), (v 2, v 3), (v 2, v 7), (v 3, v 4), (v 4, v 5), (v 5, v 6), (v 6, v 7), (v 6, v 8), (v 7, v 8), (v 8, v 9)｝ L = ｛ v 1 → a, v 2 → b, v 3 → c, v 4 → a, v 5 → a, v 6 → b, v 7 → b, v 8 → a, v 9 → c ｝ G a c 1 b 3 a a 4 5 b 6 a 2 b 7 8 c 9

Non-linear Text L(v) : the character label of vertex v P(v) : the set of paths that end at vartex v. L(P(v)) : the set of strings spelled by paths in P(v) P(G) : the set of paths in G. ( P(G) = {P(v) | v∈V } ) L(P(G)) : the set of strings spelled by paths in P(G) (= L(G)) substr(L(G)) : the set of substrings of strings in L(G) subseq(L(G)) : the set of subseqences of strings in L(G) e. g. G’ a c 1 b 3 a a 4 5 b L(v７) = b 6 a 2 b 7 P(v７) = {v 1 v 2 v 3 v 4 v 5 v 6 v 7 , v 1 v 2 v 7 } 8 c 9 L(P(v７)) = {abcaabb , abb } bcaa ∈ substr(L(G)) aca ∈ subseq(L(G))

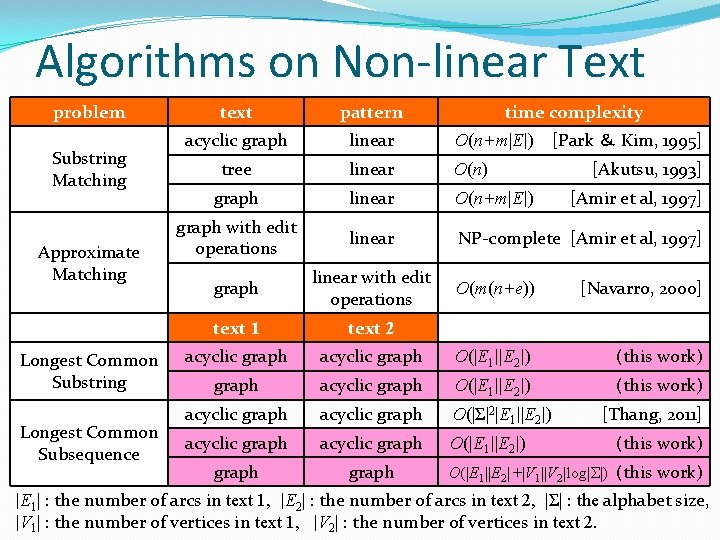
Algorithms on Non-linear Text problem Substring Matching Approximate Matching Longest Common Substring Longest Common Subsequence text pattern time complexity acyclic graph linear O(n+m|E|) tree linear O(n) graph linear O(n+m|E|) graph with edit operations linear NP-complete [Amir et al, 1997] graph linear with edit operations text 1 text 2 acyclic graph [Park ＆ Kim, 1995] [Akutsu, 1993] [Amir et al, 1997] O(m(n+e)) [Navarro, 2000] acyclic graph O(|E 1||E 2|) (this work) graph acyclic graph O(|E 1||E 2|) (this work) acyclic graph O(|Σ|2|E 1||E 2|) acyclic graph O(|E 1||E 2|) graph [Thang, 2011] (this work) O(|E 1||E 2|+|V 1||V 2|log|Σ|) (this work) |E 1| : the number of arcs in text 1, |E 2| : the number of arcs in text 2, |Σ| : the alphabet size, |V 1| : the number of vertices in text 1, |V 2| : the number of vertices in text 2.

Outline �Non-linear Text �Computing Longest Common Subsequence of Acyclic Non-linear Texts �Computing Longest Common Subsequence of Cyclic Non-linear Texts �Conclusions and Future works

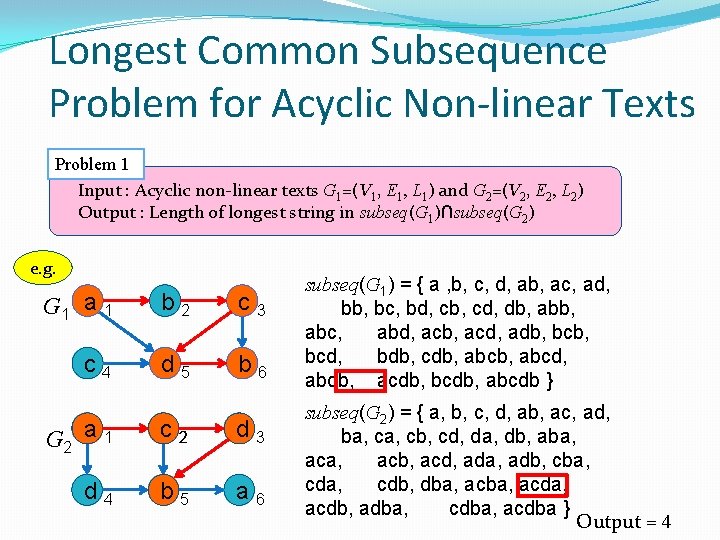
Longest Common Subsequence　 Problem for Acyclic Non-linear Texts Problem 1 　Input : Acyclic non-linear texts G 1=(V 1, E 1, L 1) and G 2=(V 2, E 2, L 2) 　Output : Length of longest string in subseq(G 1)∩subseq(G 2) e. g. G 1 a 1 b 2 c 3 c 4 d 5 b 6 G 2 a 1 c 2 d 3 d 4 b 5 a 6 subseq(G 1) = { a , b, c, d, ab, ac, ad, bb, bc, bd, cb, cd, db, abc, abd, acb, acd, adb, bcd, bdb, cdb, abcd, abdb, acdb, bcdb, abcdb } subseq(G 2) = { a, b, c, d, ab, ac, ad, ba, cb, cd, da, db, aba, acb, acd, ada, adb, cba, cdb, dba, acda, acdb, adba, cdba, acdba } Output = 4

Algorithm 1 : Computing the length of longest common subsequence of acyclic non-linear texts Sort vertices of G 1 and G 2 in topological order Let C be a |V 1|×|V 2| integer table (Ci, j : the length of a longest string in subseq(P(v 1, i))∩subseq(P(v 2, j)) Compute Ci, j using dynamic programing for all 1≦ i ≦ |V 1| and 1≦ j ≦ |V 2| Return max Ci, j

Topological Sort vertices of G 1 and G 2 in topological order G 1 a 1 b 2 c 3 c 4 d 5 b 6 G 2 a 1 c 2 d 3 d 4 b 5 a 6 G 1 a 1 b 2 c 3 c 4 d 5 b 6 sort v 1, 1 v 1, 2 v 1, 3 v 1, 4 v 1, 5 v 1, 6 G 2 a 1 c 2 d 3 d 4 b 5 b 6 v 2, 1 v 2, 2 v 2, 3 v 2, 4 v 2, 5 v 2, 6

Dynamic Programing table Let C be a |V 1|×|V 2| integer table (Ci, j : the length of a longest string in subseq(P(v 1, i))∩subseq(P(v 2, j)) G 1 a 1 b 2 c 3 c 4 d 5 b 6 G 1 G 2 C a 1 c 2 d 3 d 4 b 5 b 6 a 1 b 2 c 3 G 2 a 1 c 2 d 3 d 4 b 5 b 6 c 4 d 5 b 6

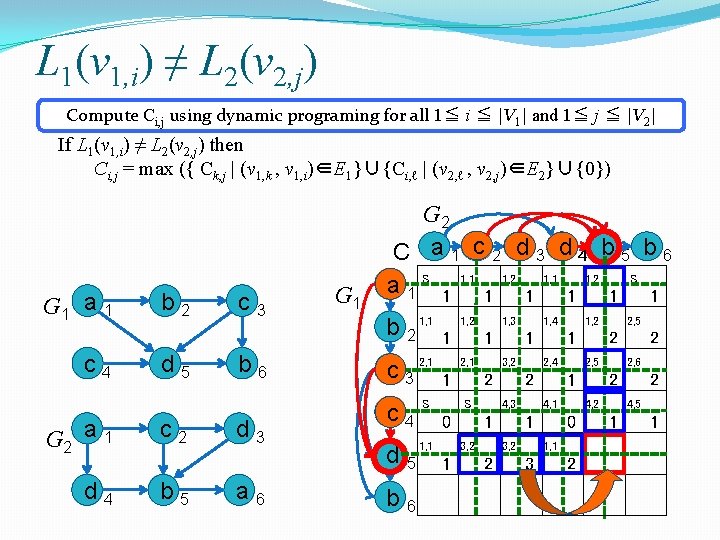
L 1(v 1, i) ≠ L 2(v 2, j) Compute Ci, j using dynamic programing for all 1≦ i ≦ |V 1| and 1≦ j ≦ |V 2| If L 1(v 1, i) ≠ L 2(v 2, j) then Ci, j = max ({ Ck, j | (v 1, k , v 1, i)∈E 1}∪{Ci, ℓ | (v 2, ℓ , v 2, j)∈E 2}∪{0}) G 1 a 1 c 4 b 2 d 5 c 3 b 6 G 1 G 2 C a 1 c 2 d 3 d 4 b 5 b 6 a 1 　S 1　 1, 1 1　 1, 2 1　 S 1　 b 2 1, 1 　 c 3 2, 1 　 S G 2 a 1 c 2 d 4 b 5 d 3 a 6 c 4　 1, 1 d 5　 b 6　 1, 2 　 1, 3 　 1, 4 　 1, 2 　 2, 5 　 1 2, 1 1 1 4, 3 1 3, 2 2 2 4, 1 　 4, 2 　 4, 5 　 0 　 1 　 0 3, 2 2 3, 2 　 2, 4 　 2, 5 　 2, 6 　 1 　 2 S 2 1, 1 1 1 5, 3 　　 1 　 2 　 3 　

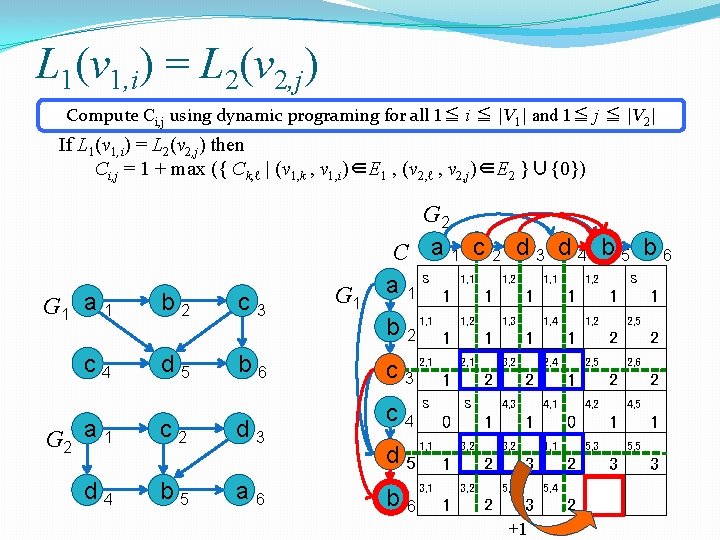
L 1(v 1, i) = L 2(v 2, j) Compute Ci, j using dynamic programing for all 1≦ i ≦ |V 1| and 1≦ j ≦ |V 2| If L 1(v 1, i) = L 2(v 2, j) then Ci, j = 1 + max ({ Ck, ℓ | (v 1, k , v 1, i)∈E 1 , (v 2, ℓ , v 2, j)∈E 2 }∪{0}) G 1 a 1 c 4 b 2 d 5 c 3 b 6 G 1 G 2 C a 1 c 2 d 3 d 4 b 5 b 6 a 1 　S 1　 1, 1 1　 1, 2 1　 S 1　 b 2 1, 1 　 c 3 2, 1 　 S G 2 a 1 c 2 d 4 b 5 d 3 a 6 c 4　 1, 1 d 5　 3, 1 b 6　 1, 2 　 1, 3 　 1, 4 　 1, 2 　 2, 5 　 1 2, 1 1 1 4, 3 1 2 3, 2 1, 1 1 5, 3 5, 4 1 5, 3 　 5, 5 　 1 　 2 　 3 3, 2 2 4, 1 　 4, 2 　 4, 5 　 0 　 1 　 0 3, 2 2 3, 2 　 2, 4 　 2, 5 　 2, 6 　 1 　 2 S 2 5, 3 1 　 2 　 3 　 2 　 4 　 +1 3 　

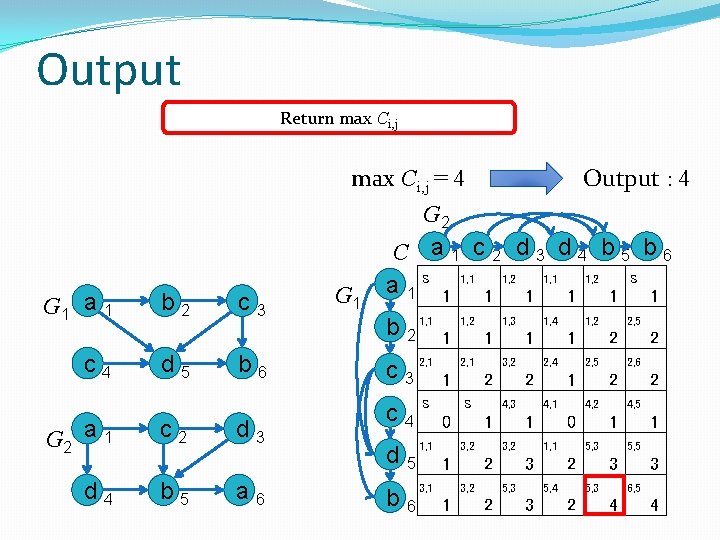
Output Return max Ci, j = 4 Output : 4 G 2 C a 1 c 2 d 3 d 4 b 5 b 6 G 1 a 1 c 4 b 2 d 5 c 3 b 6 G 1 a 1 　S b 2 1, 1 　 c 3 2, 1 　 S G 2 a 1 c 2 d 4 b 5 d 3 a 6 c 4　 1, 1 d 5　 3, 1 b 6　　 1, 1 　 1, 2 　 1 1 1 S 　 1 1, 2 　 1, 3 　 1, 4 　 1, 2 　 2, 5 　 1 2, 1 1 1 4, 3 1 2 3, 2 1, 1 1 5, 3 5, 4 1 5, 3 　 5, 5 　 1 　 2 　 3 3, 2 2 4, 1 　 4, 2 　 4, 5 　 0 　 1 　 0 3, 2 2 3, 2 　 2, 4 　 2, 5 　 2, 6 　 1 　 2 S 2 5, 3 3 6, 5 　 1 　 2 　 3 　 2 　 4

Time Complexity Sort vertices of G 1 and G 2 in topological order Linear time Let C be a |V 1|×|V 2| integer table (Ci, j : the length of a longest string in subseq(P(v 1, i))∩subseq(P(v 2, j)) Compute Ci, j using dynamic programing for all 1≦ i ≦ |V 1| and 1≦ j ≦ |V 2| Return max Ci, j O(|E 1||E 2|) time

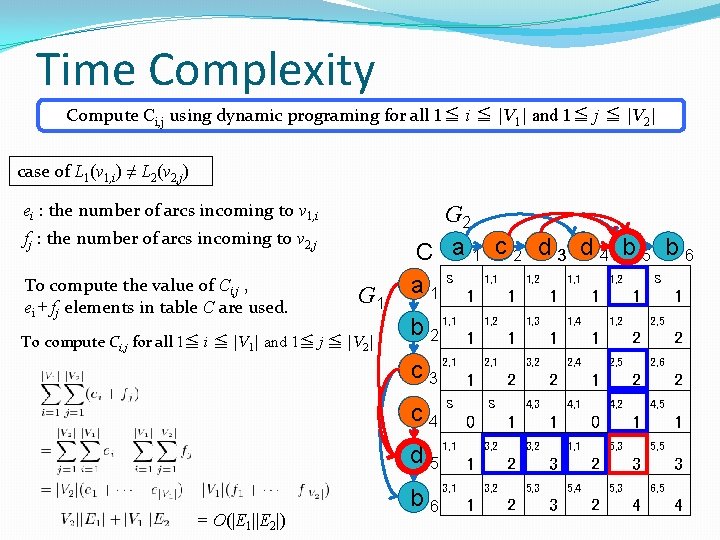
Time Complexity Compute Ci, j using dynamic programing for all 1≦ i ≦ |V 1| and 1≦ j ≦ |V 2| case of L 1(v 1, i) ≠ L 2(v 2, j) ei : the number of arcs incoming to v 1, i fj : the number of arcs incoming to v 2, j To compute the value of Ci, j , ei + fj elements in table C are used. G 1 To compute Ci, j for all 1≦ i ≦ |V 1| and 1≦ j ≦ |V 2| G 2 C a 1 c 2 d 3 d 4 b 5 b 6 a 1 　S 1　 1, 1 1　 1, 2 1　 S 1　 b 2 1, 1 　 c 3 2, 1 　 S c 4　 1, 1 d 5　 3, 1 = O(|E 1||E 2|) b 6　 1, 2 　 1, 3 　 1, 4 　 1, 2 　 2, 5 　 1 2, 1 1 1 4, 3 1 2 3, 2 1, 1 1 5, 3 5, 4 1 5, 3 　 5, 5 　 1 　 2 　 3 3, 2 2 4, 1 　 4, 2 　 4, 5 　 0 　 1 　 0 3, 2 2 3, 2 　 2, 4 　 2, 5 　 2, 6 　 1 　 2 S 2 5, 3 3 6, 5 　 1 　 2 　 3 　 2 　 4

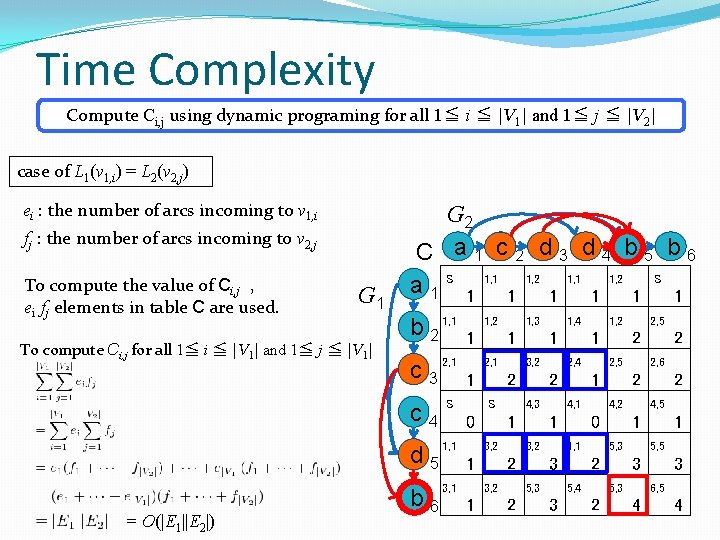
Time Complexity Compute Ci, j using dynamic programing for all 1≦ i ≦ |V 1| and 1≦ j ≦ |V 2| case of L 1(v 1, i) = L 2(v 2, j) ei : the number of arcs incoming to v 1, i fj : the number of arcs incoming to v 2, j To compute the value of Ci, j , ei fj elements in table C are used. G 1 To compute Ci, j for all 1≦ i ≦ |V 1| and 1≦ j ≦ |V 1| G 2 C a 1 c 2 d 3 d 4 b 5 b 6 a 1 　S 1　 1, 1 1　 1, 2 1　 S 1　 b 2 1, 1 　 c 3 2, 1 　 S c 4　 1, 1 d 5　 3, 1 = O(|E 1||E 2|) b 6　 1, 2 　 1, 3 　 1, 4 　 1, 2 　 2, 5 　 1 2, 1 1 1 4, 3 1 2 3, 2 1, 1 1 5, 3 5, 4 1 5, 3 　 5, 5 　 1 　 2 　 3 3, 2 2 4, 1 　 4, 2 　 4, 5 　 0 　 1 　 0 3, 2 2 3, 2 　 2, 4 　 2, 5 　 2, 6 　 1 　 2 S 2 5, 3 3 6, 5 　 1 　 2 　 3 　 2 　 4

Time Complexity Sort vertices of G 1 and G 2 in topological order Linear time Let C be a |V 1|×|V 2| interger array (Ci, j : the length of a longest string in subseq(P(v 1, i))∩subseq(P(v 2, j)) Compute Ci, j using dymnamic programing for all 1≦ i ≦ |V 1| and 1≦ j ≦ |V 2| O(|E 1||E 2|) time Return max Ci, j O(|V 1||V 2|) time The total time complexity is O(|E 1||E 2|) time.

Outline �Non-linear Text �Computing Longest Common Subsequence of Acyclic Non-linear Texts �Computing Longest Common Subsequence of Cyclic Non-linear Texts �Conclusions and Future works

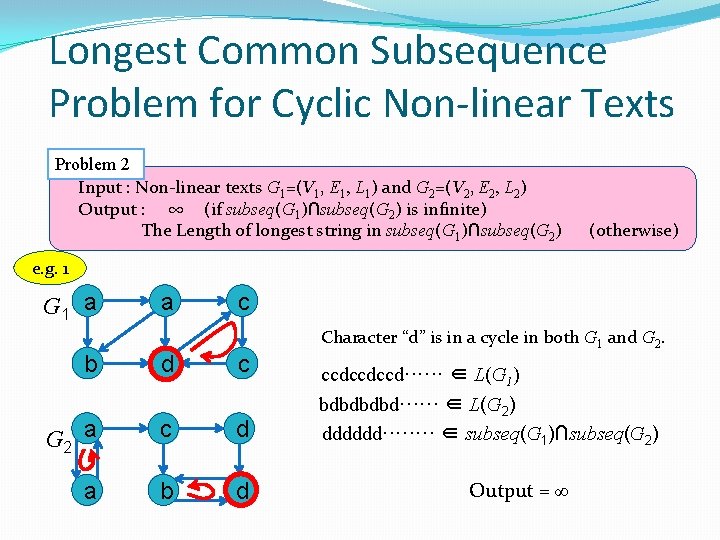
Longest Common Subsequence　 Problem for Cyclic Non-linear Texts Problem 2 　Input : Non-linear texts G 1=(V 1, E 1, L 1) and G 2=(V 2, E 2, L 2) 　Output : 　∞ (if subseq(G 1)∩subseq(G 2) is infinite) The Length of longest string in subseq(G 1)∩subseq(G 2) (otherwise) e. g. 1 G 1 a a c b d c G 2 a c d a b d Character “d” is in a cycle in both G 1 and G 2. ccdccdccd······ ∈ L(G 1) bdbd······ ∈ L(G 2) dddddd···· ∈ subseq(G 1)∩subseq(G 2) Output = ∞

Longest Common Subsequence　 Problem for Cyclic Non-linear Texts Problem 2 　Input : Non-linear texts G 1=(V 1, E 1, L 1) and G 2=(V 2, E 2, L 2) 　Output : 　∞ (if subseq(G 1)∩subseq(G 2) is infinite) The Length of longest string in subseq(G 1)∩subseq(G 2) (otherwise) e. g. 2 G 1 a a c b d c G 2 a c d a b a subseq(G 1)∩subseq(G 2) = {a, b, c, d, aa, ab, ac, ad, cd, aab, aac, aad, acd, aacd} Output = 4

Algorithm 2 : Computing the length of longest common subsequence of cyclic non-linear texts Transform G 1 and G 2 into G’ 1 and G’ 2 based on the strongly connected components Check whether subseq(G 1)∩subseq(G 2) is infinite or not Sort vertices of G’ 1 and G’ 2 in topological order Let C be a |V’ 1|×|V’ 2| integer table (Ci, j : the length of a longest string in subseq(P(v’ 1, i))∩subseq(P(v’ 2, j)) Compute Ci, j using dynamic programing for all 1≦ i ≦ |V’ 1| and 1≦ j ≦ |V’ 2| Return max Ci, j

Strongly Connected Component Transform G 1 and G 2 into G’ 1 and G’ 2 based on the strongly connected components G 1 a a c G’ 1{a} 1 b d c {b} 3 {a} 2 {c, d} 4 transform G 2 a c d a b a G’ 2 {a} 1 {c} 2 {d} 3 {a, b} 4 strongly connected component cyclic non-linear texts acyclic non-linear texts

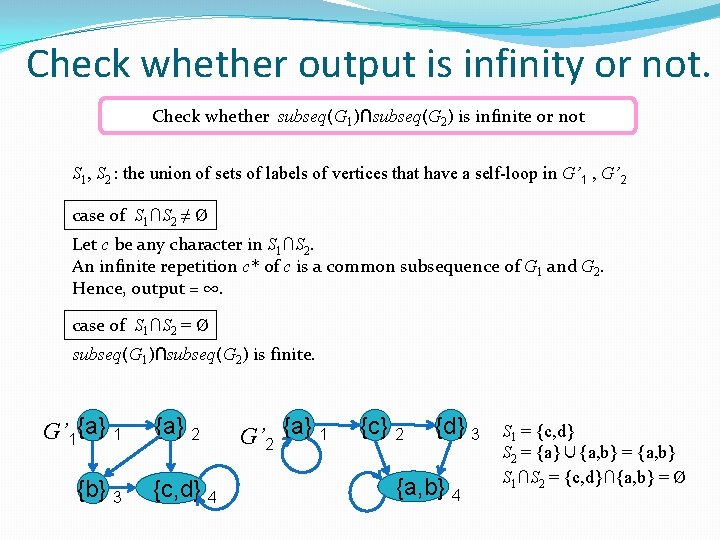
Check whether output is infinity or not. Check whether subseq(G 1)∩subseq(G 2) is infinite or not S 1, S 2 : the union of sets of labels of vertices that have a self-loop in G’ 1 , G’ 2 case of S 1∩S 2 ≠ Ø Let c be any character in S 1∩S 2. An infinite repetition c* of c is a common subsequence of G 1 and G 2. Hence, output = ∞. case of S 1∩S 2 = Ø subseq(G 1)∩subseq(G 2) is finite. G’ 1{a} 1 {b} 3 {a} 2 {c, d} 4 G’ 2 {a} 1 {c} 2 {d} 3 {a, b} 4 S 1 = {c, d} S 2 = {a}∪{a, b} = {a, b} S 1∩S 2 = {c, d}∩{a, b} = Ø

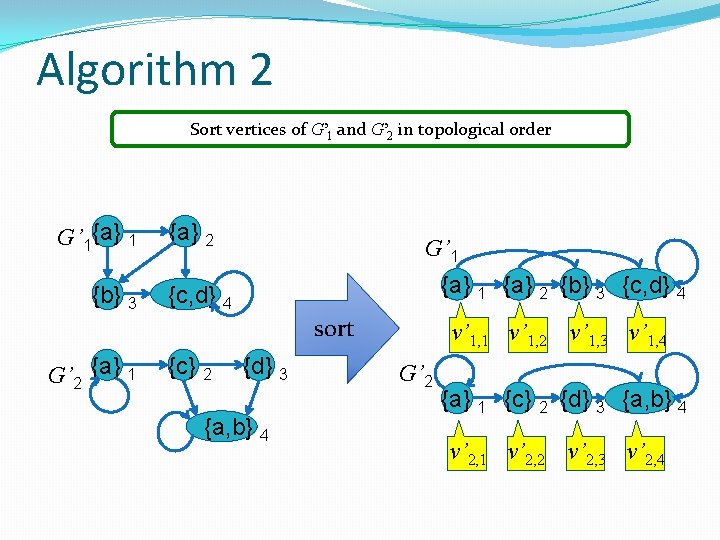
Algorithm 2 Sort vertices of G’ 1 and G’ 2 in topological order G’ 1{a} 1 {b} 3 {a} 2 G’ 1 {a} 2 {b} 3 {c, d} 4 sort G’ 2 {a} 1 {c} 2 {d} 3 {a, b} 4 v’ 1, 1 v’ 1, 2 v’ 1, 3 v’ 1, 4 G’ 2 {a} 1 {c} 2 {d} 3 {a, b} 4 v’ 2, 1 v’ 2, 2 v’ 2, 3 v’ 2, 4

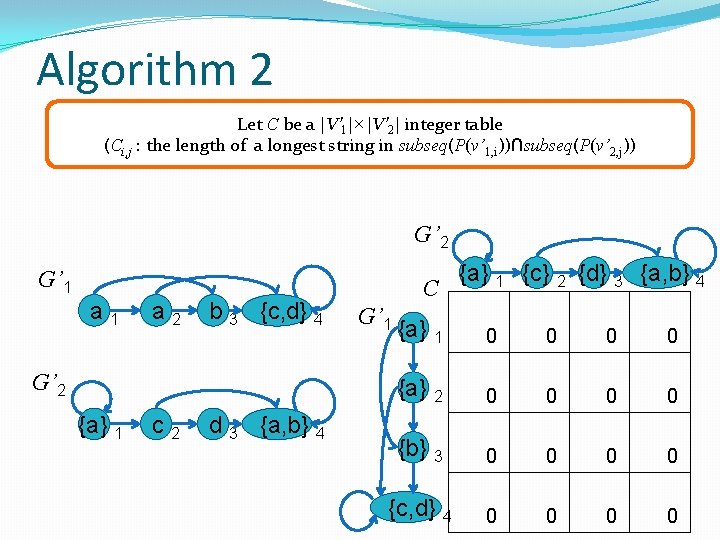
Algorithm 2 Let C be a |V’ 1|×|V’ 2| integer table (Ci, j : the length of a longest string in subseq(P(v’ 1, i))∩subseq(P(v’ 2, j)) G’ 2 G’ 1 a 2 b 3 {c, d} 4 G’ 2 {a} 1 c 2 d 3 {a, b} 4 C G’ 1 {a} 1 {c} 2 {d} 3 {a, b} 4 {a} 1 0 0 {a} 2 0 0 {b} 3 0 0 {c, d} 4 0 0

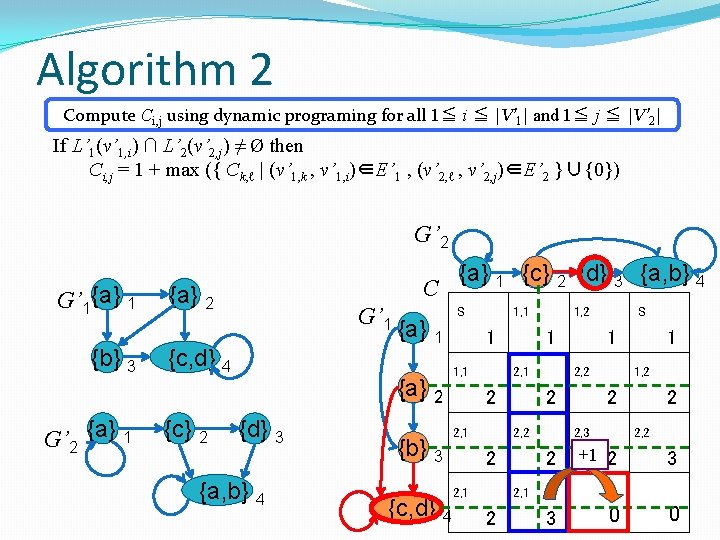
Algorithm 2 Compute Ci, j using dynamic programing for all 1≦ i ≦ |V’ 1| and 1≦ j ≦ |V’ 2| If L’ 1(v’ 1, i) ∩ L’ 2(v’ 2, j) ≠ Ø then Ci, j = 1 + max ({ Ck, ℓ | (v’ 1, k , v’ 1, i)∈E’ 1 , (v’ 2, ℓ , v’ 2, j)∈E’ 2 }∪{0}) G’ 2 G’ 1{a} 1 {b} 3 G’ 2 {a} 1 C {a} 2 G’ 1 {c, d} 4 {c} 2 {a} 1 {a} 2 {d} 3 {a, b} 4 {b} 3 {a} 1 {c} 2 {d} 3 {a, b} 4 S 　　 1 1, 1 　 2 2, 1 1, 1 　 1 2, 1 　　 2 2, 2 2 {c, d} 4 　 2 1, 2 　 2 2, 1 　　 S 1 2, 2 　　 1 1, 2 2 　 2 2, 3 　 +1 　 2 3 40 0 2, 2 　 4, 2 3 　

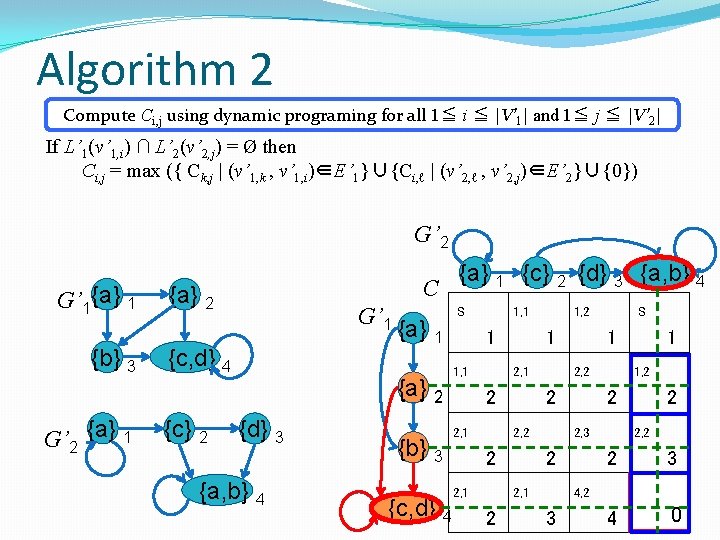
Algorithm 2 Compute Ci, j using dynamic programing for all 1≦ i ≦ |V’ 1| and 1≦ j ≦ |V’ 2| If L’ 1(v’ 1, i) ∩ L’ 2(v’ 2, j) = Ø then Ci, j = max ({ Ck, j | (v’ 1, k , v’ 1, i)∈E’ 1}∪{Ci, ℓ | (v’ 2, ℓ , v’ 2, j)∈E’ 2}∪{0}) G’ 2 G’ 1{a} 1 {b} 3 G’ 2 {a} 1 C {a} 2 G’ 1 {c, d} 4 {c} 2 {a} 1 {a} 2 {d} 3 {a, b} 4 {b} 3 {a} 1 {c} 2 {d} 3 {a, b} 4 S 　　 1 1, 1 　 2 2, 1 1, 1 　 1 2, 1 　　 2 2, 2 2 {c, d} 4 　 2 1, 2 　 2 2, 1 　　 1 2, 2 　 2, 3 　　 2 　 1, 2 　 2 2, 2 　 3 4, 3 4 　 1 2 4, 2 3 S 　　 40

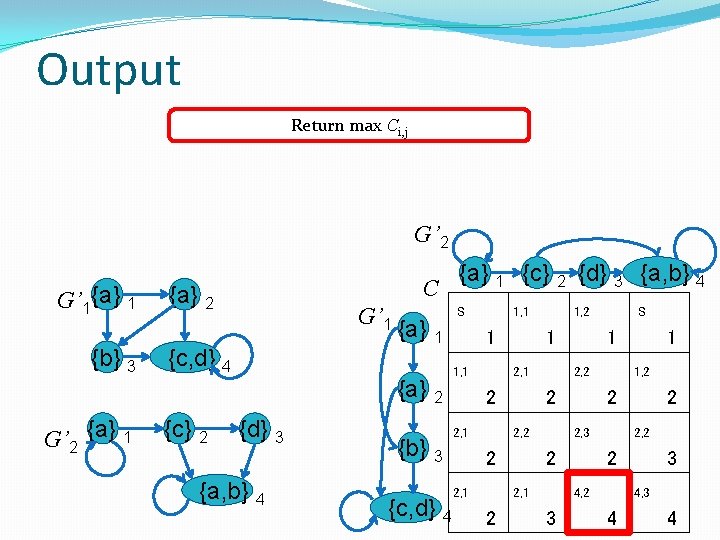
Output Return max Ci, j G’ 2 G’ 1{a} 1 {b} 3 G’ 2 {a} 1 C {a} 2 G’ 1 {c, d} 4 {c} 2 {a} 1 {a} 2 {d} 3 {a, b} 4 {b} 3 {a} 1 {c} 2 {d} 3 {a, b} 4 S 　　 1 1, 1 　 2 2, 1 1, 1 　 1 2, 1 　　 2 2, 2 2 {c, d} 4 　 2 1, 2 　 2 2, 1 　　 1 2, 2 　 2, 3 　　 2 　 4 　 1 1, 2 2 4, 2 3 S 　 2 2, 2 　 3 4, 3 　　 4

Time Complexity Transform G 1 and G 2 into G’ 1 and G’ 2 based on the strongly connected components Check whether subseq(G 1)∩subseq(G 2) is infinite or not Sort vertices of G’ 1 and G’ 2 in topological order Let C be a |V’ 1|×|V’ 2| integer table (Ci, j : the length of a longest string in subseq(P(v’ 1, i))∩subseq(P(v’ 2, j)) Linear time O(|Σ|log|Σ|) time Linear time Compute Ci, j using dynamic programing for all 1≦ i ≦ |V’ 1| and 1≦ j ≦ |V’ 2| O(|E’ 1||E’ 2|+|V’ 1||V’ 2|log|Σ|) time Return max Ci, j Compare L’(v 1, i) and L’(v 2, j)

Time Complexity Transform G 1 and G 2 into G’ 1 and G’ 2 based on the strongly connected components Check whether subseq(G 1)∩subseq(G 2) is infinite or not Sort vertices of G’ 1 and G’ 2 in topological order Linear time O(|Σ|log|Σ|) time Linear time The total complexity is O(|E 1||E 2|+|V 1||V 2|log|Σ|) time. Let C betime a |V’ 1|×|V’ 2| integer table (Ci, j : the length of a longest string in subseq(P(v’ 1, i))∩subseq(P(v’ 2, j)) Compute Ci, j using dynamic programing for all 1≦ i ≦ |V’ 1| and 1≦ j ≦ |V’ 2| Return max Ci, j O(|E’ 1||E’ 2|+|V’ 1||V’ 2|log|Σ|) time O(|V’ 1||V’ 2|) time

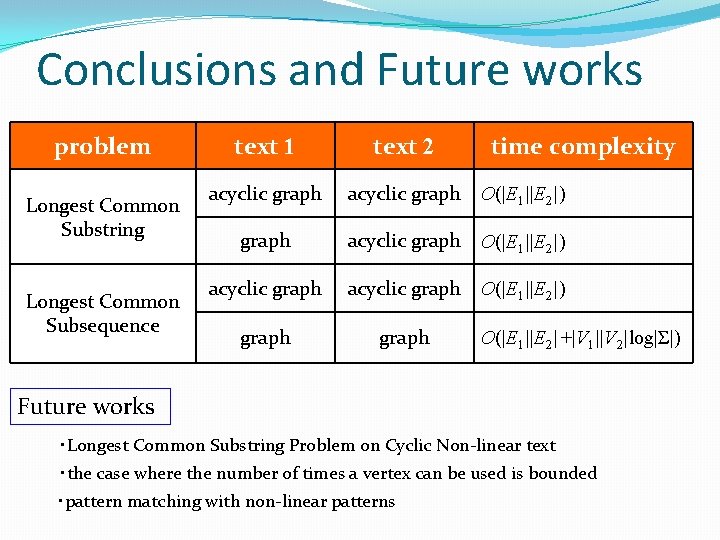
Conclusions and Future works problem Longest Common Substring Longest Common Subsequence text 1 text 2 time complexity acyclic graph O(|E 1||E 2|) graph acyclic graph O(|E 1||E 2|) graph O(|E 1||E 2|+|V 1||V 2|log|Σ|) Future works ・Longest Common Substring Problem on Cyclic Non-linear text ・the case where the number of times a vertex can be used is bounded ・pattern matching with non-linear patterns

Thank You For Listening