Linear Relationships coordinates nonlinear gradient magnitude linear equation

Linear Relationships coordinates non-linear gradient magnitude linear equation decreasing point pronumeral solution graph reflections relationship plot increasing Cartesian plane derive transformation parallel translations origin continuous rotations scale image intersecting pattern perpendicular table of values

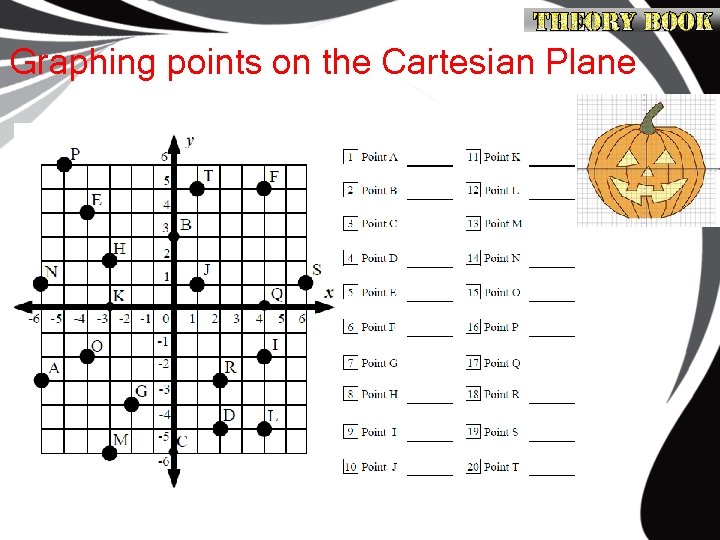
Vocabulary Activities Write the list words in ALPHABETICAL ORDER Which list word means: pronumeral A letter which represents a number _______ solution Another word for answer _____ Diminishing in value _______ decreasing graph A picture which shows information in mathematics ______ parallel Lines which never intersect are called _______ perpendicular Lines which meet at a right angle are called _______ plot The process which puts points onto a graph _______ origin Another name for the point (0, 0) _______ magnitude Another word for size _______

Graphing points on the Cartesian Plane

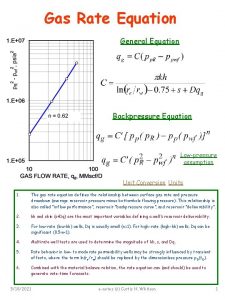
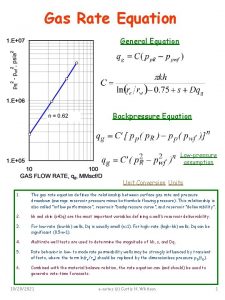
Number Patterns

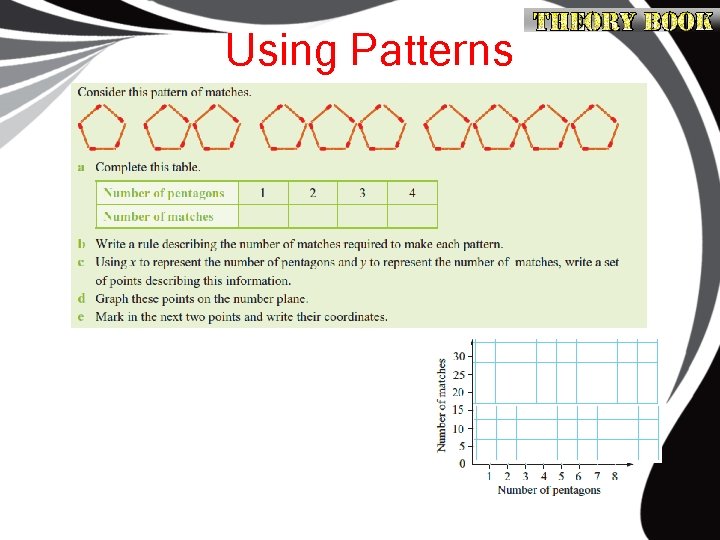
Using Patterns

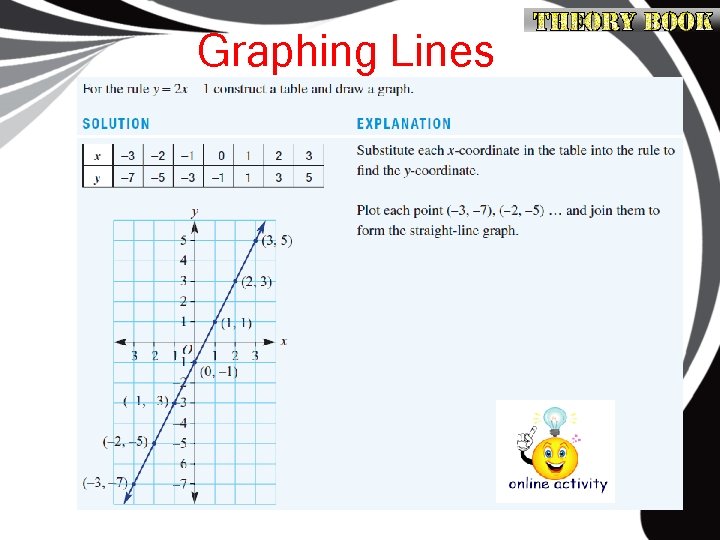
Graphing Lines

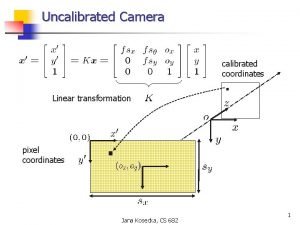
Finding the Equation of a Line A rule must be true for every pair of coordinates (x, y) in a table or graph. coefficient of x constant y= □×x+ □ □ □ Consider a linear rule of the form y = ×x+. The coefficient of x will be the increase in y as x increases by 1. If there is a decrease in y, then the coefficient will be negative.

Finding the Equation of a Line

Using Intercepts to Sketch a Line

Intersection of Lines Solve the equation 4 - x = 2 x + 1.

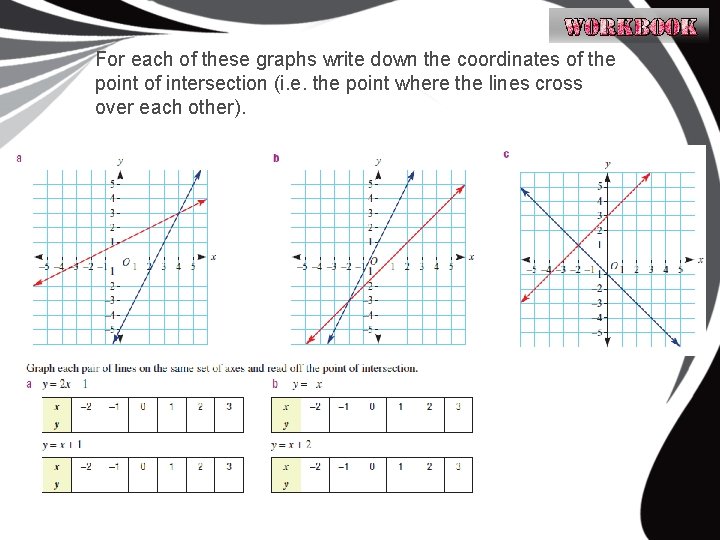
For each of these graphs write down the coordinates of the point of intersection (i. e. the point where the lines cross over each other).

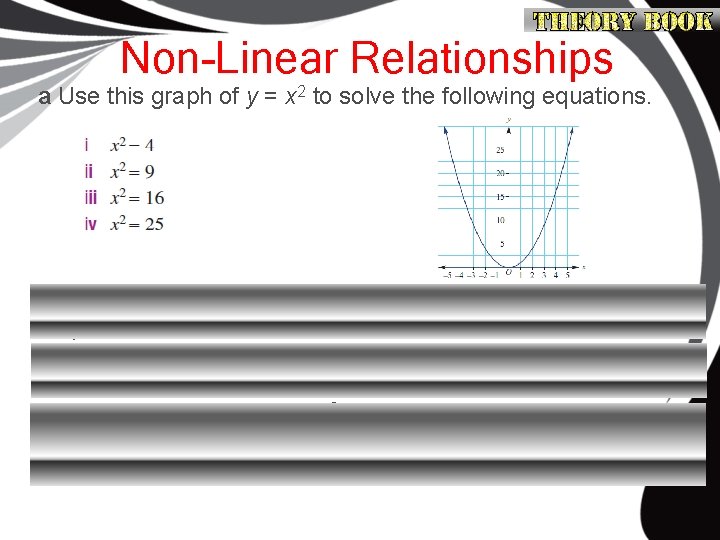
Non-Linear Relationships a Use this graph of y = x 2 to solve the following equations. b Explain why there are two solutions to each of the equations in question a above. c Give one reason why the graph of y = x 2 does not give a solution to the equation x 2 = -9. d Graph y = x + 2 and y = x 2 on the same screen and graphically solve x 2 = x + 2 by finding the x values of the points of intersection.