Fyzika 6 ronk Z Fyzikln veliina Hmotnost Creation

Fyzika 6. ročník ZŠ Fyzikální veličina Hmotnost Creation IP&RK Page 1

Popis fyzikální veličiny K určení množství látky v tělese používáme fyzikální veličinu HMOTNOST. Hmotnost tělesa určujeme VÁŽENÍM. Značka : m [„mass“ doslovný překlad z AJ je hmota] Jednotka: kilogram (1 kg ) KILOGRAM je roven hmotnosti mezinárodního prototypu kilogramu uloženého u Mezinárodního úřadu pro míry a váhy v Sèvres (Francie). Někdy na konci 18. století byl stanoven 1 kg jako hmotnost 1 dm 3 odstáté vody o teplotě 4 °C. Dnes váleček s průměrem a výškou 39 mm . Definice a její problémy Page 2

Jak se projevuje hmotnost tělesa? • Gravitačním přitahováním – Čím je větší hmotnost tělesa, tím větší gravitační silou je přitahováno k Zemi • Druhým projevem je schopnost tělesa bránit se změnám pohybu – Roztlačíme snadněji prázdný nákupní vozík než vozík plně naložený Page 3

Jednotky hmotnosti Základní jednotka: kilogram - značka - kg Odvozené jednotky: tuna - značka - t metrický cent - značka - q dekagram - značka - dag gram - značka - g centigram - značka - cg miligram - značka - mg . 100 metrický cent tuna : 100 . 10 kilogram dekagram : 100 : 10 . 100 gram . 10 centigram : 100 : 10 Page 4

Historické jednotky hmotnosti Metrický cent 1 q = 100 kg Unce 1 oz = 28, 4 g Grain (zrno) 1 gr = 65 mg Karát 1 Kt = 0, 2 g Libra 1 lb = 0, 45 kg Trojská unce = 31, 1 g a další Staré české i cizí jednotky – zajímavosti najdete T A D Y nebo T U Něco více z historie měření hmotnosti najdete na jiné webové stránce Z D E Page 5

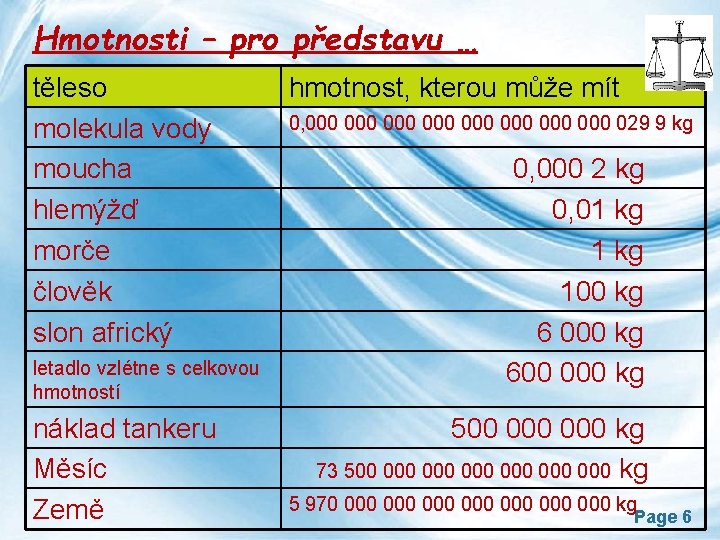
Hmotnosti – pro představu … těleso molekula vody moucha hlemýžď morče člověk slon africký letadlo vzlétne s celkovou hmotností náklad tankeru Měsíc Země hmotnost, kterou může mít 0, 000 000 029 9 kg 0, 000 2 kg 0, 01 kg 100 kg 6 000 kg 600 000 kg 500 000 kg 73 500 000 000 000 kg 5 970 000 000 kg Page 6

Vážení • K měření hmotnosti tělesa využijeme gravitační přitahování • Takovému měření hmotnosti říkáme VÁŽENÍ Rovnoramenné váhy Tělesa stejné hmotnosti Tělesa různé hmotnosti Page 7

Vážení na rovnoramenné váze Na jednu z misek přidáváme závaží se známou hmotností až do okamžiku, kdy jazýček vah ukazuje na nulu. Sečteme hmotnost všech závaží na misce. Součet všech závaží je i hmotností měřeného tělesa. Na rovnoramenných vahách měříme hmotnost tím, že porovnáváme hmotnost tělesa s hmotností závaží, kterou známe. Page 8

Rovnoramenné váhy - popis Page 9

Závaží, jaká se používají u laboratorních vah Page 10

Váhy využívající změny tvaru pružných těles Osobní pružinová váha Mincíř Závěsná pružinová váha Tyto váhy jsou vlastně siloměry. Page 11

Digitální váhy • Princip – elektronicky zpracují protažení nebo ohnutí pružného tělesa Obchodní váhy, Digitální laboratorní váhy kromě hmotnosti ukazují i cenu Váhy nerovnoramenné Založené na vlastnostech páky PŘEZMEN využívá se při vážení ryb Page 12

Zajímavosti • Stejné těleso by bylo na povrchu různých planet přitahováno různou silou. • Osobní váha, která na Zemi ukazuje 50 kg, by na Měsíci ukázala jen 8, 3 kg (6 x méně), na Jupiteru ale 126 kg!!! • Na kosmické stanici ve stavu beztíže by ukázala nulu. Které váhy by vážily dobře i na Měsíci? Rovnoramenné (neměnil by se poměr váženého tělesa a závaží). Pružinové by ukazovaly asi 6 x méně. Page 13

Otázky 1. Jak se nazývá základní jednotka hmotnosti? 2. Uveď příklad tělesa ze svého okolí, které má hmotnost 1 kg. 3. Jaké znáš vedlejší jednotky hmotnosti? 4. S čím porovnáváme hmotnost tělesa na rovnoramenných vahách? 5. Vysvětli, co děláme, když aretujeme váhy. Kdy provádíme aretaci a proč? 6. Popiš, jak postupuješ při měření hmotnosti pevného tělesa na rovnoramenných vahách. 7. Co musíš udělat navíc při měření hmotnosti kapaliny na rovnoramenných vahách? Page 14

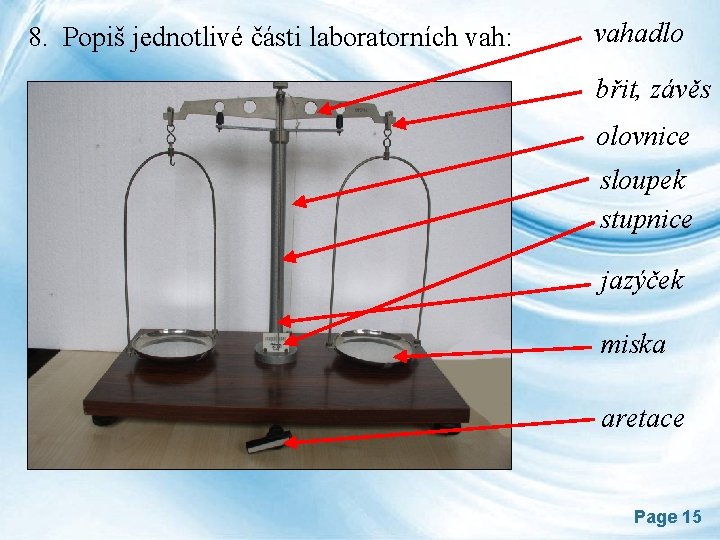
8. Popiš jednotlivé části laboratorních vah: vahadlo břit, závěs olovnice sloupek stupnice jazýček miska aretace Page 15

Zapiš a zapamatuj • Hmotnost těles se měří s využitím gravitační síly. • Tomuto měření říkáme vážení a měřicí zařízení jsou váhy. • Váhy mohou využívat závaží, příkladem jsou váhy rovnoramenné. • Praktičtější váhy jsou založené na protažení nebo ohýbání pružných těles. Page 16

Dvakrát měř, a nedávej si závaží na nohu !!! Page 17