Functions Mappings Definitions A function or mapping from




















- Slides: 23

Functions (Mappings)

Definitions • A function (or mapping) from a set A to a set B is a rule that assigns to each element a of A exactly one element b of B. • The set A is called the domain of , and B is called the range of . • If assigns b to a, then b is called the image of a under . • The subset of B comprising all the images of elements of A is called the image of A under

Notation • A –> B means is a mapping from set A to set B. • (a) = b or : a –> b means that function maps element a to element b (i. e. the image of a is b).

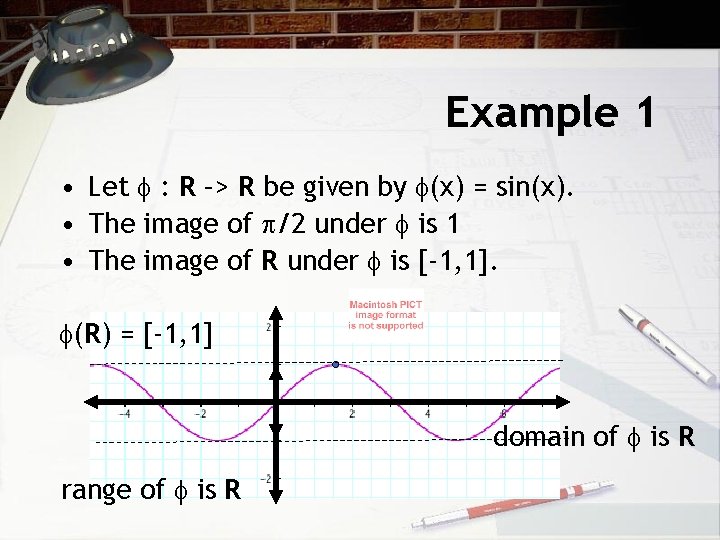
Example 1 • Let : R –> R be given by (x) = sin(x). • The image of /2 under is 1 • The image of R under is [-1, 1]. (R) = [-1, 1] domain of is R range of is R

Example 2 • : Q –> Z given by : p/q –> p+q • (1/2) = 1 + 2 = 3 (2/4) = 2 + 4 = 6 Since 1/2 = 2/4, but (1/2) ≠ (2/4) is not a function!

To prove a rule is a function • Assume x 1 = x 2 • Show (x 1) = (x 2) • In this case we say that is well-defined.

Show is well-defined • Let : Z –> Z be given by (n) = n 2 mod 2 • Suppose n 1 = n 2. • (n 1)– (n 2) = n 12 mod 2 –n 22 mod 2 = (n 1 – n 2)(n 1+n 2) mod 2 =0 since (n 1 – n 2) = 0 • So (n 1) = (n 2) • Therefore, is well-defined.

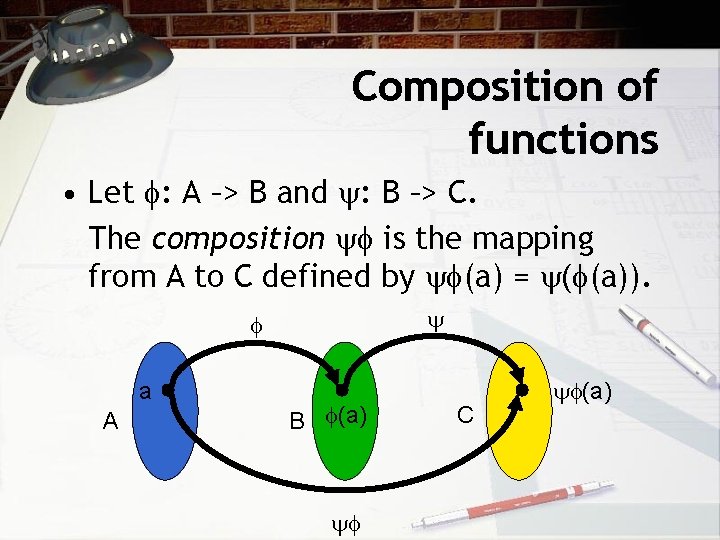
Composition of functions • Let : A –> B and : B –> C. The composition is the mapping from A to C defined by (a) = ( (a)). a A B (a) C (a)

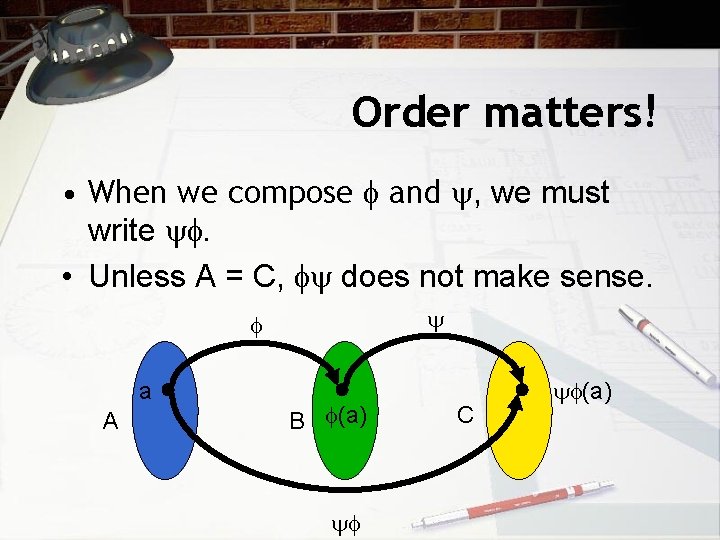
Order matters! • When we compose and , we must write • Unless A = C, does not make sense. a A B (a) C (a)

One to one functions • A function from a set A is called one-to -one if • Note: This is the converse to the welldefined condition.

Show not one-to-one • Show : R –> R given by (x) = x 2 is not one–to–one. • (– 2)= 4 = (2), but – 2 ≠ 2 • So is not one-to-one.

Show one-to-one • Show : [0, ∞) –> R given by (x) = x 2 is one–to– one. • Suppose (x 1)= (x 2). • Then 0 = (x 1)– (x 2) = x 12–x 22 = (x 1–x 2)(x 1+x 2) • So either (x 1–x 2) = 0 or (x 1+x 2) = 0 • If (x 1–x 2) = 0, then x 1= x 2 • If (x 1+x 2) = 0, then x 1= x 2 = 0 since the domain is [0, ∞) • In either case, x 1 = x 2, so is one-to-one.

Onto functions • A function from a set A to a set B is said to be onto B if each element of B is the image of at least one element of A.

Show not onto • Show : [0, ∞) –> R given by (x) = x 2 is not onto. • Suppose – 1 = (x) for some x in [0, ∞). • Then -1 = x 2 ≥ 0 • This counterexample shows is not onto.

Show onto • Show : [0, ∞) –> [0, ∞) given by (x) = x 2 is onto. • Proof: Choose any number b ≥ 0. • Let a = √b. • Then (a) = (√b)2 = b. • So is onto.

Properties of functions • Given : A–>B, : B–>C, and : C–>D, then 1. ( ) = ( ). (Associativity) 2. If and are one-to-one, then is one-to-one. 1. If and are onto, then is onto. • If is one-to-one and onto, then there is a function -1 from B to A such that -1 (a)=a for all a in A and -1(b)=b for all b in B.

Proof of Associativity • • • Choose any a in A. Let b = (a), c = (b), and d = (c). Notice that (a) = c and (b) = d. Then ( ) (a) = (b) = d Also, ( )(a) = (c) = d Since ( ) (a) = ( )(a) for all a in A, ( ) = ( )

Prove one-to-one • Suppose (x 1) = (x 2) • Set y 1 = (x 1) and y 2 = (x 2). Then (y 1) = (y 2) • Since is one-to-one, y 1=y 2 But then (x 1) = (x 2). • Since is one-to-one, x 1 = x 2. • Therefore, is one-to-one.

Prove onto • Choose any c in C • Since is onto, there is a b in B with (b)=c. • Since is onto, there is an a in A with (a)=b. • Then (a) = (b) = c • Therefore, is onto.

Proof of inverse functions • The proof consists of three steps. 1. Construct the inverse function. 2. Show that the inverse is well-defined. 3. Show that the inverse function has the required cancellation properties.

1. Construction • Given : A->B is one-to-one and onto. • Choose any b in B. Since is onto, there is an a in A with (a)=b. Set -1(b) = a.

2. Well-defined • • Suppose b 1 = b 2 in B. Let a 1 = -1(b 1) and a 2 = -1(b 2) Then (a 1) = b 1 = b 2 = (a 2) Since is one-to-one, a 1 = a 2 That is, -1(b 1) = -1(b 2) • Therefore, -1 is well-defined.

3. Cancellation • Choose any a in A. • Set b = f(a) and note that -1(b) = a. • Then -1 (a) = -1 (b) = a, and -1(b) = (a) = b. • Since -1 is well-defined and the cancellation laws hold, we are done.
 Hematyria
Hematyria Memory parameters
Memory parameters Forward mapping vs backward mapping
Forward mapping vs backward mapping Terjemahan
Terjemahan Mapping by elementary functions
Mapping by elementary functions Mapping function definition
Mapping function definition Piecewise function absolute value
Piecewise function absolute value Evaluating functions and operations on functions
Evaluating functions and operations on functions Evaluating functions and operations on functions
Evaluating functions and operations on functions Definition of nursing as a profession
Definition of nursing as a profession What are the three types of irony and their definitions
What are the three types of irony and their definitions The problem of concept drift: definitions and related work
The problem of concept drift: definitions and related work Striker welding definition
Striker welding definition Cheek cut rafter
Cheek cut rafter Range of motion definitions
Range of motion definitions Speech to actuate definition
Speech to actuate definition Education psychology meaning
Education psychology meaning Rag status reporting
Rag status reporting Poverty definition
Poverty definition Meaning of non verbal communication
Meaning of non verbal communication Microteaching phases
Microteaching phases Revision materials
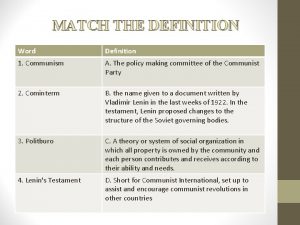
Revision materials Match the following terms with their definitions communism
Match the following terms with their definitions communism Defining leadership
Defining leadership