Functional linear models Three types of linear model

Functional linear models

Three types of linear model to consider: 1. 2. 3. Response is a function; covariates are multivariate. Response is scalar or multivariate; covariates are functional. Both response and covariates are functional.

Functional response with multivariate covariates n n n Response: Covariate: Model: yi(t), i=1, …, N xi 1, …, xip

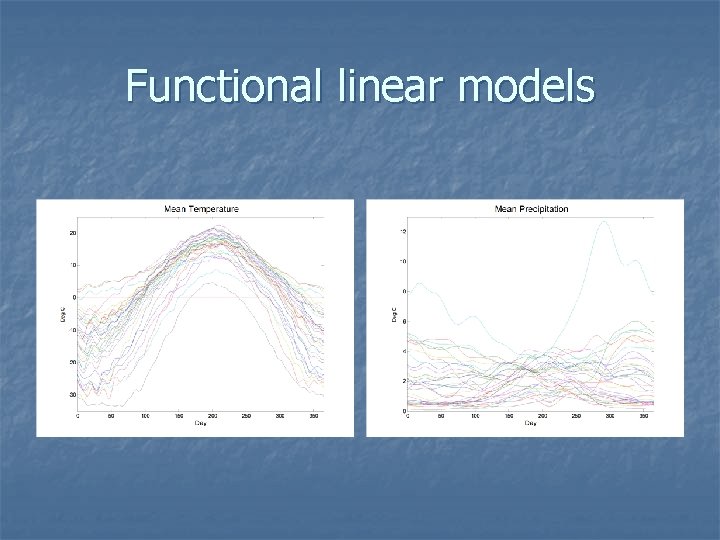
How does daily temperature depend on climate zone? n n n 35 Canadian temperature stations, divided into four zones: Atlantic, Pacific, Continental, and Arctic. Response is 30 -year average daily temperature. A functional one-way analysis of variance, set up to have a main effect, and zone effects summing to zero.

Analyzing the data n n n This is straightforward. If Y(t) is the N-vector of response functions, β(t) is the 5 -vector of regression functions (main effect + zone effects), then the LS estimate is β(t) = (X’X)-1 X’ Y(t).

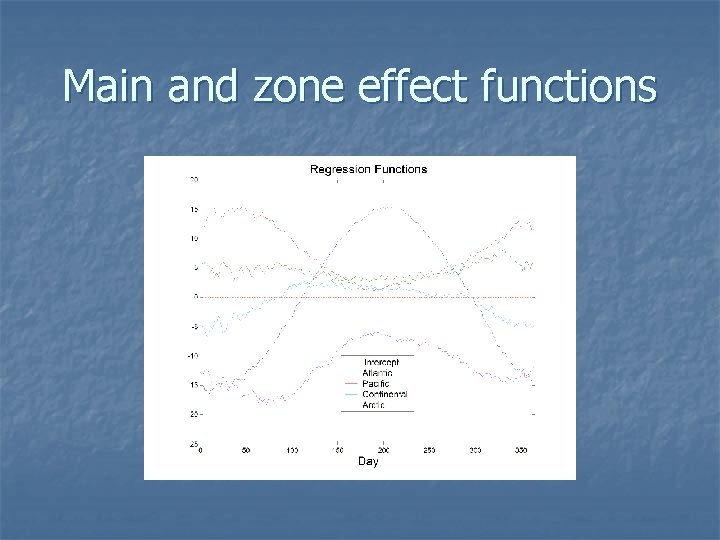
Main and zone effect functions

Assessing effects n n n We probably want to assess effects pointwise: For what times t is an effect substantial? This can be done using F-ratios conditional on t, pointwise confidence bands, etc. The multiple comparison problem is especially challenging here.

Response is scalar, Covariate is a single functional variable n n n Response: yi , i=1, …, N Covariate: xi (t) Model:

We have to smooth! n n n The technical and conceptual issues become much more interesting when the covariate is functional. A functional covariate is effectively an infinitedimensional predictor for a finite set of N responses. We can fit the data exactly! Smoothing becomes essential; without it, β(t) will be unacceptably rough, and we won’t learn anything useful.

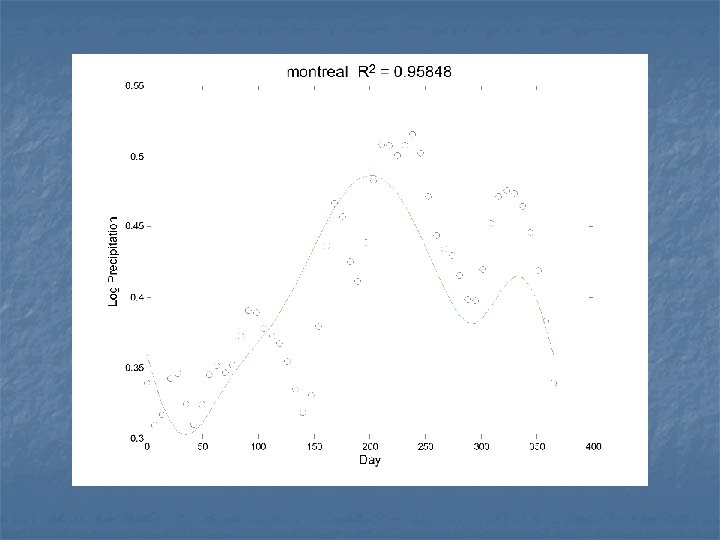
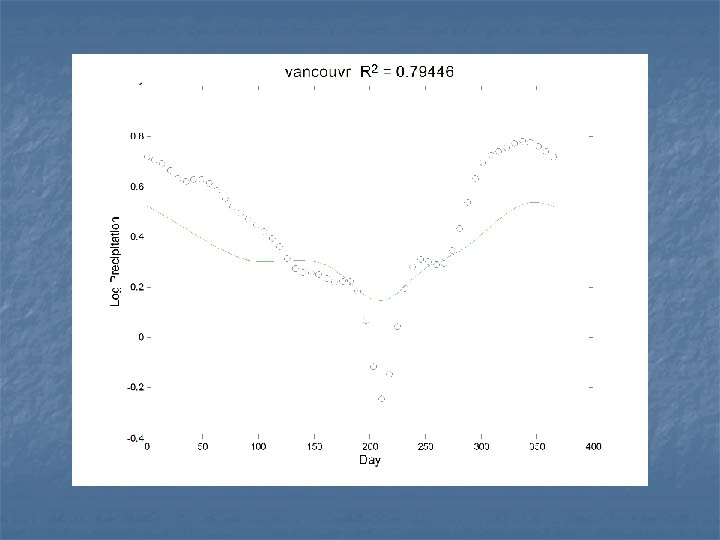
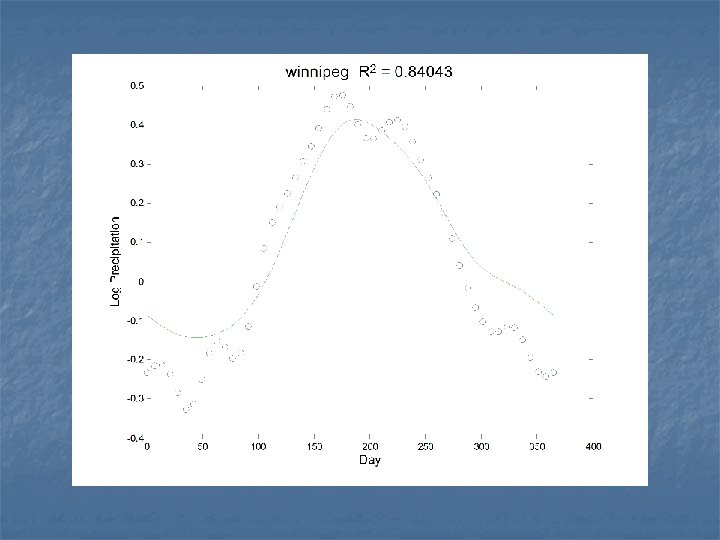
Predicting log annual precipitation from the temperature profiles n n n Can we determine how much precipitation a weather station will receive from the shape of the temperature profile? What roughness penalty should we use to smooth β(t) ? We penalize the size of (2π/365)2 Dβ+D 3β, the harmonic acceleration of β(t). This smooths towards a shifted sinusoid.

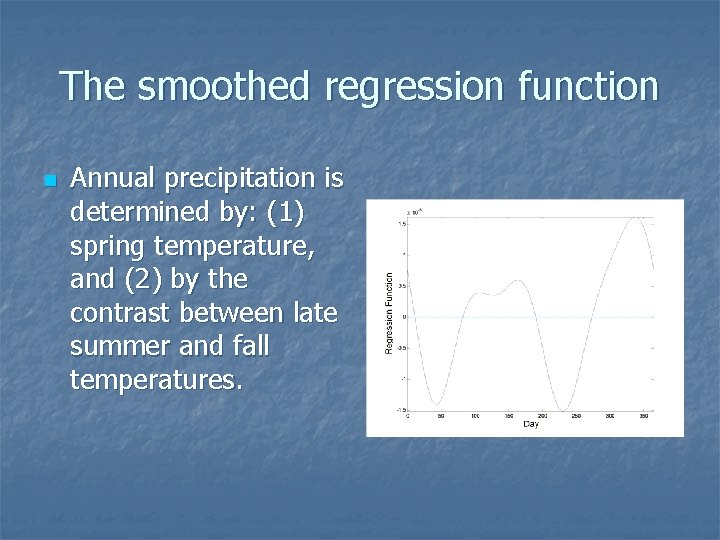
The smoothed regression function n Annual precipitation is determined by: (1) spring temperature, and (2) by the contrast between late summer and fall temperatures.

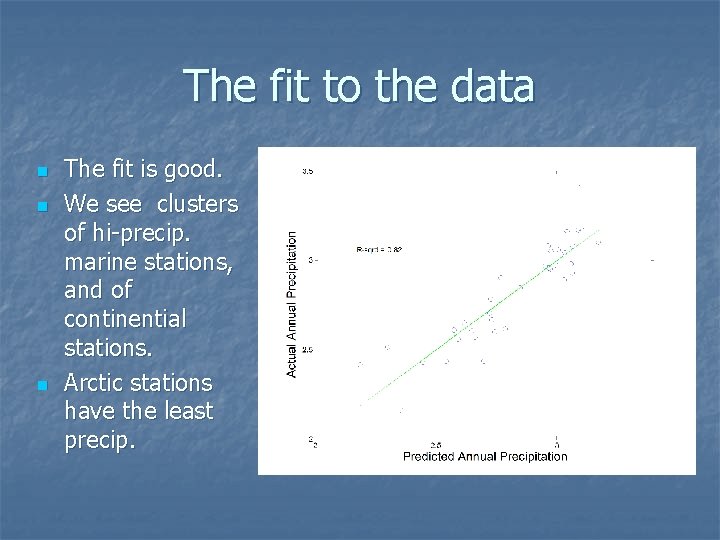
The fit to the data n n n The fit is good. We see clusters of hi-precip. marine stations, and of continential stations. Arctic stations have the least precip.

What about both the response and covariate being functional? Response y(t), covariate x(s) or x(s, t). Here we have a lot of possibilities. We can predict y(t) using the shape of x(s, t) over: n all of s, especially for periodic data, n only at s = t, concurrent influence only, or for some delay s = t – δ, n s t, no feed forward, n some region Ωt depending on t. n

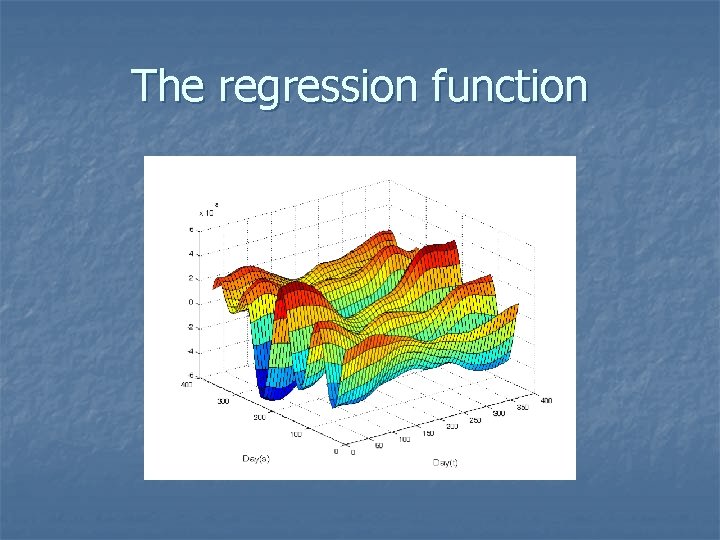
Predicting the precipitation profile from the temperature profile n The model is: In this case we have to smooth β(s, t) with respect to both s and t.

The regression function

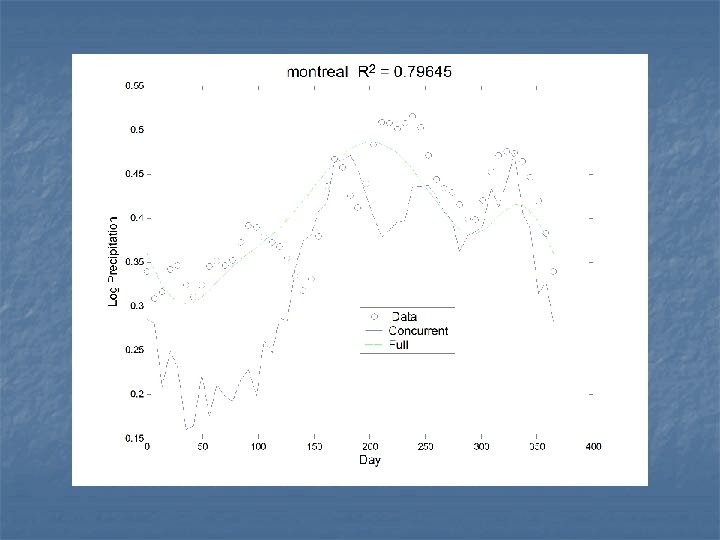
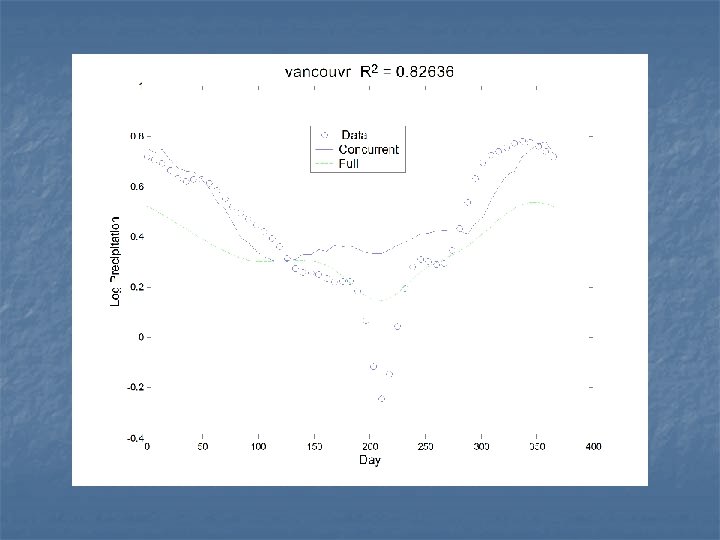
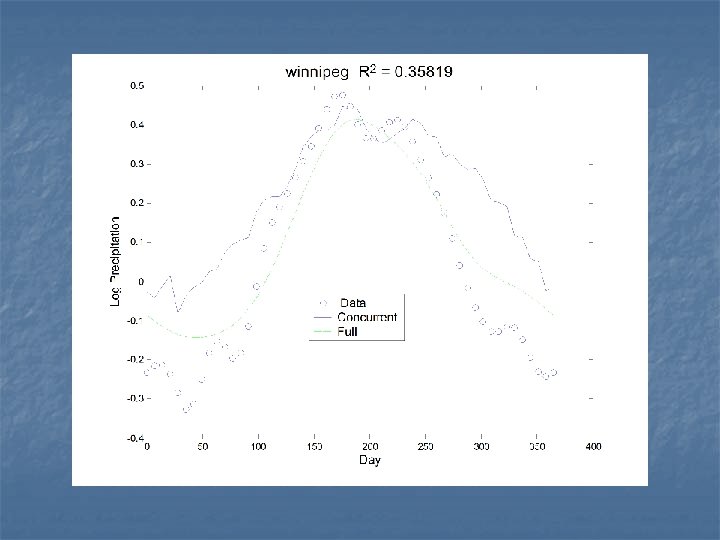
The concurrent model n This time, we’ll only use temperature at time t to predict precipitation at time t:

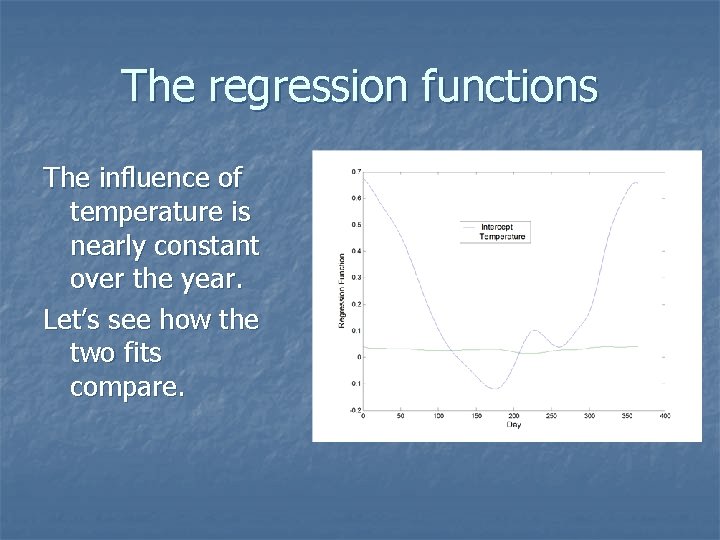
The regression functions The influence of temperature is nearly constant over the year. Let’s see how the two fits compare.

The historical linear model n n When the functions are not periodic, it may not be reasonable to assume that x(s) can influence y(t) when s > t. The historical linear model is described in Applied Functional Data Analysis, and in talk at this conference by Nicole Malfait.

The concurrent model and differential equations n n One important extension of the concurrent model is to the fitting of data by a differential equation. A simple example is