Discrete models Types of discrete models Binary models

Discrete models

Types of discrete models � Binary models Logit and Probit � Binary models with correlation (multivariate) � Multinomial non ordered � Ordered models (rankings) � Count models (patents)

We focus on binary models � Refer to Greene chapter (also uploaded in the site) and Montini document on fit measures. � Microeconometrics � Consumer � Random choices (but not only) utility framework (linked to Hicksian theory). . You observe what people choose, they choose what the like the best





Cdf= cumulative density function



Mean and variance for Bernoulli random var � In deciding on the estimation technique, it is useful to derive the conditional mean and variance � E(y/x)= B 0 + B 1 x 1 + B 2 x 2 +……Bkxk � Var (y/x)= XB(1 - XB), where XB is B 0 + B 1 x 1 + B 2 x 2 +……Bkxk. � OLS produces consistent and even unbiased estimates, BUT… � Heteroskedasticity is always an issue to be dealt by weighted least squares (het in stata)

HET � Always recall that HET affects s. e. not size of coefficients. . Correction should improve T ratios since it lower variances


Linear probability model for binary models � P(y=1/X)= B 0 + B 1 x 1 + B 2 x 2 +……Bkxk � B 1= d. P(y=1)/dx 1, assuming x 1 is not related functionally to other covariates, B 1 is the change in the probability of success given a one unit increase in x 1. holding other Xj fixed � Unless x is restricted, the LPM cannot be a good description of the population response probability � There are values of Bx for which P is outside the unit 0 -1 interval
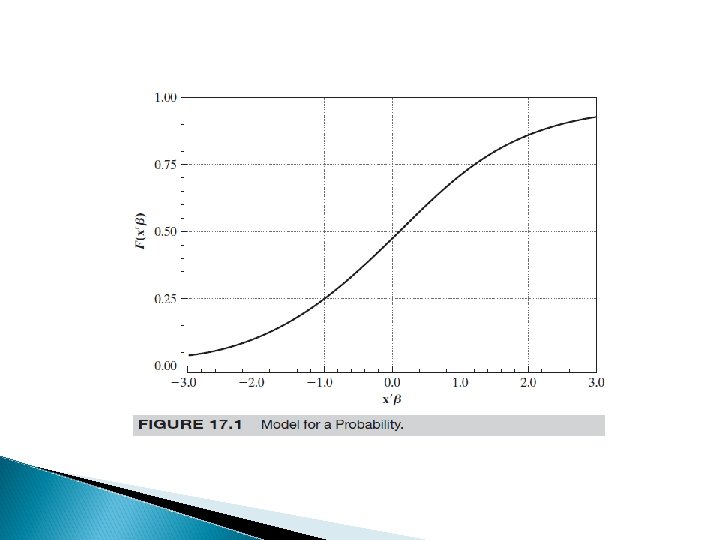

LPM then not usable � So what? We ve to find a model coherent with a probability framework � Here LOGIT and PROBIT enters

Used in MNL contexts


The sign is given by the sign of B See Mancinelli, Mazzanti, Ponti and Rizza (2010), J of socio economics, also WP DEIT Non siamo in un contesto dove possiamo rappresentare B come elasticità, questo è vero anche in modelli lin-log, dove ad esempio la var dipendente (causa ‘ 0’ diffusi) non può essere rappresentata in log.

Elasticity Linear model Dy/dx = b; e=b*x/y Log log Dlny/dlnx= b*y/x E=b Lin log Dy/dlnx = b*1/x E= b*x/y= b/y

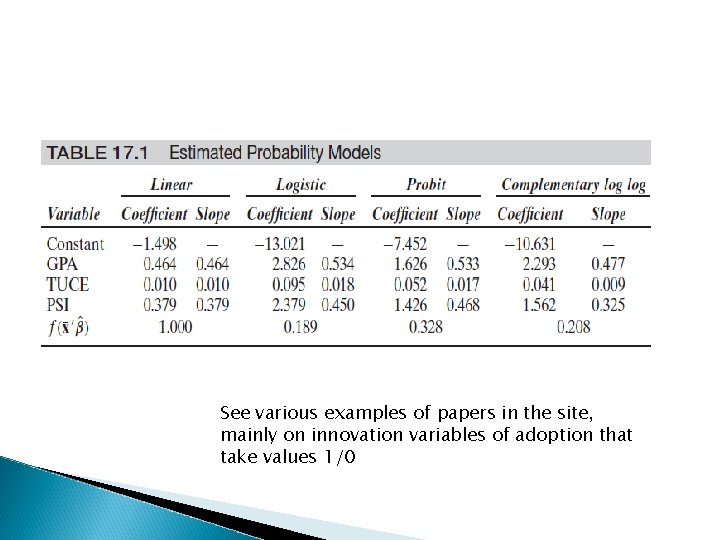
See various examples of papers in the site, mainly on innovation variables of adoption that take values 1/0
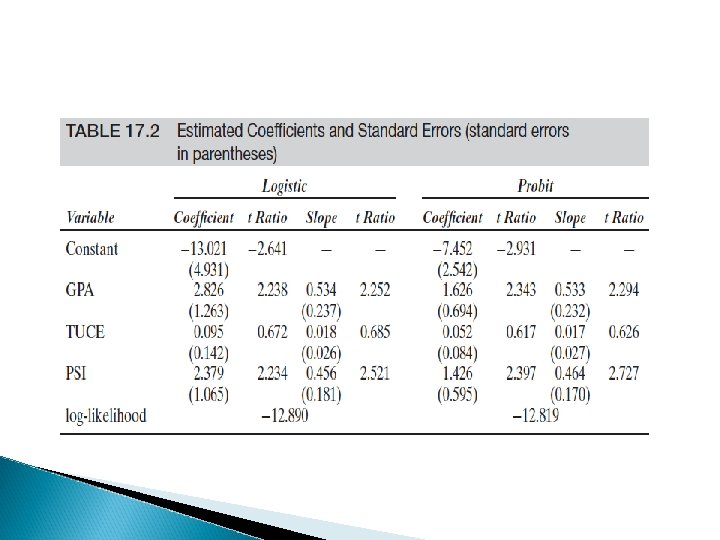

Practical issues to interpret estimates � Coefficient fo not represent marginal effects ◦ You can use dprobit in STATA for that � R 2 is not a measure of fit, we have pseudo R 2, es. Mc. Fadden R 2 (see Montini document on that) � You should have good F test, reasonable R 2 (0. 2 excellent, but 0. 05 fine as well), a set of *** coefficients.

Goodness of fit See Montini chapter
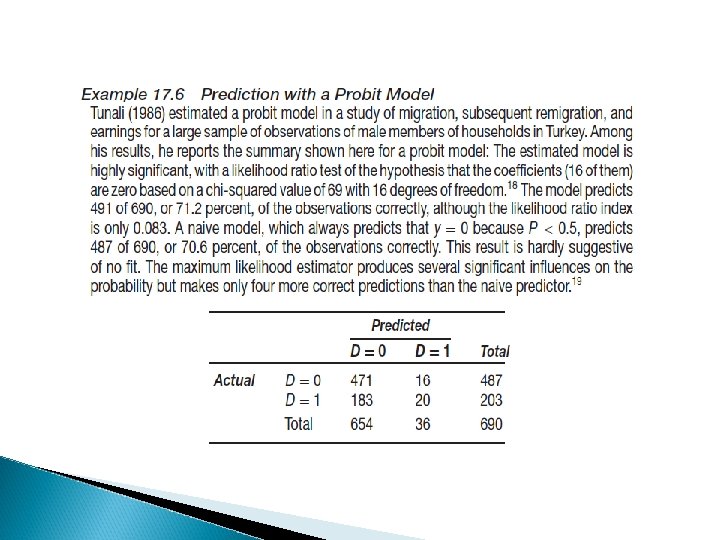


Two stage Heckman � Es. R&D, labor hours offered � First stage probit, then OLS � Get the inverse Mills ratio from first to inform the second and see whether the bias is there � Heckman vs Tobit models (different assumptions)

2 stage Heckman or heckit model: sample selection � Y 1= X 1 B 1 + u 1 � Y 2= 1(x 2 + v 2 >0) � Hp: x, y 2 always observed, y 1 only if y 2=1, set to 0 if y 2=0 � E(y 1/X, y 2=1) = x 1 B 1 + (x 2) � OLS can produce biased inconsistent estimates of B 1 if we do not account for the last term � OMITTED VAR problem

� We need an estimator of 2! � Obtain the probit estimates of 2 from first stage P(y 2=1/x) = (x 2) using all N units � Then estimate Inverse Mills ratio, = f(x 2) � Insert IMR in the OLS second equation and get B and estimates � These estimators are consistent

� X 1 covariates of OLS, X of probit � ** we dont need x 1 to be a subset of X for identification. But X=X 1 can introduce collinearity since can be approximated by a linear function of X � Example in Wooldridge, Econometric analysis of cross section and panel data, p. 565 (wage equation for married women) � Estimates become imprecise when X=x 1
- Slides: 31