FiveMinute Check over Chapter 5 CCSS ThenNow New






































 and [g ○ f](x) for f(x) = Compose Functions B. Find [f ○ g](x) and [g ○ f](x) for f(x) =](https://slidetodoc.com/presentation_image_h2/3af66829632667d5d49dd7ec1577d0a1/image-39.jpg)





 and [g ○ f](x) for f(x) = x 2 B. Find [f ○ g](x) and [g ○ f](x) for f(x) = x 2](https://slidetodoc.com/presentation_image_h2/3af66829632667d5d49dd7ec1577d0a1/image-45.jpg)
 and [g ○ f](x) for f(x) = x 2 B. Find [f ○ g](x) and [g ○ f](x) for f(x) = x 2](https://slidetodoc.com/presentation_image_h2/3af66829632667d5d49dd7ec1577d0a1/image-46.jpg)








- Slides: 54


Five-Minute Check (over Chapter 5) CCSS Then/Now New Vocabulary Key Concept: Operations on Functions Example 1: Add and Subtract Functions Example 2: Multiply and Divide Functions Key Concept: Composition of Functions Example 3: Compose Functions Example 4: Real-World Example: Use Composition of Functions

Over Chapter 5 Estimate the x-coordinates at which the relative maxima and relative minima occur for the graph of f(x) = x 4 + 16 x 2 – 25. A. 0 B. 1 C. 4 D. 5

Over Chapter 5 Estimate the x-coordinates at which the relative maxima and relative minima occur for the graph of f(x) = x 4 + 16 x 2 – 25. A. 0 B. 1 C. 4 D. 5

Over Chapter 5 Solve p 3 – 2 p 2 – 8 p = 0. A. – 2, 2 B. – 2, 0, 4 C. 0, 2, 6 D. 2, 4, 6

Over Chapter 5 Solve p 3 – 2 p 2 – 8 p = 0. A. – 2, 2 B. – 2, 0, 4 C. 0, 2, 6 D. 2, 4, 6

Over Chapter 5 Solve x 4 – 7 x 2 + 12 = 0. A. B. C. D.

Over Chapter 5 Solve x 4 – 7 x 2 + 12 = 0. A. B. C. D.

Over Chapter 5 Which is not a possible rational zero for the function f(x) = 3 x 3 – 12 x 2 – 5 x + 15? A. ± 15 B. C. D.

Over Chapter 5 Which is not a possible rational zero for the function f(x) = 3 x 3 – 12 x 2 – 5 x + 15? A. ± 15 B. C. D.

Over Chapter 5 Which of the following could not be a zero of the function g(x) = 4 x 3 – 5 x + 26? A. B. 1 C. 4 D. 13

Over Chapter 5 Which of the following could not be a zero of the function g(x) = 4 x 3 – 5 x + 26? A. B. 1 C. 4 D. 13

Content Standards F. IF. 9 Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions). F. BF. 1. b Combine standard function types using arithmetic operations. Mathematical Practices 2 Reason abstractly and quantitatively.

You performed operations on polynomials. • Find the sum, difference, product, and quotient of functions. • Find the composition of functions.

• composition of functions


Add and Subtract Functions A. Given f(x) = 3 x 2 + 7 x and g(x) = 2 x 2 – x – 1, find (f + g)(x) = f(x) + g(x) Answer: Addition of functions = (3 x 2 + 7 x) + (2 x 2 – x – 1) f(x) = 3 x 2 + 7 x and g(x) = 2 x 2 – x – 1 = 5 x 2 + 6 x – 1 Simplify.

Add and Subtract Functions A. Given f(x) = 3 x 2 + 7 x and g(x) = 2 x 2 – x – 1, find (f + g)(x) = f(x) + g(x) Addition of functions = (3 x 2 + 7 x) + (2 x 2 – x – 1) f(x) = 3 x 2 + 7 x and g(x) = 2 x 2 – x – 1 = 5 x 2 + 6 x – 1 Simplify. Answer: 5 x 2 + 6 x – 1

Add and Subtract Functions B. Given f(x) = 3 x 2 + 7 x and g(x) = 2 x 2 – x – 1, find (f – g)(x) = f(x) – g(x) Answer: Subtraction of functions = (3 x 2 + 7 x) – (2 x 2 – x – 1) f(x) = 3 x 2 + 7 x and g(x) = 2 x 2 – x – 1 = x 2 + 8 x + 1 Simplify.

Add and Subtract Functions B. Given f(x) = 3 x 2 + 7 x and g(x) = 2 x 2 – x – 1, find (f – g)(x) = f(x) – g(x) Subtraction of functions = (3 x 2 + 7 x) – (2 x 2 – x – 1) f(x) = 3 x 2 + 7 x and g(x) = 2 x 2 – x – 1 = x 2 + 8 x + 1 Simplify. Answer: x 2 + 8 x + 1

A. Given f(x) = 2 x 2 + 5 x + 2 and g(x) = 3 x 2 + 3 x – 4, find (f + g)(x). A. 5 x 2 + 8 x – 2 B. 5 x 2 + 8 x + 6 C. x 2 – 2 x – 6 D. 5 x 4 + 8 x 2 – 2

A. Given f(x) = 2 x 2 + 5 x + 2 and g(x) = 3 x 2 + 3 x – 4, find (f + g)(x). A. 5 x 2 + 8 x – 2 B. 5 x 2 + 8 x + 6 C. x 2 – 2 x – 6 D. 5 x 4 + 8 x 2 – 2

B. Given f(x) = 2 x 2 + 5 x + 2 and g(x) = 3 x 2 + 3 x – 4, find (f – g)(x). A. –x 2 + 2 x + 5 B. x 2 – 2 x – 6 C. –x 2 + 2 x – 2 D. –x 2 + 2 x + 6

B. Given f(x) = 2 x 2 + 5 x + 2 and g(x) = 3 x 2 + 3 x – 4, find (f – g)(x). A. –x 2 + 2 x + 5 B. x 2 – 2 x – 6 C. –x 2 + 2 x – 2 D. –x 2 + 2 x + 6

Multiply and Divide Functions A. Given f(x) = 3 x 2 – 2 x + 1 and g(x) = x – 4, find (f ● g)(x) = f(x) ● g(x) = (3 x 2 – 2 x + 1)(x – 4) Product of functions Substitute. = 3 x 2(x – 4) – 2 x(x – 4) + 1(x – 4) Distributive Property Answer: = 3 x 3 – 12 x 2 – 2 x 2 + 8 x + x – 4 Distributive Property = 3 x 3 – 14 x 2 + 9 x – 4 Simplify.

Multiply and Divide Functions A. Given f(x) = 3 x 2 – 2 x + 1 and g(x) = x – 4, find (f ● g)(x) = f(x) ● g(x) = (3 x 2 – 2 x + 1)(x – 4) Product of functions Substitute. = 3 x 2(x – 4) – 2 x(x – 4) + 1(x – 4) Distributive Property = 3 x 3 – 12 x 2 – 2 x 2 + 8 x + x – 4 = 3 x 3 – 14 x 2 + 9 x – 4 Answer: 3 x 3 – 14 x 2 + 9 x – 4 Distributive Property Simplify.

Multiply and Divide Functions B. Given f(x) = 3 x 2 – 2 x + 1 and g(x) = x – 4, find Division of functions f(x) = 3 x 2 – 2 x + 1 and g(x) = x – 4 Answer:

Multiply and Divide Functions B. Given f(x) = 3 x 2 – 2 x + 1 and g(x) = x – 4, find Division of functions f(x) = 3 x 2 – 2 x + 1 and g(x) = x – 4 Answer:

Multiply and Divide Functions Since 4 makes the denominator 0, it is excluded from the domain of

A. Given f(x) = 2 x 2 + 3 x – 1 and g(x) = x + 2, find (f ● g)(x). A. 2 x 3 + 3 x 2 – x + 2 B. 2 x 3 + 3 x – 2 C. 2 x 3 + 7 x 2 + 5 x – 2 D. 2 x 3 + 7 x 2 + 7 x + 2

A. Given f(x) = 2 x 2 + 3 x – 1 and g(x) = x + 2, find (f ● g)(x). A. 2 x 3 + 3 x 2 – x + 2 B. 2 x 3 + 3 x – 2 C. 2 x 3 + 7 x 2 + 5 x – 2 D. 2 x 3 + 7 x 2 + 7 x + 2

B. Given f(x) = 2 x 2 + 3 x – 1 and g(x) = x + 2, find. A. B. C. D.

B. Given f(x) = 2 x 2 + 3 x – 1 and g(x) = x + 2, find. A. B. C. D.


Compose Functions A. If f(x) = (2, 6), (9, 4), (7, 7), (0, – 1) and g(x) = (7, 0), (– 1, 7), (4, 9), (8, 2) , find [f ○ g](x) and [g ○ f](x). To find f ○ g, evaluate g(x) first. Then use the range of g as the domain of f and evaluate f(x). f[g(7)] = f(0) or – 1 g(7) = 0 f[g(– 1)] = f(7) or 7 g(– 1) = 7 f[g(4)] = f(9) or 4 g(4) = 9 f[g(8)] = f(2) or 6 g(8) = 2 Answer:

Compose Functions A. If f(x) = (2, 6), (9, 4), (7, 7), (0, – 1) and g(x) = (7, 0), (– 1, 7), (4, 9), (8, 2) , find [f ○ g](x) and [g ○ f](x). To find f ○ g, evaluate g(x) first. Then use the range of g as the domain of f and evaluate f(x). f[g(7)] = f(0) or – 1 g(7) = 0 f[g(– 1)] = f(7) or 7 g(– 1) = 7 f[g(4)] = f(9) or 4 g(4) = 9 f[g(8)] = f(2) or 6 g(8) = 2 Answer: f ○ g = {(7, – 1), (– 1, 7), (4, 4), (8, 6)}

Compose Functions To find g ○ f, evaluate f(x) first. Then use the range of f as the domain of g and evaluate g(x). g[f(2)] = g(6) is undefined. g[f(9)] = g(4) or 9 f(9) = 4 g[f(7)] = g(7) or 0 f(7) = 7 g[f(0)] = g(– 1) or 7 f(0) = – 1 Answer:

Compose Functions To find g ○ f, evaluate f(x) first. Then use the range of f as the domain of g and evaluate g(x). g[f(2)] = g(6) is undefined. g[f(9)] = g(4) or 9 f(9) = 4 g[f(7)] = g(7) or 0 f(7) = 7 g[f(0)] = g(– 1) or 7 f(0) = – 1 Answer: Since 6 is not in the domain of g, g ○ f is undefined for x = 2. g ○ f = {(9, 9), (7, 0), (0, 7)}
 and [g ○ f](x) for f(x) =](https://slidetodoc.com/presentation_image_h2/3af66829632667d5d49dd7ec1577d0a1/image-39.jpg)
Compose Functions B. Find [f ○ g](x) and [g ○ f](x) for f(x) = 3 x 2 – x + 4 and g(x) = 2 x – 1. State the domain and range for each combined function. [f ○ g](x) = f[g(x)] Composition of functions = f(2 x – 1) Replace g(x) with 2 x – 1. = 3(2 x – 1)2 – (2 x – 1) + 4 Substitute 2 x – 1 for x in f(x).

Compose Functions = 3(4 x 2 – 4 x + 1) – 2 x + 1 + 4 Evaluate (2 x – 1)2. = 12 x 2 – 14 x + 8 Simplify. [g ○ f](x) = g[f(x)] = g(3 x 2 – x + 4) Composition of functions Replace f(x) with 3 x 2 – x + 4.

Compose Functions Answer: = 2(3 x 2 – x + 4) – 1 Substitute 3 x 2 – x + 4 for x in g(x). = 6 x 2 – 2 x + 7 Simplify.

Compose Functions = 2(3 x 2 – x + 4) – 1 Substitute 3 x 2 – x + 4 for x in g(x). = 6 x 2 – 2 x + 7 Simplify. Answer: So, [f ○ g](x) = 12 x 2 – 14 x + 8; D = {all real numbers}, R = {y│y > 3. 91}; and [g ○ f](x) = 6 x 2 – 2 x + 7; D = {all real numbers}, R = {y│y > 6. 33}.


 and [g ○ f](x) for f(x) = x 2](https://slidetodoc.com/presentation_image_h2/3af66829632667d5d49dd7ec1577d0a1/image-45.jpg)
B. Find [f ○ g](x) and [g ○ f](x) for f(x) = x 2 + 2 x + 3 and g(x) = x + 5. State the domain and range for each combined function. A. [f ○ g](x) = x 2 + 2 x + 8; D = {all real numbers}, R = {y│y ≥ 2}; and [g ○ f](x) = x 2 + 12 x + 38; D = {all real numbers}, R = {y│y ≥ 7} B. [f ○ g](x) = x 2 + 12 x + 38; D = {all real numbers}, R = {y│y ≥ 7}; and [g ○ f](x) = x 2 + 12 x + 38; D = {all real numbers}, R = {y│y ≥ 2} C. [f ○ g](x) = x 2 + 12 x + 38; D = {all real numbers}, R = {y│y ≥ 2}; and [g ○ f](x) = x 2 + 2 x + 8; D = {all real numbers}, R = {y│y ≥ 7}
 and [g ○ f](x) for f(x) = x 2](https://slidetodoc.com/presentation_image_h2/3af66829632667d5d49dd7ec1577d0a1/image-46.jpg)
B. Find [f ○ g](x) and [g ○ f](x) for f(x) = x 2 + 2 x + 3 and g(x) = x + 5. State the domain and range for each combined function. A. [f ○ g](x) = x 2 + 2 x + 8; D = {all real numbers}, R = {y│y ≥ 2}; and [g ○ f](x) = x 2 + 12 x + 38; D = {all real numbers}, R = {y│y ≥ 7} B. [f ○ g](x) = x 2 + 12 x + 38; D = {all real numbers}, R = {y│y ≥ 7}; and [g ○ f](x) = x 2 + 12 x + 38; D = {all real numbers}, R = {y│y ≥ 2} C. [f ○ g](x) = x 2 + 12 x + 38; D = {all real numbers}, R = {y│y ≥ 2}; and [g ○ f](x) = x 2 + 2 x + 8; D = {all real numbers}, R = {y│y ≥ 7}

Use Composition of Functions TAXES Hector has $100 deducted from every paycheck for retirement. He can have this deduction taken before state taxes are applied, which reduces his taxable income. His state income tax is 4%. If Hector earns $1500 every pay period, find the difference in his net income if he has the retirement deduction taken before or after state taxes. Understand Let x = his income per paycheck, r(x) = his income after the deduction for retirement, and t(x) = his income after the deduction for state income tax.

Use Composition of Functions Plan Write equations for r(x) and t(x). $100 is deducted for retirement. r(x) = x – 100 The tax rate is 4%. Solve t(x) = x – 0. 04 x If Hector has his retirement deducted before taxes, then his net income is represented by [t ○ r](1500)= t(1500 – 100) = t(1400) Replace x with 1500 in r(x) = x – 100.

Use Composition of Functions = 1400 – 0. 04(1400) Replace x with 1400 in t(x) = x – 0. 04 x. = 1344 If Hector has his retirement deducted after taxes, then his net income is represented by [r ○ t](1500). Replace x with 1500 in t(x) = x – 0. 04 x. [r ○ t](1500) = r[1500 – 0. 04(1500)] = r(1500 – 60) = r(1440)

Use Composition of Functions = 1440 – 100 = 1340 Answer: Replace x with 1440 in r(x) = x – 100.

Use Composition of Functions = 1440 – 100 Replace x with 1440 in r(x) = x – 100. = 1340 Answer: [t ○ r](1500) = 1344 and [r ○ t](1500) = 1340. The difference is 1344 – 1340 or 4. So, his net income is $4 more if the retirement deduction is taken before taxes.

TAXES Brandi Smith has $200 deducted from every paycheck for retirement. She can have this deduction taken before state taxes are applied, which reduces her taxable income. Her state income tax is 10%. If Brandi earns $2200 every pay period, find the difference in her net income if she has the retirement deduction taken before state taxes. A. Her net income is $20 less if she has the retirement deduction taken before her state taxes. B. Her net income is $20 more if she has the retirement deduction taken before her state taxes. C. Her net income is $10 less if she has the retirement deduction taken before her state taxes. D. Her net income is $10 more if she has the retirement deduction taken before her state taxes.

TAXES Brandi Smith has $200 deducted from every paycheck for retirement. She can have this deduction taken before state taxes are applied, which reduces her taxable income. Her state income tax is 10%. If Brandi earns $2200 every pay period, find the difference in her net income if she has the retirement deduction taken before state taxes. A. Her net income is $20 less if she has the retirement deduction taken before her state taxes. B. Her net income is $20 more if she has the retirement deduction taken before her state taxes. C. Her net income is $10 less if she has the retirement deduction taken before her state taxes. D. Her net income is $10 more if she has the retirement deduction taken before her state taxes.

 Ccss app
Ccss app Hormofen y ciclotab 20
Hormofen y ciclotab 20 Ccss
Ccss Gerencia de pensiones ccss
Gerencia de pensiones ccss Ccss splash
Ccss splash Test de tamizaje para adolescentes de la ccss
Test de tamizaje para adolescentes de la ccss Ccss jpams
Ccss jpams Behavior check in check out sheet
Behavior check in check out sheet Behavior check in check out sheet
Behavior check in check out sheet Check in check out behavior intervention
Check in check out behavior intervention Check in check out system for students
Check in check out system for students Cashiers check bank of america
Cashiers check bank of america Character generation methods in computer graphics
Character generation methods in computer graphics Checkin checkout system
Checkin checkout system Check-in/check-out intervention template
Check-in/check-out intervention template Collision forces quick check
Collision forces quick check Endorsing a check to someone else
Endorsing a check to someone else Check my progress vocabulary check
Check my progress vocabulary check Non depository institutions
Non depository institutions Over the mountains over the plains
Over the mountains over the plains Siach reciting the word over and over
Siach reciting the word over and over Taking over navigational watch
Taking over navigational watch Chapter 16 toward a new heaven and a new earth
Chapter 16 toward a new heaven and a new earth An endorsement consisting only of the endorser's signature
An endorsement consisting only of the endorser's signature Paid cash to replenish the petty cash fund
Paid cash to replenish the petty cash fund Yun.ir refah new check
Yun.ir refah new check As new industrialism swept over the land
As new industrialism swept over the land Equanimity sentence
Equanimity sentence Ten words in context chapter 3
Ten words in context chapter 3 Improving vocabulary skills 5th edition
Improving vocabulary skills 5th edition Chapter 12 banking procedures and services
Chapter 12 banking procedures and services Chapter 16 ten words in context
Chapter 16 ten words in context Chapter 28 sentence check 1
Chapter 28 sentence check 1 Chapter 13 ten words in context sentence check 2 answers
Chapter 13 ten words in context sentence check 2 answers Ten word parts in context chapter 6
Ten word parts in context chapter 6 Chapter 7 sentence check 2 answer key
Chapter 7 sentence check 2 answer key Chapter 23 sentence check 2
Chapter 23 sentence check 2 Chapter 17 vocabulary sentence check 1
Chapter 17 vocabulary sentence check 1 Chapter 12 sentence check 1
Chapter 12 sentence check 1 Chapter 10 sentence check 2 answer key
Chapter 10 sentence check 2 answer key Chapter 11 sentence check 2 clandestine
Chapter 11 sentence check 2 clandestine Chapter 10 sentence check 2
Chapter 10 sentence check 2 Chapter 8 sentence check 2 answers key attrition
Chapter 8 sentence check 2 answers key attrition Chapter 14 sentence check 1 austere
Chapter 14 sentence check 1 austere Improving vocabulary skills 4th edition answer key
Improving vocabulary skills 4th edition answer key Chapter 7 sentence check 2 answer key clamor
Chapter 7 sentence check 2 answer key clamor Advanced word power answer key
Advanced word power answer key Section quick check chapter 10 section 1 meiosis answer key
Section quick check chapter 10 section 1 meiosis answer key Examples of inverted commas
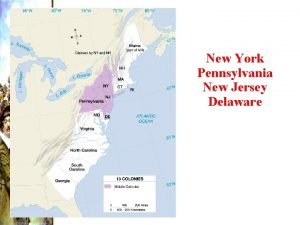
Examples of inverted commas New york, new jersey, pennsylvania, and delaware
New york, new jersey, pennsylvania, and delaware Fresh oil, new wine scripture
Fresh oil, new wine scripture Marquee cinema
Marquee cinema 3 weaknesses of the articles of confederation
3 weaknesses of the articles of confederation New-old approach to creating new ventures
New-old approach to creating new ventures New consumer capabilities and new company capabilities
New consumer capabilities and new company capabilities