Financial Engineering Zvi Wiener mswienermscc huji ac il








![Primary Asset Valuation Needs["Statistics`Normal. Distribution`"] nor[mu_, sig_]: =Random[Normal. Distribution[mu, sig]]; tt=Nest. List[ (#+nor[0, 0. Primary Asset Valuation Needs["Statistics`Normal. Distribution`"] nor[mu_, sig_]: =Random[Normal. Distribution[mu, sig]]; tt=Nest. List[ (#+nor[0, 0.](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-9.jpg)
![Main Properties 1. E[d. W(t)] = 0 2. E[d. W(t) dt] = E[d. W(t)] Main Properties 1. E[d. W(t)] = 0 2. E[d. W(t) dt] = E[d. W(t)]](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-11.jpg)
![Main Properties (cont. ) 4. Var[d. W(t)2] = E[d. W(t)4] - E 2[d. W(t)2] Main Properties (cont. ) 4. Var[d. W(t)2] = E[d. W(t)4] - E 2[d. W(t)2]](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-12.jpg)
![E[d. W(t)] = 0 By definition the mean of the normally distributed variable is E[d. W(t)] = 0 By definition the mean of the normally distributed variable is](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-13.jpg)
![E[d. W(t) dt] = E[d. W(t)] dt = 0 The expectation of the product E[d. W(t) dt] = E[d. W(t)] dt = 0 The expectation of the product](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-14.jpg)
![E[d. W(t)2] = dt For any distribution with zero mean the expected value of E[d. W(t)2] = dt For any distribution with zero mean the expected value of](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-15.jpg)
![2 Var[d. W(t) ] 4 E[d. W(t) ] - = 2 2 E [d. 2 Var[d. W(t) ] 4 E[d. W(t) ] - = 2 2 E [d.](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-16.jpg)
![E[(d. W(t)dt)2] = E [d. W(t)2] (dt)2 = 0 Follows from properties 2 and E[(d. W(t)dt)2] = E [d. W(t)2] (dt)2 = 0 Follows from properties 2 and](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-17.jpg)
![Var[d. W(t)dt] = 4 2 E[(d. W(t)dt) ] - E [d. W(t)dt] = 0 Var[d. W(t)dt] = 4 2 E[(d. W(t)dt) ] - E [d. W(t)dt] = 0](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-18.jpg)
![Important Property if Var[f(d. W)] = 0 then E[f(d. W)] = f(d. W) Zvi Important Property if Var[f(d. W)] = 0 then E[f(d. W)] = f(d. W) Zvi](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-19.jpg)






















![Mean Reverting Process d. X = ( -X)dt + X d. W Seed. Random[2] Mean Reverting Process d. X = ( -X)dt + X d. W Seed. Random[2]](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-47.jpg)









![Financial Applications A Vt = r. V - 1 DSolve[ V'[t]==r*V[t]-1, V[t], t ] Financial Applications A Vt = r. V - 1 DSolve[ V'[t]==r*V[t]-1, V[t], t ]](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-57.jpg)


![Financial Applications B 2. The expected capital gain: ECG = E[d. V] = [ Financial Applications B 2. The expected capital gain: ECG = E[d. V] = [](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-60.jpg)


- Slides: 62

Financial Engineering Zvi Wiener mswiener@mscc. huji. ac. il tel: 02 -588 -3049 Zvi Wiener Cont. Time. Fin - 1 1

Main Books Shimko D. Finance in Continuous Time, A Primer. Kolb Publishing Company, 1992, ISBN 1 -878975 -07 -2 F Wilmott P. , S. Howison, J. Dewynne, The Mathematics of Financial Derivatives, A Student Introduction, Cambridge University Press, 1996, ISBN 0 -521 -49789 -2 F Zvi Wiener Cont. Time. Fin - 1 2

Useful Books Duffie D. , Dynamic Asset Pricing Theory. F Duffie D. , Security Markets, Stochastic Models. F Neftci S. , An Introduction to the Mathematics of Financial Derivatives. F Steele M. , Invitation to Stochastic Differential Equations and Financial Applications. F Karatzas I. , and S. Shreve, BM and Stochastic Calculus. F Zvi Wiener Cont. Time. Fin - 1 3

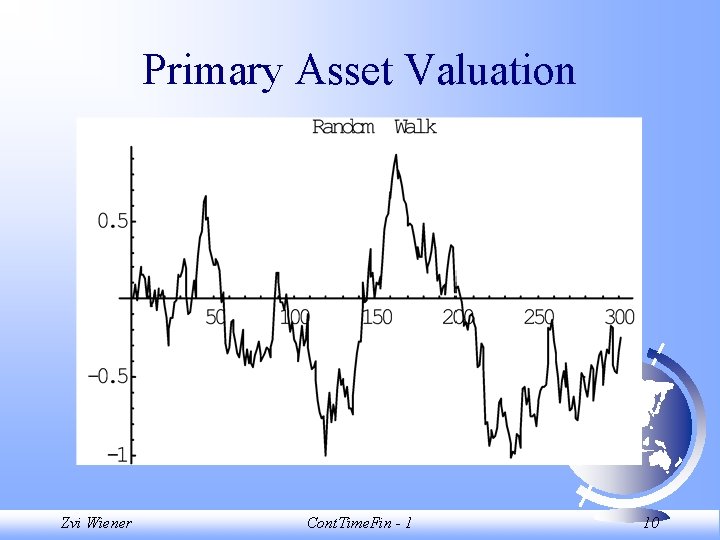
Primary Asset Valuation Discrete-time random walk: W(t+1) = W(t) + e(t+1); W(0) = W 0; e~i. i. d. N(0, 1) Zvi Wiener Cont. Time. Fin - 1 4

Primary Asset Valuation N(0, 1) Zvi Wiener Cont. Time. Fin - 1 5

Primary Asset Valuation Discrete-time random walk refinement: W(t+ ) = W(t) + e(t+ ); W(0) = W 0; e~i. i. d. N(0, ) This process has the same expected drift and variance over n periods as the initial process had in one period. Zvi Wiener Cont. Time. Fin - 1 6

Primary Asset Valuation t=0 Zvi Wiener 0. 25 0. 5 Cont. Time. Fin - 1 0. 75 N(0, 1) 1 7

Primary Asset Valuation Set dt W(t+ dt) = W(t) + e(t+ dt); W(0) = W 0; e~i. i. d. N(0, dt) Define d. W(t) = W(t+dt) - W(t) white noise, (dt)a = 0 for any a > 1 Zvi Wiener Cont. Time. Fin - 1 8
![Primary Asset Valuation NeedsStatisticsNormal Distribution normu sig RandomNormal Distributionmu sig ttNest List nor0 0 Primary Asset Valuation Needs["Statistics`Normal. Distribution`"] nor[mu_, sig_]: =Random[Normal. Distribution[mu, sig]]; tt=Nest. List[ (#+nor[0, 0.](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-9.jpg)
Primary Asset Valuation Needs["Statistics`Normal. Distribution`"] nor[mu_, sig_]: =Random[Normal. Distribution[mu, sig]]; tt=Nest. List[ (#+nor[0, 0. 1])&, 0, 300]; List. Plot[tt, Plot. Joined->True, Plot. Label->"Random Walk"]; Zvi Wiener Cont. Time. Fin - 1 9

Primary Asset Valuation Zvi Wiener Cont. Time. Fin - 1 10
![Main Properties 1 Ed Wt 0 2 Ed Wt dt Ed Wt Main Properties 1. E[d. W(t)] = 0 2. E[d. W(t) dt] = E[d. W(t)]](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-11.jpg)
Main Properties 1. E[d. W(t)] = 0 2. E[d. W(t) dt] = E[d. W(t)] dt = 0 3. E[d. W(t)2] = dt Zvi Wiener Cont. Time. Fin - 1 11
![Main Properties cont 4 Vard Wt2 Ed Wt4 E 2d Wt2 Main Properties (cont. ) 4. Var[d. W(t)2] = E[d. W(t)4] - E 2[d. W(t)2]](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-12.jpg)
Main Properties (cont. ) 4. Var[d. W(t)2] = E[d. W(t)4] - E 2[d. W(t)2] = 3 dt 2 - dt 2 = 0 5. E[(d. W(t)dt)2] = E [d. W(t)2] (dt)2 = 0 6. Var[d. W(t)dt] = E[(d. W(t)dt)4] - E 2[d. W(t)dt] = 0 Zvi Wiener Cont. Time. Fin - 1 12
![Ed Wt 0 By definition the mean of the normally distributed variable is E[d. W(t)] = 0 By definition the mean of the normally distributed variable is](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-13.jpg)
E[d. W(t)] = 0 By definition the mean of the normally distributed variable is zero. Zvi Wiener Cont. Time. Fin - 1 13
![Ed Wt dt Ed Wt dt 0 The expectation of the product E[d. W(t) dt] = E[d. W(t)] dt = 0 The expectation of the product](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-14.jpg)
E[d. W(t) dt] = E[d. W(t)] dt = 0 The expectation of the product of a random variable (d. W) and a constant (dt) equals the constant times the expected value of the random variable. Zvi Wiener Cont. Time. Fin - 1 14
![Ed Wt2 dt For any distribution with zero mean the expected value of E[d. W(t)2] = dt For any distribution with zero mean the expected value of](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-15.jpg)
E[d. W(t)2] = dt For any distribution with zero mean the expected value of the squared random variable is the same as its variance. Zvi Wiener Cont. Time. Fin - 1 15
![2 Vard Wt 4 Ed Wt 2 2 E d 2 Var[d. W(t) ] 4 E[d. W(t) ] - = 2 2 E [d.](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-16.jpg)
2 Var[d. W(t) ] 4 E[d. W(t) ] - = 2 2 E [d. W(t) ] = 3 dt 2 - dt 2 = 0 The fourth central moment of the standard normal distribution is 3, and (dt)2 = 0. Zvi Wiener Cont. Time. Fin - 1 16
![Ed Wtdt2 E d Wt2 dt2 0 Follows from properties 2 and E[(d. W(t)dt)2] = E [d. W(t)2] (dt)2 = 0 Follows from properties 2 and](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-17.jpg)
E[(d. W(t)dt)2] = E [d. W(t)2] (dt)2 = 0 Follows from properties 2 and 3. Zvi Wiener Cont. Time. Fin - 1 17
![Vard Wtdt 4 2 Ed Wtdt E d Wtdt 0 Var[d. W(t)dt] = 4 2 E[(d. W(t)dt) ] - E [d. W(t)dt] = 0](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-18.jpg)
Var[d. W(t)dt] = 4 2 E[(d. W(t)dt) ] - E [d. W(t)dt] = 0 Follows from properties 2 and 5. Zvi Wiener Cont. Time. Fin - 1 18
![Important Property if Varfd W 0 then Efd W fd W Zvi Important Property if Var[f(d. W)] = 0 then E[f(d. W)] = f(d. W) Zvi](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-19.jpg)
Important Property if Var[f(d. W)] = 0 then E[f(d. W)] = f(d. W) Zvi Wiener Cont. Time. Fin - 1 19

Multiplication Rules Rule 1. (d. W(t))2 = dt Rule 2. (d. W(t)) dt = 0 Rule 3. dt 2 = 0 Zvi Wiener Cont. Time. Fin - 1 20

W(t) is called a standard Wiener process, or a Brownian motion. Zvi Wiener Cont. Time. Fin - 1 21

Major Properties of W 1. W(t) is continuous in t. 2. W(t) is nowhere differentiable. 3. W(t) is a process of unbounded variation. 4. W(t) is a process of bounded quadratic variation. Zvi Wiener Cont. Time. Fin - 1 22

Major Properties of W 5. The conditional distribution of W(u) given W(t), for u > t, is normal with mean W(t) and variance (u-t). 6. The variance of a forecast W(u) increases indefinitely as u . Zvi Wiener Cont. Time. Fin - 1 23

Brownian Motion - BM The standard BM is useful since many general stochastic processes can be written in terms of W. X(t+1) = X(t) + (X(t), t) e(t+1) X(0) = X 0, e~i. i. d. N(0, 1) generalized drift Zvi Wiener heteroscedastisity (changing variance) Cont. Time. Fin - 1 24

Brownian Motion - BM Choose a shorter time interval : X(t+ ) = X(t) + (X(t), t) e(t+ ) X(0) = X 0, e~i. i. d. N(0, ) generalized drift Zvi Wiener heteroscedastisity (changing variance) Cont. Time. Fin - 1 25

Brownian Motion - BM As we let dt we see that d. X(t) = (X(t), t) dt + (X(t), t) d. W(t) X(0) = X 0 generalized univariate Wiener process, (diffusion). d. X = (X, t) dt + (X, t) d. W, Zvi Wiener Cont. Time. Fin - 1 X(0) = X 0 26

Interpretation How can we interpret the fact that d. X = dt + d. W the random variable d. X has local mean dt and local variance 2 dt. A discrete analogy is X = + z. Zvi Wiener Cont. Time. Fin - 1 27

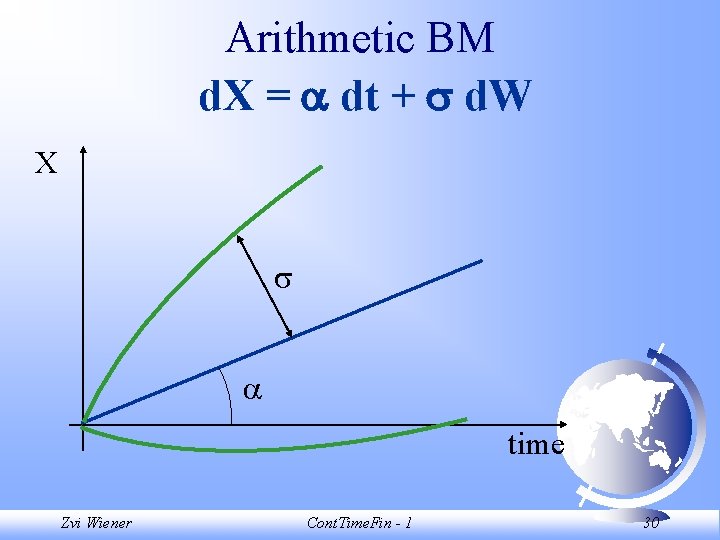
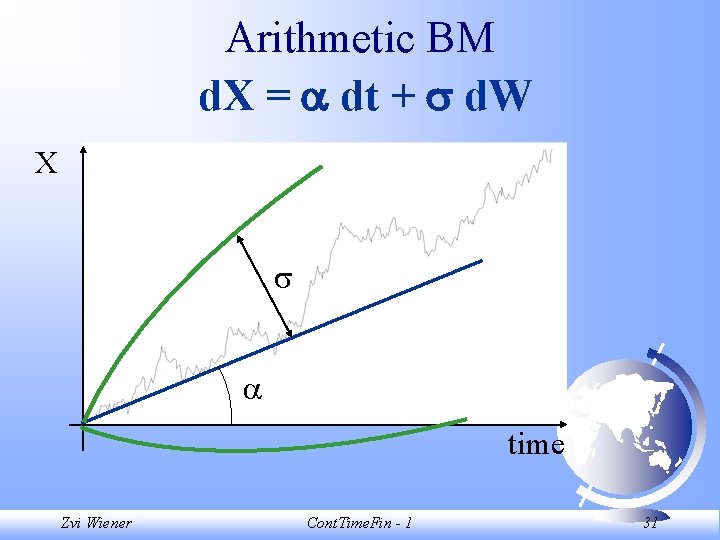
Arithmetic BM d. X = dt + d. W Let (X, t) = , and (X, t) = two constants. Then X follows an arithmetic Brownian Motion with drift and volatility . This is an appropriate specification for a process that grows at a linear rate and exhibits an increasing uncertainty. Zvi Wiener Cont. Time. Fin - 1 28

Arithmetic BM d. X = dt + d. W 1. X may be positive or negative. 2. If u > t, then Xu is a future value of the process relative to time t. The distribution of Xu given Xt is normal with mean Xt+ (u-t) and standard deviation (u-t)1/2. 3. The variance of a forecast Xu tends to infinity as u does (for fixed t and Xt). Zvi Wiener Cont. Time. Fin - 1 29

Arithmetic BM d. X = dt + d. W X time Zvi Wiener Cont. Time. Fin - 1 30

Arithmetic BM d. X = dt + d. W X time Zvi Wiener Cont. Time. Fin - 1 31

Arithmetic BM d. X = dt + d. W Is appropriate for variables that can be positive and negative, have normally distributed forecast errors, and have forecast variance increasing linearly in time. F Example: net cash flows. F Is inappropriate for stock price. F Zvi Wiener Cont. Time. Fin - 1 32

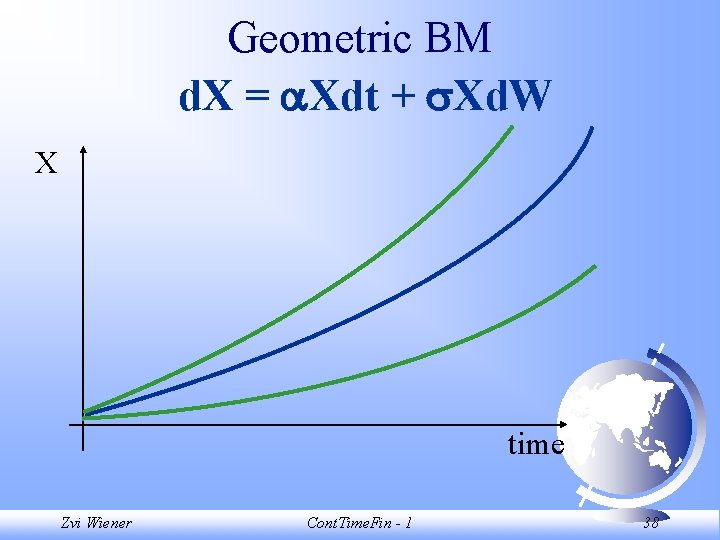
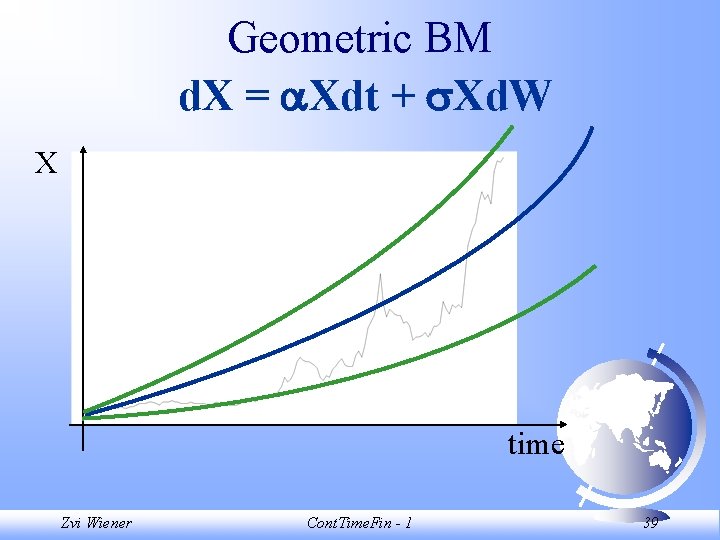
Geometric BM d. X = Xdt + Xd. W Let (X, t) = X, and (X, t) = X. Then X follows an geometric Brownian Motion. Zvi Wiener Cont. Time. Fin - 1 33

Geometric BM d. X = Xdt + Xd. W This is an appropriate specification for a process that F grows exponentially at an average rate of F has volatility proportional to the level of the variable. F It also exhibits an increasing uncertainty. Zvi Wiener Cont. Time. Fin - 1 34

Geometric BM d. X = Xdt + Xd. W 1. If X(0) > 0, it will always be positive. 2. X has an absorbing barrier at X = 0. Thus if X hits zero (a zero probability event) it will remain there forever. Zvi Wiener Cont. Time. Fin - 1 35

Geometric BM d. X = Xdt + Xd. W 3. The conditional distribution of Xu given Xt is lognormal. The conditional mean of ln(Xt) is ln(Xt) + (u-t) - 0. 5 2(u-t) and conditional standard deviation of ln(Xt) is (u-t)1/2. ln(Xt) is normally distributed. Zvi Wiener Cont. Time. Fin - 1 36

Geometric BM d. X = Xdt + Xd. W 4. The conditional expected value of Xu is Et[Xu] = Xtexp[ (u-t)] 5. The variance of a forecast Xu tends to infinity as u does (for fixed t and Xt). Zvi Wiener Cont. Time. Fin - 1 37

Geometric BM d. X = Xdt + Xd. W X time Zvi Wiener Cont. Time. Fin - 1 38

Geometric BM d. X = Xdt + Xd. W X time Zvi Wiener Cont. Time. Fin - 1 39

Geometric BM d. X = Xdt + Xd. W Is often used to model security values, since the proportional changes in security price are independent and identically normally distributed (sometimes). F Example: currency price, stocks. F Is inappropriate for dividends, interest rates. F Zvi Wiener Cont. Time. Fin - 1 40

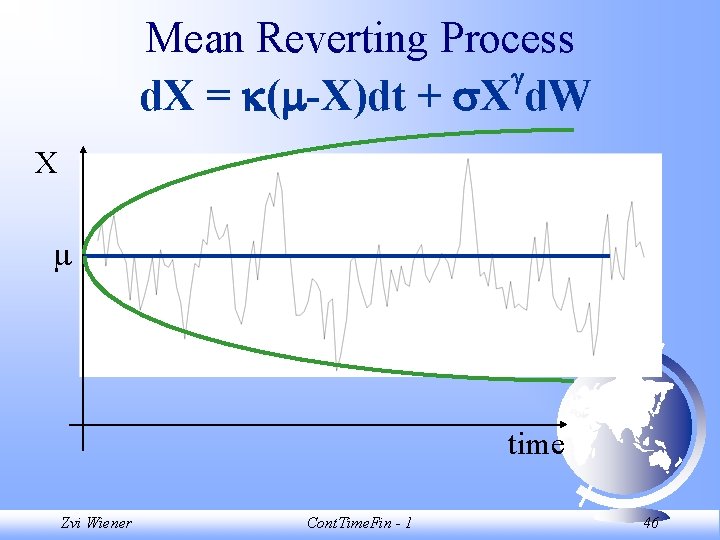
Mean Reverting Process d. X = ( -X)dt + X d. W Ornstein-Uhlenbeck when = 1 Let (X, t) = ( -X), and (X, t) = X , where 0 - speed of adjustment - long run mean - volatility Zvi Wiener Cont. Time. Fin - 1 41

Mean Reverting Process d. X = ( -X)dt + X d. W This is an appropriate specification for a process that has a long run value but may be beset by short -term disturbances. We assume that , , and are positive for simplicity. Zvi Wiener Cont. Time. Fin - 1 42

Mean Reverting Process d. X = ( -X)dt + X d. W 1. If X(0) > 0, it will always be positive. 2. As X approaches zero, the drift is positive and volatility vanishes. 3. As u becomes infinite, the variance of a forecast Xu is finite. Zvi Wiener Cont. Time. Fin - 1 43

Mean Reverting Process d. X = ( -X)dt + X d. W 4. If = 0. 5, the distribution of Xu given Xt for u > t is non-central chi-squared, the mean of the distribution is: (Xt- ) exp[- (u-t)] + the variance of the distribution is (CIR 85): Zvi Wiener Cont. Time. Fin - 1 44

Mean Reverting Process d. X = ( -X)dt + X d. W X time Zvi Wiener Cont. Time. Fin - 1 45

Mean Reverting Process d. X = ( -X)dt + X d. W X time Zvi Wiener Cont. Time. Fin - 1 46
![Mean Reverting Process d X Xdt X d W Seed Random2 Mean Reverting Process d. X = ( -X)dt + X d. W Seed. Random[2]](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-47.jpg)
Mean Reverting Process d. X = ( -X)dt + X d. W Seed. Random[2] tt=Nest. List[ (#+0. 3(1 -#)+0. 1*#*nor[0, 0. 1])&, 1. 01, 130]; List. Plot[tt, Plot. Joined->True, Axes->False]; Zvi Wiener Cont. Time. Fin - 1 47

Mean Reverting Process d. X = ( -X)dt + X d. W F Is often used to model economic variables and do not represent traded assets. F Example: interest rates, volatility. Zvi Wiener Cont. Time. Fin - 1 48

Ito’s lemma Consider a real valued function f(X): R R. Taylor series expansion: Zvi Wiener Cont. Time. Fin - 1 49

Ito’s lemma If X is a “standard” variable, then 2 is o( ) Zvi Wiener Cont. Time. Fin - 1 50

Ito’s lemma If X is a stochastic variable (following diffusion) then the term d. X 2 does NOT vanish. Zvi Wiener Cont. Time. Fin - 1 51

Ito’s lemma Zvi Wiener Cont. Time. Fin - 1 52

Ito’s lemma If f = f(X, t) and d. X = dt + d. W, then Zvi Wiener Cont. Time. Fin - 1 53

Financial Applications A Suppose that a security with value V guarantees $1 dt every instant of time forever. This is the continuous time equivalent of a risk-free perpetuity of $1. If the risk-free interest rate is constant r, what is the (discounted) value of the security? Zvi Wiener Cont. Time. Fin - 1 54

Financial Applications A 1. V = V(t), there are NO stochastic variables. d. V = Vtdt 2. The expected capital gain on V is ECG = E[d. V] = Vtdt 3. The expected cash flows to V is ECF = 1 dt 4. The total return on V is ECG + ECF = (Vt+1)dt Zvi Wiener Cont. Time. Fin - 1 55

Financial Applications A 5. Since there is no risk, the total return must be equal to the risk-free return on V, or r. Vdt. (Vt+1) dt = r V dt 6. Divide both sides by dt: Vt = r. V - 1 Zvi Wiener Cont. Time. Fin - 1 56
![Financial Applications A Vt r V 1 DSolve VtrVt1 Vt t Financial Applications A Vt = r. V - 1 DSolve[ V'[t]==r*V[t]-1, V[t], t ]](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-57.jpg)
Financial Applications A Vt = r. V - 1 DSolve[ V'[t]==r*V[t]-1, V[t], t ] V(t) = c Exp[r t] + 1/r given V(0) one can find c Zvi Wiener Cont. Time. Fin - 1 57

Financial Applications B Suppose that X follows a geometric Brownian motion with drift and volatility . A security with value V collects Xdt continuously forever. V represents a perpetuity that grows at an average exponential rate of , but whose risks in cash flow variations are considered diversificable. The economy is risk-neutral, and the risk-free interest rate is constant at r. What is the value of this security? Zvi Wiener Cont. Time. Fin - 1 58

Financial Applications B 1. V = V(X), since V is a perpetual claim, its price does not depend on time. d. V = Vxd. X + 0. 5 Vxxd. X 2, d. X = Xdt + Xd. W, d. X 2= 2 X 2 dt d. V = [ XVx+0. 5 2 X 2 Vxx]dt + XVxd. W Zvi Wiener Cont. Time. Fin - 1 59
![Financial Applications B 2 The expected capital gain ECG Ed V Financial Applications B 2. The expected capital gain: ECG = E[d. V] = [](https://slidetodoc.com/presentation_image_h/b7b22a31fa25c27dd7d30088e690a046/image-60.jpg)
Financial Applications B 2. The expected capital gain: ECG = E[d. V] = [ XVx+0. 5 2 X 2 Vxx]dt since E[d. W] = 0 3. The Expected cash flow: ECF = X dt Zvi Wiener Cont. Time. Fin - 1 60

Financial Applications B 4. Total return: TR = ECG + ECF = [ XVx+X+0. 5 2 X 2 Vxx]dt 5. But the return must be equal to the risk free return on the same investment V. r. Vdt = [ XVx+X+0. 5 2 X 2 Vxx]dt 6. Thus the PDE: r. V = XVx+X+0. 5 2 X 2 Vxx Zvi Wiener Cont. Time. Fin - 1 61

Financial Applications B r. V = XVx+X+0. 5 2 X 2 Vxx there are several ways to solve it. One can guess that doubling X will double the price V. If V is proportional to X, then V = X, Vx= , and Vxx=0, then the equation becomes r X= X +X = 1/(r- ) V(X) = X/(r- ) Zvi Wiener Cont. Time. Fin - 1 62
 Zvi wiener
Zvi wiener Zvi tools
Zvi tools Zvi wiener
Zvi wiener Swot analysis in education example
Swot analysis in education example Zvi aronson
Zvi aronson Zvi margaliot
Zvi margaliot Zvi margaliot
Zvi margaliot Zvi aronson
Zvi aronson Zvi kedem
Zvi kedem Dr zvi margaliot
Dr zvi margaliot Zvi roth
Zvi roth Wiener schlosserbuben
Wiener schlosserbuben Cornelia brezik
Cornelia brezik Cara menghitung indeks keanekaragaman shannon wiener
Cara menghitung indeks keanekaragaman shannon wiener Dr craig wiener
Dr craig wiener Ito lemma stock price
Ito lemma stock price Wiener liste antibiotika
Wiener liste antibiotika Schema de lasswell
Schema de lasswell Wiener tafelspitz beilagen
Wiener tafelspitz beilagen Thomas kutschera
Thomas kutschera Wiener rh-hr terminology
Wiener rh-hr terminology Balladenjahr 1797
Balladenjahr 1797 Wiener becken referat
Wiener becken referat Fundación wiener cursos a distancia 2020
Fundación wiener cursos a distancia 2020 Wiener
Wiener Wiener
Wiener Wiener salon gulasch
Wiener salon gulasch Thomas wiener
Thomas wiener Normtabelle
Normtabelle Wiener anerkennungssystem
Wiener anerkennungssystem Wiener rh-hr terminology
Wiener rh-hr terminology Reputable isri scrap recycler
Reputable isri scrap recycler Modelo de wiener
Modelo de wiener Curva di rarefazione
Curva di rarefazione Beta diversity definition
Beta diversity definition Shannon wiener diversity index
Shannon wiener diversity index Wiener kreis
Wiener kreis Wiener verein bedingungen
Wiener verein bedingungen Non financial method of motivation
Non financial method of motivation Money-time relationship and equivalence
Money-time relationship and equivalence Financial engineering derivatives and risk management
Financial engineering derivatives and risk management Actuarial and financial engineering
Actuarial and financial engineering Financial engineering syllabus
Financial engineering syllabus Conceptual tools of financial engineering
Conceptual tools of financial engineering Financial engineering derivatives and risk management
Financial engineering derivatives and risk management Financial engineering derivatives and risk management
Financial engineering derivatives and risk management Computer based system engineering in software engineering
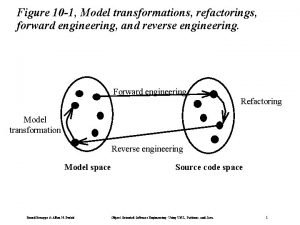
Computer based system engineering in software engineering Forward engineering and reverse engineering
Forward engineering and reverse engineering Dicapine
Dicapine Elegant systems
Elegant systems Forward and reverse engineering
Forward and reverse engineering Pshe financial literacy
Pshe financial literacy Indirect financial compensation
Indirect financial compensation Financial aid card
Financial aid card Frx report wizard
Frx report wizard Accounting subject code
Accounting subject code Why study financial market
Why study financial market What is financial social work
What is financial social work Crown money management
Crown money management Basic flow of funds through the financial system
Basic flow of funds through the financial system Dashboard laporan keuangan
Dashboard laporan keuangan Financial decision
Financial decision Equivalent annual annuity
Equivalent annual annuity