Final Master Talk Mechanising Set Theory in Coq
![The Set Theory ZF 2 [Kirst and Smolka 2017] Axioms extensionality foundation 4](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-4.jpg "The Set Theory ZF 2 [Kirst and Smolka 2017] Axioms extensionality foundation 4")
![The Hartogs Number [1915] A big ordinal 11](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-11.jpg "The Hartogs Number [1915] A big ordinal 11")
![Sierpiński‘s Theorem [1947] 12](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-12.jpg "Sierpiński‘s Theorem [1947] 12")
![Sierpiński‘s Theorem [1947] 13](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-13.jpg "Sierpiński‘s Theorem [1947] 13")
![Sierpiński‘s Theorem [1947] 14](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-14.jpg "Sierpiński‘s Theorem [1947] 14")
![Sierpiński‘s Theorem [1947] 15](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-15.jpg "Sierpiński‘s Theorem [1947] 15")
![Sierpiński‘s Theorem [1947] 16](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-16.jpg "Sierpiński‘s Theorem [1947] 16")
![Sierpiński‘s Theorem [1947] 17](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-17.jpg "Sierpiński‘s Theorem [1947] 17")
![Sierpiński‘s Theorem [1947] 18](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-18.jpg "Sierpiński‘s Theorem [1947] 18")
![Sierpiński‘s Theorem [1947] 19](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-19.jpg "Sierpiński‘s Theorem [1947] 19")
![Sierpiński‘s Theorem [1947] 20](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-20.jpg "Sierpiński‘s Theorem [1947] 20")
![Sierpiński‘s Theorem [1947] 21](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-21.jpg "Sierpiński‘s Theorem [1947] 21")
![Sierpiński‘s Theorem [1947] 22](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-22.jpg "Sierpiński‘s Theorem [1947] 22")
![Sierpiński‘s Theorem [1947] 23](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-23.jpg "Sierpiński‘s Theorem [1947] 23")
![Sierpiński‘s Theorem [1947] 24](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-24.jpg "Sierpiński‘s Theorem [1947] 24")
![Relative consistency of the axiom of choice [Gödel 1938] • 34](https://slidetodoc.com/presentation_image_h/0324b036ffdee4a832efc3981530e757/image-33.jpg "Relative consistency of the axiom of choice [Gödel 1938] • 34")
- Slides: 41
Final Master Talk Mechanising Set Theory in Coq The Generalised Continuum Hypothesis and the Axiom of Choice Felix Rech Advisor: Dominik Kirst June 26, 2020
Project Overview • 2
Global Assumptions • 3
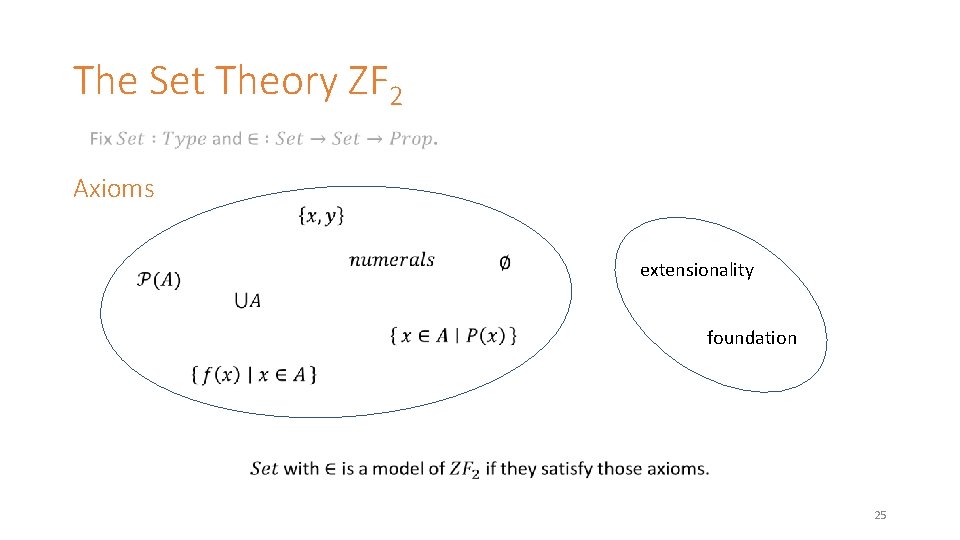
The Set Theory ZF 2 [Kirst and Smolka 2017] Axioms extensionality foundation 4
Encodings • 5
Generalised Continuum Hypothesis 6
The Axiom of Choice 7
The Well-Ordering Theorem “Every set has a well-ordering” 8
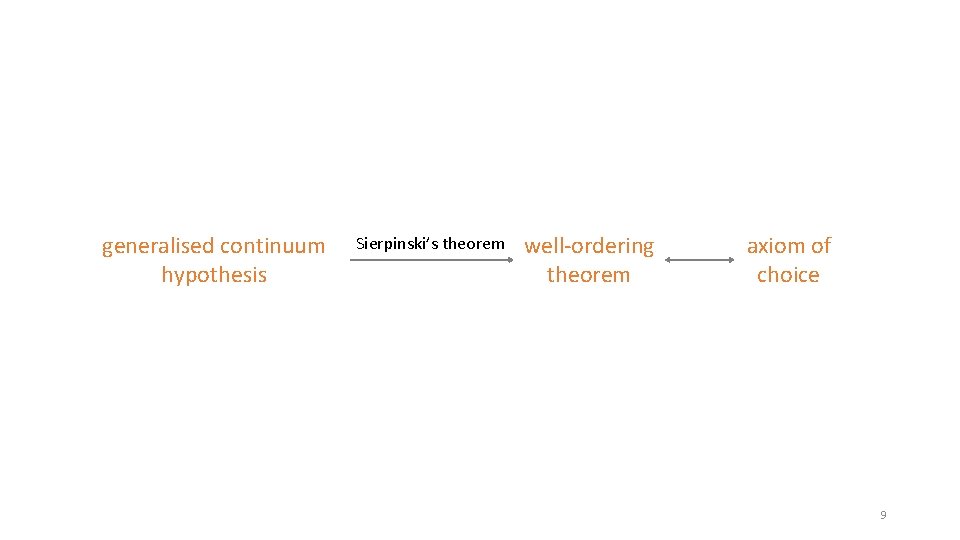
generalised continuum hypothesis Sierpinski’s theorem well-ordering theorem axiom of choice 9
Ordinals – Canonical Well-Ordered Sets Every well-ordered set has exactly one order-isomorphic ordinal. 10
The Hartogs Number [1915] A big ordinal 11
Sierpiński‘s Theorem [1947] 12
Sierpiński‘s Theorem [1947] 13
Sierpiński‘s Theorem [1947] 14
Sierpiński‘s Theorem [1947] 15
Sierpiński‘s Theorem [1947] 16
Sierpiński‘s Theorem [1947] 17
Sierpiński‘s Theorem [1947] 18
Sierpiński‘s Theorem [1947] 19
Sierpiński‘s Theorem [1947] 20
Sierpiński‘s Theorem [1947] 21
Sierpiński‘s Theorem [1947] 22
Sierpiński‘s Theorem [1947] 23
Sierpiński‘s Theorem [1947] 24
The Set Theory ZF 2 Axioms extensionality foundation 25
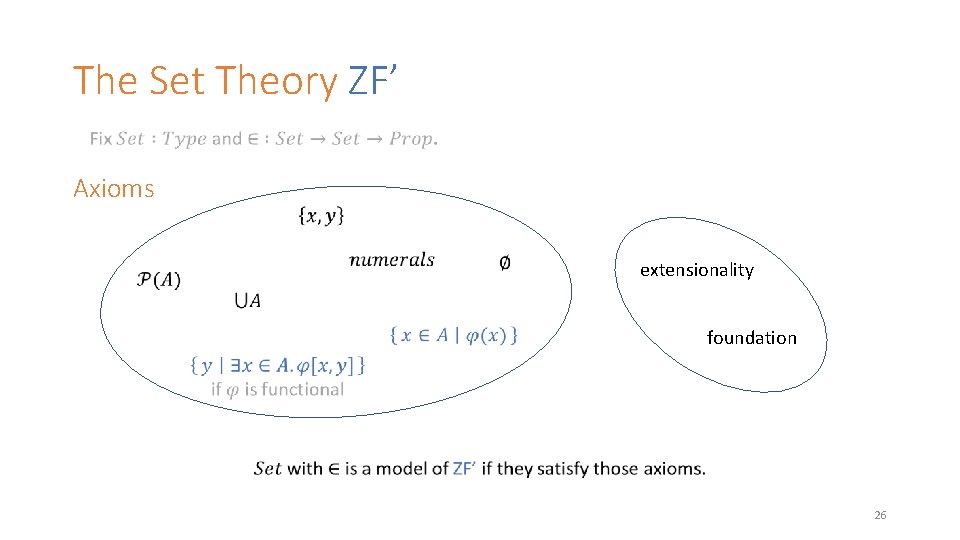
The Set Theory ZF’ Axioms extensionality foundation 26
First-Order Logic (De Bruijn notation) 27
ZF’ and First-Order ZF Given a model of ZF, the well-founded fragment is a model of ZF’. Every model of ZF’ is a model of ZF. Both are equiconsistent. 28
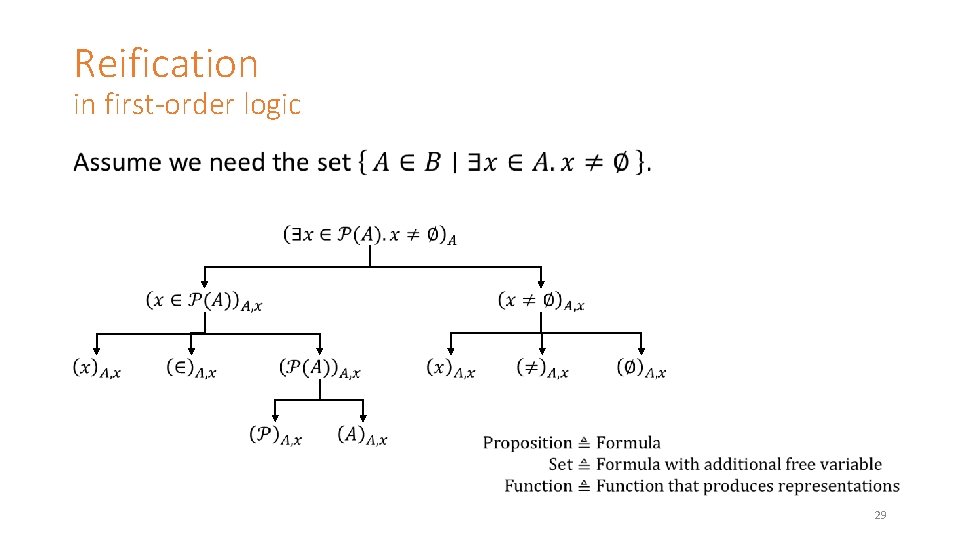
Reification in first-order logic • 29
What we can represent • 30
The Axiom of Choice (In ZF’) 32
The Well-Ordering Theorem (In ZF’) “Every set has a representable well-ordering” 33
Relative consistency of the axiom of choice [Gödel 1938] • 34
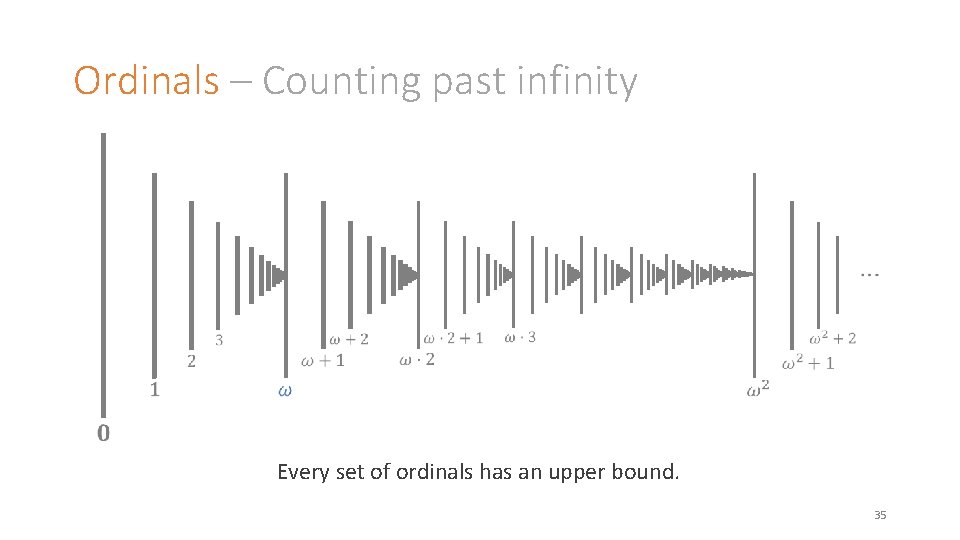
Ordinals – Counting past infinity Every set of ordinals has an upper bound. 35
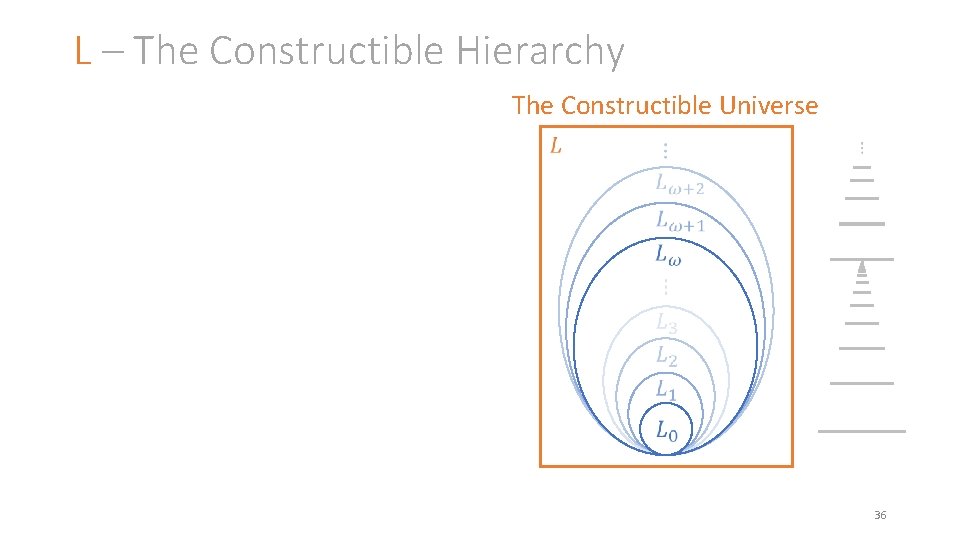
L – The Constructible Hierarchy The Constructible Universe 36
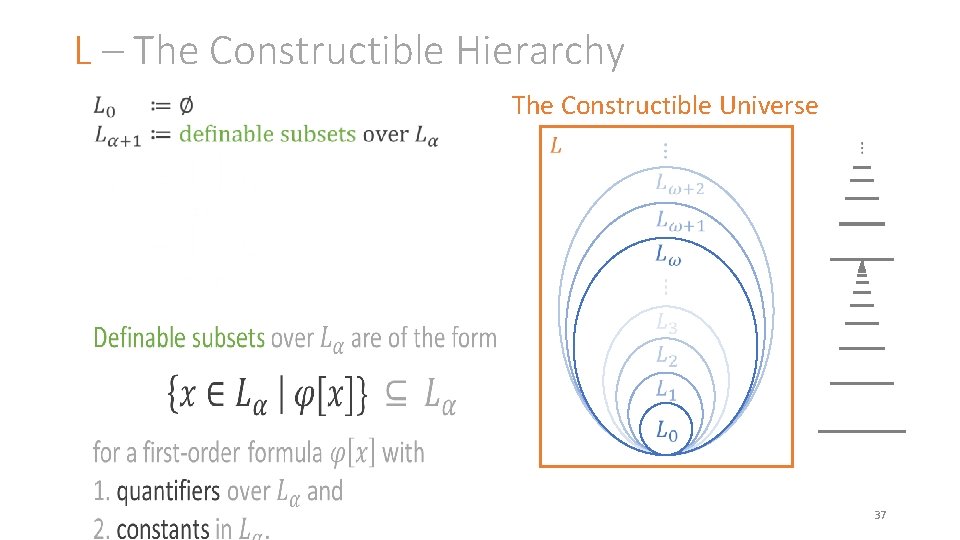
L – The Constructible Hierarchy The Constructible Universe 37
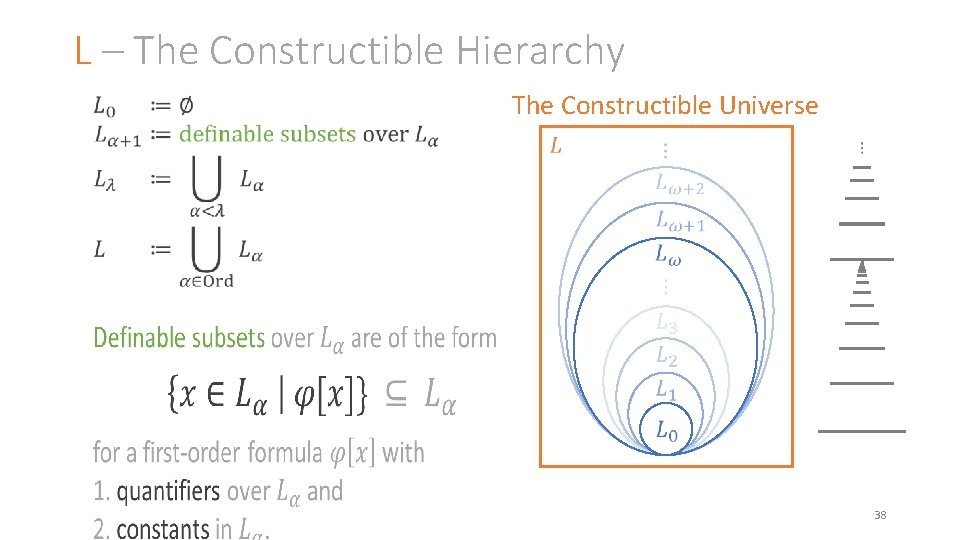
L – The Constructible Hierarchy The Constructible Universe 38
Coq Formalisation Sierpinski’s theorem 2458 lines The constructible hierarchy Incomplete Typeclasses for representations 1747 lines 39
Conclusion • ZF’ is a useful compromise between ZF 2 and first-order ZF. • Our notions of encodings and representations imitate informal practice. • Formalisation: • Sierpinski’s theorem • Consistency of the axiom of choice (incomplete) Future work • • Thank you! Consistency of the generalised continuum hypothesis Apply representations to other proofs and theories Type-theoretic version of Sierpinski’s theorem Improve representability 40
References Dominik Kirst and Gert Smolka. Categoricity results for second-order ZF in dependent type theory. International Conference on Interactive Theorem Proving. Springer, Cham, 2017. Friedrich Hartogs. Über das Problem der Wohlordnung. Mathematische Annalen 76. 4 (1915): 438 -443. Wacław Sierpiński. L'hypothèse généralisée du continu et l'axiome du choix. Fundamenta Mathematicae 1. 34 (1947): 1 -5. 41
References 2 Raymond M. Smullyan and Melvin Fitting Set Theory and the Continuum Problem Dover Publications, 2010. Kurt Gödel. The Consistency of the Axiom of Choice and of the Generalized Continuum -Hypothesis. Proceedings of the National Academy of Sciences of the United States of America vol. 24, 1938 42