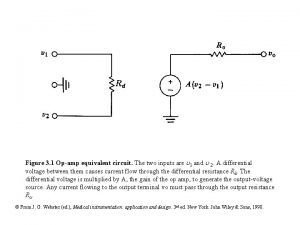
Figure 3 1 Opamp equivalent circuit The two
- Slides: 19

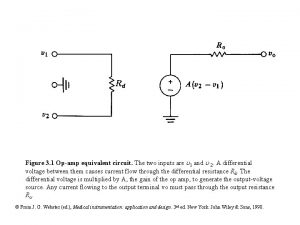
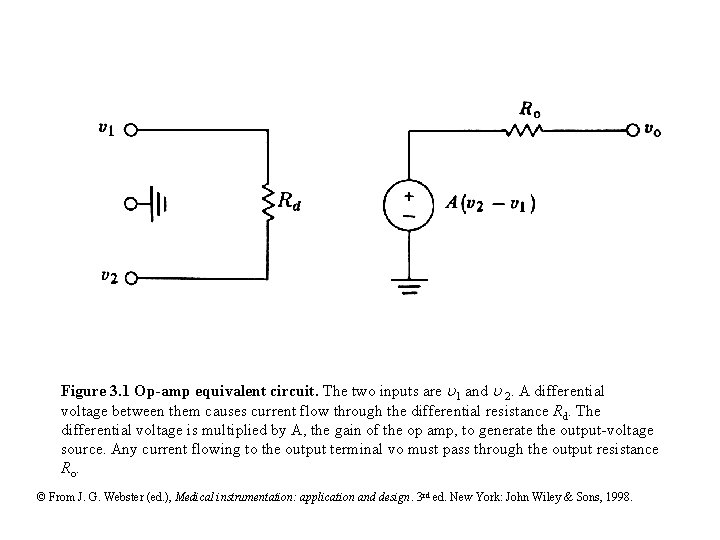
Figure 3. 1 Op-amp equivalent circuit. The two inputs are 1 and 2. A differential voltage between them causes current flow through the differential resistance Rd. The differential voltage is multiplied by A, the gain of the op amp, to generate the output-voltage source. Any current flowing to the output terminal vo must pass through the output resistance Ro. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

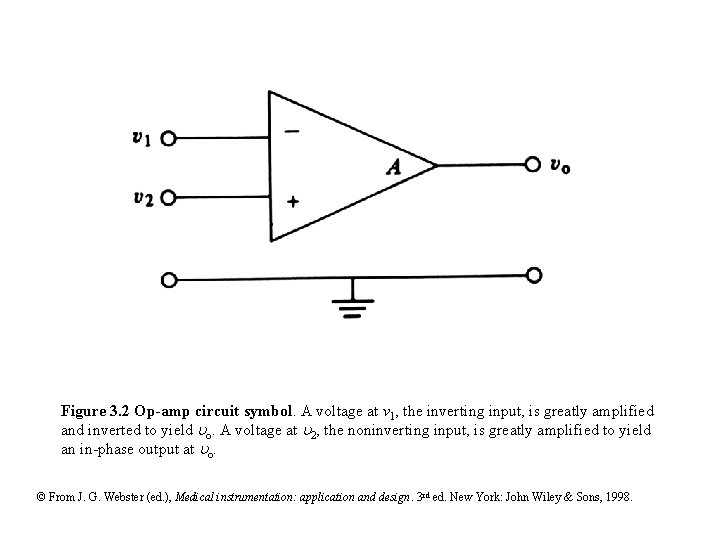
Figure 3. 2 Op-amp circuit symbol. A voltage at v 1, the inverting input, is greatly amplified and inverted to yield o. A voltage at 2, the noninverting input, is greatly amplified to yield an in-phase output at o. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

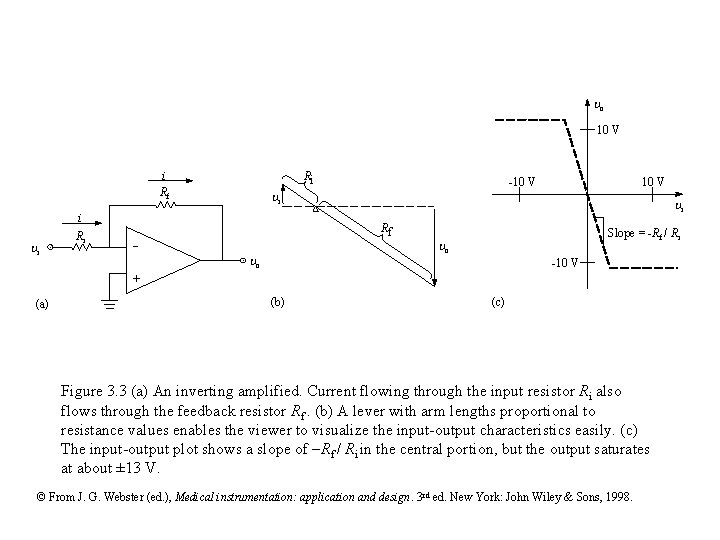
o 10 V i Rf Ri i Ri -10 V i Rf - o 10 V Slope = -Rf / Ri o -10 V + (a) (b) (c) Figure 3. 3 (a) An inverting amplified. Current flowing through the input resistor Ri also flows through the feedback resistor Rf. (b) A lever with arm lengths proportional to resistance values enables the viewer to visualize the input-output characteristics easily. (c) The input-output plot shows a slope of -Rf / Ri in the central portion, but the output saturates at about ± 13 V. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

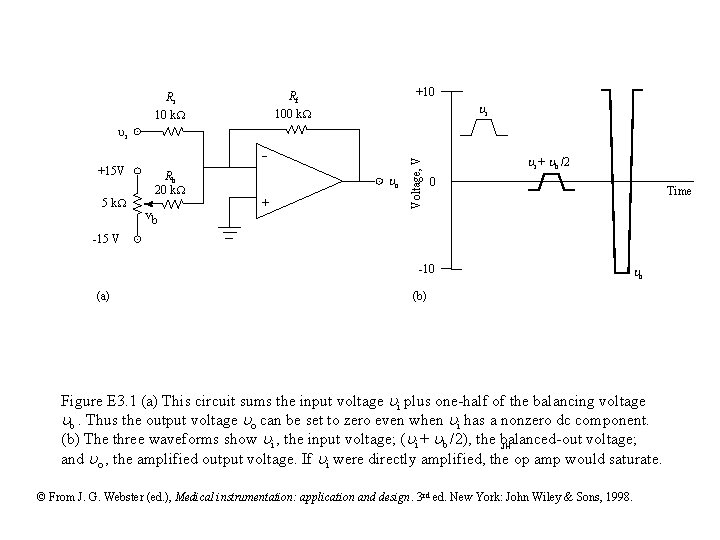
+10 Rf 100 k. W Ri 10 k. W i +15 V 5 k. W Rb 20 k. W vb o + Voltage, V i i + b /2 0 Time -15 V -10 (a) o (b) Figure E 3. 1 (a) This circuit sums the input voltage i plus one-half of the balancing voltage b. Thus the output voltage o can be set to zero even when i has a nonzero dc component. (b) The three waveforms show i , the input voltage; ( i + b /2), the balanced-out voltage; JH and o , the amplified output voltage. If i were directly amplified, the op amp would saturate. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

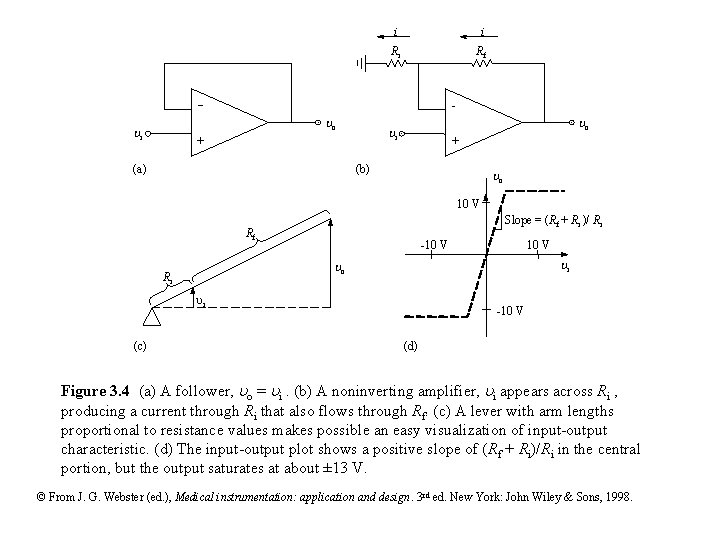
i i Ri Rf - - o i + (a) o i + (b) o 10 V Slope = (Rf + Ri )/ Ri Rf -10 V i o Ri i (c) 10 V -10 V (d) Figure 3. 4 (a) A follower, o = i. (b) A noninverting amplifier, i appears across Ri , producing a current through Ri that also flows through Rf. (c) A lever with arm lengths proportional to resistance values makes possible an easy visualization of input-output characteristic. (d) The input-output plot shows a positive slope of (Rf + Ri)/Ri in the central portion, but the output saturates at about ± 13 V. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

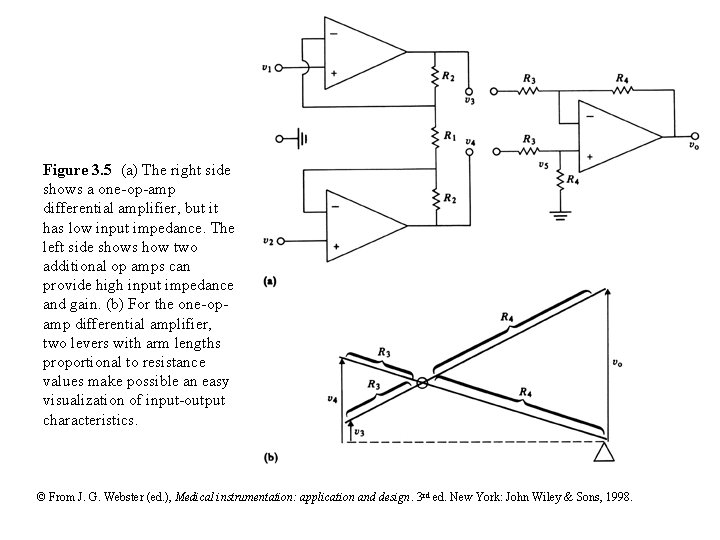
Figure 3. 5 (a) The right side shows a one-op-amp differential amplifier, but it has low input impedance. The left side shows how two additional op amps can provide high input impedance and gain. (b) For the one-opamp differential amplifier, two levers with arm lengths proportional to resistance values make possible an easy visualization of input-output characteristics. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

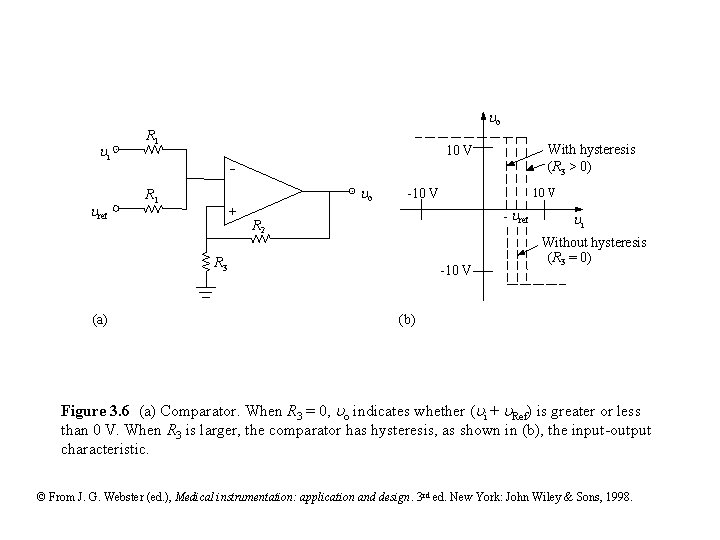
o i ref R 1 - o R 1 + -10 V - ref R 2 R 3 (a) With hysteresis (R 3 > 0) 10 V -10 V i Without hysteresis (R 3 = 0) (b) Figure 3. 6 (a) Comparator. When R 3 = 0, o indicates whether ( i + Ref) is greater or less than 0 V. When R 3 is larger, the comparator has hysteresis, as shown in (b), the input-output characteristic. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

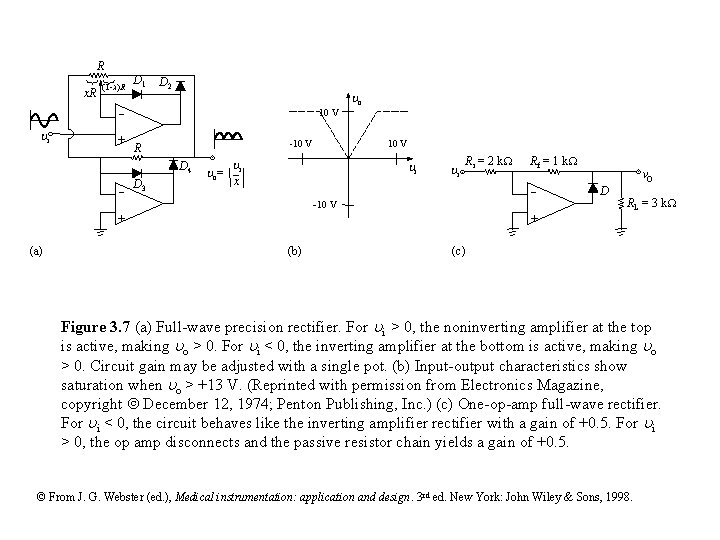
R x. R (1 -x)R D 1 D 2 o - i + 10 V -10 V R D 4 - D 3 o= 10 V i i x i Ri = 2 k. W - -10 V + (a) Rf = 1 k. W D vo RL = 3 k. W + (b) (c) Figure 3. 7 (a) Full-wave precision rectifier. For i > 0, the noninverting amplifier at the top is active, making o > 0. For i < 0, the inverting amplifier at the bottom is active, making o > 0. Circuit gain may be adjusted with a single pot. (b) Input-output characteristics show saturation when o > +13 V. (Reprinted with permission from Electronics Magazine, copyright December 12, 1974; Penton Publishing, Inc. ) (c) One-op-amp full-wave rectifier. For i < 0, the circuit behaves like the inverting amplifier rectifier with a gain of +0. 5. For i > 0, the op amp disconnects and the passive resistor chain yields a gain of +0. 5. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

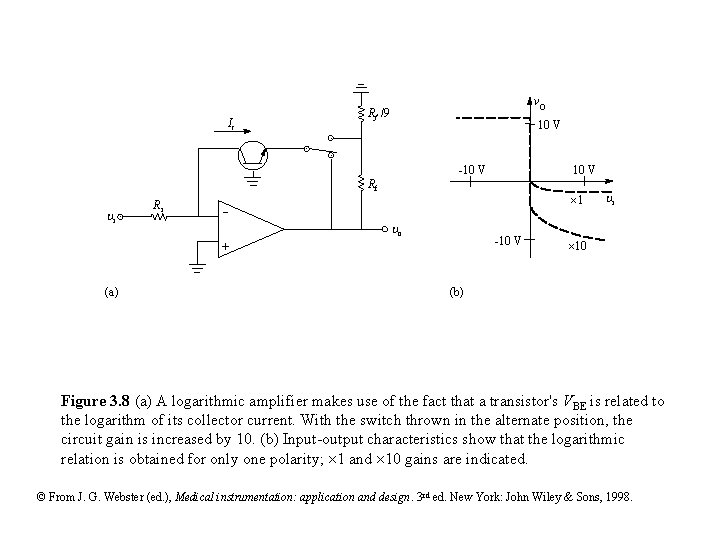
Ic vo Rf /9 10 V -10 V Rf i Ri 1 - o -10 V + (a) 10 V i 10 (b) Figure 3. 8 (a) A logarithmic amplifier makes use of the fact that a transistor's VBE is related to the logarithm of its collector current. With the switch thrown in the alternate position, the circuit gain is increased by 10. (b) Input-output characteristics show that the logarithmic relation is obtained for only one polarity; 1 and 10 gains are indicated. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

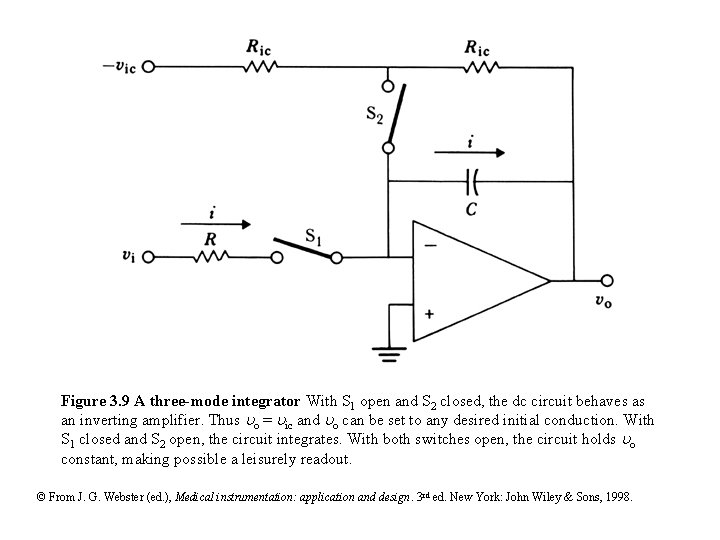
Figure 3. 9 A three-mode integrator With S 1 open and S 2 closed, the dc circuit behaves as an inverting amplifier. Thus o = ic and o can be set to any desired initial conduction. With S 1 closed and S 2 open, the circuit integrates. With both switches open, the circuit holds o constant, making possible a leisurely readout. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

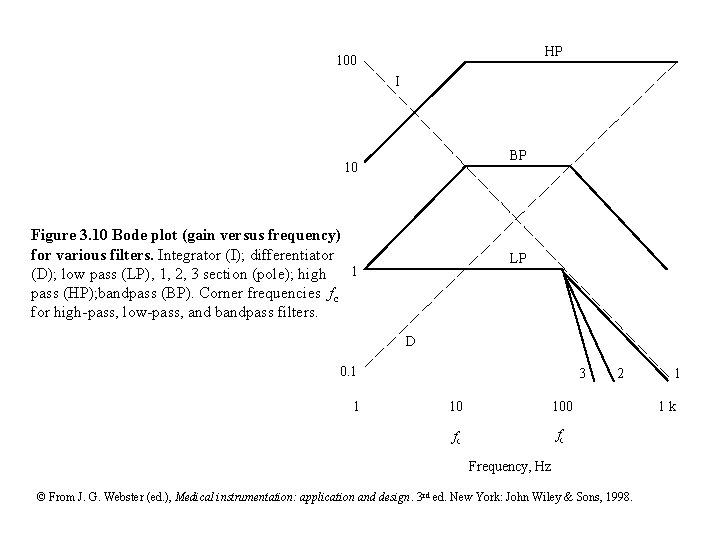
HP 100 I BP 10 Figure 3. 10 Bode plot (gain versus frequency) for various filters. Integrator (I); differentiator 1 (D); low pass (LP), 1, 2, 3 section (pole); high pass (HP); bandpass (BP). Corner frequencies fc for high-pass, low-pass, and bandpass filters. LP D 0. 1 1 3 10 100 fc fc 2 Frequency, Hz © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998. 1 1 k

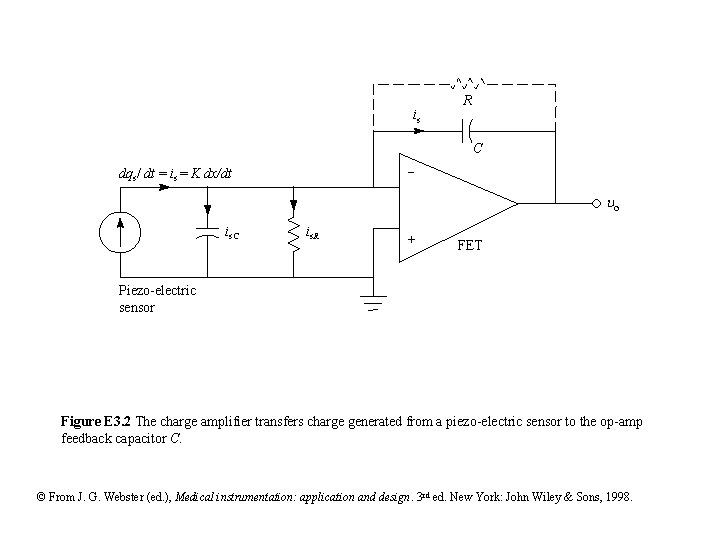
is R C - dqs/ dt = is = K dx/dt o is. C is. R + FET Piezo-electric sensor Figure E 3. 2 The charge amplifier transfers charge generated from a piezo-electric sensor to the op-amp feedback capacitor C. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

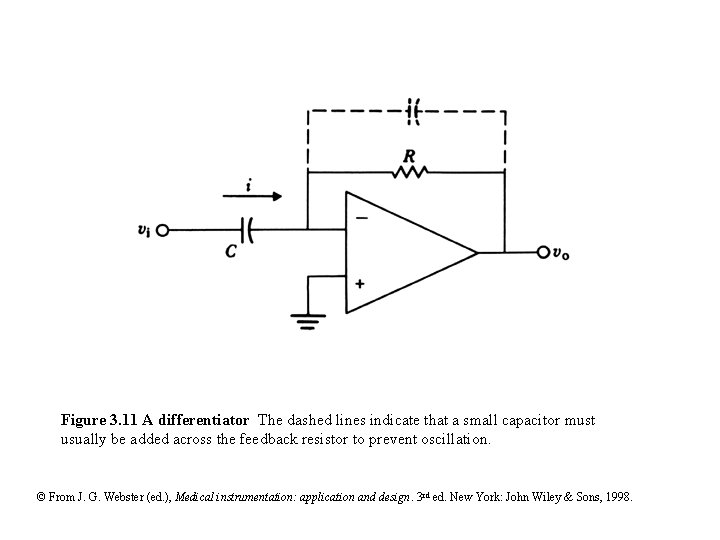
Figure 3. 11 A differentiator The dashed lines indicate that a small capacitor must usually be added across the feedback resistor to prevent oscillation. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

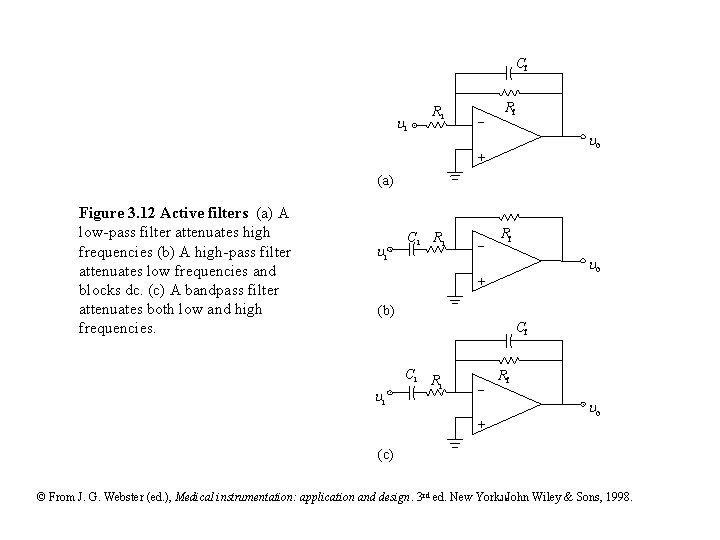
Cf i Ri - Rf o + (a) Figure 3. 12 Active filters (a) A low-pass filter attenuates high frequencies (b) A high-pass filter attenuates low frequencies and blocks dc. (c) A bandpass filter attenuates both low and high frequencies. i Ci Ri - Rf o + (b) Cf i Ci R i + Rf o (c) © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: JHJohn Wiley & Sons, 1998.

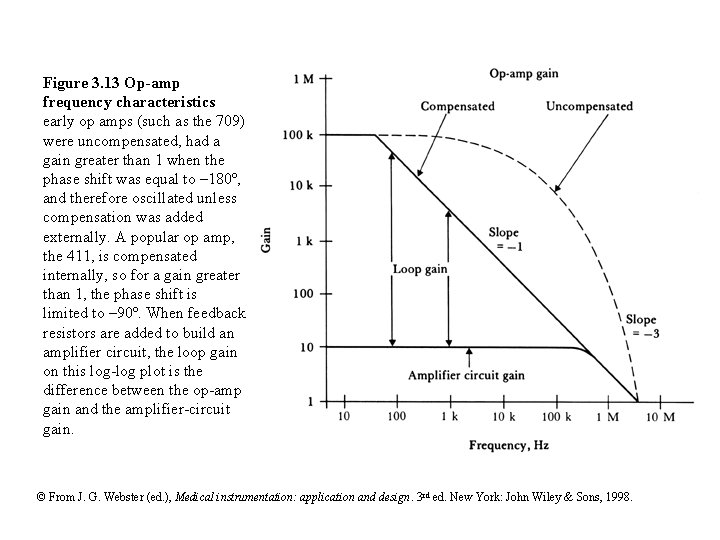
Figure 3. 13 Op-amp frequency characteristics early op amps (such as the 709) were uncompensated, had a gain greater than 1 when the phase shift was equal to – 180º, and therefore oscillated unless compensation was added externally. A popular op amp, the 411, is compensated internally, so for a gain greater than 1, the phase shift is limited to – 90º. When feedback resistors are added to build an amplifier circuit, the loop gain on this log-log plot is the difference between the op-amp gain and the amplifier-circuit gain. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

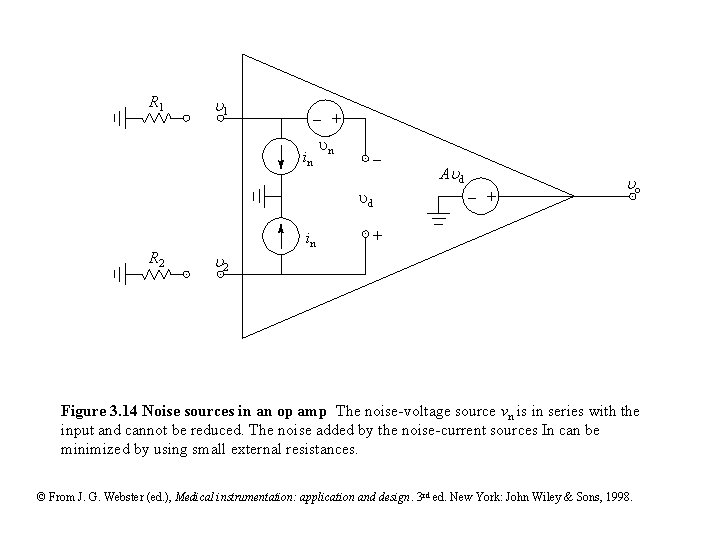
R 1 1 - + in n d R 2 in A d - + o + 2 Figure 3. 14 Noise sources in an op amp The noise-voltage source vn is in series with the input and cannot be reduced. The noise added by the noise-current sources In can be minimized by using small external resistances. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

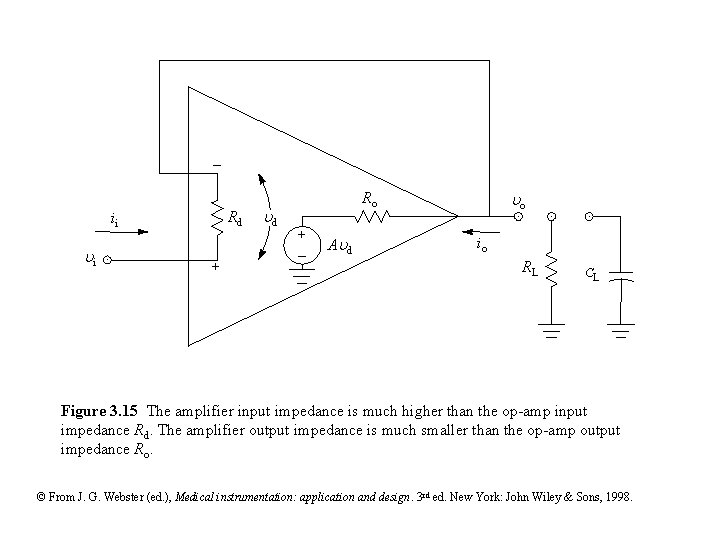
Rd ii i + d o Ro + - A d io RL CL Figure 3. 15 The amplifier input impedance is much higher than the op-amp input impedance Rd. The amplifier output impedance is much smaller than the op-amp output impedance Ro. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

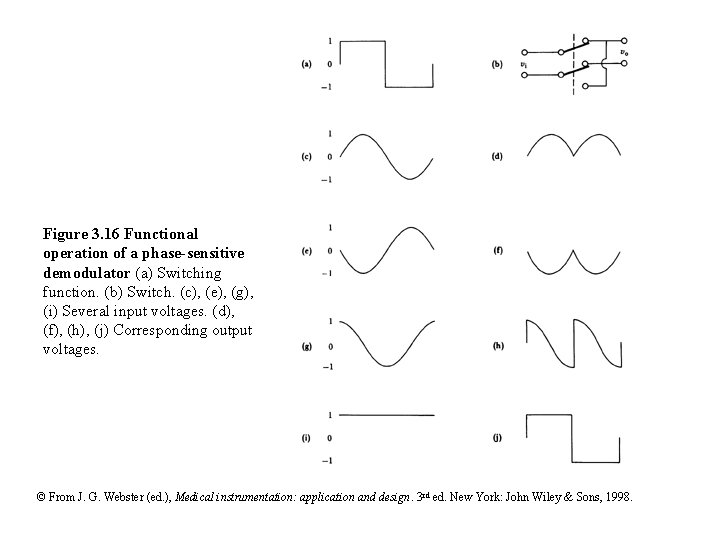
Figure 3. 16 Functional operation of a phase-sensitive demodulator (a) Switching function. (b) Switch. (c), (e), (g), (i) Several input voltages. (d), (f), (h), (j) Corresponding output voltages. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.

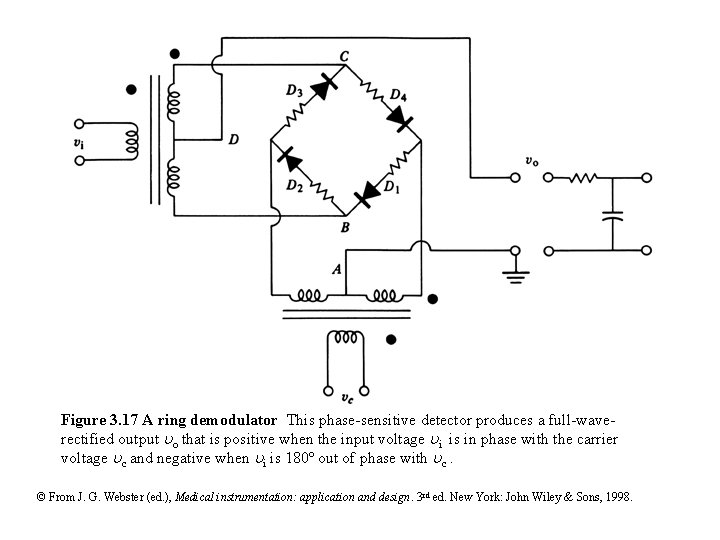
Figure 3. 17 A ring demodulator This phase-sensitive detector produces a full-waverectified output o that is positive when the input voltage i is in phase with the carrier voltage c and negative when i is 180º out of phase with c. © From J. G. Webster (ed. ), Medical instrumentation: application and design. 3 rd ed. New York: John Wiley & Sons, 1998.
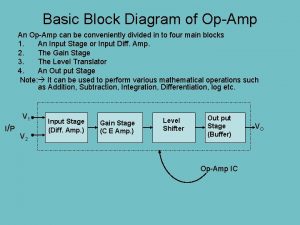
 Opamp equivalent circuit
Opamp equivalent circuit Difference between ideal and practical op amp
Difference between ideal and practical op amp Op amp sembolü
Op amp sembolü Opamp
Opamp Contoh soal op amp inverting
Contoh soal op amp inverting Applications of amplifier
Applications of amplifier çarpmada integral alma
çarpmada integral alma Ideal opamp
Ideal opamp Gerilim izleyici
Gerilim izleyici Operational amplifier exercises
Operational amplifier exercises Virtual ground in opamp
Virtual ground in opamp Parts of 3 phase induction motor
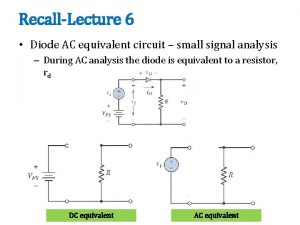
Parts of 3 phase induction motor Small signal equivalent circuit
Small signal equivalent circuit How to find req in a series circuit
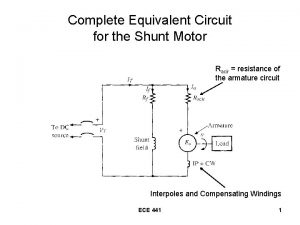
How to find req in a series circuit Dc shunt motor equivalent circuit
Dc shunt motor equivalent circuit Transistor circuit analysis
Transistor circuit analysis Equivalent resistance of a parallel circuit
Equivalent resistance of a parallel circuit Laplace transform circuits
Laplace transform circuits 1/gm mosfet
1/gm mosfet Equivalent circuit of zener diode
Equivalent circuit of zener diode