Sequential Circuit Design State Optimization Equivalent States Two

Sequential Circuit Design

State Optimization • Equivalent States: Ø Two states are equivalent if, for each member of the set of inputs, Ø they give exactly the same output and Ø send the circuit either to the same state or to an equivalent state. Ø If two states are equivalent, one can be eliminated without effecting the behavior of the FSM. 2

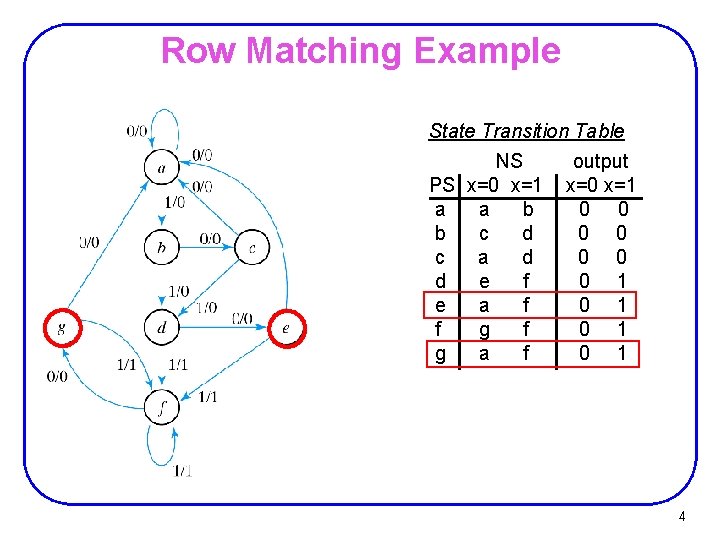
Row Matching Example State Transition Table NS PS x=0 x=1 a a b b c d c a d d e f e a f f g a f output x=0 x=1 0 0 0 0 1 0 1 4

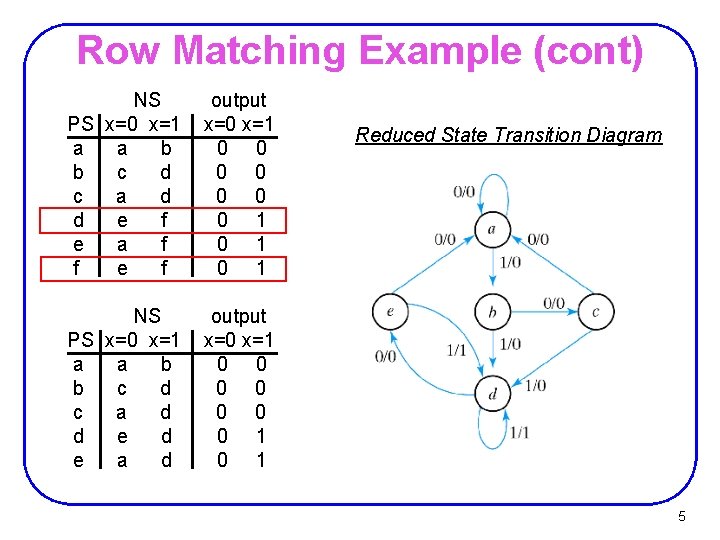
Row Matching Example (cont) NS PS x=0 x=1 a a b b c d c a d d e f e a f f e f output x=0 x=1 0 0 0 0 1 0 1 NS PS x=0 x=1 a a b b c d c a d d e a d output x=0 x=1 0 0 0 0 1 Reduced State Transition Diagram 5

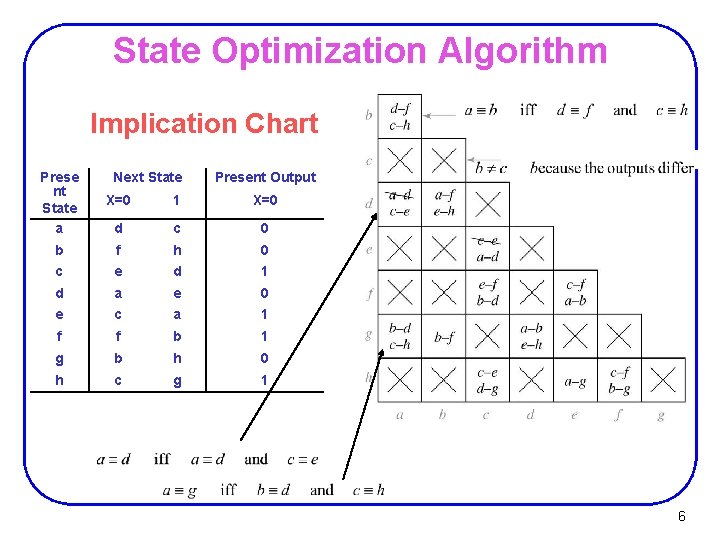
State Optimization Algorithm Implication Chart Prese nt State a Next State Present Output X=0 1 X=0 d c 0 b f h 0 c e d 1 d a e 0 e c a 1 f f b 1 g b h 0 h c g 1 6

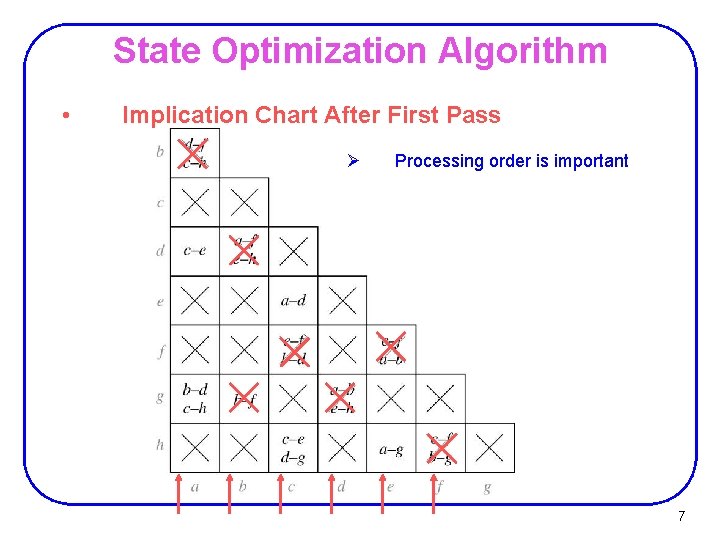
State Optimization Algorithm • Implication Chart After First Pass Ø Processing order is important 7

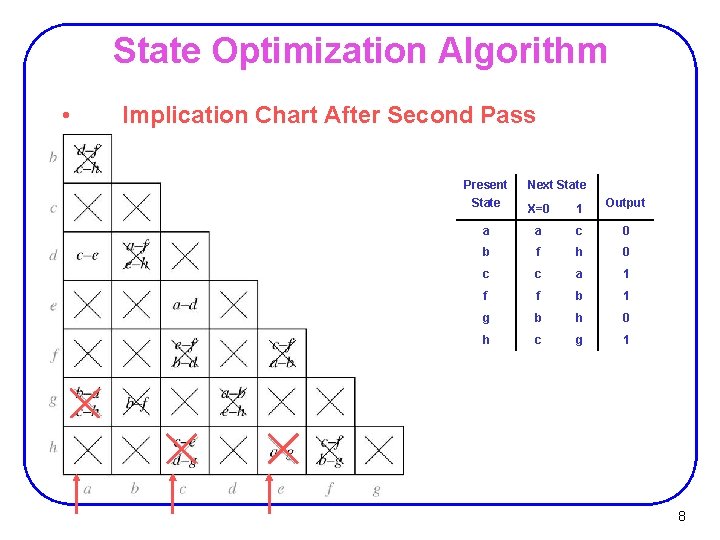
State Optimization Algorithm • Implication Chart After Second Pass Present State Next State Output X=0 1 a a c 0 b f h 0 c c a 1 f f b 1 g b h 0 h c g 1 8

Equivalent Sequential Circuits • Definition: Ø Sequential circuit N 1 is equivalent to sequential circuit N 2 if Ø for each state p in N 1, there is a state q in N 2 such that p≡q , and Ø conversely, for each state s in N 2 , there is a state t in N 1 such that s≡t. 9

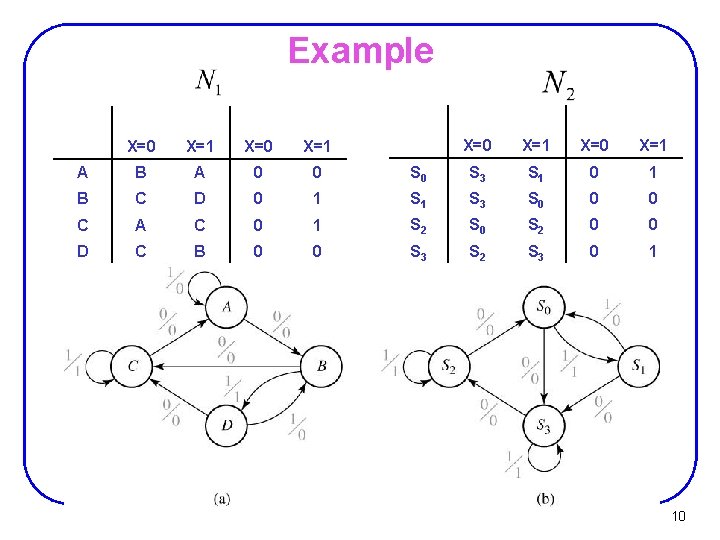
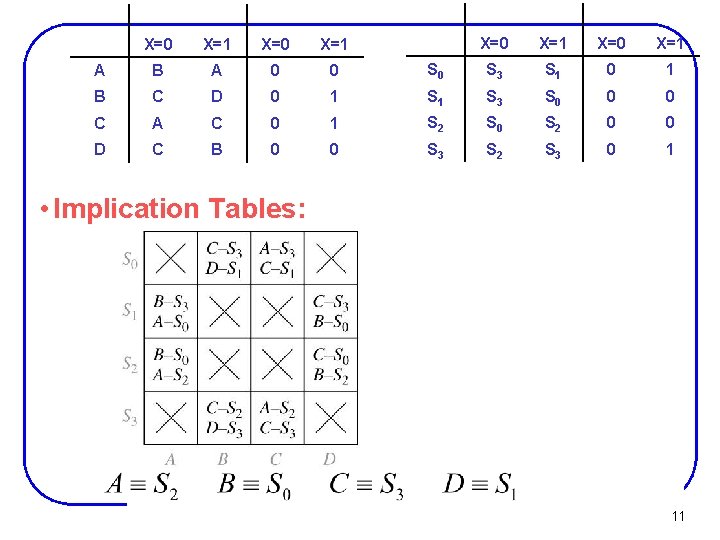
Example X=0 X=1 S 0 S 3 S 1 0 1 1 S 3 S 0 0 1 S 2 S 0 S 2 0 0 S 3 S 2 S 3 0 1 X=0 X=1 A B A 0 0 B C D 0 C A C D C B 10

X=0 X=1 S 0 S 3 S 1 0 1 1 S 3 S 0 0 1 S 2 S 0 S 2 0 0 S 3 S 2 S 3 0 1 X=0 X=1 A B A 0 0 B C D 0 C A C D C B • Implication Tables: 11

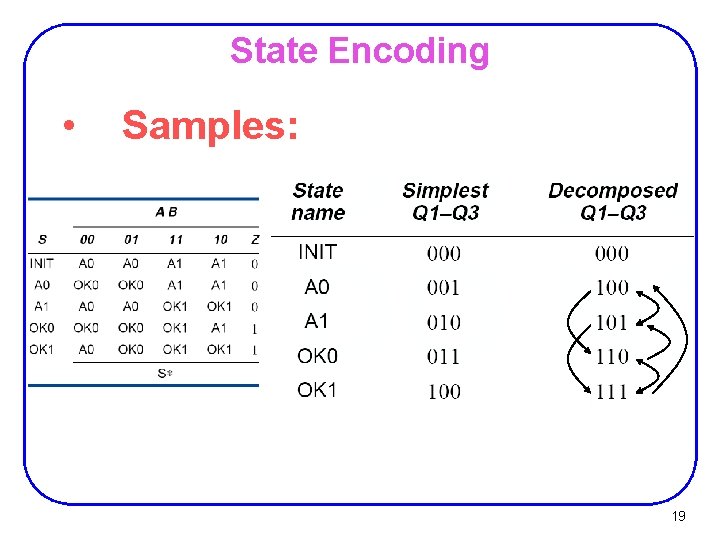
State Encoding Ø The simplest assignment of s coded states to 2 n possible states is to use the first s binary integers in binary counting order. Ø Ø However, the simplest state assignment does not always lead to the simplest circuit. Ø Ø 000, 001, 010, 011, 100 In fact, the state assignment often has a major effect on circuit cost (was previously shown). In general, the only formal way to find the best assignment is to try all the assignments. Ø That’s too much work!! 12

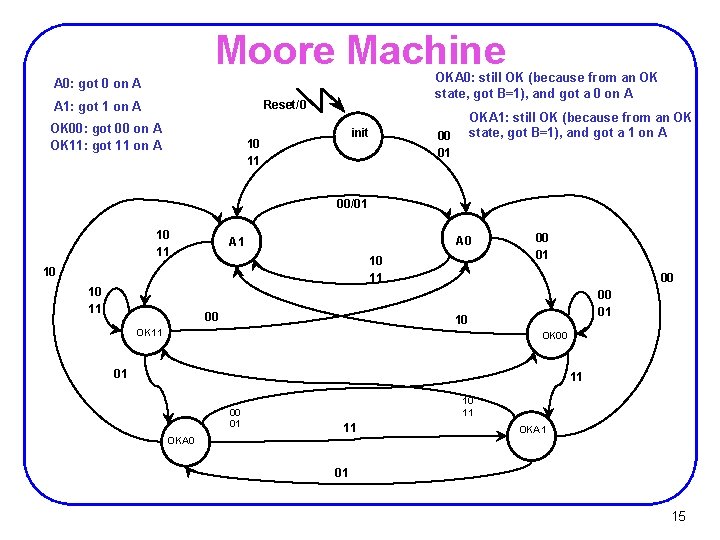
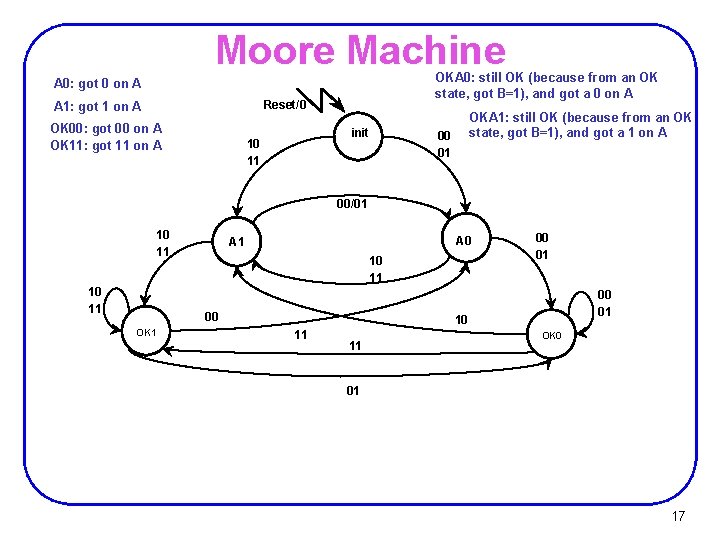
Moore Machine OKA 0: still OK (because from an OK state, got B=1), and got a 0 on A A 0: got 0 on A Reset/0 A 1: got 1 on A OK 00: got 00 on A OK 11: got 11 on A init 10 11 OKA 1: still OK (because from an OK state, got B=1), and got a 1 on A 00 01 00/01 10 11 A 0 A 1 10 10 11 00 00 01 10 OK 11 OK 00 01 11 00 01 10 11 11 OKA 0 01 15

State Table Ø Ø OK 00 and OKA 0 are equivalent OK 11 and OKA 1 are equivalent 16

Moore Machine OKA 0: still OK (because from an OK state, got B=1), and got a 0 on A A 0: got 0 on A Reset/0 A 1: got 1 on A OK 00: got 00 on A OK 11: got 11 on A init 10 11 OKA 1: still OK (because from an OK state, got B=1), and got a 1 on A 00 01 00/01 10 11 A 0 A 1 10 11 00 OK 1 00 01 10 11 11 OK 0 01 17

State Encoding • Guidelines: Ø Choose an initial coded state into which the machine can easily be forced at reset Ø 00. . . 00 or 11. . . 11 in typical circuits. Ø Minimize the number of state variables that change on each transition. Ø Maximize the number of state variables that don’t change in a group of related states Ø i. e. , a group of states in which most of transitions stay in the group. 18

State Encoding • Samples: 19

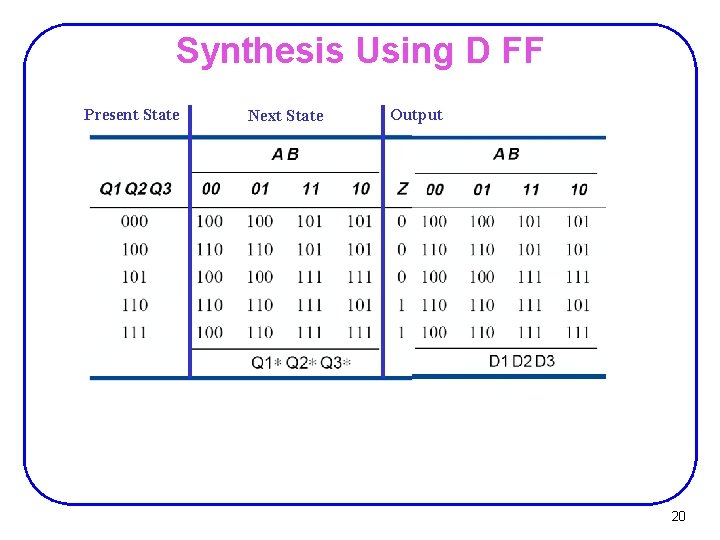
Synthesis Using D FF Present State Next State Output 20

State Assignment • Unused States: Ø Each of the m states must be assigned a unique code Ø Minimum number of bits required is n such that n ≥ log 2 m where x is the smallest integer ≥ x Ø There are 2 n - m unused states 21

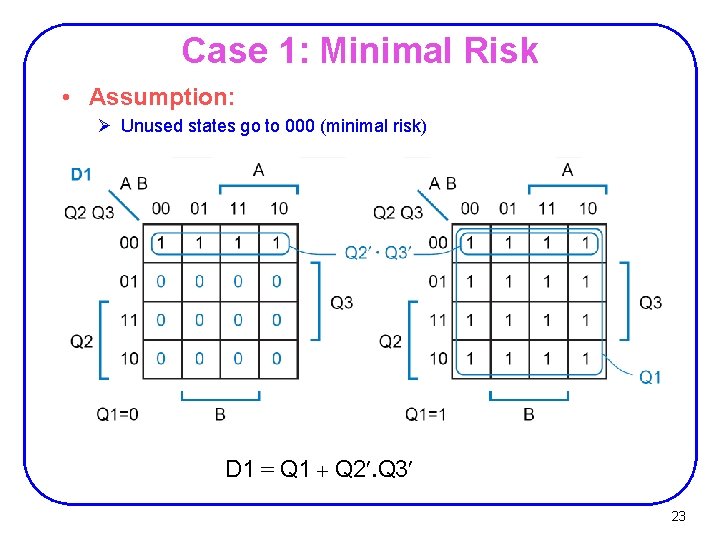
State Assignment • Unused States: Ø Minimal risk: Ø Assumes that it is possible for the state machine somehow to get into one of the unused (or “illegal”) states, Ø Ø Ø (due to a hardware failure, an unexpected input). Therefore, all of the unused state-variable combinations are identified, and explicit next-state entries are made so that, for any input combination, the unused states go to the “initial” state Minimal cost: Ø Ø Assumes that the machine will never enter an unused state. Therefore, in the transition and excitation tables, the next-state entries of the unused states can be marked as “don’t-cares”. 22

Case 1: Minimal Risk • Assumption: Ø Unused states go to 000 (minimal risk) D 1 = Q 1 + Q 2¢. Q 3¢ 23

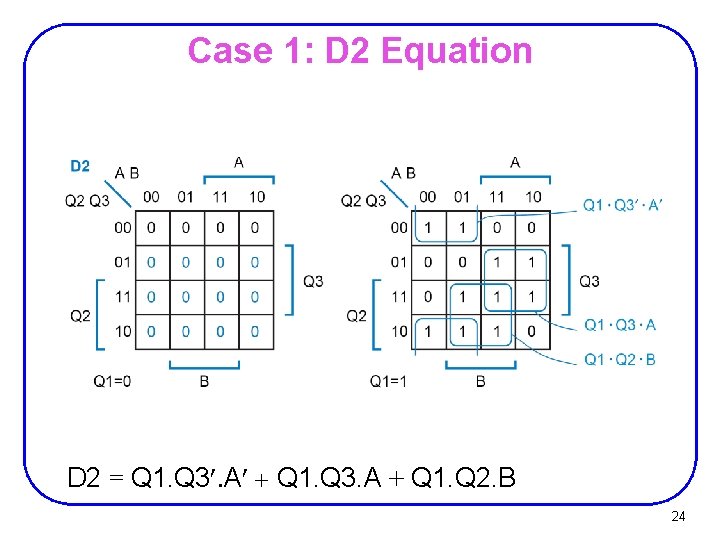
Case 1: D 2 Equation D 2 = Q 1. Q 3¢. A¢ + Q 1. Q 3. A + Q 1. Q 2. B 24

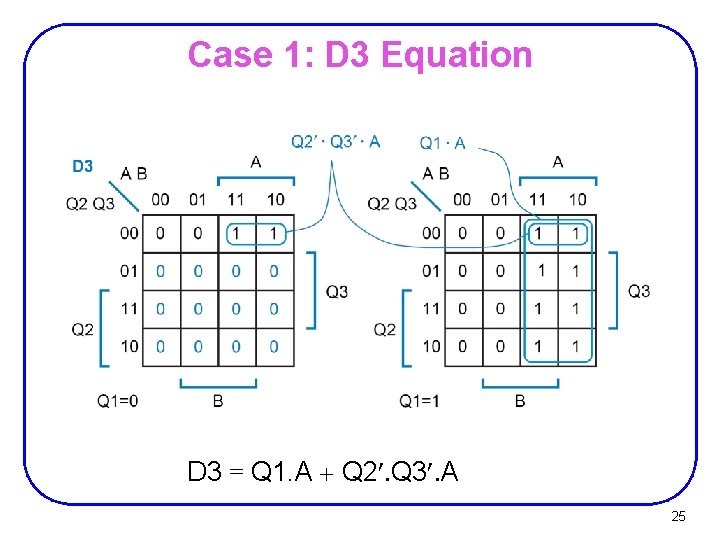
Case 1: D 3 Equation D 3 = Q 1. A + Q 2¢. Q 3¢. A 25

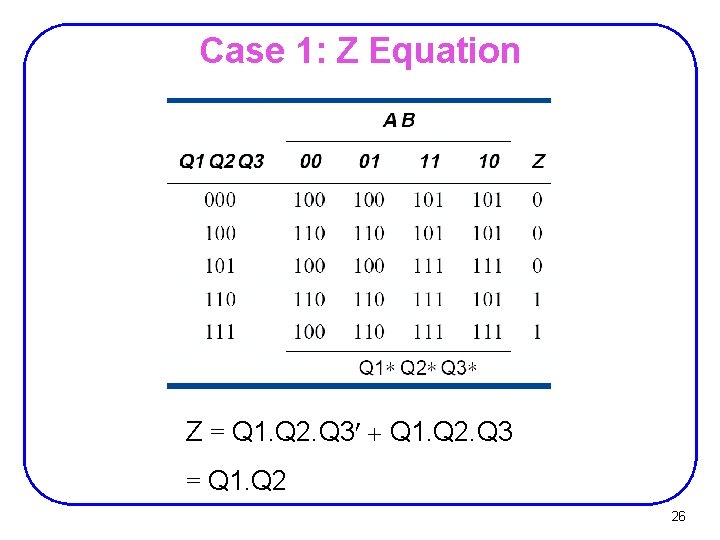
Case 1: Z Equation Z = Q 1. Q 2. Q 3¢ + Q 1. Q 2. Q 3 = Q 1. Q 2 26

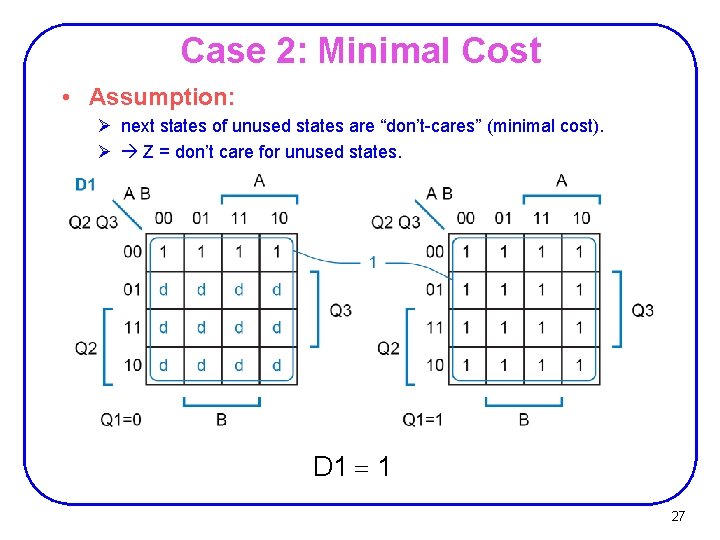
Case 2: Minimal Cost • Assumption: Ø next states of unused states are “don’t-cares” (minimal cost). Ø Z = don’t care for unused states. D 1 = 1 27

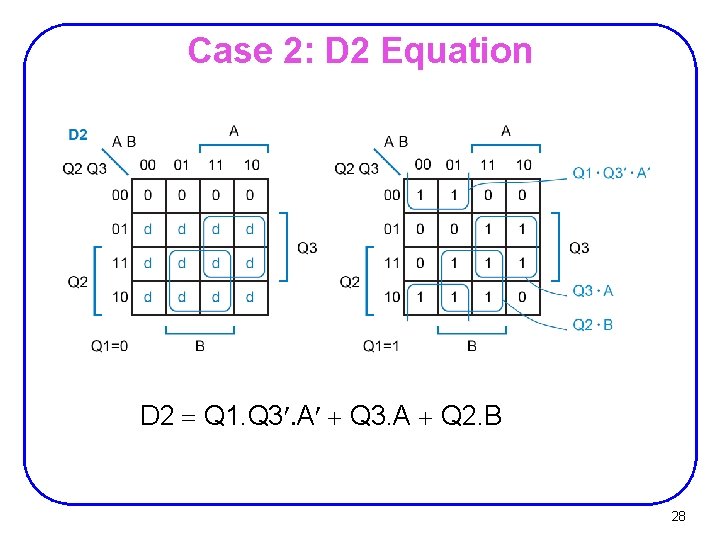
Case 2: D 2 Equation D 2 = Q 1. Q 3¢. A¢ + Q 3. A + Q 2. B 28

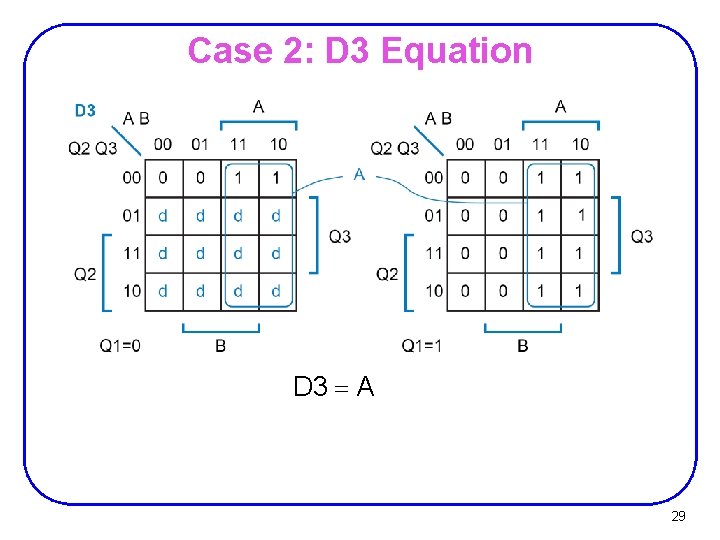
Case 2: D 3 Equation D 3 = A 29

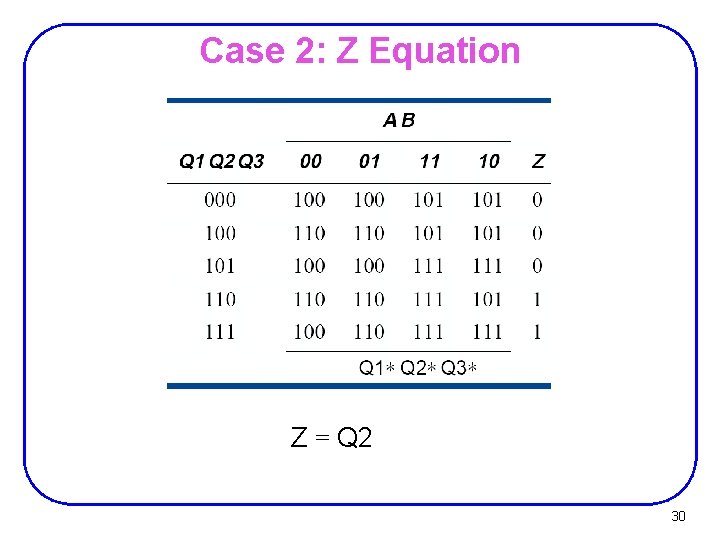
Case 2: Z Equation Z = Q 2 30

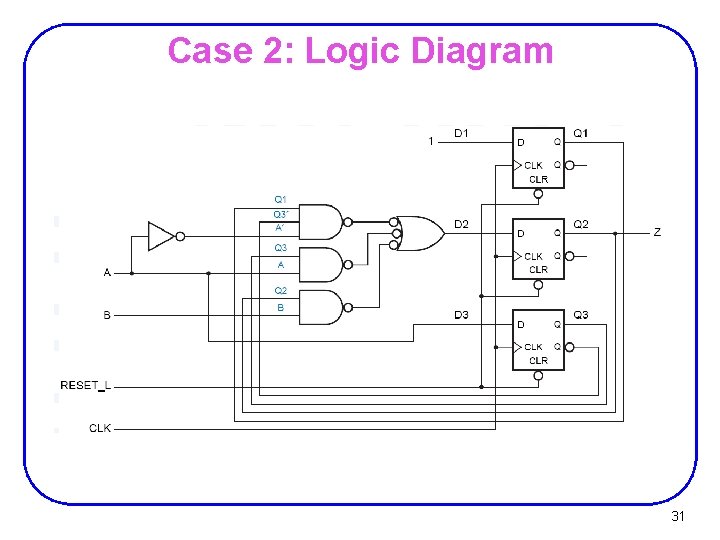
Case 2: Logic Diagram 31