Expected accuracy sequence alignment Usman Roshan Optimal pairwise

Expected accuracy sequence alignment Usman Roshan

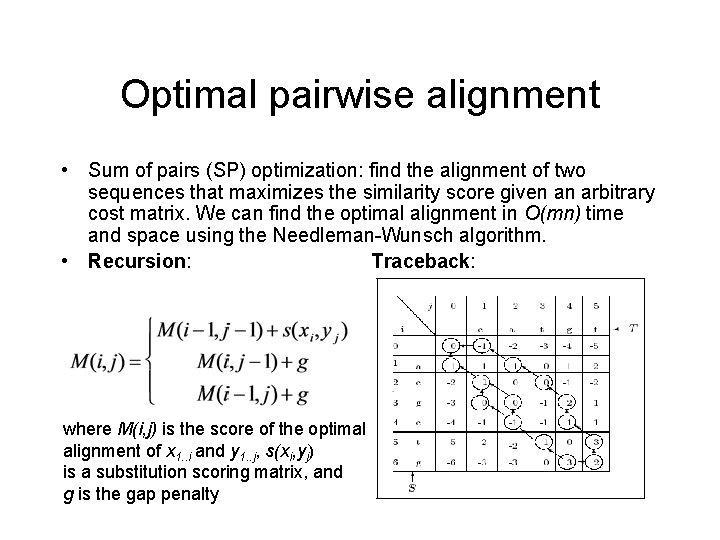
Optimal pairwise alignment • Sum of pairs (SP) optimization: find the alignment of two sequences that maximizes the similarity score given an arbitrary cost matrix. We can find the optimal alignment in O(mn) time and space using the Needleman-Wunsch algorithm. • Recursion: Traceback: where M(i, j) is the score of the optimal alignment of x 1. . i and y 1. . j, s(xi, yj) is a substitution scoring matrix, and g is the gap penalty

Affine gap penalties • Affine gap model allows for long insertions in distant proteins by charging a lower penalty for extension gaps. We define g as the gap open penalty (first gap) and e as the gap extension penalty (additional gaps) • Alignment: – ACACCCT – AC-CT-T – Score = 0 ACACCCC AC--CTT Score = 0. 9 • Trivial cost matrix: match=+1, mismatch=0, gapopen= -2, gapextension=-0. 1

Affine penalty recursion M(i, j) denotes alignments of x 1. . i and y 1. . j ending with a match/mismatch. E(i, j) denotes alignments of x 1. . i and y 1. . j such that yj is paired with a gap. F(i, j) defined similarly. Recursion takes O(mn) time where m and n are lengths of x and y respectively.

Expected accuracy alignment • The dynamic programming formulation allows us to find the optimal alignment defined by a scoring matrix and gap penalties. This may not necessarily be the most “accurate” or biologically informative. • We now look at a different formulation of alignment that allows us to compute the most accurate one instead of the optimal one.

Posterior probability of xi aligned to yj • Let A be the set of all alignments of sequences x and y, and define P(a|x, y) to be the probability that alignment a (of x and y) is the true alignment a*. • We define the posterior probability of the ith residue of x (xi) aligning to the jth residue of y (yj) in the true alignment (a*) of x and y as Do et. al. , Genome Research, 2005

Expected accuracy of alignment • We can define the expected accuracy of an alignment a as Do et. al. , Genome Research, 2005 • The maximum expected accuracy alignment can be obtained by the same dynamic programming algorithm

Example for expected accuracy • • True alignment AC_CG ACCCA Expected accuracy=(1+1+0+1+1)/4=1 • • Estimated alignment ACC_G ACCCA Expected accuracy=(1+1+0. 1+0+1)/4 ~ 0. 75

Estimating posterior probabilities • If correct posterior probabilities can be computed then we can compute the correct alignment. Now it remains to estimate these probabilities from the data • PROBCONS (Do et. al. , Genome Research 2006): estimate probabilities from pairwise HMMs using forward and backward recursions (as defined in Durbin et. al. 1998) • Probalign (Roshan and Livesay, Bioinformatics 2006): estimate probabilities using partition function dynamic programming matrices

HMM posterior probabilities • Consider the probability of all alignments of sequences X and Y under a given HMM. • Let M(i, j) be the sum of the probabilities of all alignments of X 1. . . i and Y 1…j that end in match or mismatch. • Then M(i, j) is given by • We calculate X(i, j) and Y(i, j) in the same way. • We call these forward probabilities: – f(i, j) = M(i, j)+X(i, j)+Y(i, j)

HMM posterior probabilities • Similarly we can calculate backward probabilties M’(i, j). • Define M’(i, j) as the sum of probabilities of all alignments of Xi. . m and Yj. . n such that Xi and Yj are aligned to each other. • The indices i and j start from m and n respectively and decrease • These are also called backward probabilities. – B(i, j)=M’(i, j)+X’(i, j)+Y’(i, j)

HMM posterior probabilities • The posterior probability of xi aligned to yj is given by

Partition function posterior probabilities • Standard alignment score: • Probability of alignment (Miyazawa, Prot. Eng. 1995) • If we knew the alignment partition function then

Partition function posterior probabilities • Alignment partition function (Miyazawa, Prot. Eng. 1995) • Subsequently

Partition function posterior probabilities • More generally the forward partition function matrices are calculated as

Partition function matrices vs. standard affine recursions

Posterior probability calculation • If we defined Z’ as the “backward” partition function matrices then

Posterior probabilities using alignment ensembles • By generating an ensemble A(n, x, y) of n alignments of x and y we can estimate P(xi~yj) by counting the number of times xi is aligned to yj. . Note that this means we are assigning equal weights to all alignments in the ensemble.

Generating ensemble of alignments • We can use stochastic backtracking (Muckstein et. al. , Bioinformatics, 2002) to generate a given number of optimal and suboptimal alignments. • At every step in the traceback we assign a probability to each of the three possible positions. • This allows us to “sample” alignments from their partition function probability distribution. • Posteror probabilities turn out to be the same when calculated using forward and backward partition function matrices.

Probalign 1. For each pair of sequences (x, y) in the input set – a. Compute partition function matrices Z(T) – b. Estimate posterior probability matrix P(xi ~ yj) for (x, y) by • Perform the probabilistic consistency transformation and compute a maximal expected accuracy multiple alignment: align sequence profiles along a guide-tree and follow by iterative refinement (Do et. al. ).

Experimental results • http: //bioinformatics. oxfordjournals. org/c ontent/26/16/1958