Evolutionary Game Dynamics Classic Game Theory Selfish players



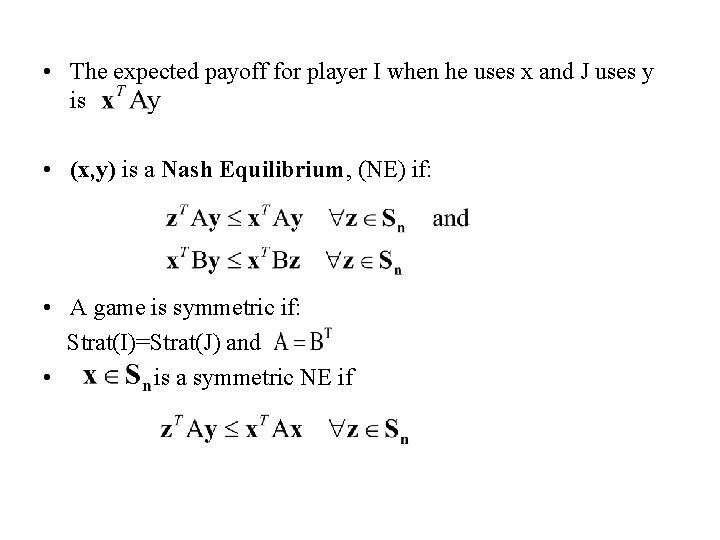

































- Slides: 42

Evolutionary Game Dynamics

• Classic Game Theory: Selfish players are involved in a game and each of them has to decide between different strategies in order to maximize a payoff, which depends on the strategies of all players • Evolutionary game theory: Entire groups of players are involved in a game. Each group is programmed to use some strategy. Strategies with high payoff, fitness, spread through the overall population. The payoff of a player depends on the strategies of the rest of the players and hence on the frequency of each strategy within the overall population. This yields a feedback loop whose dynamics is the object of evolutionary game theory

Game Theory Background Consider a game with: • Two players I, J • Strategy spaces • Payoff matrices A, B nxm. (resp. ) denotes the payoff of player I (resp. J) when I uses Strat(I) and J uses Strat(J) • Mixed strategy: the probability of player I using the probability of player J using Player I Player J
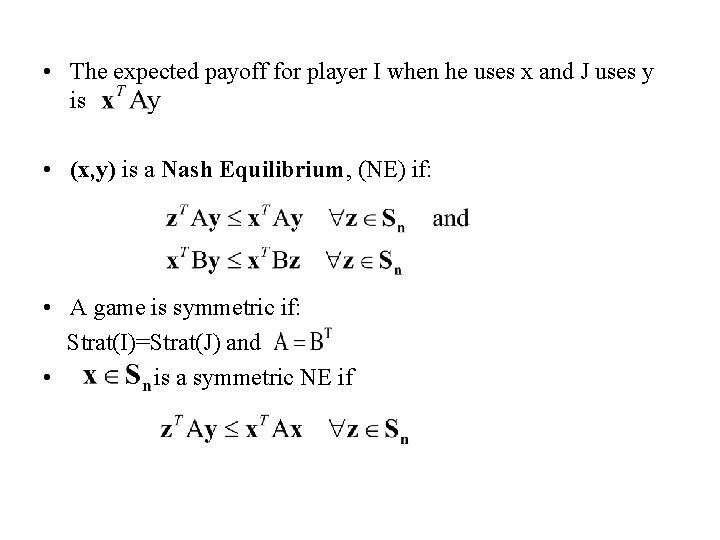
• The expected payoff for player I when he uses x and J uses y is • (x, y) is a Nash Equilibrium, (NE) if: • A game is symmetric if: Strat(I)=Strat(J) and • is a symmetric NE if

Replicator Dynamics • • • Population of n types denotes the frequency of type i State of the population Assume that are differentiable functions of time t Individuals encounter randomly and engage in a symmetric game with payoff matrix A • Expected payoff for an individual of type i: • Average payoff in the population state x:

Replicator Equation Per capita growth:

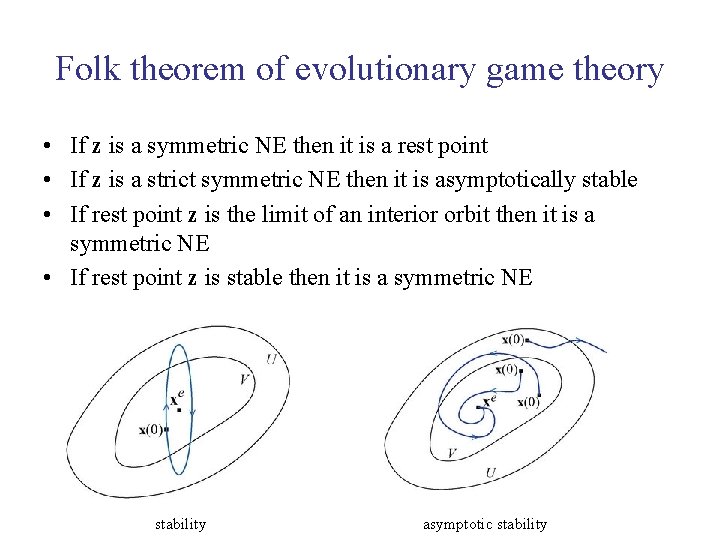
Folk theorem of evolutionary game theory • If z is a symmetric NE then it is a rest point • If z is a strict symmetric NE then it is asymptotically stable • If rest point z is the limit of an interior orbit then it is a symmetric NE • If rest point z is stable then it is a symmetric NE stability asymptotic stability

Existence of NE • 1. 2. Remarks: Every interior rest point is a NE There exists at most one interior rest point, and one rest point for each pure strategy • Theorem: Every game has at least one NE

Evolutionary Stable Strategy (ESS) • Types of population correspond to mixed strategies i=(1, …, N) • Average payoff for an individual type p(i) against an individual of type p(j): • describes the type frequency in the population • Average strategy within the population: • Replicator equation:

• ESS is a strategy which if adopted by a population of players, no alternative strategy that is initially rare can invade • Mutant Strategy: • For a symmetric 2 -player game: Incumbent Strategy: where x is the frequency of the invader • Definition: An ESS in a symmetric 2 -player game is a mixed strategy 1. It is a NE, i. e. 2. If and then if:

Dynamics of two strategy games • Players I, J • Payoff matrix • State of population • Replicator equation: • This equation admits only three outcomes

Hawk-Dove (HD) Game • • • 1. 2. • Large population of animals Occasionally two animals engage in a competition over a pray Two strategies: Hawk: Always fight for pray. Either gets the whole pray or gets injured. Dove: Never fights for pray. Withdraws from Hawk, splits pray with Dove. Payoff matrix:

• • V/2 -C/2 0 u(H, H) u(D, H) (H, H) is the unique symmetric NE and since u(D, D)<u(H, D) (H, H) is the ESS V/2 -C/2<0 We use the replicator equation which here is: Rest points x=1, x=0, x=V/C. Stable interior rest point, the only symmetric NE. Stable coexistence of both types with x=(V/C, 1 -V/C) is the ESS

Prisoners dilemma game • Same assumptions • Payoff matrix • Replicator equation: c>a>d>b • No interior equilibrium, one frequency converges to 0, the other to 1. In this example Fink is the ESS

Coordination Game • Same assumptions • Payoff matrix a>c , d>b • Like Bo. S but in this case both players prefer one outcome over the other • Interior rest point exists and is unstable. The two pure strategies are also NE and both are attracting, bistability Two ESS.

Evolutionary dynamics in competitive routing

Non-cooperative game with finite number of players and infinite space strategy • Model Network {V, L, f} Users i=1, …, N Links l=1, …, M user I sends fixed amount Λi from s(i) to t(i) User i rate on link l: Cost payed from user i for link l: Cost payed from user i for all links used by it • Each user has to determine the way his traffic is split in order to minimize his cost

• • Nash Equilibrium (NE) λ is a Nash equilibrium if: i=1, …, N and strategy of user i Potential game The game admits a potential function P where: • 1. 2. Consequences: NE exists NE is unique • Asynchronous best response updates converge to the unique NE

Replicator Dynamics • User i rate Population i global mass of infinitesimal users • Proportion of population i that uses strategy m: • Cost of users in i that use link l: • The marginal cost of users in i that use link l: • The mean marginal population cost

• Replicator Equation: • If the NE is: and it is an interior rest point the replicator dynamics • The NE is asymptotically stable and any solution trajectory starting from an internal initial condition converges to the NE • So in ESS exists a stable coexistence of the equilibrium flow for all links and all populations

Possible Application Load Balancing • Routing protocol with load dependent metric • Able to perform load balancing across unequal cost links, sending more packets to lower metric routes and vice versa • Replicator dynamic analysis with marginal costs can be implemented in order to find an algorithm that performs optimal load balancing • The algorithm can be executed in routers firmware to ensure optimal routing with load balancing in real time

An application of evolutionary game theory in TCP congestion avoidance

Congestion Control Protocols • Various TCP versions with different congestion avoidance algorithms • Aggressiveness varies from version to version • Examples: TCP New-Reno: approximately AIMD HSTCP: approximately AIMD Scalable TCP: MIMD • AIMD (Additive Increase Multiplicative decrease) algorithm adjusts the flow to the available capacity by increasing the window size by a packets every RTT and when it detects congestion it decreases the window size to b times it’s value. For TCP New-Reno a=1, b=1/2

The Model • Two populations (i=1, 2) of AIMD TCP connections with αi, βi αi linear increase rate βi multiplicative decrease rate xi transmission rate at time t Assumptions: i) RTT same for all connections ii) Light traffic (in terms of connections, not workload) iii) Losses occur whenever sum of rates reaches capacity C: x 1(t)+x 2(t)=C iv) Losses are synchronized • TCP connection i is more aggressive than a connection j if αi ≥ αj and βi ≥ βj • Population dynamics:

• Let xn and yn be the transmission rates of connection i and j, respectively, just before a loss occurs. • We have xn +yn = C. • Just after the loss, the rates are β 1 xn and β 2 yn. The time, measured in RTTs, it takes to reach again C is: which yields the difference equation: where the solution is Where

• Since |q|<1 For • Average throughput of connection 1 • Average loss rate (same for connections 1 and 2) • In wireless networks energy is a costly resource, so loss rate causes energy inefficiency Fitness for player i: where λ is a tradeoff parameter

Evolutionary Stable Strategy • • • Aggressive (Hawk) (αH, βH), Not aggressive (Dove) (αD, βD) For all λ: J(H, H)<J(D, D), J(D, H)<J(D, D), J(H, D) larger than all For small λ: J(H, H)>=J(D, H) so (H, H) is the ESS For large λ: J(H, H)<J(D, H) Mixed HD structure Two versions of TCP will coexist, x is the frequency of the aggressive version • η 1, η 2 positive so equilibrium point x* decrease linearly on λ • Conclusion : Applications that are more sensitive to losses would be less aggressive at ESS

• Classic replicator dynamics: The fitness acquired at time t has an impact on the rate of growth of the population size that uses it instantly. • Replicator dynamics with delay (More realistic model) The fitness acquired at time t will impact the rate of growth τ time later • K positive constant, accelerates the speed of convergence to the ESS • The delay τ is related to the time scale for example of switching from the use of one protocol to another or upgrading a protocol

• Replicator dynamics with delay yield to the mixed ESS if: τK<θ where • For the evolutionary protocol to converge to an ESS the product τK must have a constant value and smaller than θ • For large delay τ, the fitness of a strategy acquired at t-τ should have a smaller impact on the rate of growth and hence slower convergence to the mixed ESS

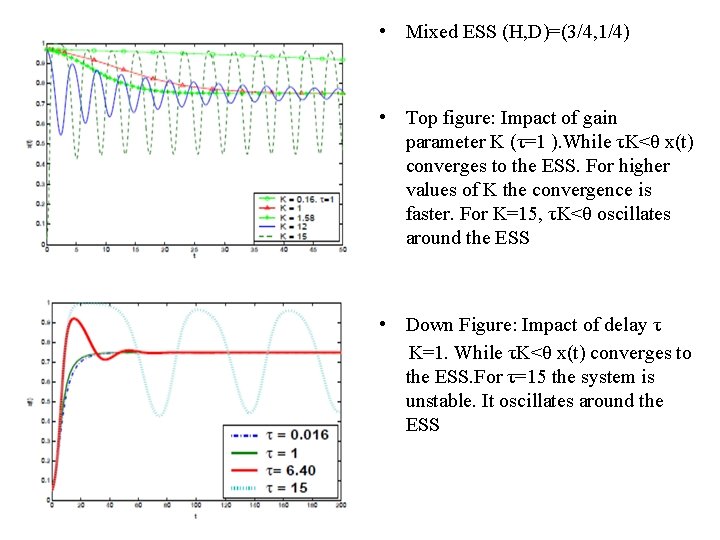
• Mixed ESS (H, D)=(3/4, 1/4) • Top figure: Impact of gain parameter K (τ=1 ). While τK<θ x(t) converges to the ESS. For higher values of K the convergence is faster. For K=15, τK<θ oscillates around the ESS • Down Figure: Impact of delay τ K=1. While τK<θ x(t) converges to the ESS. For τ=15 the system is unstable. It oscillates around the ESS

Evolutionary Games and Population Dynamics Maintenance of cooperation on public goods games

Evolutionary Games and Population Dynamics: Maintenance of cooperation on public goods games The problem of cooperation investigated by means of the game theoretical models of: 1)Prisoners Dilemma for pair wise interactions 2)Public Goods Games for groups or interacting individuals Public Goods Games: Subjects(players) secretly choose how many of their private tokens to put into a public pot. Each subject keeps the tokens they do not contribute +even split of the tokens in the pot -Contributors: ”cooperators “ -Those who do not contribute: ”defectors” or “free riders” Payoffs: PD(k)=rkc/N PC(k)= PD(k)-c N-size of the group, k-number of cooperators, c-cost, r-multiplication factor for N=2 it can be mapped onto Prisoners Dilemma

Public Good Games: Basic Idea • When population density varies=>Effective group size S of the public goods varies • Small population densities => Small S (and vice versa) • Large population densities favors defection Defection leads to a decrease in population density and hence a decrease in S which in turn, favors cooperation

GAME DYNAMICS AND POPULATION DYNAMICS Fraction of cooperators : x Fraction of defectors : y Fraction of empty space : z=1 -x-y Normalized population density x+y (0=extinction, 1=maximal population density) fc , f. D average payoffs of cooperators and defectors respectively at any point of time d- constant death rate and birth rate proportional to average payoffs and z Population Dynamic Model: (Natural extension of replicator dynamics) The average fitness of defectors and cooperators can be given: where

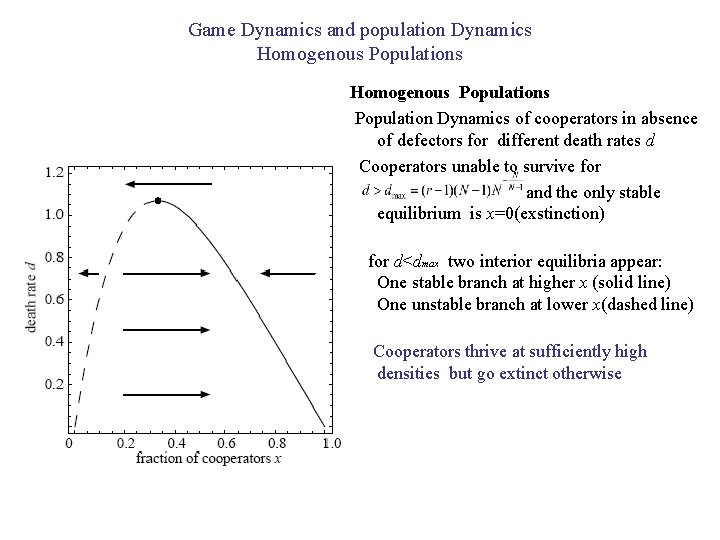
Game Dynamics and population Dynamics Homogenous Populations Population Dynamics of cooperators in absence of defectors for different death rates d Cooperators unable to survive for and the only stable equilibrium is x=0(exstinction) for d<dmax two interior equilibria appear: One stable branch at higher x (solid line) One unstable branch at lower x(dashed line) Cooperators thrive at sufficiently high densities but go extinct otherwise

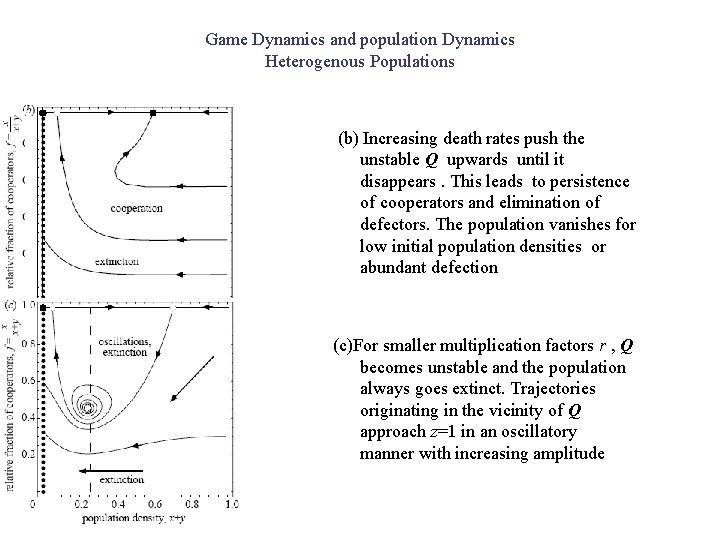
Game Dynamics and population Dynamics Heterogenous Populations Cooperators survive even when facing exploitation by defectors. The relative proportion of cooperators is f=x/(x+y) and we have: There are four different dynamic systems depending on the existence of interior equilibrium points. Equilibrium points are of the form where solves and (a) Q exists and is a stable focus. Cooperators and defectors can coexist. Trajectories spiral towards Q , except for low population densities or abundant defection, in which case population goes extinct.

Game Dynamics and population Dynamics Heterogenous Populations (b) Increasing death rates push the unstable Q upwards until it disappears. This leads to persistence of cooperators and elimination of defectors. The population vanishes for low initial population densities or abundant defection (c)For smaller multiplication factors r , Q becomes unstable and the population always goes extinct. Trajectories originating in the vicinity of Q approach z=1 in an oscillatory manner with increasing amplitude

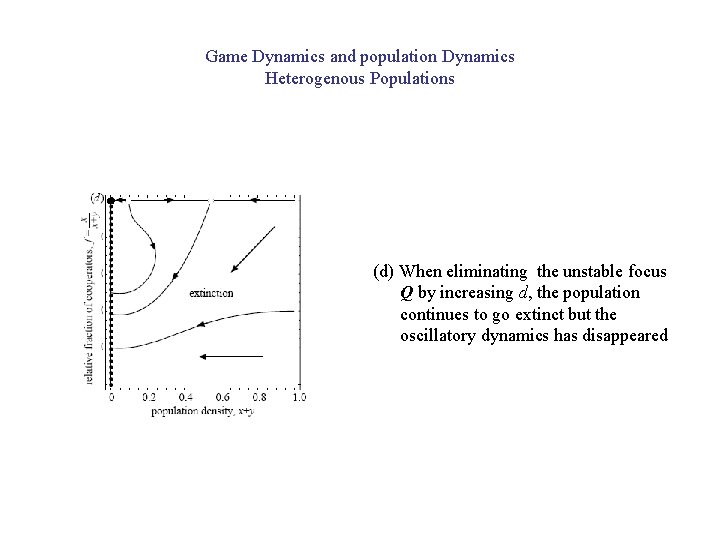
Game Dynamics and population Dynamics Heterogenous Populations (d) When eliminating the unstable focus Q by increasing d, the population continues to go extinct but the oscillatory dynamics has disappeared

Possible application in P 2 P networks • • • P 2 P network of N nodes Nodes controlled by selfish users Cooperators: Download and caching files Defectors: Only download, not caching files Large population densities favors defection leading to a decrease in population density and hence a decrease in effective interaction group which in turn favors cooperation • For intermediate frequencies of populations we can have a stable coexistence of both types or dominance of cooperators

Possible application in mobile ad-hoc networks • Mobile ad-hoc network with N nodes • Each node supports a multihop routing algorithm where nodes function as relays • Nodes are equipped with non-replenishable energy sources • Selfish behavior: conserve power, don't act as relays • Cooperative behavior: act as relays • Large population densities favors defection leading to a decrease in population density and hence a decrease in effective interaction group which in turn favors cooperation • For intermediate frequencies of populations we can have a stable coexistence of both types or dominance of cooperators

Congestion control for applications sensitive to delay • Applications sensitive to delay prefer UDP over TCP • The congestion control is implemented by the applications • Dynamic rate adjustment by the application during the session by degrading for example the amount of redundancy • When a congestion event is detected the rate is reduced • Aggressive sessions may not reduce the rate at the first congestion event waiting to see if the congestion has been eliminated through the other sessions reducing the rate • Or aggressive sessions may reduce the rate at the first congestion event but the reduction is smaller than the one that takes place in the non-aggressive sessions • Evolutionary game theory can predict the dominance or coexistence of the different protocols

References • J. Hofbauer, K. Sigmund. Evolutionary Game Dynamics. Bulletin (New Series) of the American Mathematical Society. Volume 40, Number 4, Pages 479 -519 • R. Cressman. Evolutionary Dynamics and extensive form games. The MIT Press • E. Altman, Y. Hayel, H. Kameda. Evolutionary dynamics and potential games in non-cooperative routing. INRIA Sophia Antipolis. • E. Altman, R. El. Azouzi, Y. Hayel, H. Tembine. An Evolutionary Game approach for the design of congestion control protocols in wireless networks. INRIA Sophia Antipolis. • C. Hauert, M. Holmes, M. Doebeli. Evolutionary games and population dynamics: maintenance of cooperation in public good games. Proc. R. Soc. B 2006 273, 2565 -2571
 Evolutionary theory of motivation
Evolutionary theory of motivation Evolutionary theory of motivation
Evolutionary theory of motivation What do we call a need or desire that energizes behavior
What do we call a need or desire that energizes behavior Hunger games hierarchy
Hunger games hierarchy Evolutionary theory of motivation
Evolutionary theory of motivation Strengths and weaknesses of evolutionary theory page 386
Strengths and weaknesses of evolutionary theory page 386 Section 3 shaping evolutionary theory
Section 3 shaping evolutionary theory Chapter 15 section 3 shaping evolutionary theory
Chapter 15 section 3 shaping evolutionary theory Stages of religion
Stages of religion Centipede arcade game
Centipede arcade game Pirate grid game
Pirate grid game Game lab game theory
Game lab game theory Liar game game theory
Liar game game theory Liar game game theory
Liar game game theory Selfish giant summary
Selfish giant summary Selfish in asl
Selfish in asl Stubborn synoyms
Stubborn synoyms The selfish giant oscar wilde analysis
The selfish giant oscar wilde analysis Was the giant happy or sad over the state of the garden
Was the giant happy or sad over the state of the garden Define selfish
Define selfish Is survival selfish by lane wallace
Is survival selfish by lane wallace Funny comparative form
Funny comparative form The selfish giant oscar wilde
The selfish giant oscar wilde Comparative the
Comparative the Lift not the painted veil analysis
Lift not the painted veil analysis Shy sociable talkative stubborn
Shy sociable talkative stubborn Every afternoon as they were coming
Every afternoon as they were coming Wlearning
Wlearning Game theory and graph theory
Game theory and graph theory Embouchure tips for brass players
Embouchure tips for brass players Irish baseball players
Irish baseball players Colin took a sample of 80 football players
Colin took a sample of 80 football players Rules of snooker
Rules of snooker The major key players on the international side are the:
The major key players on the international side are the: The evolution of music players
The evolution of music players Characteristics of sustainable tourism
Characteristics of sustainable tourism Which company is recognized as the inventor of cruising
Which company is recognized as the inventor of cruising The three players in the money supply process include
The three players in the money supply process include Agility in table tennis
Agility in table tennis Why football players should wrestle
Why football players should wrestle Team vs working group
Team vs working group The songs listed below belong to the different
The songs listed below belong to the different A basketball is being pushed by two players
A basketball is being pushed by two players