Evolutionary Game Theory Game Theory Von Neumann Morgenstern

Evolutionary Game Theory

Game Theory • Von Neumann & Morgenstern (1953) Studying economic behavior • Maynard Smith & Price (1973) Why are animal conflicts examples of ‘limited wars’?

Assumptions • • • Infinite population size Random mating Asexual reproduction Frequency dependent fitness Genotype can be mapped directly onto phenotype - haplotypes

Fundamental Concept • The Evolutionary Stable Strategy (ESS) “A strategy such that if all members of the population adopt it, then no mutant can invade the population under the influence of selection”

The Haploid Hawk Dove Game • Consider two haplod virus genotypes that breed true • The Hawk genotype encodes a virulent virus strain. • The Dove genotype encodes an avirulent virus strain

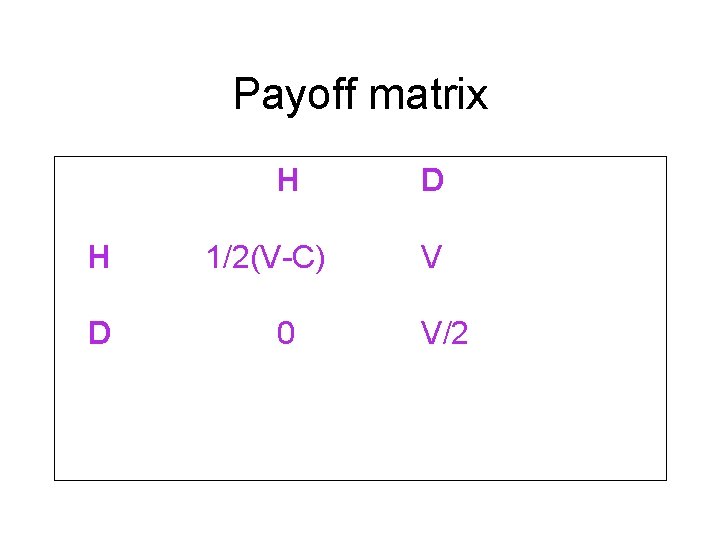
Fitness payoffs • • The reproductive value of an infected host to a virus is V When two virulent viruses (H) coinfect a host there is a cost associated with morbidity C When a virulent virus (H) coinfects with a avirulent virus (D), H derives all the benefits V. When two avirulent viruses (D) infect a host they obtain approximately half of the resource each V/2

Payoff matrix H H D 1/2(V-C) 0 D V V/2

Building the model • p = frequency of H viruses • W(H) & W(D), denote mean fitness • E(H, D) fitness payoff to H infecting a body already infected with D, similar meaning for E(H, H), E(D, H) and E(D, D) • W 0 is the fitness of the virus prior to infection of the host

Virus fitnesses • Upon infection of a single host: W(H) = W 0+ p. E(H, H) + (1 -p)E(H, D) W(D) = W 0 + p. E(D, H) + (1 -p)E(D, D)

Determining the ESS conditions • • • Consider any two genotypes I & J: W(I) = W 0 + p. E(I, J) + (1 -p)E(I, I) W(J) = W 0 + p. E(J, J) + (1 -p)E(J, I) Assume that I is an ESS and J is a rare mutant with frequency p If I is an ESS then W(I) > W(J), assuming that p <<1, then, E(I, I) > E(J, I) or (Invasion condition) E(I, I) = E(J, I) and E(I, J) > E(J, J) (Stability)

ESS solutions to the H & D game • E(I, I) > E(J, I) or (Invasion condition) E(I, I) = E(J, I) and E(I, J) > E(J, J) (Stability) • E(D, D) > E(H, D) Never! • E(H, H) > E(D, H) only of 1/2(V-C) > 0

Mixed ESS solutions • • What if V<C? Does this mean that there is no ESS solution to the game? An alternative ESS solution can exist if the biology permits. This requires either a genotype capable of switching between H and D or some mix of H & D coexisting in the population.

Mixed ESS solution • Consider strategy I as genotype H with probability P and genotype D with probability (1 -P). • For a mixed ESS to exist then: E(A, I) = E(B, I) = E(C, I)…= E(I, I) All pure strategies in support of I must have the same payoff.

Finding the mixed ESS • If I is a mixed ESS then E(H, I)= E(D, I): • E(H, I) = PE(H, H) + (1 -P)E(H, D) • E(D, I) = PE(D, H) + (1 -P)E(D, D) • P(1/2)(V-C) + (1 -P)V = P. 0 + (1 -P)V/2 • Solve for P • P = V/C

Testing I with the ESS conditions • E(I, I) > E(J, I) or (Invasion condition) E(I, I) = E(J, I) and E(I, J) > E(J, J) (Stability) • We need to see if I meets the stability condition: E(H, I) = E(D, I) = E(I, I) (True) • Therefore we require that: E(I, D) > E(D, D) & E(I, H) > E(H, H) • Calculate the above and show that I is an ESS

Evolution of virulence genes • When V > C then virulent virus always favoured • When V < C then some proportion of the population given by V/C will be virulent • Increasing the cost favours avirulent forms • Reducing the cost favours the virulent forms

Game Theory Summary • Fitness of a gene can depend on frequencies of all other genes in a population -- fitness is frequency dependent • Game theory provides a tool for determining the equilibrium distribution of genotypes in the population when fitness is frequency dependent • Key Reference: John Maynard Smith. Evolution and the Theory of Games. CUP. 1982.

Game theory: anisogamy

Game Theory: the sex ratio

Game theory: area of application • • • Frequency-dependent selection Ignorant about genetic mechanisms Parthenogenetic inheritance Act as an aid to intuition before building more complex models When we do know about genetics it is best to add selection to our population genetics models