Elments Rduction 1 Une poutre droite de longueur

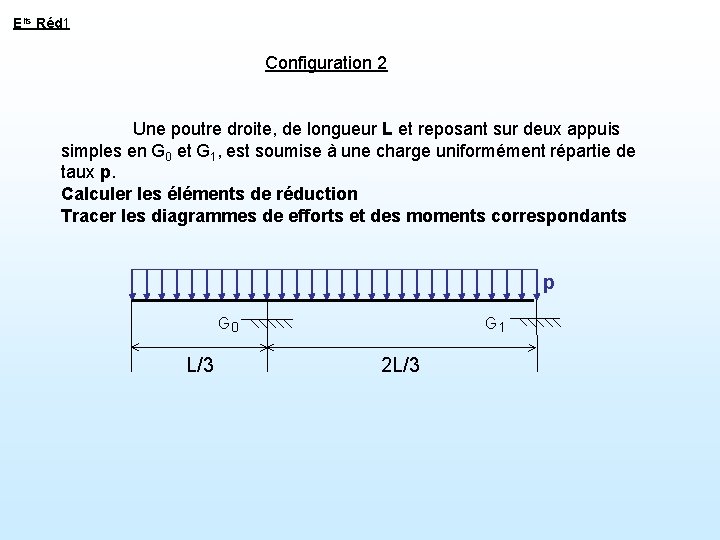
Eléments Réduction 1 Une poutre droite, de longueur L et reposant sur deux appuis simples en G 0 et G 1, est soumise à une charge uniformément répartie de taux p. Calculer les éléments de réduction pour chaque configuration Tracer les diagrammes de efforts et des moments correspondants Configuration 1 Configuration 2

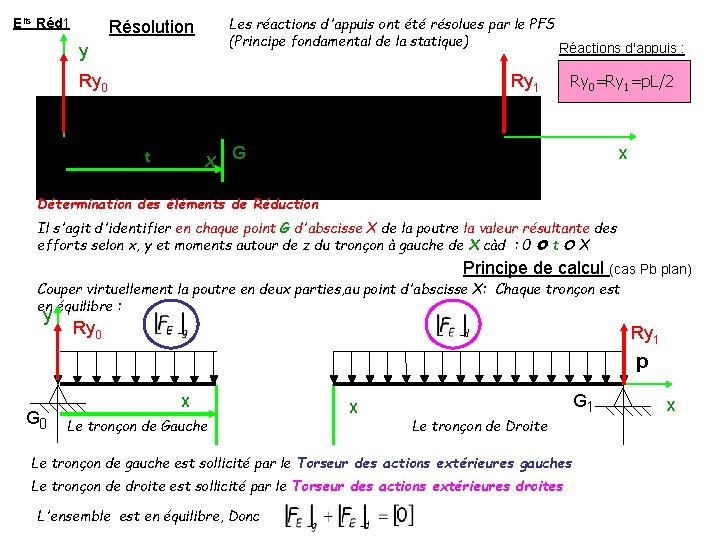
Elts Réd 1 Les réactions d'appuis ont été résolues par le PFS (Principe fondamental de la statique) Résolution y Ry 0 Réactions d'appuis : Ry 1 t X Ry 0=Ry 1=p. L/2 x G Détermination des éléments de Réduction Il s'agit d'identifier en chaque point G d'abscisse X de la poutre la valeur résultante des efforts selon x, y et moments autour de z du tronçon à gauche de X càd : 0 t X Principe de calcul (cas Pb plan) Couper virtuellement la poutre en deux parties, au point d'abscisse X: Chaque tronçon est en équilibre : y Ry 0 Ry 1 p G 0 X Le tronçon de Gauche X G 1 Le tronçon de Droite Le tronçon de gauche est sollicité par le Torseur des actions extérieures gauches Le tronçon de droite est sollicité par le Torseur des actions extérieures droites L'ensemble est en équilibre, Donc x

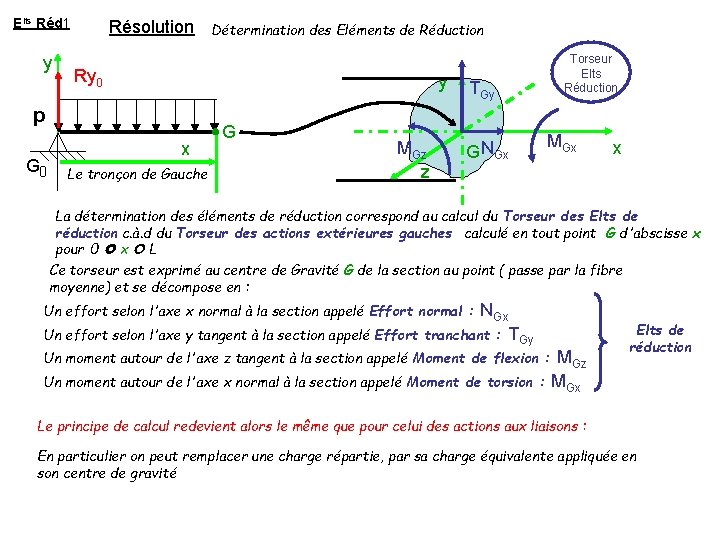
Elts Réd 1 y Résolution Ry 0 y p G 0 Détermination des Eléments de Réduction G X Le tronçon de Gauche MGz z Torseur Elts Réduction TGy G NGx MGx x La détermination des éléments de réduction correspond au calcul du Torseur des Elts de réduction c. à. d du Torseur des actions extérieures gauches calculé en tout point G d'abscisse x pour 0 x L Ce torseur est exprimé au centre de Gravité G de la section au point ( passe par la fibre moyenne) et se décompose en : NGx tranchant : TGy Un effort selon l'axe x normal à la section appelé Effort normal : Un effort selon l'axe y tangent à la section appelé Effort Un moment autour de l'axe z tangent à la section appelé Moment de flexion : Un moment autour de l'axe x normal à la section appelé Moment de torsion : MGz MGx Elts de réduction Le principe de calcul redevient alors le même que pour celui des actions aux liaisons : En particulier on peut remplacer une charge répartie, par sa charge équivalente appliquée en son centre de gravité

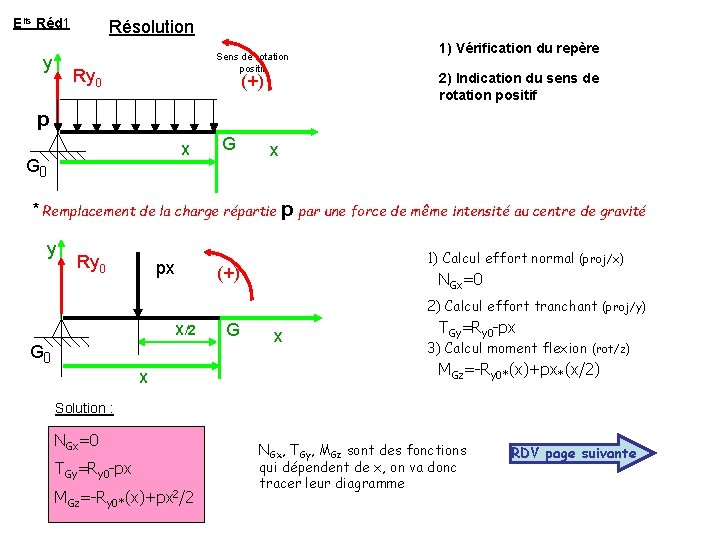
Elts Réd 1 y Résolution Sens de rotation positif Ry 0 (+) 1) Vérification du repère 2) Indication du sens de rotation positif p X G 0 G x * Remplacement de la charge répartie p par une force de même intensité au centre de gravité y Ry 0 px 1) Calcul effort normal (proj/x) (+) NGx=0 2) Calcul effort tranchant (proj/y) X/2 G 0 X G x TGy=Ry 0 -px 3) Calcul moment flexion (rot/z) MGz=-Ry 0*(x)+px*(x/2) Solution : NGx=0 TGy=Ry 0 -px MGz=-Ry 0*(x)+px 2/2 NGx, TGy, MGz sont des fonctions qui dépendent de x, on va donc tracer leur diagramme RDV page suivante

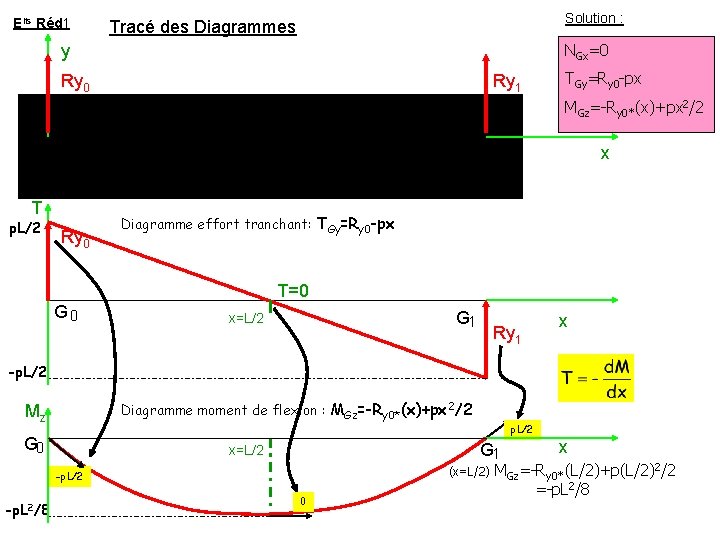
Elts Réd 1 Solution : Tracé des Diagrammes NGx=0 y Ry 0 Ry 1 TGy=Ry 0 -px MGz=-Ry 0*(x)+px 2/2 x T p. L/2 Ry 0 Diagramme effort tranchant: TGy=Ry 0 -px T=0 G 1 x=L/2 Ry 1 x -p. L/2 Diagramme moment de flexion : MGz=-Ry 0*(x)+px 2/2 Mz G 0 G 1 x=L/2 (x=L/2) -p. L/2 -p. L 2/8 p. L/2 0 x MGz=-Ry 0*(L/2)+p(L/2)2/2 =-p. L 2/8

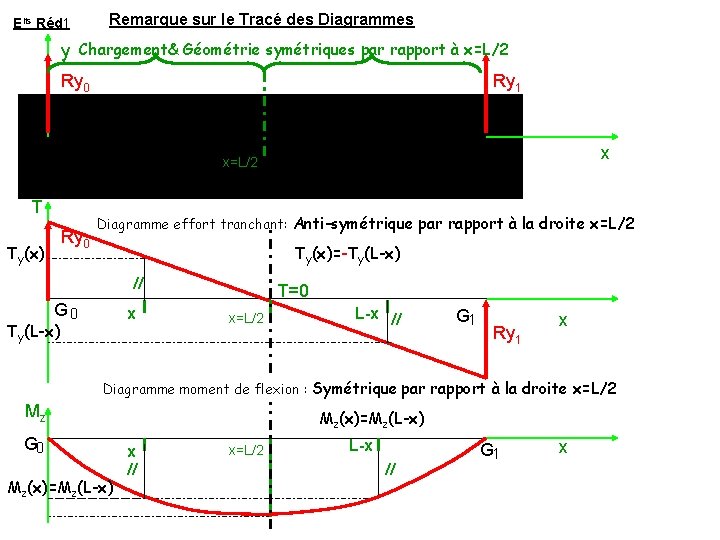
Elts Réd 1 Remarque sur le Tracé des Diagrammes y Chargement& Géométrie symétriques par rapport à x=L/2 Ry 0 Ry 1 x x=L/2 T Ry 0 Ty(x) Diagramme effort tranchant: Anti-symétrique par rapport à la droite x=L/2 Ty(x)=-Ty(L-x) // G 0 x Ty(L-x) T=0 x=L/2 L-x // G 1 Ry 1 x Diagramme moment de flexion : Symétrique par rapport à la droite x=L/2 Mz G 0 Mz(x) =Mz(L-x) Mz(x)=Mz(L-x) x // x=L/2 L-x // G 1 x

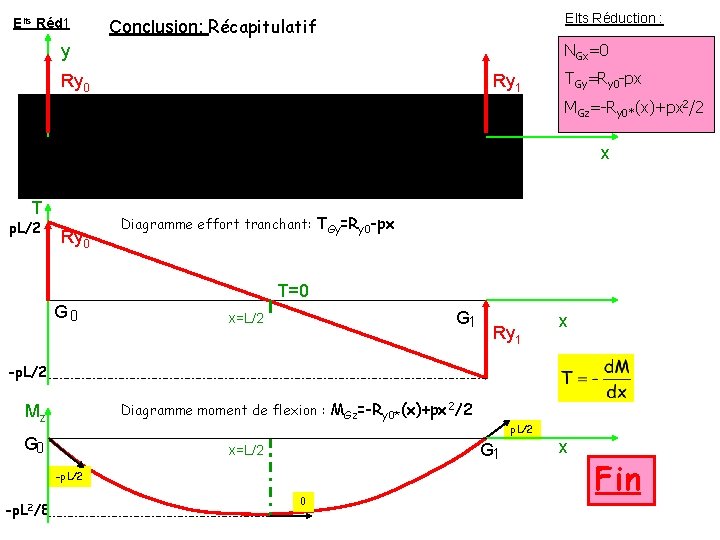
Elts Réd 1 Elts Réduction : Conclusion: Récapitulatif NGx=0 y Ry 0 Ry 1 TGy=Ry 0 -px MGz=-Ry 0*(x)+px 2/2 x T p. L/2 Ry 0 Diagramme effort tranchant: TGy=Ry 0 -px T=0 G 1 x=L/2 Ry 1 x -p. L/2 Diagramme moment de flexion : MGz=-Ry 0*(x)+px 2/2 Mz G 0 G 1 x=L/2 -p. L 2/8 p. L/2 0 x Fin

Elts Réd 1 Configuration 2 Une poutre droite, de longueur L et reposant sur deux appuis simples en G 0 et G 1, est soumise à une charge uniformément répartie de taux p. Calculer les éléments de réduction Tracer les diagrammes de efforts et des moments correspondants p G 0 L/3 G 1 2 L/3

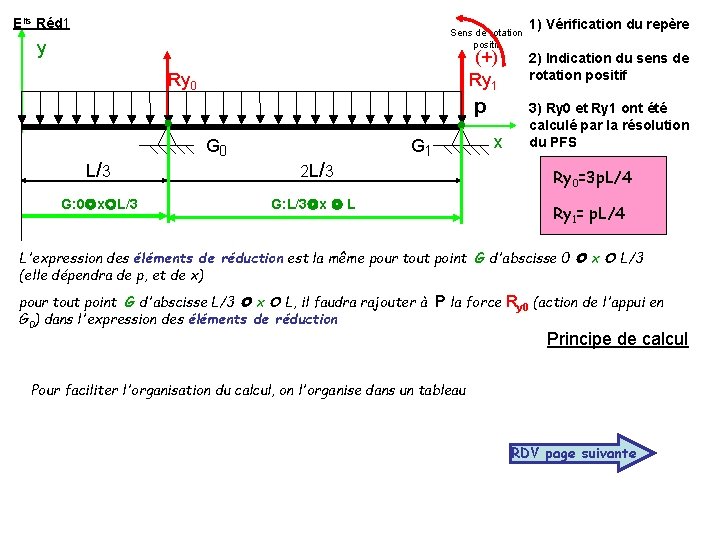
Elts Réd 1 Sens de rotation positif y Ry 0 L/ 3 G: 0 x L/3 G 0 2 L/ 3 G 1 G: L/3 x L 1) Vérification du repère (+) Ry 1 2) Indication du sens de rotation positif p 3) Ry 0 et Ry 1 ont été calculé par la résolution du PFS x Ry 0=3 p. L/4 Ry 1= p. L/4 L'expression des éléments de réduction est la même pour tout point G d'abscisse 0 x L/3 (elle dépendra de p, et de x) pour tout point G d'abscisse L/3 x L, il faudra rajouter à P la force Ry 0 (action de l'appui en G 0) dans l'expression des éléments de réduction Principe de calcul Pour faciliter l'organisation du calcul, on l'organise dans un tableau RDV page suivante

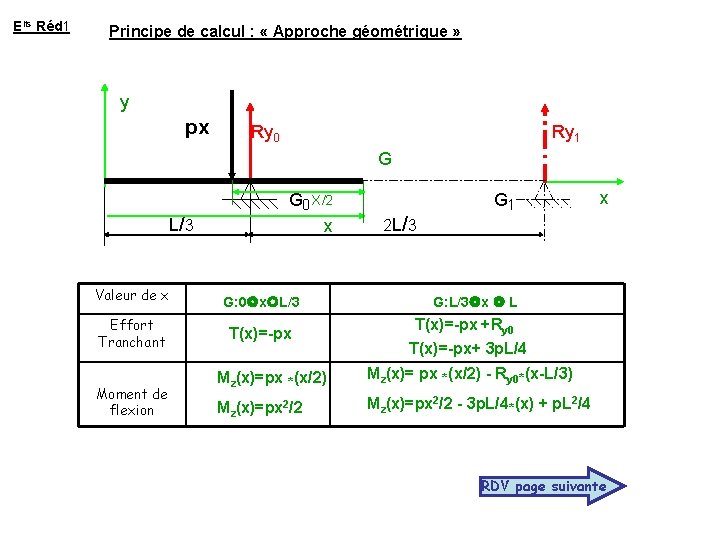
Elts Réd 1 Principe de calcul : « Approche géométrique » y pxpx p p Ry 0 X/2 x L/ 3 Effort Tranchant Moment de flexion p G G Valeur de x Ry 11 Ry G 0 X/2 x G: 0 x L/3 T(x)=-px 2 L/ 3 G 1 x G: L/3 x L T(x)=-px +Ry 0 T(x)=-px+ 3 p. L/4 Mz(x)=px *(x/2) Mz(x)= px *(x/2) - Ry 0*(x-L/3) Mz(x)=px 2/2 - 3 p. L/4*(x) + p. L 2/4 RDV page suivante

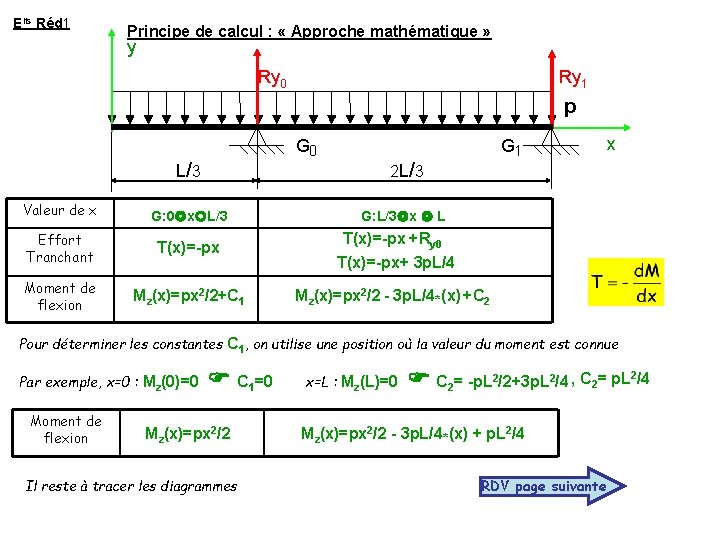
Elts Réd 1 Principe de calcul : « Approche mathématique » y Ry 0 Ry 1 p G 0 L/ 3 Valeur de x G: 0 x L/3 Effort Tranchant T(x)=-px Moment de flexion Mz(x)=px 2/2+C 1 G 1 2 L/ 3 x G: L/3 x L T(x)=-px +Ry 0 T(x)=-px+ 3 p. L/4 Mz(x)=px 2/2 - 3 p. L/4*(x) +C 2 Pour déterminer les constantes C 1, on utilise une position où la valeur du moment est connue Par exemple, x=0 : Mz(0)=0 Moment de flexion C 1=0 Mz(x)=px 2/2 Il reste à tracer les diagrammes x=L : Mz(L)=0 C 2= -p. L 2/2+3 p. L 2/4 , C 2= p. L 2/4 Mz(x)=px 2/2 - 3 p. L/4*(x) + p. L 2/4 RDV page suivante

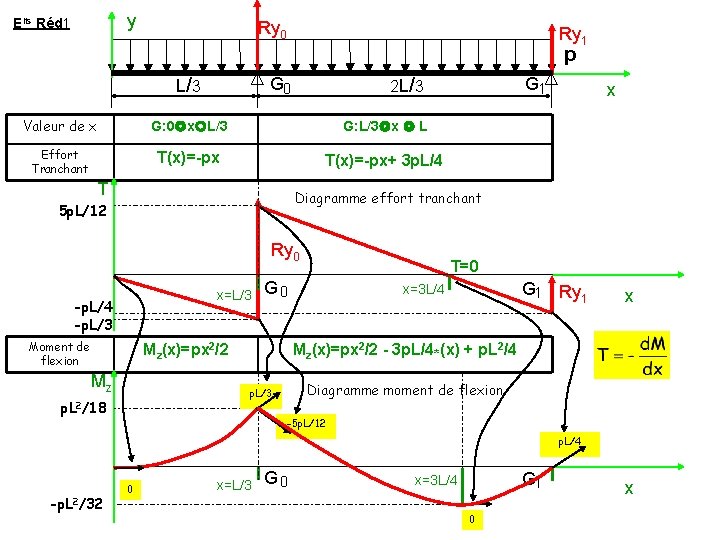
y Elts Réd 1 Ry 0 Ry 1 p G 0 L/ 3 Valeur de x G: 0 x L/3 G: L/3 x L Effort Tranchant T(x)=-px+ 3 p. L/4 T G 1 2 L/ 3 x Diagramme effort tranchant 5 p. L/12 Ry 0 x=L/3 -p. L/4 -p. L/3 Moment de flexion G 0 Mz(x)=px 2/2 Mz G 1 Ry 1 x=3 L/4 x Mz(x)=px 2/2 - 3 p. L/4*(x) + p. L 2/4 Diagramme moment de flexion p. L/3 p. L 2/18 T=0 -5 p. L/12 p. L/4 -p. L 2/32 0 x=L/3 G 0 G 1 x=3 L/4 0 x

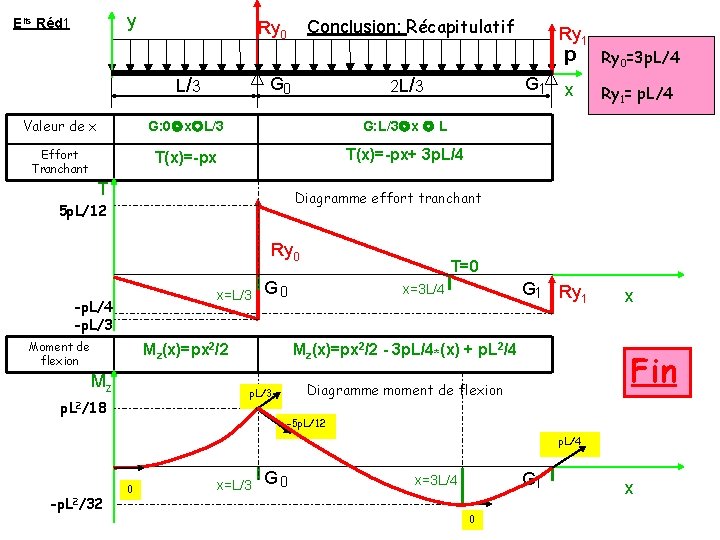
y Elts Réd 1 Conclusion: Récapitulatif Ry 0 G 0 L/ 3 G 1 2 L/ 3 Valeur de x G: 0 x L/3 G: L/3 x L Effort Tranchant T(x)=-px+ 3 p. L/4 T Ry 1 p Ry 0=3 p. L/4 x Ry 1= p. L/4 Diagramme effort tranchant 5 p. L/12 Ry 0 x=L/3 -p. L/4 -p. L/3 Moment de flexion G 0 Mz(x)=px 2/2 Mz G 1 Ry 1 x=3 L/4 Mz(x)=px 2/2 - 3 p. L/4*(x) + p. L 2/4 x Fin Diagramme moment de flexion p. L/3 p. L 2/18 T=0 -5 p. L/12 p. L/4 -p. L 2/32 0 x=L/3 G 0 G 1 x=3 L/4 0 x

Elts Réd 1 Exemple Une poutre droite, de longueur L et reposant sur deux appuis simples en G 0 et G 1, est soumise à une charge uniformément répartie de taux p, et une force F=-p. L et un couple M=p. L 2/5. Calculer les éléments de réduction Tracer les diagrammes de efforts et des moments correspondants F=p. L M=p. L 2/5 p G 0 L/3 G 1 2 L/3

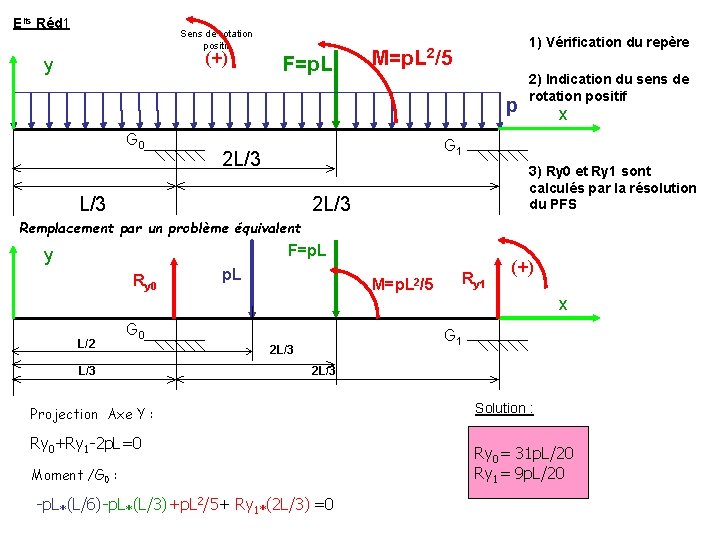
Elts Réd 1 Sens de rotation positif (+) y F=p. L 1) Vérification du repère M=p. L 2/5 p G 0 2) Indication du sens de rotation positif x G 1 2 L/3 3) Ry 0 et Ry 1 sont calculés par la résolution du PFS 2 L/3 Remplacement par un problème équivalent F=p. L y Ry 0 p. L M=p. L 2/5 Ry 1 (+) x L/2 G 0 L/3 G 1 2 L/3 Projection Axe Y : Ry 0+Ry 1 -2 p. L=0 Moment /G 0 : -p. L*(L/6) -p. L*(L/3) +p. L 2/5+ Ry 1*(2 L/3) =0 Solution : Ry 0= 31 p. L/20 Ry 1= 9 p. L/20

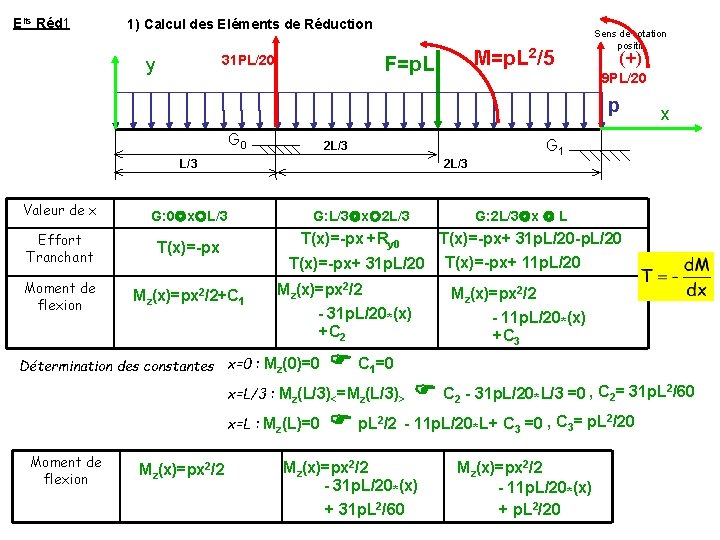
Elts Réd 1 1) Calcul des Eléments de Réduction M=p. L 2/5 F=p. L 31 PL/20 y Sens de rotation positif (+) 9 PL/20 p G 0 2 L/3 Valeur de x 2 L/3 G: 0 x L/3 Effort Tranchant T(x)=-px Moment de flexion Mz(x)=px 2/2+C 1 G: L/3 x 2 L/3 G: 2 L/3 x L T(x)=-px+ 31 p. L/20 -p. L/20 T(x)=-px+ 31 p. L/20 T(x)=-px+ 11 p. L/20 Mz(x)=px 2/2 - 31 p. L/20*(x) +C 2 x=L : Mz(L)=0 Mz(x)=px 2/2 - 11 p. L/20*(x) +C 3 C 1=0 x=L/3 : Mz(L/3)<=Mz(L/3)> Mz(x)=px 2/2 G 1 T(x)=-px +Ry 0 Détermination des constantes x=0 : Mz(0)=0 Moment de flexion x C 2 - 31 p. L/20*L/3 =0 , C 2= 31 p. L 2/60 p. L 2/2 - 11 p. L/20*L+ C 3 =0 , C 3= p. L 2/20 Mz(x)=px 2/2 - 31 p. L/20*(x) + 31 p. L 2/60 Mz(x)=px 2/2 - 11 p. L/20*(x) + p. L 2/20

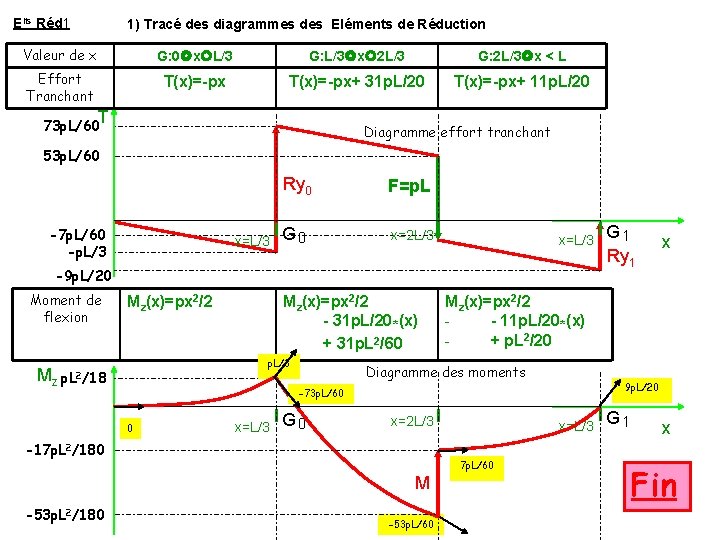
Elts Réd 1 1) Tracé des diagrammes des Eléments de Réduction Valeur de x G: 0 x L/3 G: L/3 x 2 L/3 G: 2 L/3 x < L Effort Tranchant T(x)=-px+ 31 p. L/20 T(x)=-px+ 11 p. L/20 T 73 p. L/60 Diagramme effort tranchant 53 p. L/60 -7 p. L/60 -p. L/3 x=L/3 Ry 0 F=p. L G 0 x=2 L/3 x=L/3 -9 p. L/20 Moment de flexion Mz Mz(x)=px 2/2 - 31 p. L/20*(x) + 31 p. L 2/60 p. L/3 p. L 2/18 x=L/3 Diagramme des moments G 0 x=2 L/3 -17 p. L 2/180 -53 p. L 2/180 9 p. L/20 x=L/3 7 p. L/60 M -53 p. L/60 x Mz(x)=px 2/2 - 11 p. L/20*(x) + p. L 2/20 -73 p. L/60 0 G 1 Ry 1 G 1 x Fin

Elts Réd 1 Fin Elts de Réduction 1