Electric fields in material space Equation of Continuity

Electric fields in material space Equation of Continuity Boundary conditions Capacitance

Module I �Introduction to EMFT �Coordinate systems and transformations �Vector fields, Divergence and curl �Divergence and Stokes theorem �Electric fields, Electric scalar potential �Types of potential distribution, Potential Gradient �Energy stored, Electric boundary conditions, Capacitance �Steady current and current density, Equation of continuity �Magnetic fields, Energy stored �Magnetic dipole �Magnetic boundary conditions �Vector magnetic potential, Magnetic field intensity

Boundary Conditions �Helpful in determining the field on one side of the boundary if the field on the other side is known. �Steps: Use Maxwell’s Equations � 1) Decompose Electric field into orthogonal components, apply maxwell’s eqn � 2) Similarly, decompose Electric flux density D.

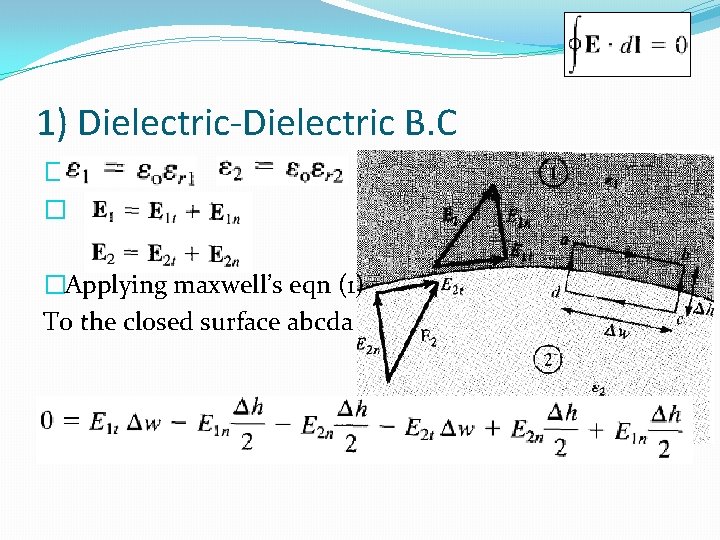
1) Dielectric-Dielectric B. C � � �Applying maxwell’s eqn (1) To the closed surface abcda

1) Dielectric-Dielectric B. C �When we consider that (Tangential components of E are same at both sides) �Et is said to be continuous across the boundary. �Since , �So Dt undergoes some changes across the boundary �Dt is discontinuous across the boundary.

1) Dielectric-Dielectric B. C �At �If no free charges exists , �So, Dn is continuous across the interface. En is discontinuous across the interface

Summarizing �Dt is discontinuous across the interface. �Et is continuous across the boundary. �Dn is continuous across the interface. �En is discontinuous across the boundary. �These equations are collectively called as electric boundary conditions. �Used for finding the field at one side of the boundary if the field at the other surface is known. �Used for finding the refraction of the electric field across the boundary

Relation Between Angle of Incidence and Permittivity Refraction (Dielectric-Dielectric) �Consider E 1/E 2 making Angles with normal Dividing,

Conductor-Dielectric B. C �For the conductor, E = 0 for the conductor. �Follow same steps for the Dielectric-dielectric interface But consider that E=0 inside the metallic portion

Applying eqns to the pillbox, � ( � )

For a perfect conductor,

Applications: �Electrostatic screening

Conductor-Free space B. C �Special case of conductor-dielectric B. C �Replace �

Capacitance (Farads) �Ability of a body to hold an electrical charge. � 2 conductors with equal but opposite charges �Flux lines leaving one conductor must necessarily terminate at the surface of the other conductor.

Capacitors �The conductors are sometimes referred to as the plates of the capacitor. �The plates may be separated by free space or a ielectric.

Capacitance �Consider a 2 conductor capacitor � �E field will be normal to the surface �We define the capacitance C of the capacitor as the ratio of the magnitude of the charge on one of the plates to the potential difference between them � ( )

Finding the capacitance (Steps) 1. Choose a suitable coordinate system. 2. Let the two conducting plates carry charges + Q and -Q. 3. Determine E using Coulomb's or Gauss's law and find V from 4. Obtain C from C=Q/V � Parallel Plate Capacitor � Coaxial Capacitor � Spherical Capacitor

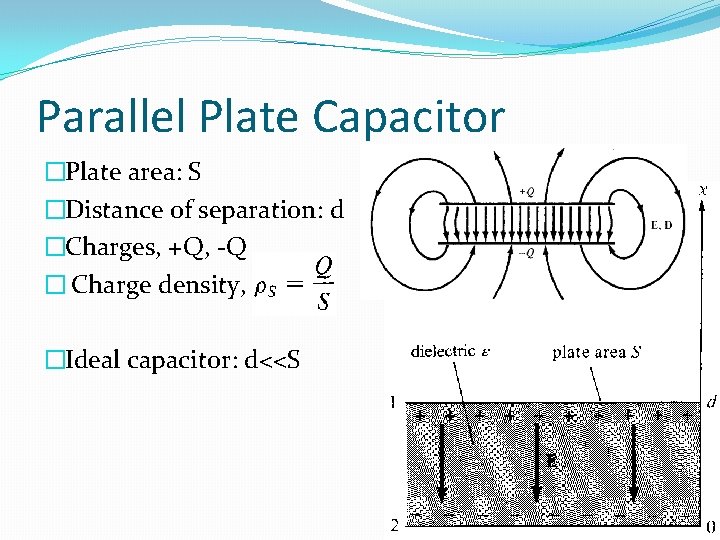
Parallel Plate Capacitor �Plate area: S �Distance of separation: d �Charges, +Q, -Q � Charge density, �Ideal capacitor: d<<S

Parallel Plate Capacitor �According to coulomb’s law, � � (Derivation not needed) �So for a parallel plate capacitor, � (C 0: Capacitance when air is between plates) �Energy stored,

Coaxial Capacitor �By applying Gauss’ Law, � �Potential Difference, �Capacitance is given by, ea Surface ar

Spherical Capacitor � �

Special cases �If the outer plate of a capacitor is infinitely large, � (Spherical conductor at a large distance from other conducting bodies – isolated sphere) � Notes � �If & , we can say �This expression gives the relaxation time, Tr