Electric Fields Review of gravitational fields Electric field












































- Slides: 55

Electric Fields • Review of gravitational fields • Electric field vector • Electric fields for various charge configurations • Field strengths for point charges and uniform fields • Work done by fields & change in potential energy • Potential & equipotential surfaces • Capacitors, capacitance, & voltage drops across capacitors • Millikan oil drop experiment • Excess Charge Distribution on a Conductor

Gravitational Fields: Review Recall that surrounding any object with mass, or collection of objects with mass, is a gravitational field. Any mass placed in a gravitational field will experience a gravitational force. We defined the field strength as the gravitational force per unit mass on any “test mass” placed in the field: g = F / m. g is a vector that points in the direction of the net gravitational force; its units are N / kg. F is the vector force on the test mass, and m is the test mass, a scalar. g and F are always parallel. The strength of the field is independent of the test mass. For example, near Earth’s surface mg / m = g = 9. 8 N / kg for any mass. Some fields are uniform (parallel, equally spaced fields lines). Nonuniform fields are stronger where the field lines are closer together. uniform field 10 kg 98 N Earth’s surface nonuniform field Earth F m

Electric Fields: Intro Surrounding any object with charge, or collection of objects with charge, is a electric field. Any charge placed in an electric field will experience a electrical force. We defined the field strength as the electric force per unit charge on any “test charge” placed in the field: E = F / q. E is a vector that points, by definition, in the direction of the net electric force on a positive charge; its units are N / C. F is the vector force on the test charge, and q is the test charge, a scalar. E and F are only parallel if the test charge is positive. Some fields are uniform (parallel, equally spaced fields lines) such as the field on the left formed by a sheet of negative charge. Nonuniform fields are stronger where the field lines are closer together, such as the field on the right produced by a sphere of negative charge. uniform field +q F - - - - nonuniform field F + q

Overview of Fields Charge, like mass, is an intrinsic property of an object. Charges produce electric fields that affect other charges; masses produce gravitational fields that affect other masses. Gravitational fields lines always point toward an isolated mass. Unlike mass, though, charges can be positive or negative. Electric field lines emanate from positive charges and penetrate into negative charge. We refer to the charge producing a field as a field charge. A group of field charges can produce very nonuniform fields. To determine the strength of the field at a particular point, we place a small, positive test charge in the field. We then measure the electric force on it and divide by the test charge: E = F / q. For an isolated positive field charge, the field lines point away from the field charge (since the force on a positive charge would be away from the field charge). The opposite is true for an isolated negative field charge. No matter how complex the field, the electric force on a test charge is always tangent to the field line at that point. The coming slides will reiterate these ideas and provide examples.

Electric & Gravitational Fields Compared Field strength Force Intrinsic Property SI units Gravity: g = W / m N / kg Electric Force: E = FE / q N/C Field strength is given by per unit mass or force per unit charge, depending on the type of field. Field strength means the magnitude of a field vector. Ex #1: If a +10 C charge is placed in an electric field and experiences a 50 N force, the field strength at the location of the charge is 5 N/C. The electric field vector is given by: E = 5 N/C, where the direction of this vector is parallel to the force vector (and the field lines). Ex #2: If a -10 C charge experiences a 50 N force, E = 5 N/C in a direction opposite the force vector (opposite the direction of the field lines).

Electric Field Example Problem A sphere of mass 1. 3 grams is charged via friction, and in the process excess electrons are rubbed onto it, giving the sphere a charge of - 4. 8 μC. The sphere is then placed into an external uniform electric field of 6 N/C directed to the right. The sphere is released from rest. What is its displacement after 15 s? (Hints on next slide. ) E -

E Sample Problem Hints 1. Draw a vector as shown. Note that FE = q E, by definition of E, and that FE is to the left (opposite E ) since the charge is negative. 2. Instead of finding the net force (which would work), compute the acceleration due to each force separately. q. E mg 3. Find the displacement due to each force using the time given and kinematics. 4. Add the displacement vectors to find the net displacement vector.

Drawing an E Field for a Point Charge Let’s use the idea of a test charge to produce the E field for an isolated positive field charge. We place small, positive test charges in the vicinity of the field and draw the force vector on each. Note that the closer the test charge is to the field charge, the greater the force, but all force vectors are directed radially outward from the field charge. At any point near the field charge, the force vector points in the direction of the electric field. Thus we have a field that looks like a sea urchin, with field lines radiating outward from the field charge to infinity in all direction, not just in a plane. The number of field lines drawn in arbitrary, but they should be evenly spaced around the field charge. What if the field charge were negative? + Test charges and force vectors surrounding a field charge + Isolated, positive point charge and its electric field

Single Positive Field Charge This is a 2 D picture of the field lines that surround a positive field charge that is either point-like or spherically symmetric. Not shown are field lines going out of and into the page. Keep in mind that the field lines radiate outwards because, by definition, an electric field vector points in the direction of the force on a positive test charge. + The nearer you get to the charge, the more uniform and stronger the field. Farther away the field strength gets weaker, as indicated by the field lines becoming more spread out.

Single Negative Field Charge The field surrounding an isolated, negative point (or spherically symmetric) charge looks just like that of an isolated positive charge except the field lines are directed toward the field charge. This is because, by definition, an electric field vector points in the direction of the force on a positive test charge, which, in this case is toward the field charge. As before, the field is stronger where the field lines are closer together, and the force vector on a test charge is parallel to the field. -

Point Charges of Different Magnitudes Let’s compare the fields on two separate isolated point charges, one with a charge of +1 unit, the other with a charge of +2 units. It doesn’t matter how many field lines we draw emanating from the +1 charge so long as we draw twice as many line coming from the +2 charge. This means, at a given distance, the strength of the E field for the +2 charge is twice that for the +1 charge. +1 +2

Equal but Opposite Field Charges Pictured is the electric field produced by two equal but opposite charges. Because the charges are of the same magnitude, the field is symmetric. Note that all the lines that emanate from the positive charge land on the negative charge. Also pictured is a small positive charge placed in the field and the force vector on it at that position. This is the vector sum of the forces exerted on the test charge by each field charge. Note that the net force vector is tangent to the field line. This is always the case. In fact, the field is defined by the direction of net force vectors on test charges at various places. The net force on a negative test charge is tangent to the + field as well, but it points in the opposite direction of the field. (Continued on next slide. ) Link #1 Link #2 Link #3

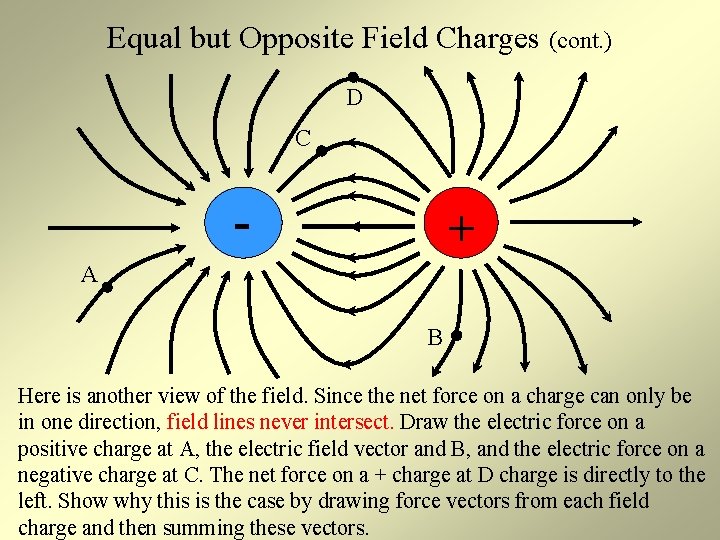
Equal but Opposite Field Charges (cont. ) D C - + A B Here is another view of the field. Since the net force on a charge can only be in one direction, field lines never intersect. Draw the electric force on a positive charge at A, the electric field vector and B, and the electric force on a negative charge at C. The net force on a + charge at D charge is directly to the left. Show why this is the case by drawing force vectors from each field charge and then summing these vectors.

Multiple Charges: How to Determine the Field To determine the field surrounding two field charges, Q 1 and Q 2, we pick some points in the vicinity and place test charges there (red dots). Q 1 exerts a force on each, directly away from itself (blue vectors), as does Q 2 (purple vectors). The resultant vectors (black) show the direction of the net electric force and define the direction of the electric field. The net force vector on each test charge is tangent to the E field there. If we place little a tangent segment parallel with the net force at each test charge and do this at many different points, we will build a picture of the electric field. The same procedure can be used regardless of the number of field charges. Q 1 + Q 2 +

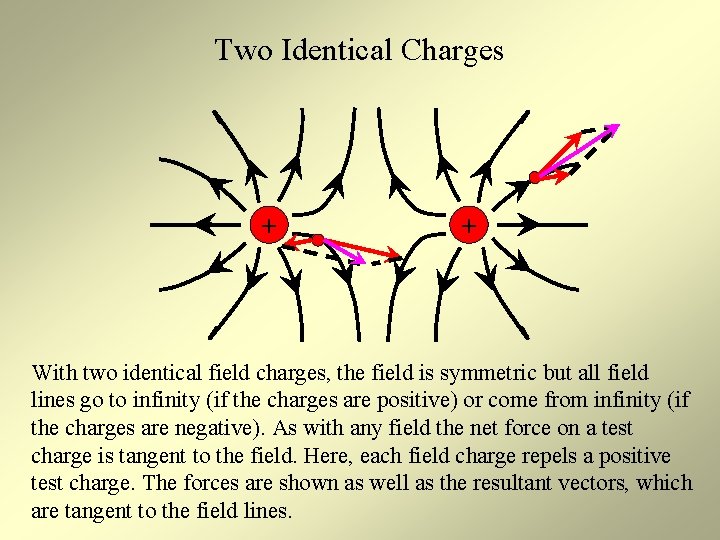
Two Identical Charges + + With two identical field charges, the field is symmetric but all field lines go to infinity (if the charges are positive) or come from infinity (if the charges are negative). As with any field the net force on a test charge is tangent to the field. Here, each field charge repels a positive test charge. The forces are shown as well as the resultant vectors, which are tangent to the field lines.

Coulomb’s Law Review The force that two point charges, Q and q, separated by a distance r, exert on one another is given by: KQq F= 2 r where K = 9 109 Nm 2/C 2 (constant). This formula only applies to point charges or spherically symmetric charges. Suppose that the force two point charges are exerting on one another is F. What is the force when one charge is tripled, the other is doubled, and the distance is cut in half ? Answer: 24 F

Field Strengths: Point Charge; Point Mass Suppose a test charge q is placed in the electric field produced by a point-like field charge Q. From the definition of electric field and Coulomb’s law K Qq / r 2 KQ F E= = = q q r 2 Note that the field strength is independent of the charge placed in it. Suppose a test mass m is placed in the gravitational field produced by a point-like field mass M. From the definition of gravitational field and Newton’s law of universal gravitation GM F G Mm / r 2 g= = = 2 m m r Again, the field strength is independent of the mass place in it.

Uniform Field Just as near Earth’s surface the gravitational field is approximately uniform, the electric field near the surface of a charged sphere is approximately uniform. A common way to produce a uniform E field is with a parallel plate capacitor: two flat, metal, parallel plates, one negative, one positive. Aside from some fringing on the edges, the field is nearly uniform inside. This means everywhere inside the capacitor the field has about the same magnitude and direction. Two positive test charges are depicted along with force vectors. - - + + + +

Two + Field Charges of Different Magnitude • More field lines emanate from the greater charge; none of the field lines cross and they all go to infinity. • The field lines of the greater charge looks more like that of an isolated charge, since it dominates the smaller charge. • If you “zoomed out” on this picture, i. e. , if you looked at the field from a great distance, it would look like that of an isolated point charge due to one combined charge. + + Although in this pic the greater charge is depicted as physically bigger, this need not be the case.

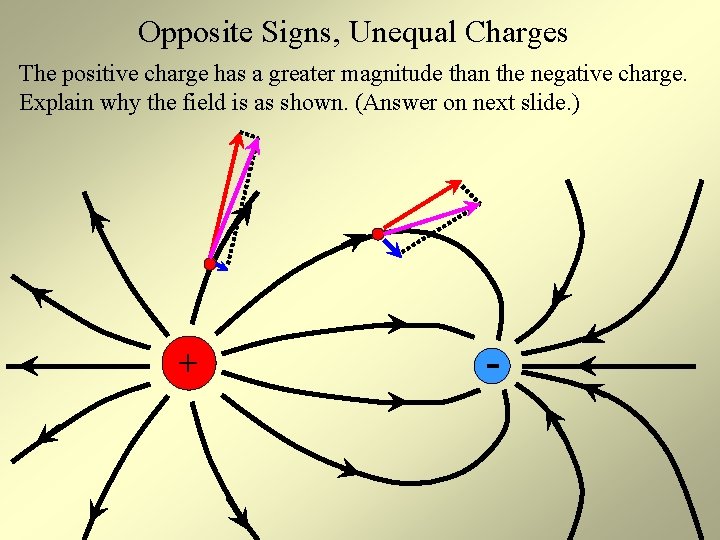
Opposite Signs, Unequal Charges The positive charge has a greater magnitude than the negative charge. Explain why the field is as shown. (Answer on next slide. ) + -

Opposite Signs, Unequal Charges + (cont. ) - More field lines come from the positive charge than land on the negative. Those that don’t land on the negative charge go to infinity. As always, net force on a test charge is the vector sum of the two forces and it’s tangent to the field. Since the positive charge has greater magnitude, it dominates the negative charge, forcing the “turning points” of the point to be closer to the negative charge. If you were to “zoom out” (observe the field from a distance) it would look like that of an isolated, positive point with a charge equal to the net charge of the system.

Summary of Fields due to Unequal Charges You should be able to explain each case in some detail.

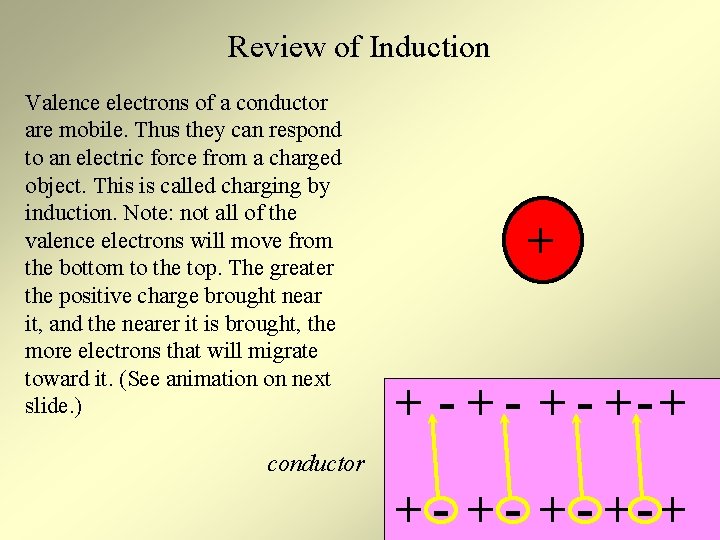
Review of Induction Valence electrons of a conductor are mobile. Thus they can respond to an electric force from a charged object. This is called charging by induction. Note: not all of the valence electrons will move from the bottom to the top. The greater the positive charge brought near it, and the nearer it is brought, the more electrons that will migrate toward it. (See animation on next slide. ) + + - + - +- + conductor + - + - +-+

Review of Induction + (cont. ) Because of the displaced electrons, a charge separation is induced in the conductor. + - + -+ + +

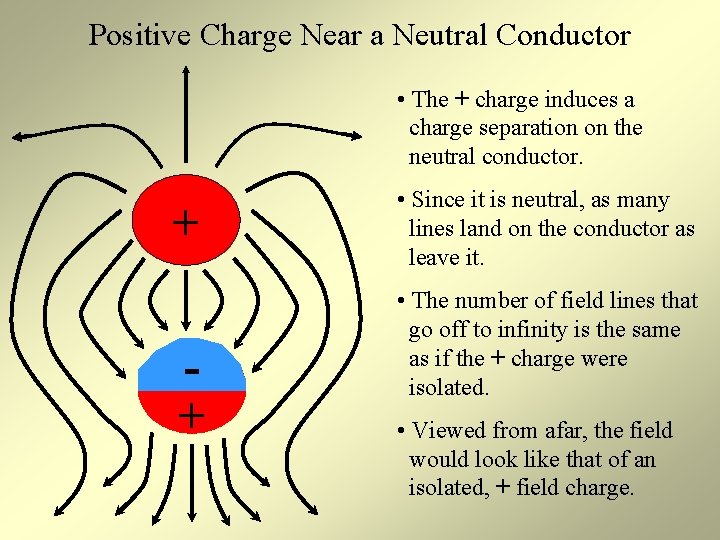
Positive Charge Near a Neutral Conductor • The + charge induces a charge separation on the neutral conductor. + + • Since it is neutral, as many lines land on the conductor as leave it. • The number of field lines that go off to infinity is the same as if the + charge were isolated. • Viewed from afar, the field would look like that of an isolated, + field charge.

Overview of Field Types For the following scenarios, you should be able to draw the associated electric fields correctly: 1. 2. 3. 4. 5. 6. 7. 8. A uniform field An isolated + point charge An isolated – charge Two identical + point charges Two identical – point charges Point charge (either sign) near neutral conductor Unequal point charges of the same sign Unequal point charges of the opposite sign Note that a field drawn without a direction indicated (without arrows) is incorrect. You should be able to draw vector forces on positive or negative charges placed in any field. Also, for complex fields you should be able to describe them as the appear from a distance.

Work done by Fields & Applied Forces To lift an object of mass m a height h in a uniform gravitational field g without acceleration, you must apply a force m g. The work you do is + m g h, while the work done by the field is - m g h. When you lower the object, you do negative work and the field does positive work. Near the surface of a negatively charged object, the electric field is nearly uniform. To lift without acceleration a positive charge q in a downward field E requires a force q E. You do positive work in lifting the charge, and the field does negative work. The signs reverse when you lower the charge. m mg Earth’s surface g E +q q. E Negatively charged surface

Fields: Work & Potential Energy The work your applied force does on the mass or on the charge can go into kinetic energy, waste heat, or potential energy. If there is no friction and no acceleration, then the work you do goes into a change of potential energy: U = m g h for a mass in a gravitational field and U = q E h for a charge in a uniform electric field. The sign of h determines the sign of U. (If a charged object is moved in a vicinity where both types of fields are present, we’d have to use both formulae. ) Whether or not there is friction or acceleration, it is always the case that the work done by the field is the opposite of the change in potential energy: Wfield = - U. m mg Earth’s surface g E +q q. E Negatively charged surface

Work-Energy Example Here the E field is to the right and approximately uniform. The applied force is FA to the left, as is the displacement. The work done by FA is + FA d. The work done by the field is WF = - q E d. The change in electric potential energy is U = - WF = + q E d. Since FA > q E, the applied force does more positive work than the field does negative work. The difference goes into kinetic energy and heat. The work done by friction is Wfric < 0. So, Wnet = FA d - q E d - |Wfric| = K by the work-energy theorem. d + + + FA + + q. E -

Work-Energy Practice For each situation a charge is displaced by some applied force while in a uniform electric field. Determine the sign of: the work done by the applied force; the work done by the field; and U. 1. q is positive and displaced to the right. 2. q is negative and displaced to the right. 3. q is positive and displaced to the left. 4. q is negative and displaced to the left. + + + q -

Potential Gravitational potential is defined to be gravitational potential energy per unit mass. At any given height above Earth’s surface, the gravitational potential is a constant since U / m = m g h / m = g h. Thus potential is independent of mass. If M > m and they’re at the same height, M has more potential energy than m, but they are at the same potential. Similarly, electric potential, V, is defined to be electric potential energy per unit charge. At any given distance from a charged surface in a uniform field, the electric potential is a constant since U / q = q E d / q = E d. Thus potential is independent of charge. If Q > q and they’re the same distance from the surface, Q has more potential energy than q, but they are at the same potential. In a uniform field V = E d. g m E M q h Earth’s surface Q d Negatively charged surface

SI Units for Potential By definition, electric potential is potential energy per unit charge. So, U V= q The SI unit for electric potential is the volts. Both potential and its unit are notated by the capital letter “V. ” Based on the definition above, a volt is defined as joule per coulomb: 1 J 1 V= C Ex: If an object with a 10 C charge is placed at a certain point in an electric field so that its potential energy is 50 J, every coulomb of charge in the object contributes to 5 J of its energy, and its potential is 5 J / C, that is, 5 V.

Equipotential Surfaces As with gravitational potential energy, the reference point for electric potential energy, and hence potential, is arbitrary. Usually what matters is a change in potential, so we just pick a convenient place to call potential energy zero. The dotted lines on the left represent equipotential surfaces--planes in which masses all have the same potential, regardless of the mass. On the 30 J/kg surface, for example, every kilogram of every mass has 30 J of potential energy. Note that equipotentials are always perpendicular to field lines. The equipotentials on the right are labeled in volts. Potential decreases with distance from a positively charged surface since a positive charge loses potential energy as it recedes from the surface. Here again the equipotentials are perpendicular to the field lines. On the -45 V surface, every coulomb of charges has -45 J of potential energy. A -2 C charge there has a potential energy of +90 J. Earth’s surface 40 J / kg -60 V 30 J / kg 20 J / kg 10 J / kg -45 V -30 V -15 V 0 V Positively charged surface

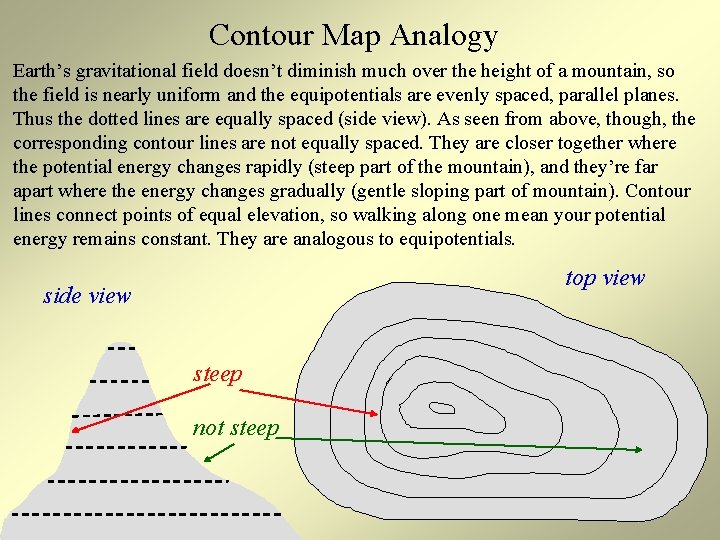
Contour Map Analogy Earth’s gravitational field doesn’t diminish much over the height of a mountain, so the field is nearly uniform and the equipotentials are evenly spaced, parallel planes. Thus the dotted lines are equally spaced (side view). As seen from above, though, the corresponding contour lines are not equally spaced. They are closer together where the potential energy changes rapidly (steep part of the mountain), and they’re far apart where the energy changes gradually (gentle sloping part of mountain). Contour lines connect points of equal elevation, so walking along one mean your potential energy remains constant. They are analogous to equipotentials. top view side view steep not steep

Equipotential Surfaces: Positive Point Charge Imagine a positive test charge, q, approaching an isolated, positive, point-like field charge, Q. The closer q approaches, the more potential energy it has. So, potential increases as distance decreases. Next year we’ll derive this formula for potential due to a point charge: V = KQ / r. This shows that V is proportional to Q, that V → 0 as r → ∞, and that V → ∞ as r → 0. Equipotential surfaces are always perpendicular to the field lines, for any charge configuration. For a point charge the surfaces are spheres centered at Q. Here the surfaces could be labeled from the inside out: 100 V, 90 V, 80 V, and 70 V. Every 10 V step is bigger than the previous, since the field + is getting weaker with distance. The gap between the 50 V and 40 V surfaces would be very large, and the gap between 10 V and 0 V would be infinite.

Equipotential Surfaces: Negative Point Charge The field and the equipotentials look just like that of the isolated, positive point charge. However, the field lines point in the opposite direction and the potential decreases with distance. Imagine a positive test charge, q, approaching an isolated, negative, point-like field charge, -Q. The closer q approaches, the more negative its potential energy becomes. So, V → 0 as r → ∞ (as with the positive field charge), but V → - ∞ as r → 0. Here the surfaces could be labeled from the inside out: -100 V, -90 V, -80 V, and -70 V. Every 10 V step is bigger than the previous, since V = zero at infinity. (The step size to be drawn is a matter of choice. ) A +3 C charge placed on the -70 V surface has a potential energy of -210 J.

Equipotentials Surfaces for Multiple-charge Configurations In class practice: First experiment with the link, then draw equipotentials on the board on top of this picture. Here are the rules: Link • Equipotentials are always perpendicular to the field lines. • Equipotentials never intersect one another. • The potential is large & positive near a positive charge, large & negative near a negative charge, and near zero far from all the charges. • Equipotentials are close together where potential energy changes quickly (close to charges). + -

Moving in an Electric Field 80 V 90 0 V 10 Electric and gravitation fields are called conservative fields because, when a mass/charge moves about one, any change in potential energy is independent of path. A charge taking a straight-line path from A to B undergoes a change in potential of 10 V ( V = +10 V). If a charge takes the long, curvy path, its energy increases as it approaches the field charge, and D decreases as it recedes, but the change is the same as the straight-line path. In either case each coulomb of C charge gains 10 J of potential energy. A B No matter what path is taken: VC→A = -20 V, and VD→A = 0. + V is independent of path! From A to D along the equipotential the field can do no work, since the displacement if always to E, which is || to F. Recall: W = F · x = F x cos. V 70 V

Capacitors - Overview • A capacitor is a device that stores electrical charge. • A charged capacitor is actually neutral overall, but it maintains a charge separation. • The charge storing capacity of a capacitor is called its capacitance. • An electric field exists inside a charged capacitor, between the positive and negative charge separation. • A charged capacitor store electrical potential energy. • Capacitors are ubiquitous in electrical devices. They’re used in power transmission, computer memory, photoflash units in cameras, tuners for radios and TV’s, defibrillators, etc.

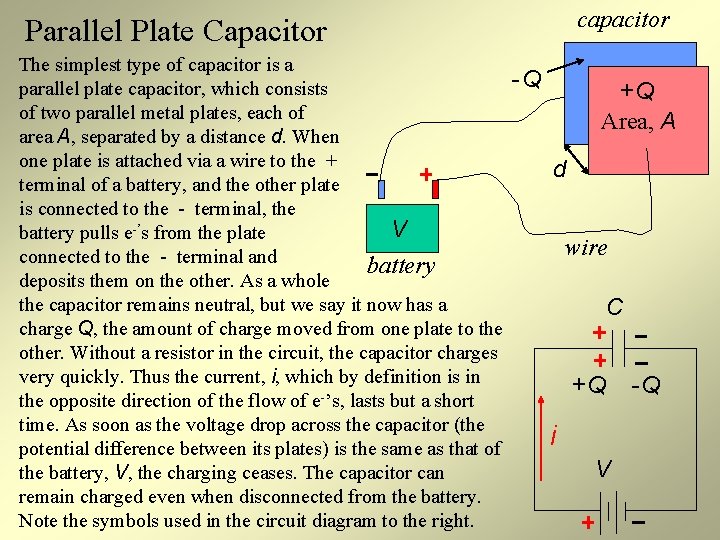
capacitor Parallel Plate Capacitor The simplest type of capacitor is a parallel plate capacitor, which consists of two parallel metal plates, each of area A, separated by a distance d. When one plate is attached via a wire to the + terminal of a battery, and the other plate is connected to the - terminal, the V battery pulls e-’s from the plate connected to the - terminal and battery deposits them on the other. As a whole the capacitor remains neutral, but we say it now has a charge Q, the amount of charge moved from one plate to the other. Without a resistor in the circuit, the capacitor charges very quickly. Thus the current, i, which by definition is in the opposite direction of the flow of e-’s, lasts but a short time. As soon as the voltage drop across the capacitor (the potential difference between its plates) is the same as that of the battery, V, the charging ceases. The capacitor can remain charged even when disconnected from the battery. Note the symbols used in the circuit diagram to the right. -Q +Q Area, A d wire C +Q i V -Q

Parallel Plate Capacitor: E & U Because of the charge separation, an electric field exists between the plates of a charged capacitor. If it is a parallel plate variety, the field is very nearly uniform inside, with some fringing on the edges, as we’ve seen before. Outside the plates the field is very weak. The strength of the E field inside is proportional to how much charge is on the capacitor and inversely proportional to how the capacitors area. (Less area means the charge is more concentrated and the field is stronger. ) A charged capacitor also stores potential energy (in an amount proportional to the square of the charge) since energy is required to separate the charges in the first place. Touching a charged capacitor will allow it to discharge quickly and will result in a shock. Once discharged, the electric field vanishes and the potential energy is converted to some other form. - - + + + +

Capacitance, C, is the capacity to store charge. The amount of charge, Q, stored on given capacitor depends on the potential difference between its plates, V, and its capacitance C. In other words, Q is directly proportional to V, and the constant of proportionality is C: Q = CV Ex: A 12 V battery will cause a capacitor to store twice as much charge as a 6 V battery. Also, if capacitor #2 has twice the capacitance of capacitor #1, then #2 will store twice as much charge as #1, provided they are charged by the same battery. C depends on the type of the capacitor. For a parallel plate capacitor, C is proportional to the area, A and inversely proportional to the plate separation, d. C Q V

Capacitance: SI Units The SI unit for capacitance is the farad, named for the famous 19 th century scientist Michael Faraday. Its symbol is F. From the defining equation for capacitance, Q = CV, we define a farad: implies Q = CV 1 C = (1 F) (1 V) So, a farad is a coulomb per volt. This means a capacitor with a capacitance of 3 F could store 30 C of charge if connected to a 10 V battery. This is a tremendous amount of charge for a reasonable potential difference. Thus a farad is a large amount of capacitance. Many capacitors have capacitances measured in p. F or f. F (pico or femtofarads). m: milli = 10 -3, μ: micro = 10 -6, p: pico = 10 -12, n: nano = 10 -9, f: femto = 10 -15

Capacitance Problem A parallel plate capacitor is fully charged by a 20 V battery, acquiring a charge of 1. 62 n. C. The area of each plate is 3. 5 cm 2 and the gap between them is 1. 3 mm. What is the capacitance of the capacitor? From Q = C V, C = Q / V = (1. 62 10 -9 C) / (20 V) = 8. 1 10 -11 F = 81 10 -12 F = 81 p. F. The gap and area are extraneous. - 1. 62 μC + 1. 62 μC 3. 5 cm 2 1. 3 mm 20 V

V = Ed As argued on the slide entitled “Potential, ” in a uniform field, V = E d. This argument was based on an analogy with gravity and applies only to uniform fields: gravitational: U = m g h electric: U = q E d U / q = E d V = E d Since E is uniform inside a parallel plate capacitor, the voltage drop across it is equal to the magnitude of the electric field times the distance between the plates. d

V = E d (formal derivation) U V= q (from the definition of potential) |Wfield | V= q (since Wfield = - U ) Fd V= q (since W = F d ) V= E d F ) (since E = q

Millikan’s Oil Drop Experiment In 1909, Robert Millikan performed an experiment to determine the charge of an electron. The charge to mass ratio of the electron had already been calculated by J. J. Thomson (discoverer of the electron) in 1897. But until Millikan’s experiment, neither the mass nor the charge was known, only the ratio. By examining the motion of the oil droplets falling between two highly charged plates, he found the charge to be -1. 6 10 -19 C. The charged plates were similar to that of a parallel plate capacitor.

Millikan Apparatus and Experiment A battery connected to the plates kept the top (positive) plate at a higher potential than the lower (negative) plate. So, a nearly uniform, downward E field existed between the plates. An atomizer sprayed tiny oil droplets (of radii about 1 μm) from above the plates, some of which fell through a hole in the positive plate into the E field. Due to friction during the spraying, some of the drops were charged, either positively or negatively. A negatively charged drop that makes it into the hole will not undergo free fall, since it experiences an upward electric force between the plates. The radius, mass, and charge of the drops varied, but by adjusting the potential difference across the plates, Millikan could make a drop hover. Continued… switch

Oil Drop Experiment (cont. ) A drop suspended in midair has no net force on it. This means the downward weight, m g, was negated by an upward electric force, q E. Millikan could vary E by adjusting the potential difference across the plates (V = E d). So, the excess charge on the drop is: q = m g / E = m g d / V. But m needed to be calculated in order to determine q. To find the drop’s mass, he turned off the electric field by opening the switch and disconnecting the battery. The drop then began to fall, but it quickly reached terminal velocity in the air. The greater the falling speed, the greater the drag force, and by measuring terminal speeds, Millikan could calculate the mass. Continued… q. E mg switch d

Oil Drop Experiment (cont. ) At this point Millikan could calculate the charge on a drop. But without knowing the number of excess electrons on the drop, he couldn’t determine the charge of an electron. So, he altered the charge on the drop with X-rays (not shown). The X-rays ionized the surrounding air, which, in turn, altered the charge on the drops. The drops were now no longer in equilibrium, so Millikan adjusted the E field until equilibrium was reestablished. Since at equilibrium q = mgd / V, and all quantities on the right side of the equation were known, Millikan could repeat this X-ray procedure numerous times and calculate the many different charges that a drop could attain. He found that the charge on a drop was always a multiple of 1. 6 10 -19 C. As you know, we now call this amount of charge e, the elementary charge. His experiment showed that charge is quantized, existing in discrete bundles (in this case, electrons) and that the charge on an electron is -1. 6 10 -19 C.

Excess Charge on a Conductor Any excess charge placed on a conductor will immediately distribute itself over the surface of the conductor. No excess charge will remain inside. On a spherical conductor the excess charge will be distributed evenly. If electrons are added, they themselves will spread out. If electrons are removed, electrons in the conductor will replace them, leaving all excess positive charge on the surface. Excess charge placed on an insulator pretty much stays put. + + _ _ + _ + __ _ Now lets add some extra charges. The new charges repel themselves and reside only on the surface.

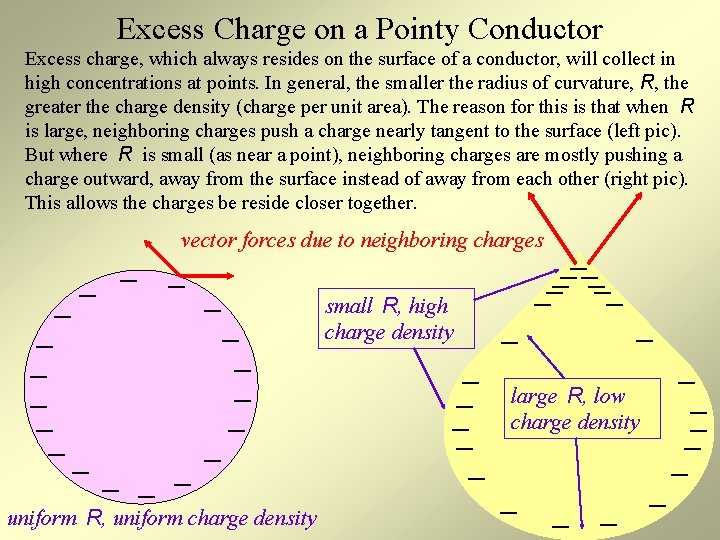
Excess Charge on a Pointy Conductor Excess charge, which always resides on the surface of a conductor, will collect in high concentrations at points. In general, the smaller the radius of curvature, R, the greater the charge density (charge per unit area). The reason for this is that when R is large, neighboring charges push a charge nearly tangent to the surface (left pic). But where R is small (as near a point), neighboring charges are mostly pushing a charge outward, away from the surface instead of away from each other (right pic). This allows the charges be reside closer together. _ _ _ _ _ vector forces due to neighboring charges _ _ _ _ _ uniform R, uniform charge density small R, high charge density _ _ __ _ _ large R, low charge density _ _ _ _ _

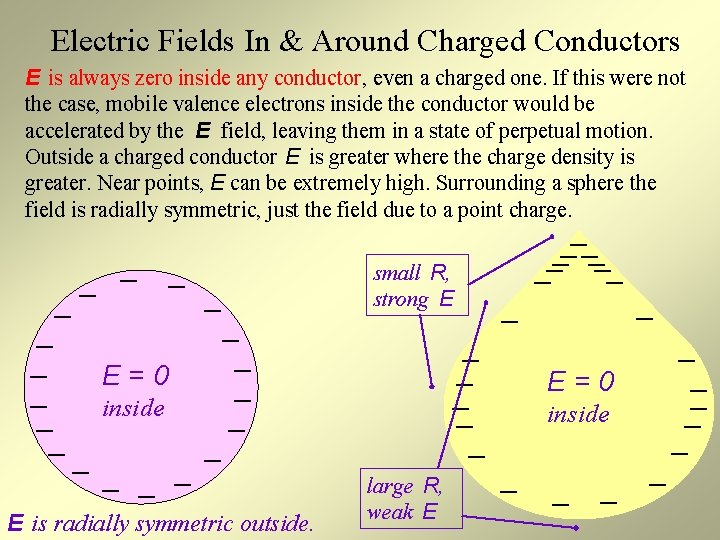
Electric Fields In & Around Charged Conductors E is always zero inside any conductor, even a charged one. If this were not the case, mobile valence electrons inside the conductor would be accelerated by the E field, leaving them in a state of perpetual motion. Outside a charged conductor E is greater where the charge density is greater. Near points, E can be extremely high. Surrounding a sphere the field is radially symmetric, just the field due to a point charge. _ _ _ _ _ E=0 inside _ _ _ _ _ E is radially symmetric outside. small R, strong E _ _ _ large R, weak E __ _ _ E=0 inside _ _ _ _ _

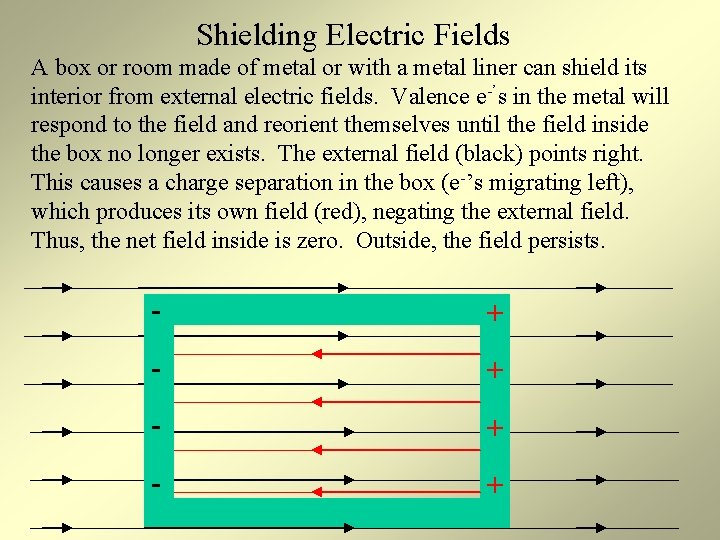
Shielding Electric Fields A box or room made of metal or with a metal liner can shield its interior from external electric fields. Valence e-’s in the metal will respond to the field and reorient themselves until the field inside the box no longer exists. The external field (black) points right. This causes a charge separation in the box (e-’s migrating left), which produces its own field (red), negating the external field. Thus, the net field inside is zero. Outside, the field persists. - + - +

Credits http: //images. google. com/imgres? imgurl=http: //buphy. bu. edu/~duffy/PY 106/2 e. GIF&imgrefurl=http: //physics. bu. edu /~duffy/PY 106/Electricfield. html&h=221&w=370&sz=4&tbnid=y 0 qny 4 b 133 k. J: &tbnh=70&tbnw=117&start=3&pre v=/images%3 Fq%3 Delectric%2 Bfield%26 hl%3 Den%26 lr%3 D Spark Picture: http: //cdcollura. tripod. com/tcspark 2. htm electric field lines: http: //www. gel. ulaval. ca/~mbusque/elec/main_e. html java, placing and moving test charges and regular charges: http: //www. physicslessons. com/exp 21 b. htm java animation, placing test charges: http: //www. colorado. edu/physics/2000/waves_particles/wavpart 3. html http: //www. slcc. edu/schools/hum_sci/physics/tutor/2220/e_fields/ lesson, pictures, units: http: //www. pa. msu. edu/courses/1997 spring/PHY 232/lectures/efields/ java electric field: http: //www. msu. edu/user/brechtjo/physics/e. Field. html lesson with animations, explanations: http: //www. cyberclassrooms. net/~pschweiger/field. html http: //library. thinkquest. org/10796/ch 12. htm Robert Millikan: http: //www. nobel. se/physics/laureates/1923/millikan-bio. html Millikan Oil Drop: http: //www. mdclearhills. ab. ca/millikan/experiment. html http: //www. glenbrook. k 12. il. us/gbssci/phys/Class/estatics/u 8 l 4 c 16. gif http: //www. physchem. co. za/Static%20 Electricity/Graphics/GRDA 0008. gif http: //www. eng. uct. ac. za/~victor/electric/charge_opposite_particles. gif