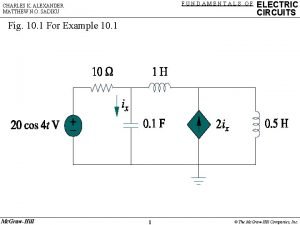
Electric Circuits EELE 2312 Chapter 8 Introduction to



































- Slides: 48

Electric Circuits (EELE 2312) Chapter 8 Introduction to the Laplace Transform Basil Hamed

Introduction • We now introduce a powerful analytical technique that is widely used to study the behavior of linear, • • lumped-parameter circuits. The method is based on the Laplace transform, which we define mathematically in next Section. Before doing so, we need to explain why another analytical technique is needed. First, we wish to consider the transient behavior of circuits whose describing equations consist of more than a single node-voltage or mesh current differential equation. In other words, we want to consider multiple-node and multiple-mesh circuits that are described by sets of linear differential equations. Second, we wish to determine the transient response of circuits whose signal sources vary in ways more complicated than the simple dc level jumps considered in Chapter 7 Third, we can use the Laplace transform to introduce the concept of the transfer function as a tool for analyzing the steady-state sinusoidal response of a circuit when the frequency of the sinusoidal source is varied. Finally, we wish to relate, in a systematic fashion, the time domain behavior of a circuit to its frequency-domain behavior. Using the Laplace transform will provide a broader understanding of Basil Hamed 2 circuit functions.

Introduction In this chapter, we introduce the Laplace transform, discuss its pertinent characteristics, and present a systematic method for transforming from the frequency domain to the time domain. Basil Hamed 3

8. 1 Definition of the Laplace Transform Basil Hamed 4

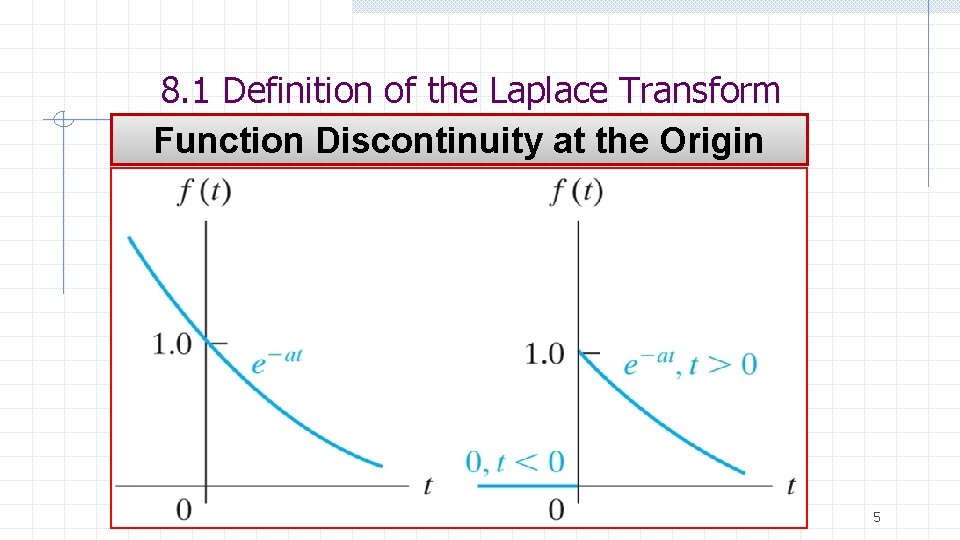
8. 1 Definition of the Laplace Transform Function Discontinuity at the Origin Basil Hamed 5

8. 1 Definition of the Laplace Transform if f(t) has discontinuity and not defined at the origin we designate 0 - and 0+ and exclude f(t) for t<0 values of f(t) for t<0 - are accounted for by initial conditions transform is divided into functional and operational Basil Hamed 6

8. 1 Definition of the Laplace Transform Basil Hamed 7

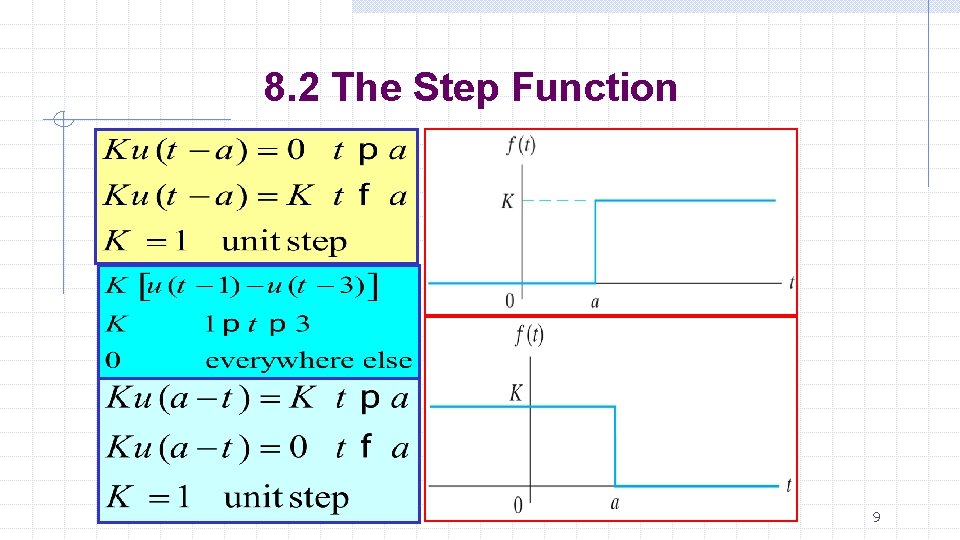
8. 2 The Step Function Basil Hamed 8

8. 2 The Step Function Basil Hamed 9

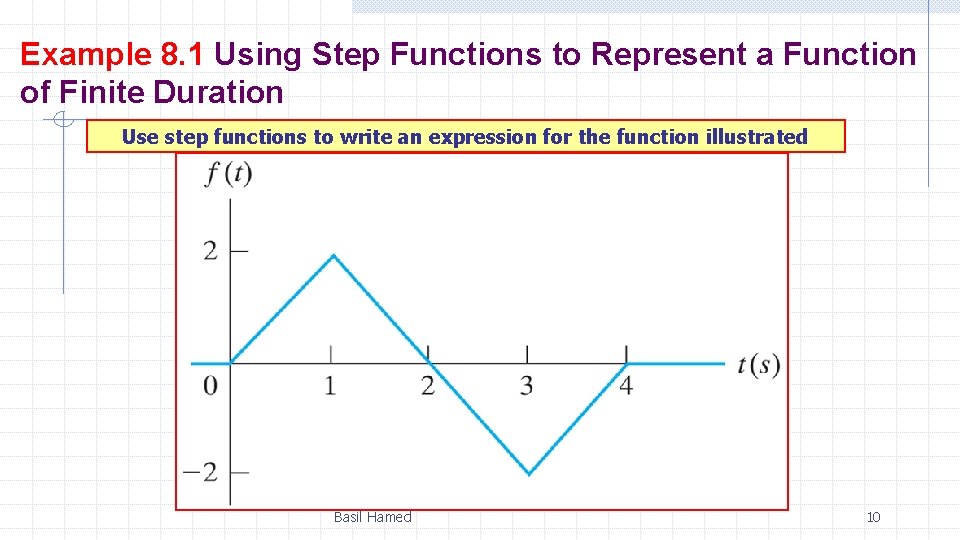
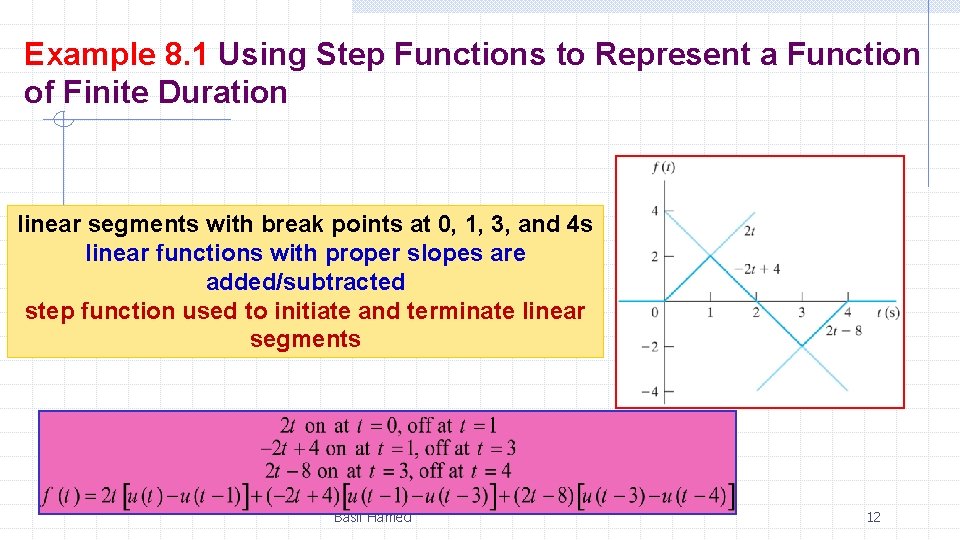
Example 8. 1 Using Step Functions to Represent a Function of Finite Duration Use step functions to write an expression for the function illustrated Basil Hamed 10

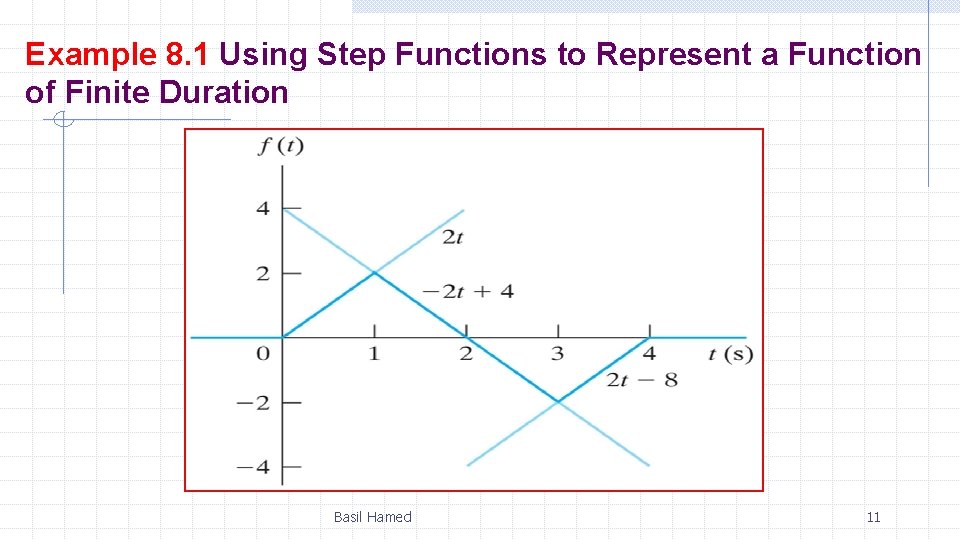
Example 8. 1 Using Step Functions to Represent a Function of Finite Duration Basil Hamed 11

Example 8. 1 Using Step Functions to Represent a Function of Finite Duration linear segments with break points at 0, 1, 3, and 4 s linear functions with proper slopes are added/subtracted step function used to initiate and terminate linear segments Basil Hamed 12

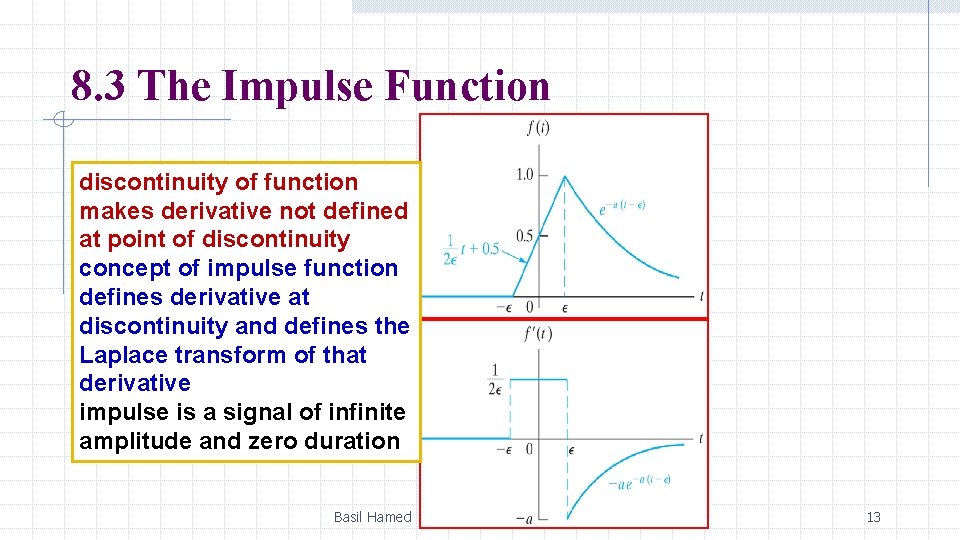
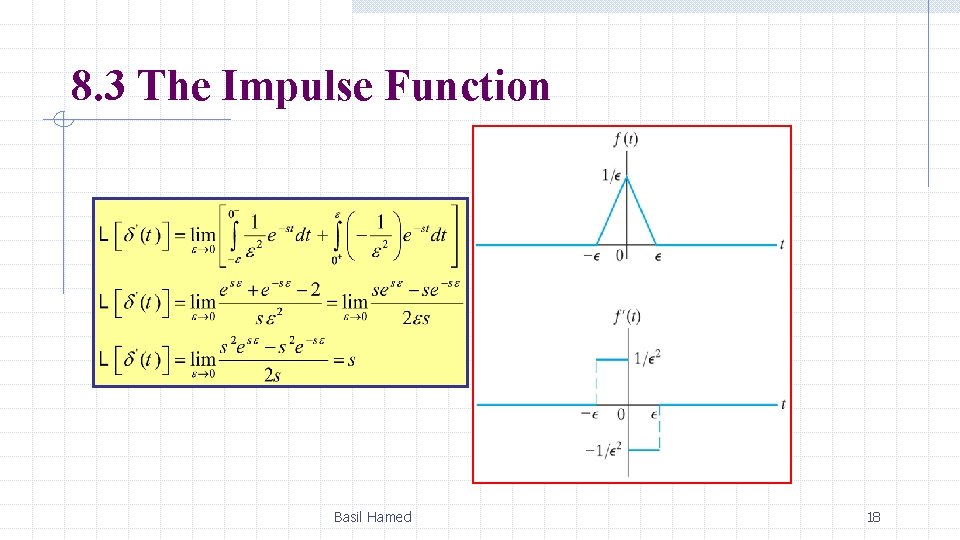
8. 3 The Impulse Function discontinuity of function makes derivative not defined at point of discontinuity concept of impulse function defines derivative at discontinuity and defines the Laplace transform of that derivative impulse is a signal of infinite amplitude and zero duration Basil Hamed 13

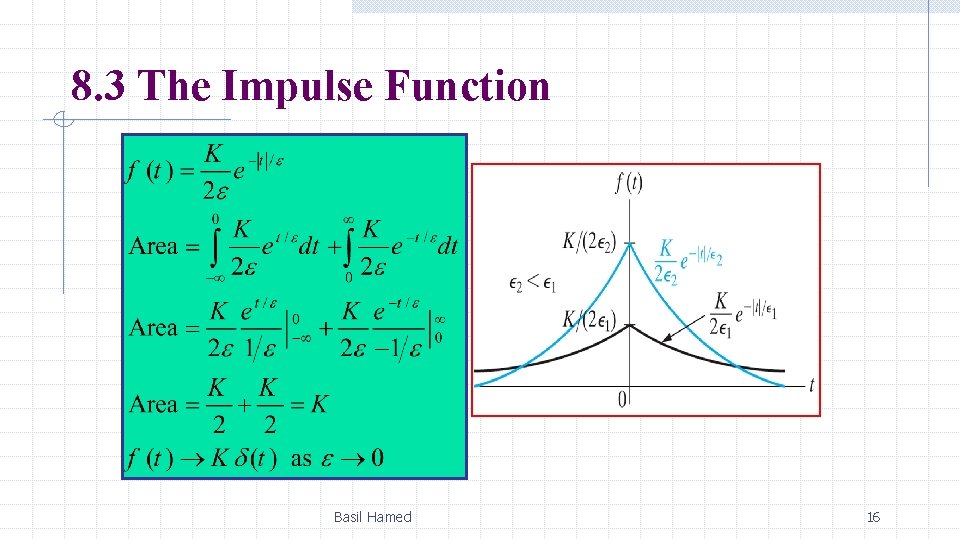
8. 3 The Impulse Function To summarize, an impulse function is created from a variable-parameter function whose parameter approaches zero. The variable-parameter function must exhibit the following three characteristics as the parameter approaches zero: 1. The amplitude approaches infinity. 2. The duration of the function approaches zero. 3. The area under the variable-parameter function is constant as the parameter changes. Basil Hamed 14

8. 3 The Impulse Function the linear function f(t)=0. 5 t/ε+0. 5 satisfies unit impulse properties as ε approaches zero, function between ±ε approaches a unit impulse function δ(t) derivative of f(t) at the origin approaches unit impulse function f’(0)→ δ(t) as ε → 0 If area under curve is other than unity, amplitude is denoted Kδ(t), where K area or strength Basil Hamed 15

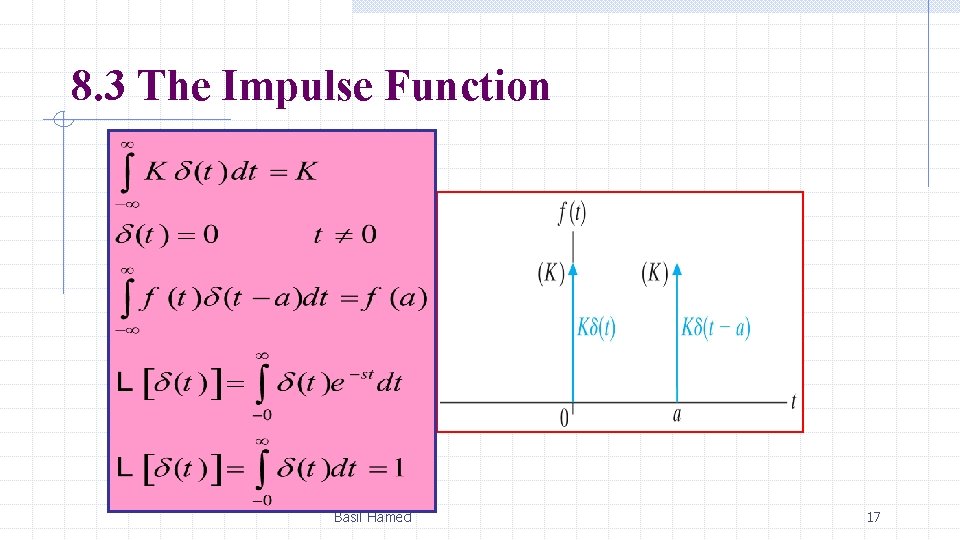
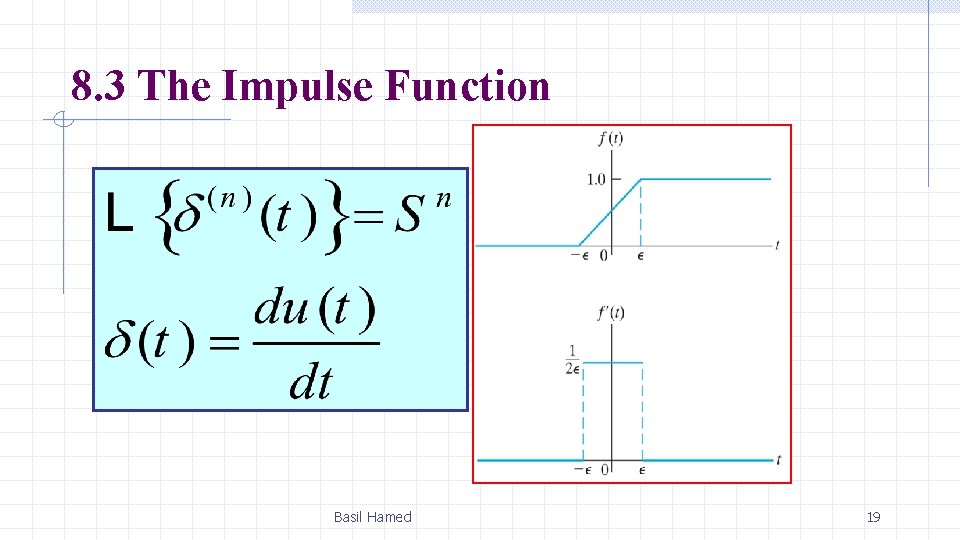
8. 3 The Impulse Function Basil Hamed 16

8. 3 The Impulse Function Basil Hamed 17

8. 3 The Impulse Function Basil Hamed 18

8. 3 The Impulse Function Basil Hamed 19

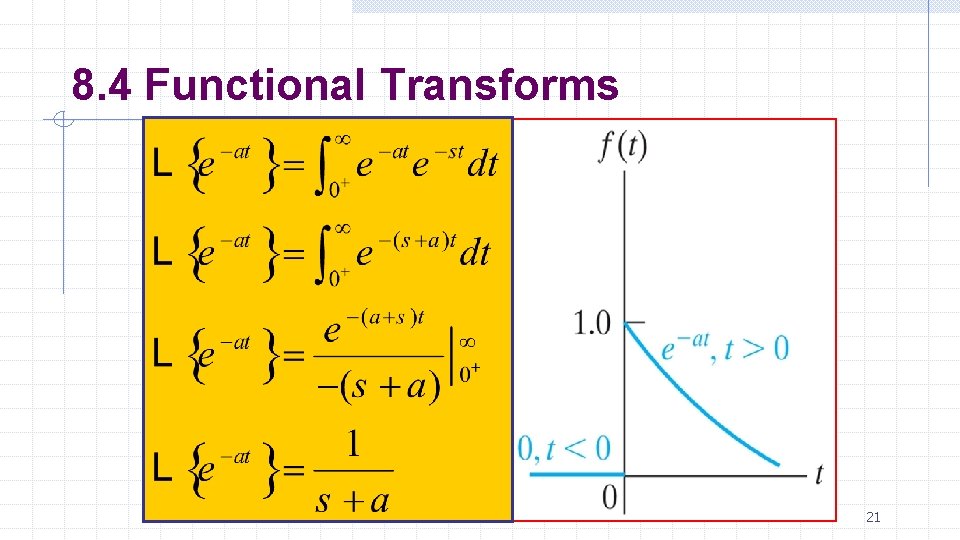
8. 4 Functional Transforms Basil Hamed 20

8. 4 Functional Transforms Basil Hamed 21

8. 4 Functional Transforms Basil Hamed 22

8. 4 Functional Transforms Basil Hamed 23

8. 5 Operational Transforms Operational transforms indicate how mathematical operations performed on either f(t) or F{s) are converted into the opposite domain. The operations of primary interest are (1) multiplication by a constant; (2) addition (subtraction); (3) differentiation; (4) integration; (5) translation in the time domain; (6) translation in the frequency domain; and (7) scale changing. Basil Hamed 24

8. 5 Operational Transform Multiplying by a constant 25

8. 5 Operational Transform Addition and Subtraction 26

8. 5 Operational Transform Differentiation 27

8. 5 Operational Transform Integration 28

8. 5 Operational Transform Translation in the Time Domain 29

8. 5 Operational Transform Translation in the Frequency Domain 30

8. 5 Operational Transform Scale Changing 31

8. 5 Operational Transform Abbreviated List 32

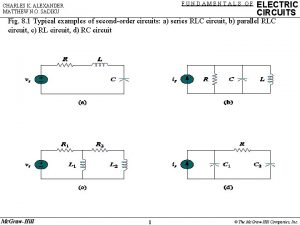
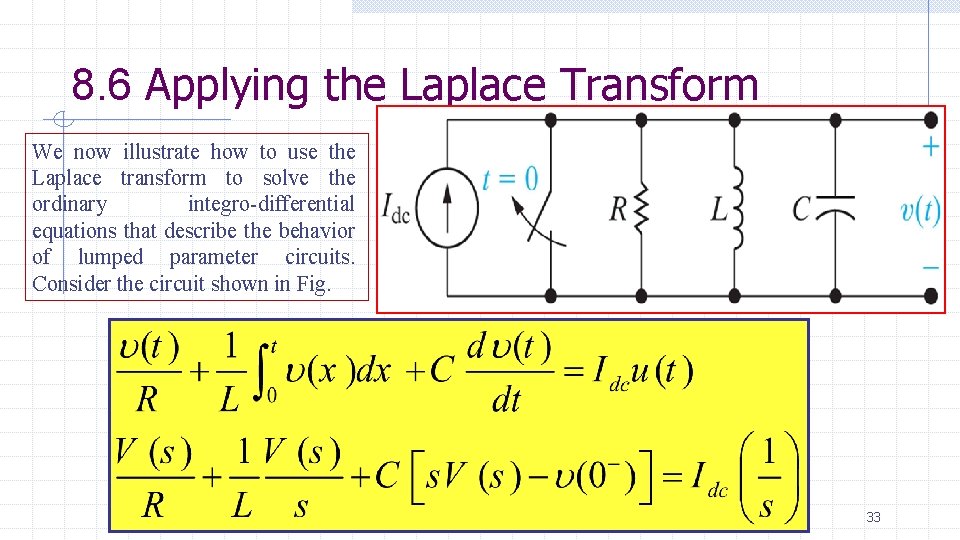
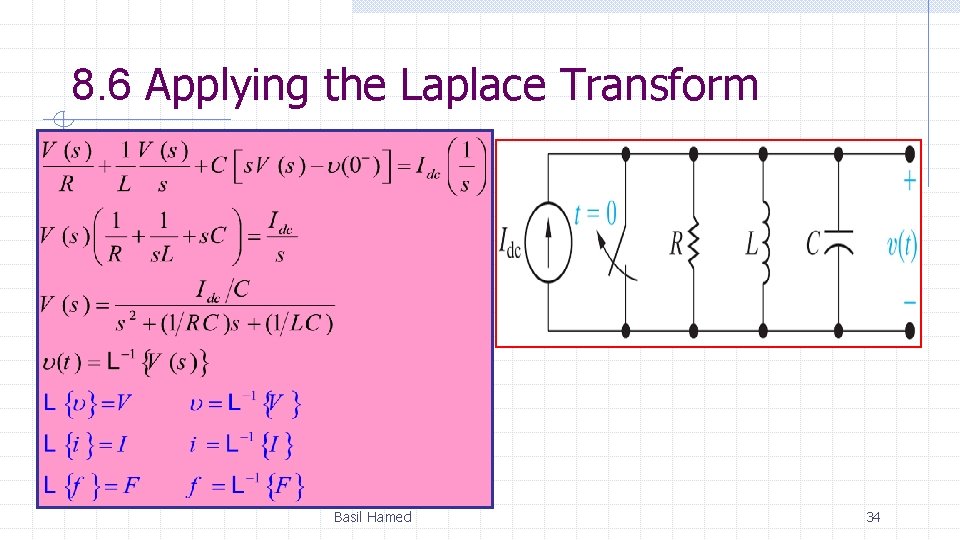
8. 6 Applying the Laplace Transform We now illustrate how to use the Laplace transform to solve the ordinary integro-differential equations that describe the behavior of lumped parameter circuits. Consider the circuit shown in Fig. Basil Hamed 33

8. 6 Applying the Laplace Transform Basil Hamed 34

8. 7 Inverse Transforms The expression for V(s) in Eq. 12. 40 is a rational function of s; that is, one that can be expressed in the form of a ratio of two polynomials in s such that no nonintegral powers of 5 appear in the polynomials. In fact, for linear, lumpedparameter circuits whose component values are constant, the s-domain expressions for the unknown voltages and currents are always rational functions of s. The purpose of this section is to present a straight-forward and systematic technique for finding the inverse transform of a rational function. Basil Hamed 35

8. 7 Inverse Transform 36

8. 7 Inverse Transform Partial Fraction Expansion: Proper Rational Function 37

8. 7 Inverse Transform Partial Fraction Expansion: Distinct Real Roots of D(s) 38

8. 7 Inverse Transform Partial Fraction Expansion: Distinct Complex Roots of D(s) 39

8. 7 Inverse Transform Partial Fraction Expansion: Repeated Real Roots of D(s) 40

8. 7 Inverse Transform Partial Fraction Expansion: Repeated Complex Roots of D(s) 41

Useful Transforms 42

8. 7 Inverse Transform Partial Fraction Expansion: Improper Rational Function 43

8. 8 Poles and Zeros of F(s) 44

8. 9 The Initial- & Final-Value Theorems The initial- and final-value theorems are useful because they enable us to determine from F(s) the behavior of f (t) at 0 and oo. Hence we can check the initial and final values of f (t) to see if they conform with known circuit behavior, before actually finding the inverse transform of F(s). 45

8. 9 The Initial- & Final-Value Theorems 46

8. 9 The Initial- & Final-Value Theorems The Application 47

End Of Chapter Eight 48
 Characteristic impedance definition
Characteristic impedance definition Jonathan eele
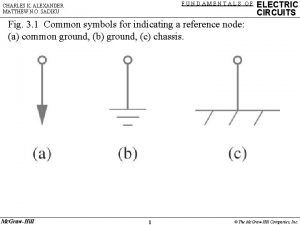
Jonathan eele Introduction to electric circuits
Introduction to electric circuits Find vx
Find vx Introduction to electric circuits
Introduction to electric circuits Cse 2312
Cse 2312 Cse 2312
Cse 2312 Mpu 3313 health and wellness
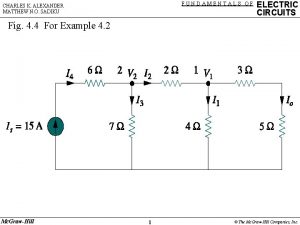
Mpu 3313 health and wellness Fundamentals of electric circuits chapter 4 solutions
Fundamentals of electric circuits chapter 4 solutions Electric current
Electric current Conceptual physics chapter 35
Conceptual physics chapter 35 Chapter 20 electric circuits
Chapter 20 electric circuits Fundamentals of electric circuits chapter 9 solutions
Fundamentals of electric circuits chapter 9 solutions Fundamentals of electric circuits chapter 7 solutions
Fundamentals of electric circuits chapter 7 solutions Chapter 35 electric circuits answers
Chapter 35 electric circuits answers Ohm's law worksheet
Ohm's law worksheet Chapter 35 electric circuits
Chapter 35 electric circuits Advantages of parallel circuits over series circuit
Advantages of parallel circuits over series circuit Chapter 21 electric charge and electric field
Chapter 21 electric charge and electric field Chapter 21 electric charge and electric field
Chapter 21 electric charge and electric field K constant unit
K constant unit Units of a charge
Units of a charge Phet ac circuit
Phet ac circuit Electric circuits equations
Electric circuits equations Electric circuits nilsson
Electric circuits nilsson Principle of electric circuit
Principle of electric circuit Electrical circuit elements
Electrical circuit elements Charles k. alexander matthew n. o. sadiku
Charles k. alexander matthew n. o. sadiku Sadiku
Sadiku Superposition electric circuits
Superposition electric circuits Kshamta hunter
Kshamta hunter Charles k. alexander matthew n. o. sadiku
Charles k. alexander matthew n. o. sadiku Alexander
Alexander The circuit chapter 8 summary
The circuit chapter 8 summary Electric circuits fundamentals floyd
Electric circuits fundamentals floyd Physics reference table
Physics reference table Fundamentals of electric circuits
Fundamentals of electric circuits Alexander
Alexander Quarturs
Quarturs Analogy between electric and magnetic circuits
Analogy between electric and magnetic circuits Capacitance
Capacitance Potential of conductor
Potential of conductor Electric potential energy definition
Electric potential energy definition Electric potential is
Electric potential is A suitable electric pump in an electric circuit is a
A suitable electric pump in an electric circuit is a Electric charges and electric forces lesson outline
Electric charges and electric forces lesson outline D flip flop truth table
D flip flop truth table Nccer introduction to electrical circuits
Nccer introduction to electrical circuits Chapter 23 series and parallel circuits study guide answers
Chapter 23 series and parallel circuits study guide answers