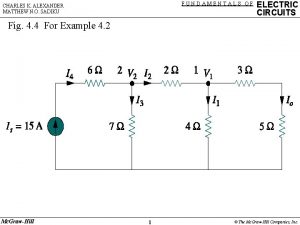
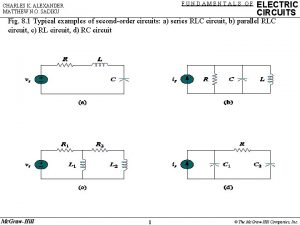
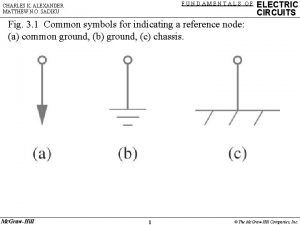
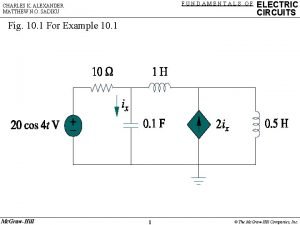
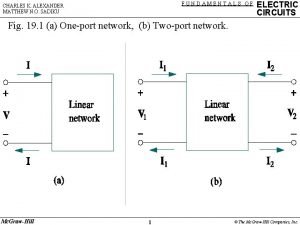
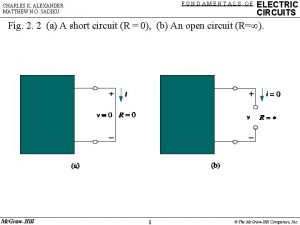
Fundamentals of Electric Circuits Chapter 18 Copyright The

Fundamentals of Electric Circuits Chapter 18 Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

Overview • In this chapter, the Fourier series is extended to cover no-repeating signals. • The concept of the Fourier transform: a function that converts a signal from time domain to frequency domain is introduced. • The inverse transform, which converts from frequency to time domain is also introduced. • Properties of the transform are covered. • Finally, a comparison between the Laplace and Fourier transforms will be made. 2

Non Periodic Functions • We have seen how Fourier series can represent any periodic waveform. • But, many signals of interest in electronics are not periodic. • Although these cannot be represented in a Fourier series, they can be transformed into frequency domain by use of something called the Fourier transform. 3

Stretching the Period • One way to consider a nonperiodic function is to take a periodic one and stretch the period. • Consider the periodic function shown at the bottom of the figure. • If the period T→ , then the function becomes non-periodic. 4

Effect on the Spectrum • Here you can see the impact of increasing the period has. • As the pulses are spaced out more, the peaks in the frequency spectrum get closer together • The amplitude also drops. 5

Effect on the Spectrum II • Note that the sum of the amplitudes does not change. • Ultimately what will happen is as the period goes to infinity, the discrete spectrum will become a continuous spectrum. • The result is what is known as the Fourier transform 6

Inverse Fourier • The Fourier transform is an integral transform of f(t) from the time domain to the frequency domain. • In general, F(ω) is a complex function. • Its magnitude is called the amplitude spectrum. • The phase is called the phase spectrum. • There is also a inverse transform: 7

Conditions on F(ω) • The Fourier transform does not exist for all functions. • It only exists where the Fourier integral converges. • A sufficient, but not necessary condition is: • An example of a function that would fail this test is the unit ramp function. 8

Example 1 Determine the Fourier transform of a single rectangular pulse of wide t and height A, as shown below. A rectangular pulse 9

Solution: Amplitude spectrum of the rectangular pulse 10

Example 2: Obtain the Fourier transform of the “switched-on” exponential function as shown below. 11

Solution: 12

Linearity of F(ω) • We will now establish some of properties of the Fourier transform • Linearity: If F 1(ω) and F 2(ω) are the Fourier transforms of f 1(t) and f 2(t) then • Where a 1 and a 2 are constants. • This simply states that the transform of a linear combination of functions equals the linear combination of each transform. 13

Time Scaling • In time scaling: • This shows that time expansion (|a|>1) corresponds to frequency compression and vice versa. • In other words, imagine a pulse that becomes shorter; the Fourier transform of this broadens in frequency. 14

Time Scaling II • The effect of time scaling can be seen in this example: 15

Frequency Shifting • In frequency shifting: • A frequency shift in the frequency domain adds a phase shift to the time function. • This can also be seen as amplitude modulation in the time domain. • This has important consequences for modulation, a common form of communication. 16

17

18

Time Differentiation • In time differentiation: • The transform of the derivative of f (t) is obtained by multiplying the transform of f (t) by jω. • This can be generalized to the n’th derivative: 19

Time Integration • In time integration: • the transform of the integral of f (t) is obtained by dividing the transform of f (t) by jω and adding the result to the impulse term that reflects the dc component F(0). • Note that the upper bound of the integral is t. • If it were not, the Fourier transform would be of a constant. 20

Reversal • In reversal: • This property states that reversing f (t) about the time axis reverses F(ω) about the frequency axis. • This can be considered a special case of time scaling if a=-1. 21

Duality and Convolution • Duality states • This expresses the symmetry property of the Fourier transform. • Convolution states: • An example of how this works is shown below: 22

Convolution • Here is a graphical representation of convolution: 23

Fourier Transform Pairs 24

More Fourier Transform Pairs 25

Circuit Applications • We can apply Fourier transforms to circuits with non -sinusoidal excitations in exactly the same way we apply phasor techniques to circuits with sinusoidal excitations. • Thus, Ohm’s law is still valid: • We get the same expressions for impedances as in phasor analysis 26

27

Circuit Applications II • Once transformed to frequency domain and the transform of the excitations are taken, the analysis of the circuit can proceed as has been done previously. • Note, though, that Fourier transforms can’t handle initial conditions. • The transfer function again defined as. 28

Example 10: Find v 0(t) in the circuit shown below for vi(t)=2 e-3 tu(t) 29

Solution: 30

Fourier vs. Laplace • Let us compare the Fourier transform with the Laplace transform: 1. The Laplace transform is one-sided in that the integral is over 0<t< making it only useful for positive time functions, f (t), t>0 The Fourier transform is applicable to functions defined for all time. 31

Fourier vs. Laplace II 2. For a function that is nonzero for positive time only, the two transforms are related by: – – This equation also shows that the Fourier transform can be regarded as a special case of the Laplace transform with s= jω Recall that s= + jω Therefore, this equation shows that the Laplace transform is related to the entire s plane, whereas the Fourier transform is restricted to the jω axis. 32

Fourier vs. Laplace III 3. The Laplace transform is applicable to a wider range of functions than the Fourier transform. – For example, the function tu(t) has a Laplace transform but no Fourier transform. But Fourier transforms exist for signals that are not physically realizable and have no Laplace transforms. 4. The Laplace transform is better suited for the analysis of transient problems involving initial conditions, since it permits the inclusion of the initial conditions, whereas the Fourier transform does not. 33