EECE 396 1 Hybrid and Embedded Systems Computation

EECE 396 -1 Hybrid and Embedded Systems: Computation T. John Koo, Ph. D. Institute for Software Integrated Systems Department of Electrical Engineering and Computer Science Vanderbilt University 300 Featheringill Hall February 5, 2004 john. koo@vanderbilt. edu http: //www. vuse. vanderbilt. edu/~kootj
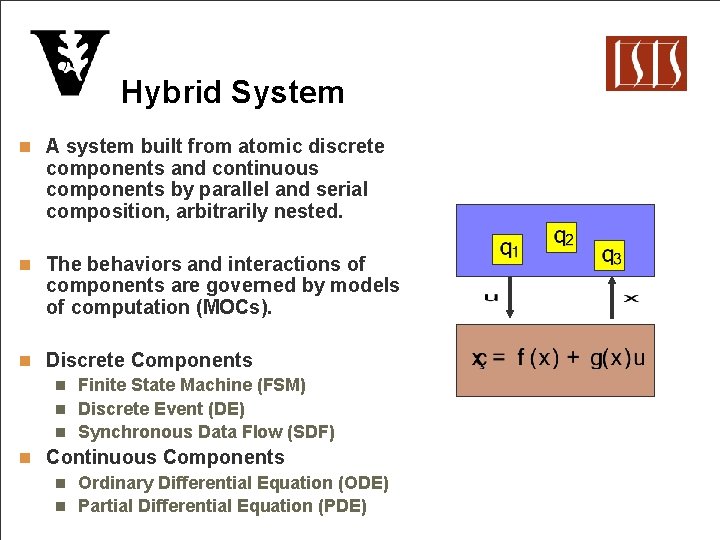
Hybrid System n A system built from atomic discrete components and continuous components by parallel and serial composition, arbitrarily nested. n The behaviors and interactions of components are governed by models of computation (MOCs). n Discrete Components n Finite State Machine (FSM) n Discrete Event (DE) n Synchronous Data Flow (SDF) n Continuous Components n Ordinary Differential Equation (ODE) n Partial Differential Equation (PDE)

Modeling: Hybrid Automata

Topics n Hybrid Automata Definitions n Examples n n Properties n n n Bouncing Ball Thermostat Executions Non-Determinism Blocking Zeno Executions Ref: n n n [1] J. Lygeros, Lecture Notes on Hybrid Systems, Cambridge, 2003. [2] J. Lygeros, C. Tomlin, and S. Sastry, The Art of Hybrid Systems, July 2001. [3] Thomas A. Henzinger , The theory of hybrid automata, Proceedings of the 11 th Annual IEEE Symposium on Logic in Computer Science, pp. 278 -292, 1996.

Why Hybrid Systems? n Modeling abstraction of Continuous systems with phased operation (e. g. walking robots, mechanical systems with collisions, circuits with diodes) n Continuous systems controlled by discrete inputs (e. g. switches, valves, digital computers) n Coordinating processes (multi-agent systems) n n Important in applications Hardware verification/CAD, real time software n Manufacturing, communication networks, multimedia n n Large scale, multi-agent systems Automated Highway Systems (AHS) n Air Traffic Management Systems (ATM) n Uninhabited Aerial Vehicles (UAV) n Power Networks n
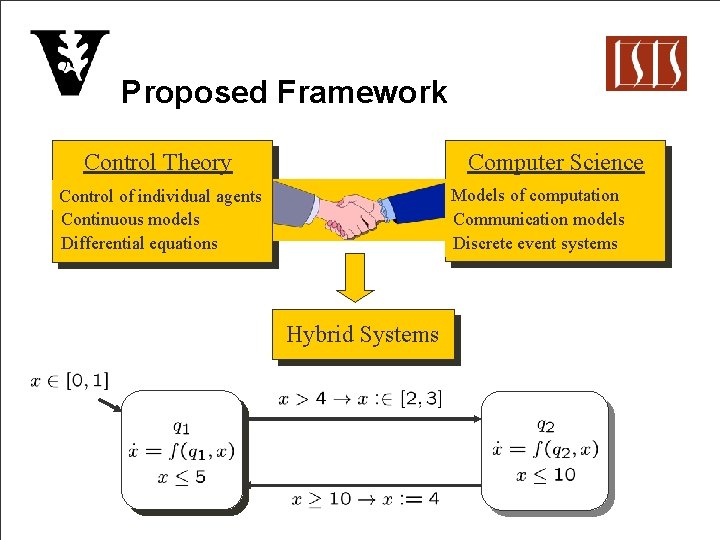
Proposed Framework Control Theory Computer Science Models of computation Communication models Discrete event systems Control of individual agents Continuous models Differential equations Hybrid Systems

Hybrid Automaton n Hybrid Automaton (Lygeros, 2003)
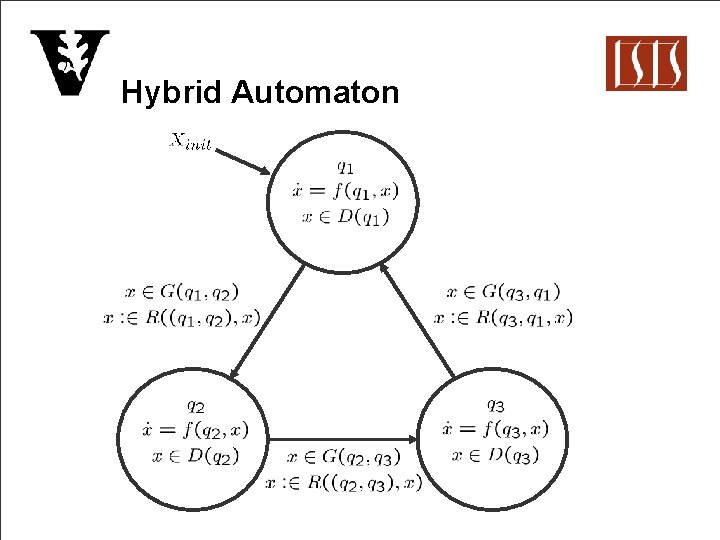
Hybrid Automaton
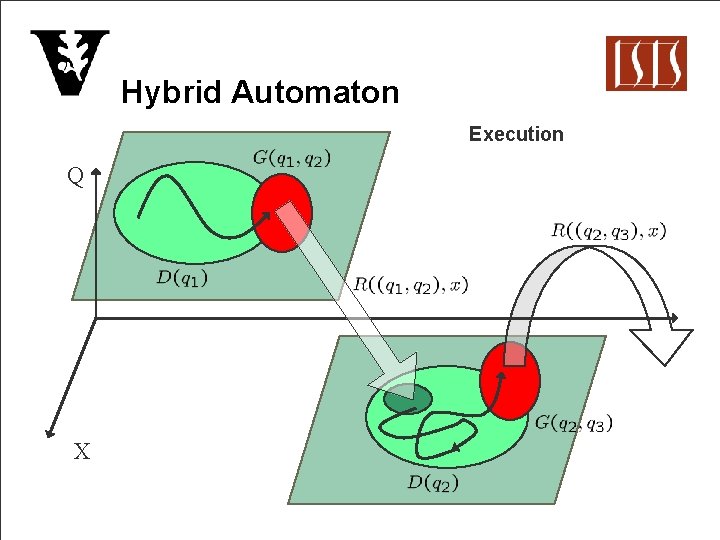
Hybrid Automaton Execution Q X
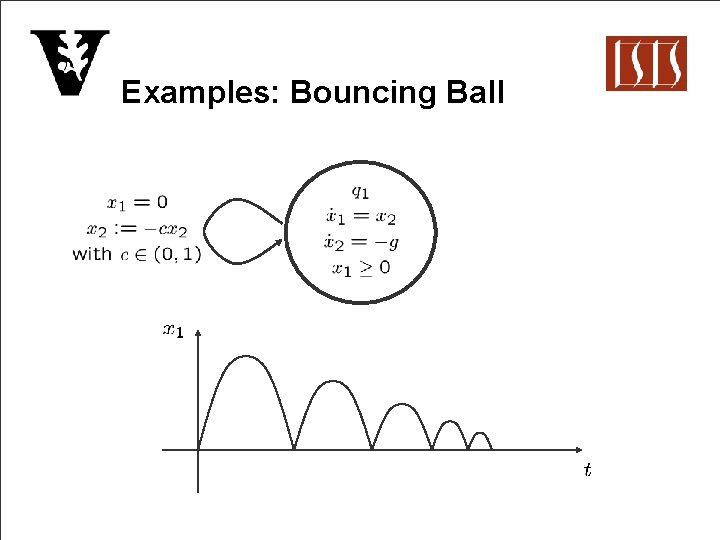
Examples: Bouncing Ball
Hy. Visual http: //ptolemy. eecs. berkeley. edu/ptolemy. II/hyvisual 2. 2/

Examples: Bouncing Ball

Examples: Bouncing Ball
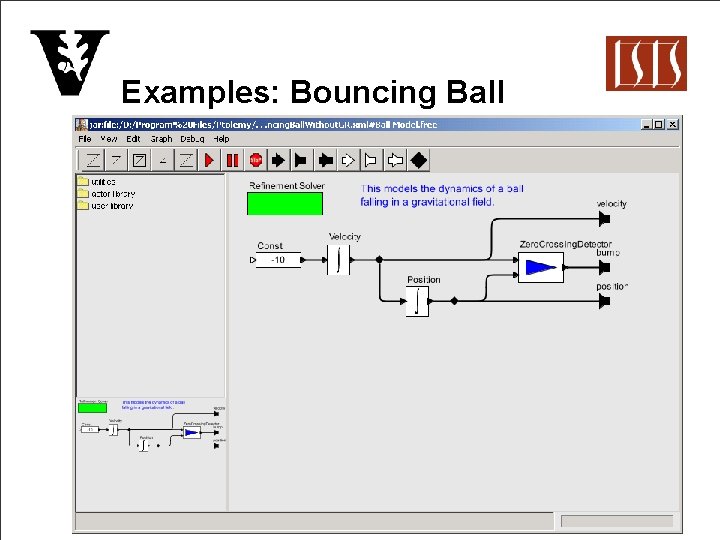
Examples: Bouncing Ball
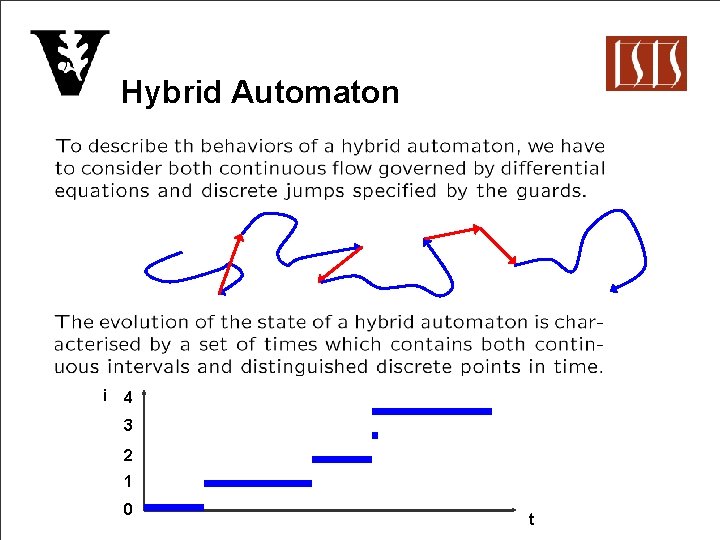
Hybrid Automaton i 4 3 2 1 0 t

Hybrid Automaton i 4 3 2 1 0 t

Hybrid Automaton i 4 3 2 1 0 t

Hybrid Automaton

Hybrid Automaton i i 2 2 1 1 0 0 finite t infinite t

Hybrid Automaton i i 2 2 1 1 0 0 finite t Zeno t

Hybrid Automaton n Zeno of Elea, 490 BC n Ancient Greek philosopher n The race of Achilles and the turtle n Achilles, a renowned runner, was challenged by the turtle to a race. Being a fair sportsman, Achilles decided to give the turtle a 10 meter head-start. To overtake the turtle, Achilles will have to first cover half the distance separating them. To cover the remaining distance, he will have to cover half that distance, and so on. n No matter how fast Achilles is, he can never overtake the turtle. Why? ? ? Ans: Covering each one of the segments in this series requires a non zero amount of time. Since there is an infinite number of segments, Achilles will never overtake the turtle. n

Hybrid Automaton n Non-Determinism n Multiple Executions for the same initial condition n Sources of non-determinism n n Non-Lipschitz continuous vectorfields, f Multiple discrete transition destinations, E & G Choice between discrete transition and continuous evolution, D & G Non-unique continuous state assignment, R Definition: A hybrid automaton H is deterministic if for all initial conditions there exists a unique maximal sequence
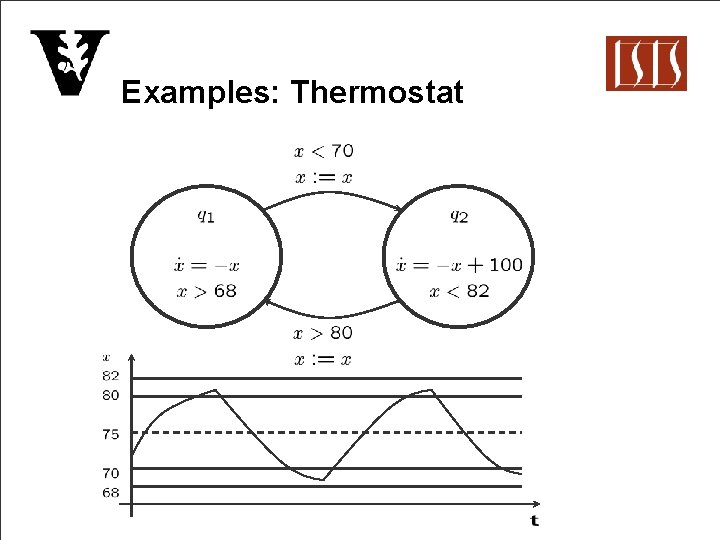
Examples: Thermostat

Hybrid Automaton n Blocking n No Infinite executions for some initial states n Source of blocking n n Cannot continue in domain due to reaching the boundary of the domain where no guard is defined Have no place to make discrete transition to Definition: A hybrid automaton H is non-blocking if for every initial condition there exists at least one infinite execution ?

Hybrid Automaton n Zeno Executions n Infinite execution defined over finite time n n Infinite number of transitions in finite time Transition times converge Definition: A hybrid automaton H is zeno if there exists an initial condition for which all infinite executions are Zeno
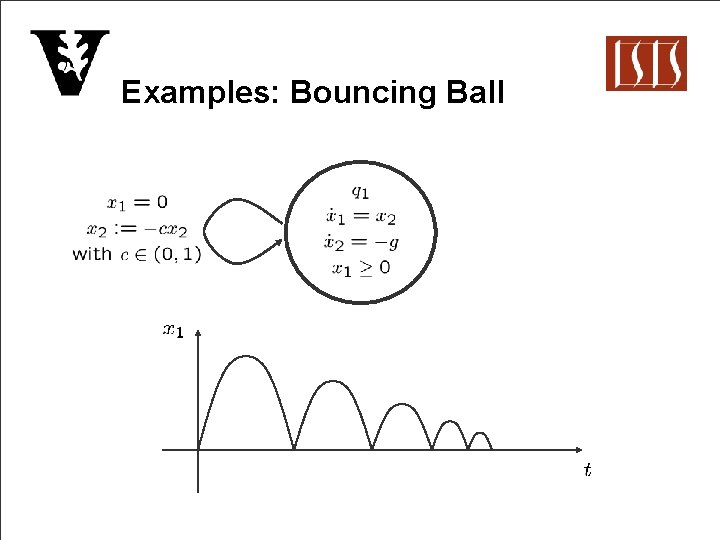
Examples: Bouncing Ball

End
- Slides: 27


















































