EE 599 020 Audio Signals and Systems Psychoacoustics
















- Slides: 23

EE 599 -020 Audio Signals and Systems Psychoacoustics (Pitch) Kevin D. Donohue Electrical and Computer Engineering University of Kentucky

Pitch is that attribute of auditory sensation in terms of which sounds may be ordered on a scale extending from low to high. Pitch depends mainly on the frequency content of the sound stimulus but it also depends on the sound pressure and the waveform of the stimulus. --- American National Standards (ANSI) 1994

Operational Definition A sound is said to have a certain pitch if it can be reliably matched by adjusting the frequency of a sine tone with arbitrary amplitude. --- William M. Hartmann, Signals, Sound, and Sensation, Springer-Verlag New York, Inc, 1998

Pitch Shifts Sound intensity affects pitch. Stephens rule was quantified in an experiment by Terhardt el. al. (1982) to show the relative pitch shift of a tone at F in k. Hz and L in d. B SPL is given by: Pitch shifts are also observed for changes in signal envelope shape, prior excitation, and noise in other bands.

Pitch and Frequency Most experiments indicate a. 5% frequency shift for the DL, which translates to 9 cents (or 9/100 of a semitone). A complex signal (multiple tones) can result in a pitch that is not close to any tones in the stimulus signal. This is common for harmonic tones with a missing fundamental.

Pitch Scale Units For simple tones, pitch and frequency are related, but not in a one to one manner. Experiments by Stevens and Volkman (1940) had subjects adjusted tones to create equal pitch intervals. From these results a psychoacoustic scale described in units of mels was created. Ø 1000 mels is equivalent to a 1000 Hz tone at 40 Phons. Ø 0 mels is equal to 20 Hz tone, and 20 k. Hz tone is about equal to 3500 mels. Ø From 1000 mels to 2000 mels represents a doubling of pitch and corresponds to a tripling on a frequency scale in Hz (1000 to 3000 Hz) Ø There appears to be good agreement with the mel scale and distance along the basilar membrane. Ø A critical band values range approximately from 100 to 180 mels, and mappings of frequency in Hz to barks has a similar shape as the mapping from frequency in Hz to pitch in mels. Ø However, the psychoacoustic mel scale is at odds with the music scale with is based more integer multiples of the frequency scale.

Complex Tones Ø For complex tones based on harmonic combinations of simple tones (single frequencies) the pitch is the frequency matched to the fundamental (even if it is missing). Ø For the rest of the notes, the pitch of a complex tone will be taken as the operational definition of pitch, which is more consistent with musical perception of pitch.

Fourier Series Recall that any realistic (finite power) periodic signal, s(t), can be expressed as a sum of weighted sinusoids, where the frequencies of the sinusoids are harmonically related to the fundamental frequency (period) of s(t): where f 0 is consider the fundamental frequency and all components nf 0 for n>1 are considered the harmonics or partials. The coefficients An relate to the power content of the signal at each harmonic (A 0 is the DC content of the signal).

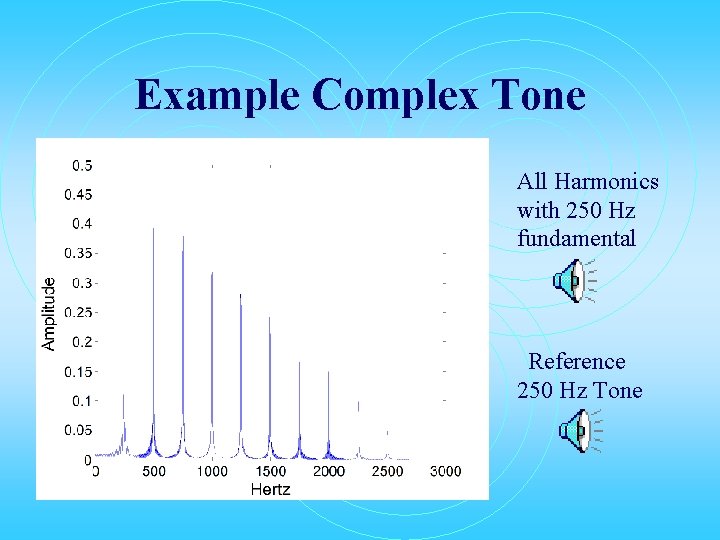
Example Complex Tone All Harmonics with 250 Hz fundamental Reference 250 Hz Tone

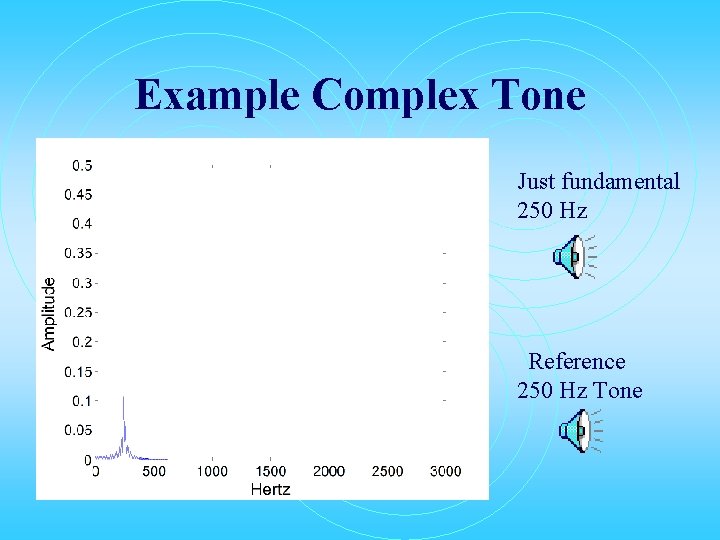
Example Complex Tone Just fundamental 250 Hz Reference 250 Hz Tone

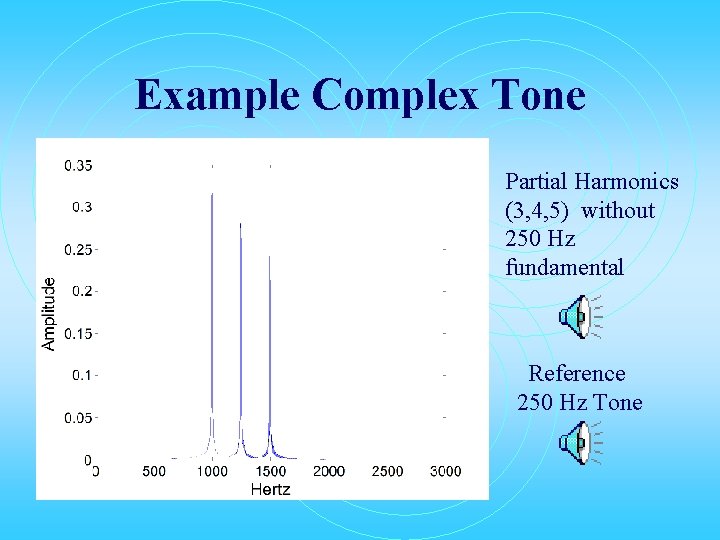
Example Complex Tone Partial Harmonics (3, 4, 5) without 250 Hz fundamental Reference 250 Hz Tone

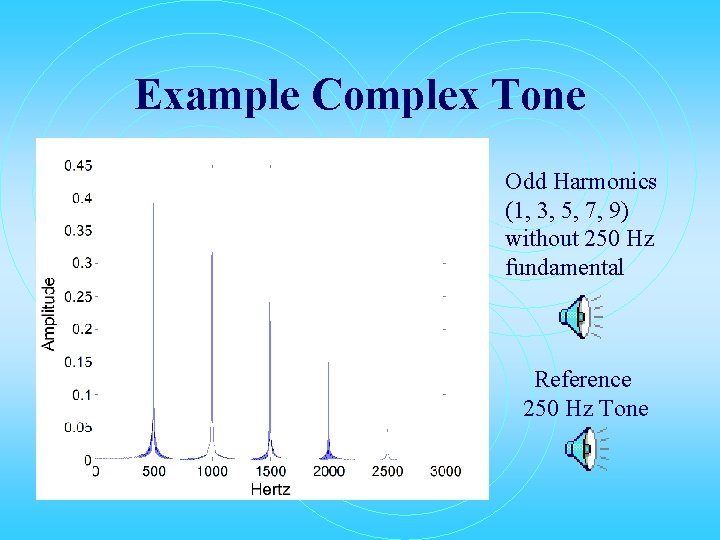
Example Complex Tone Odd Harmonics (1, 3, 5, 7, 9) without 250 Hz fundamental Reference 250 Hz Tone

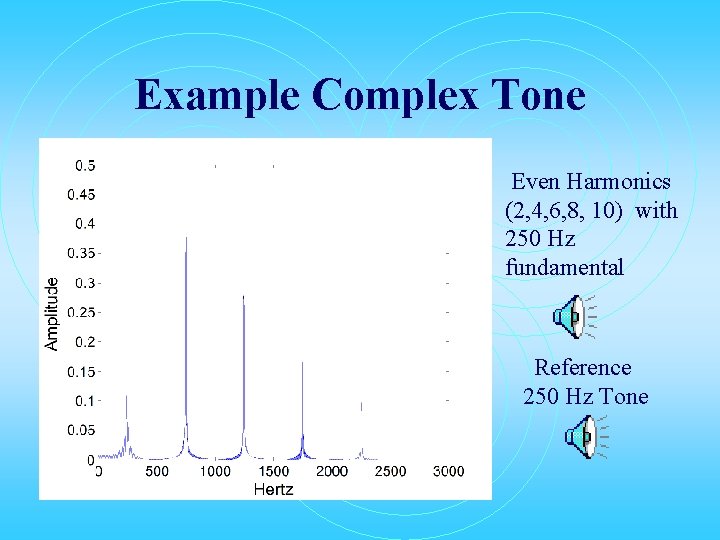
Example Complex Tone Even Harmonics (2, 4, 6, 8, 10) with 250 Hz fundamental Reference 250 Hz Tone

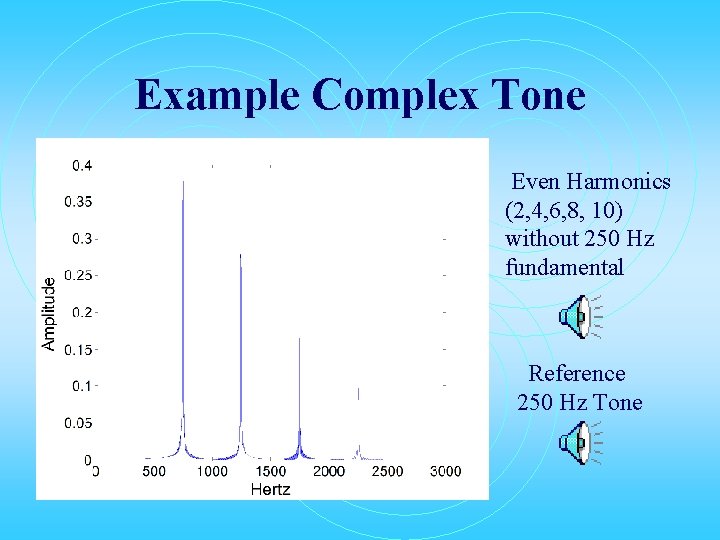
Example Complex Tone Even Harmonics (2, 4, 6, 8, 10) without 250 Hz fundamental Reference 250 Hz Tone

Example Complex Tone All Harmonics (2, 4… 10) without 250 Hz fundamental Reference 250 Hz Tone

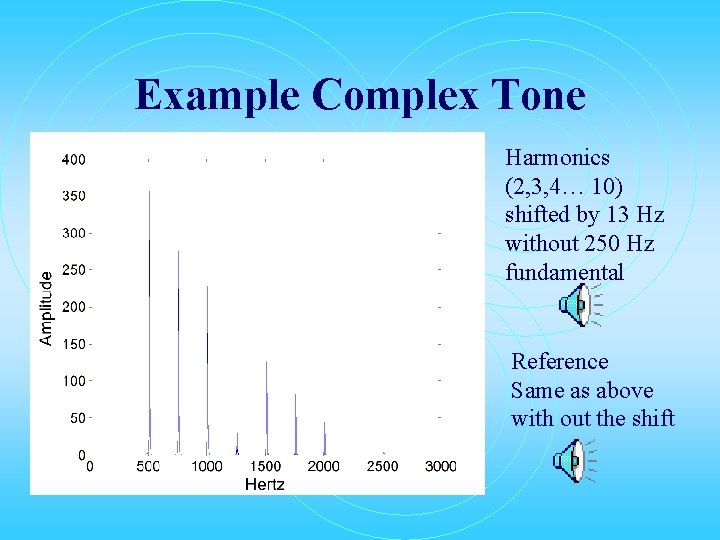
Example Complex Tone Harmonics (2, 3, 4… 10) shifted by 13 Hz without 250 Hz fundamental Reference Same as above with out the shift

Complex Tone Script % This script generates a series of complex tones to examine % the signal characteristics that determine pitch. This % script requires the program TONEC to run. % Written by Kevin D. Donohue 2/2004 fs = 11025; % Set Sampling Frequency f 0 = 250; % Set fundamental frequency % Set duration to at least 5 periods or 2 seconds, whichever is greater. int = max([2, round(fs*5/f 0)]); % Tone vector describing partial frequencies and relative amplitudes f = [f 0 1; 2*f 0. 9; 3*f 0. 8; 4*f 0. 7; . . . 5*f 0. 6; 6*f 0. 5; 7*f 0. 4; 8*f 0. 3; . . . 9*f 0. 2; 10*f 0. 1]; % Generate tone signals allhar = tonec(f, int, fs); % Tone will all harmonics wavwrite(allhar/(max(abs(allhar))+eps), fs, 'allhar. wav ') fund = tonec(f(1, : ), int, fs); % Tone with just fundamental wavwrite(fund/(max(abs(fund))+eps), fs, 'fund. wav') parthar = tonec(f(4: 6, : ), int, fs); % Tone with harmonics 4 -6 wavwrite(parthar/(max(abs(parthar))+eps), fs, 'parthar. wav ') oskiphar = tonec(f(2: 2: end, : ), int, fs); % Tone with odd harmonics wavwrite(oskiphar/(max(abs(oskiphar))+eps), fs, 'oskiphar. wav') eskiphar = tonec(f(1: 2: end, : ), int, fs); % Tone with even harmonics wavwrite(eskiphar/(max(abs(eskiphar))+eps), fs, 'eskiphar. wav ') epartskiphar = tonec(f(3: 2: end, : ), int, fs); % Tone with even harmonics minus fundamental wavwrite(epartskiphar/(max(abs(epartskiphar))+eps), fs, 'epartskiphar. wav' ) emfundhar = tonec(f(2: end, : ), int, fs); % Tone with all harmonics minus fundamental wavwrite(emfundhar/(max(abs(emfundhar))+eps), fs, 'emfundhar. wav ') sht = 13; % Frequency shift in Hz to examine effects of non harmonic shifts % Create matrix for shifted frequency harmonics fsht = f; fsht(: , 1) = f(: , 1)+sht; emfundhars = tonec(fsht(2: end, : ), int, fs); % Tone with all shifted harmonics minus fundamental wavwrite(emfundhars/(max(abs(emfundhars))+eps), fs, 'emfundhars. wav' )

Complex Tone Script % Spectral analysis of signals % Select Frequency window in terms of samples % it should include at least 5 periods and be % no bigger than 4096 samples. fwin = min([round(fs*5/f 0), 4096]); fax = fs*[0: fwin-1]/(2*fwin); % Create Frequency Axis % Compute FFT, zero padd to twice length for interpolated points pd = fft(allhar(1: fwin), 2*fwin); % Plot spectrum squared and normalize by time interval to get power figure(1); plot(fax, (abs(pd(1: fwin)). ^2)/fwin) set(1, 'Position', [232 269 512 409]) ca = get(1, 'Current. Axes'); % Plot only the first 3 k. Hz for better viewing of detail, you % may need to change this if your harmonics exceed 3000 Hz set(ca, 'XLim', [0 3000], 'Font. Size', 12) xlabel('Hertz', 'Font. Size', 14) ylabel('Amplitude', 'Font. Size', 14) % Do the same for all the other signal vectors

Example Discussion Ø What characteristics of a harmonic signal influences pitch? Ø How can an implied fundamental or pitch be determined from partial harmonics? (i. e. Knowing the harmonic content of the signal what process/algorithm would you use to find the pitch? )

Pitch Perception Theories Place theory – Hemholtz, pitch is determined by the stimulated place on the basilar membrane (recall tuning). Periodicity (timing) theory – Schouten, pitch is determined by the periodicity of the neural firings (recall synchrony).

Pitch Perception Theories Place theory – By masking the region of the basilar membrane where the fundamental of a harmonic sound should occur Licklider showed that place did not determine pitch. Periodicity (timing) theory – Schouten thought that the periodic excitation of the auditory nerves determined pitch and therefore were better resolved by the higher frequencies. Ritsma’s experiment showed the opposite (people preferred using lower frequencies to resolve pitch).

Homework (1) Create a sampled complex tone in a vector with at least 5 harmonics and at least 5 periods of the signal in a vector. Apply the FFT command in Matlab to plot the spectrum of this tone and plot the magnitude of its spectrum between 0 and FS/2 Hz (where FS is the sampling frequency). Explain how you would determine pitch from this graphic.

Homework (2) a) b) c) d) e) Determine the pitch that is likely to be perceived from these harmonic combinations: [220, 320, 420, 520] Hz [150 600 1050] Hz [200 600 800] Hz [100 200 600 800] Hz [300 305 310] Hz
 Psychoacoustics facts and models
Psychoacoustics facts and models Magni 575
Magni 575 The dewey decimal classification system was invented in?
The dewey decimal classification system was invented in? Tentukan taksiran ke ratusan terdekat dari 599 + 222
Tentukan taksiran ke ratusan terdekat dari 599 + 222 Cpsc 599
Cpsc 599 Animals and human language chapter 2
Animals and human language chapter 2 Arbitrariness in human language and animal language
Arbitrariness in human language and animal language Communicative signals and informative signals
Communicative signals and informative signals Chapter 6 audio basics
Chapter 6 audio basics Ktkp-020
Ktkp-020 Miller planes examples
Miller planes examples Nie cgcre 009
Nie cgcre 009 Series de fourier
Series de fourier Signals and systems oppenheim solutions chapter 5
Signals and systems oppenheim solutions chapter 5 Chen
Chen Precedence rule in signals and systems
Precedence rule in signals and systems Convolution sum in signals and systems
Convolution sum in signals and systems Pulse train fourier transform
Pulse train fourier transform Convolution integral
Convolution integral Introduction to signals and systems
Introduction to signals and systems Convolution sum in signals and systems
Convolution sum in signals and systems Signals and systems
Signals and systems Signal and systems
Signal and systems Elementary signal
Elementary signal













































