EE 3321 ELECTROMAGENTIC FIELD THEORY Week 2 Vector





























- Slides: 31

EE 3321 ELECTROMAGENTIC FIELD THEORY Week 2 Vector Operators Divergence and Stoke’s Theorems

Gradient Operator �The gradient is a vector operator denoted � and sometimes also called “del. ” It is most often applied to a real function of three variables. �In Cartesian coordinates, the gradient of f(x, y, z) is given by grad (f) = � f = x ∂f/∂x + y ∂f/∂ + z ∂f/∂z �The expression for the gradient in cylindrical and spherical coordinates can be found on the inside back cover of your textbook.

Significance of Gradient �The direction of grad(f) is the orientation in which the directional derivative has the largest value and |grad(f)| is the value of that directional derivative. �Furthermore, if grad(f) ≠ 0, then the gradient is perpendicular to the “level” curve z = f(x, y)

Example �As an example consider the gravitational potential on the surface of the Earth: V(z) = -gz where z is the height � The gradient of V would be �V = z ∂V/∂z = -g az

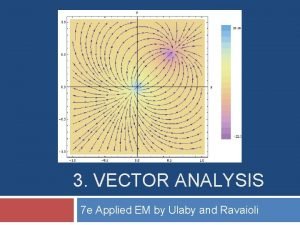
Exercise �Consider the gradient represented by the field of blue arrows. Draw level curves normal to the field.

Exercise �Calculate the gradient of �f = x 2 + y 2 �f = 2 xy �f = ex sin y

Exercise �Consider the surface z 2 = 4(x 2 + y 2). Find a unit vector that is normal to the surface at P: (1, 0, 2).

Laplacian Operator �The Laplacian of a scalar function f(x, y , z) is a scalar differential operator defined by 2 f = [∂ 2 /∂x 2 + ∂ 2 /∂y 2 + ∂ 2 /∂z 2 ]f �� � The expression for the Laplacian operator in cylindrical and spherical coordinates can be found in the back cover of your textbook. �The Laplacian of a vector A is a vector.

Applications �The Laplacian quite important in electromagnetic field theory: �It appears in Laplace's equation 2 f = 0 � �the Helmholtz differential equation 2 f + k 2 f = 0 � �and the wave equation 2 f = (1/c)2 ∂2 f/∂x 2 �

Exercise �Calculate the Laplacian of: �f = sin 0. 1πx �f = xyz �f = cos( kxx ) cos( kyy ) sin( kzz )

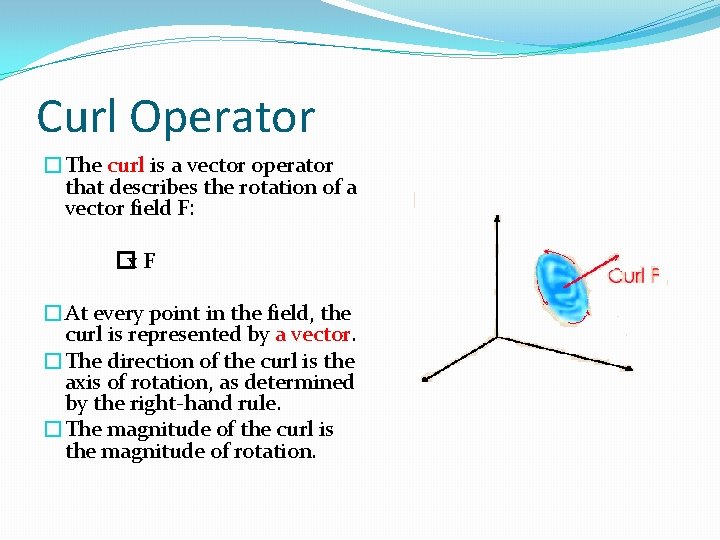
Curl Operator �The curl is a vector operator that describes the rotation of a vector field F: �x F �At every point in the field, the curl is represented by a vector. �The direction of the curl is the axis of rotation, as determined by the right-hand rule. �The magnitude of the curl is the magnitude of rotation.

Definition of Curl where the right side is a line integral around an infinitesimal region of area A that is allowed to shrink to zero via a limiting process and n is the unit normal vector to this region.

Line Integral �A line integral is an integral where the function is evaluated along a predetermined curve.

Significance of Curl �The physical significance of the curl of a vector field is the amount of "rotation" or angular momentum of the contents of given region of space.

Exercise �Consider the field shown here. �If we stick a paddle wheel in the first quadrant would it rotate? �If so, in which direction?

Curl in Cartesian Coordinates �In practice, the curl is computed as �The expression for the curl in cylindrical and spherical coordinates can be found on the inside back cover of your textbook.

Exercise �Find the curl of F = x ax + yz ay – (x 2 + z 2) az.

Divergence Operator �The divergence is a vector operator that describes the extent to which there is more “flux” exiting an infinitesimal region of space than entering it: �· F �At every point in the field, the divergence is represented by a scalar.

Definition of Divergence where the surface integral is over a closed infinitesimal boundary surface A surrounding a volume element V, which is taken to size zero using a limiting process.

Surface Integral �It’s the integral of a function f(x, y, z) taken over a surface.

Example �Consider a field F = Fo/r 2 ar. Show that the ratio of the flux coming out of a spherical surface of radius r=a to the volume of the same sphere is = 3 F o/4 a 3 �First calculate �Then calculate = 4 π Fo V = 4π a 3/3

Significance of Divergence �The divergence of a field is the extent to which the vector field flow behaves like a source at a given point.

Divergence in Cartesian Coordinates �In practice the divergence is computed as �The expression for the divergence in cylindrical and spherical coordinates can be found on the inside back cover of your textbook.

Exercise �Determine the following: �divergence of F = 2 x ax + 2 y ay. �divergence of the curl of F = 2 x ax + 2 y ay.

Divergence Theorem �The volume integral of the divergence of F is equal to the flux coming out of the surface A enclosing the selected volume V : �The divergence theorem transforms the volume integral of the divergence into a surface integral of the net outward flux through a closed surface surrounding the volume.

Example �Consider the “finite volume” electric charge shown here. �The divergence theorem can be used to calculate the net flux outward and the amount of charge in the volume. �Requirement: the field must be continuous in the volume enclosed by the surface considered.

Exercise �Consider a spherical surface of radius r = b and a field F = (r/3) ar. �Show that the divergence of F is 1. �Show that the volume integral of the divergence is (4π/3) b 3 �Show that the flux of F coming out of the spherical surface is (4π/3) b 3

Stokes' Theorem �It states that the area integral of the curl of F over a surface A is equal to the closed line integral of F over the path C that encloses A: �Stoke’s Theorem transforms the circulation of the field into a line integral of the field over the contour that bounds the surface.

Significance of Stoke’s Theorem �The integral is a sum of circulation differentials. �The circulation differential is defined as the dot product of the curl and the surface area differential over which it is measured.

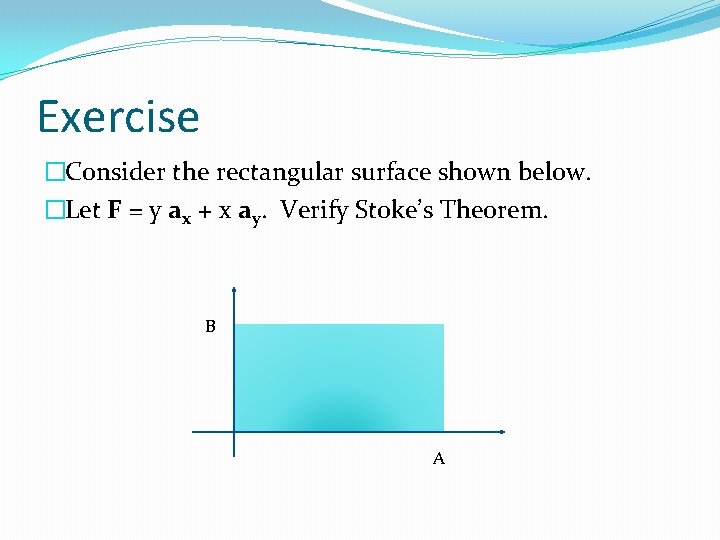
Exercise �Consider the rectangular surface shown below. �Let F = y ax + x ay. Verify Stoke’s Theorem. B A

Homework �Read book sections 3 -3, 3 -4, 3 -5, 3 -6, and 3 -7. �Solve end-of-chapter problems � 3. 32, 3. 35, 3. 49, 3. 39, 3. 41, 3. 43, 3. 45, 3. 48
 Electromagnetic waves scale
Electromagnetic waves scale Week by week plans for documenting children's development
Week by week plans for documenting children's development Directed line segment vs vector
Directed line segment vs vector Coordenadas cartesianas
Coordenadas cartesianas Why is vector resolution the opposite of vector addition
Why is vector resolution the opposite of vector addition What is the definition of position vector
What is the definition of position vector Curl formula in spherical coordinates
Curl formula in spherical coordinates Vector field histogram
Vector field histogram Flux of a vector field
Flux of a vector field Divergence and curl of a vector field
Divergence and curl of a vector field Surface integral
Surface integral Is time a vector or scalar
Is time a vector or scalar Electric feild equations
Electric feild equations Vector field sketcher
Vector field sketcher Curl of the vector field
Curl of the vector field Green's theorem formula
Green's theorem formula Vector field
Vector field Electric field and magnetic field difference
Electric field and magnetic field difference Field dependent vs field independent
Field dependent vs field independent Field dependent vs field independent
Field dependent vs field independent Q factor of capacitor
Q factor of capacitor Waveguide cutoff frequency
Waveguide cutoff frequency Data types and field properties
Data types and field properties Field dependent and field independent
Field dependent and field independent Magnetic field
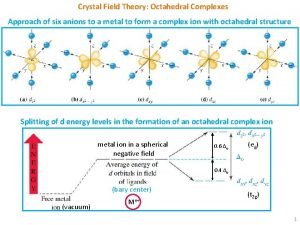
Magnetic field Teori medan kristal
Teori medan kristal Forces for change
Forces for change Gestalt psychology
Gestalt psychology Gestalt psychology
Gestalt psychology Site:slidetodoc.com
Site:slidetodoc.com Trigonal bipyramidal crystal field splitting diagram
Trigonal bipyramidal crystal field splitting diagram Salient features of cft
Salient features of cft