DYNAMICS KINEMATICS OF A PARTICLES CO 4 Ability

DYNAMICS : KINEMATICS OF A PARTICLES CO 4: Ability to solve problems which relate to kinematics and kinetics of a particle WAN AMIZA AMNEERA WAN AHMAD SCHOOL ENVIRONMENTAL ENGINEERING

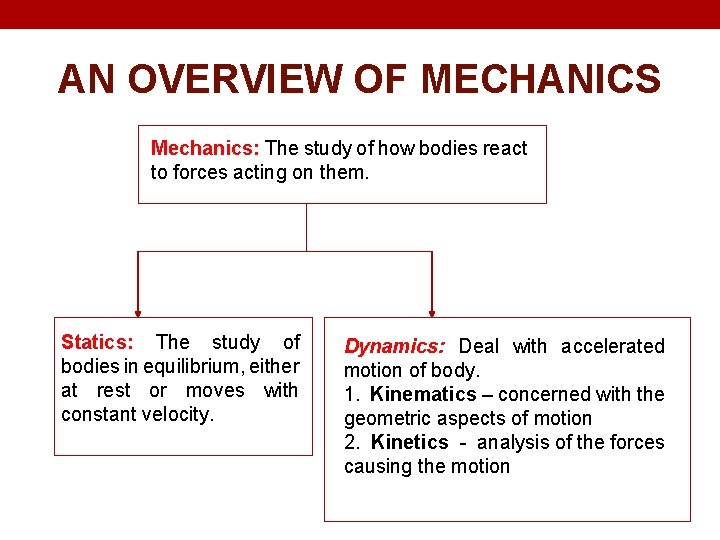
AN OVERVIEW OF MECHANICS Mechanics: The study of how bodies react to forces acting on them. Statics: The study of bodies in equilibrium, either at rest or moves with constant velocity. Dynamics: Deal with accelerated motion of body. 1. Kinematics – concerned with the geometric aspects of motion 2. Kinetics - analysis of the forces causing the motion

1. 0 CONTINUOUS MOTION (STRAIGHT LINE MOTION)

1. 1 POSITION • A particle travels along a straight-line path defined by the coordinate axis s. • The position of the particle at any instant, relative to the origin, O, is defined by the position vector r, or the scalar s. Scalar s can be positive or negative. Typical units for r and s are meters (m) or feet (ft).

1. 2 DISPLACEMENT • The displacement of the particle is defined as its change in position. • The total distance traveled by the particle, s. T, is a positive scalar that represents the total length of the path over which the particle travels. Vector form: r = r’ - r Scalar form: s = s’ - s

1. 3 VELOCITY • Velocity is a measure of the rate of change in the position of a • • • particle. It is a vector quantity (it has both magnitude and direction). The magnitude of the velocity is called speed, with units of m/s or ft/s. The average velocity of a particle during a time interval t is vavg = r/ t The instantaneous velocity is the time-derivative of position. v = dr/dt Speed is the magnitude of velocity: v = ds/dt Average speed is the total distance traveled divided by elapsed time: (vsp)avg = s. T/ t Average velocity: vave = - Δs/Δt

1. 4 ACCELERATION • Acceleration is the rate of change in the velocity of a particle. It is a • • • vector quantity. Typical units are m/s 2 or ft/s 2. The instantaneous acceleration is the time derivative of velocity. Vector form: a = dv/dt Scalar form: a = dv/dt = d 2 s/dt 2 Acceleration can be positive (speed increasing) or negative (speed decreasing). A differential relation involving the displacement, velocity and acceleration along the path by eliminating the time differential, dt will gives: a ds = v dv

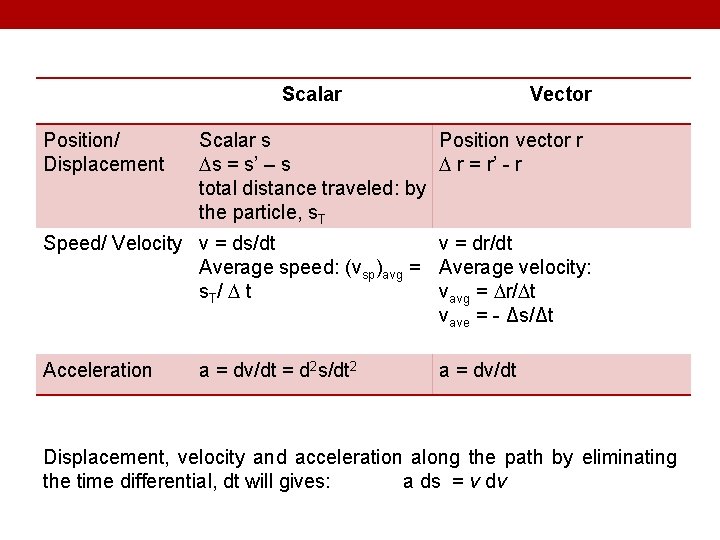
Scalar Position/ Displacement Vector Scalar s Position vector r s = s’ – s r = r’ - r total distance traveled: by the particle, s. T Speed/ Velocity v = ds/dt v = dr/dt Average speed: (vsp)avg = Average velocity: s. T/ t vavg = r/ t vave = - Δs/Δt Acceleration a = dv/dt = d 2 s/dt 2 a = dv/dt Displacement, velocity and acceleration along the path by eliminating the time differential, dt will gives: a ds = v dv

1. 5 CONSTANT ACCELERATION • The three kinematic equations can be integrated for the special case when acceleration is constant (a = ac) to obtain very useful equations. A common example of constant acceleration is gravity; i. e. , a body freely falling toward earth. In this case, ac = g = 9. 81 m/s 2 = 32. 2 ft/s 2 downward. These equations are: v t ò dv = ò a dt c vo o s t ò ds = ò v dt so v v = vo + act yields s = s o + v ot + (1/2)a ct 2 yields v 2 = (vo )2 + 2 ac(s - so) o s ò v dv = ò ac ds vo yields so

SUMMAR Y • Differentiate position to get velocity and acceleration. v = ds/dt ; a = dv/dt or a = v dv/ds • Integrate acceleration for velocity and position. Velocity: Position: v t v s vo o vo so ò dv = ò a dt or ò v dv = ò a ds s t so o ò ds = ò v dt • Note that so and vo represent the initial position and velocity of the particle at t = 0.

EXAMPLE 1. 1 • The car in figure moves in a straight line such that for a short time. Its velocity is defined by v = (0. 9 t 2 + 0. 6 t) m/s, where t is in seconds. Determine its position and acceleration when t = 3 s. When t = 0, s = 0.

2. 0 RECTILINEAR KINEMATICS: ERRATIC MOTION (erratic or discontinuity in motion)

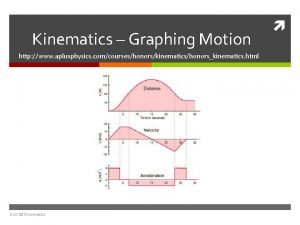
• When a particle’s motion during a time period is erratic / discontinuity in the motion, then it will be difficult to obtain a continuous mathematical function to describe its position, velocity or acceleration. • The motion may best be described graphically using a series of curves. • Graphing provides a good way to handle complex motions that would be difficult to describe with formulas. Graphs also provide a visual description of motion and reinforce the calculus concepts of differentiation and integration as used in dynamics.

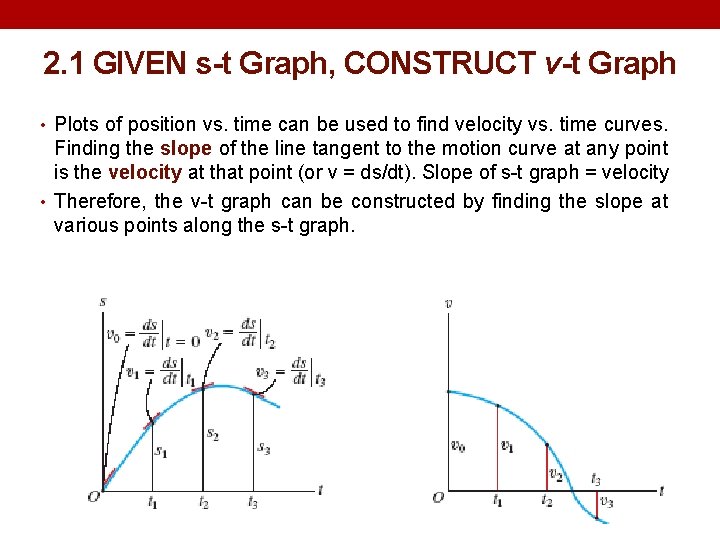
2. 1 GIVEN s-t Graph, CONSTRUCT v-t Graph • Plots of position vs. time can be used to find velocity vs. time curves. Finding the slope of the line tangent to the motion curve at any point is the velocity at that point (or v = ds/dt). Slope of s-t graph = velocity • Therefore, the v-t graph can be constructed by finding the slope at various points along the s-t graph.

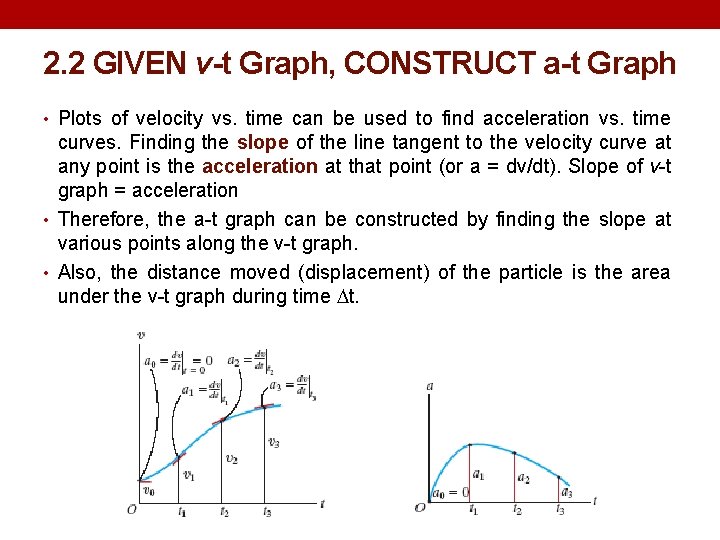
2. 2 GIVEN v-t Graph, CONSTRUCT a-t Graph • Plots of velocity vs. time can be used to find acceleration vs. time curves. Finding the slope of the line tangent to the velocity curve at any point is the acceleration at that point (or a = dv/dt). Slope of v-t graph = acceleration • Therefore, the a-t graph can be constructed by finding the slope at various points along the v-t graph. • Also, the distance moved (displacement) of the particle is the area under the v-t graph during time t.

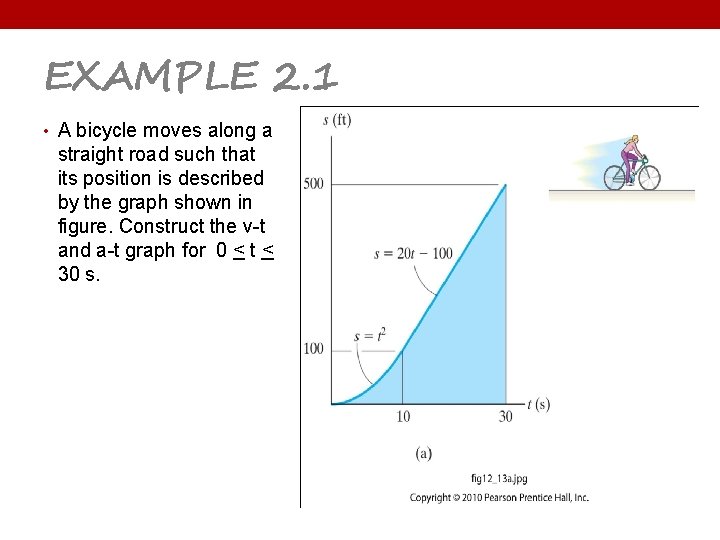
EXAMPLE 2. 1 • A bicycle moves along a straight road such that its position is described by the graph shown in figure. Construct the v-t and a-t graph for 0 < t < 30 s.

EXAMPLE 2. 2 If the position of the particle is defined as s = (5 t – 3 t 2) m, where t is in seconds, construct the s-t, v-t, and a-t graphs for 0 < t < 10 s.

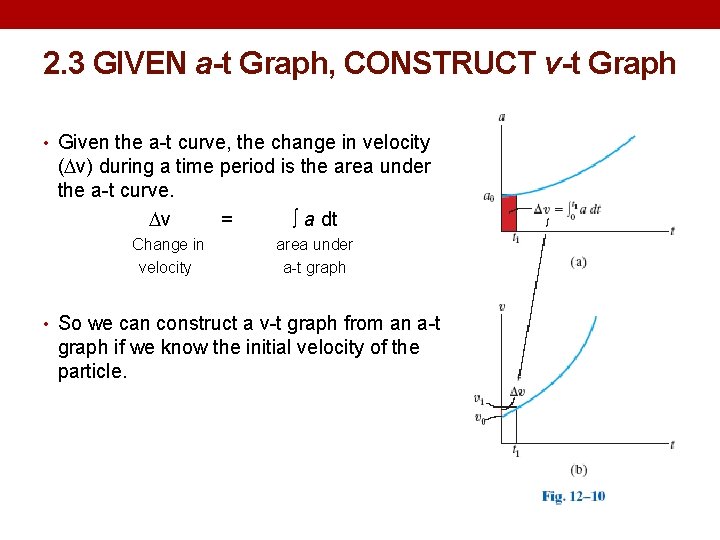
2. 3 GIVEN a-t Graph, CONSTRUCT v-t Graph • Given the a-t curve, the change in velocity ( v) during a time period is the area under the a-t curve. v = ∫ a dt Change in velocity area under a-t graph • So we can construct a v-t graph from an a-t graph if we know the initial velocity of the particle.

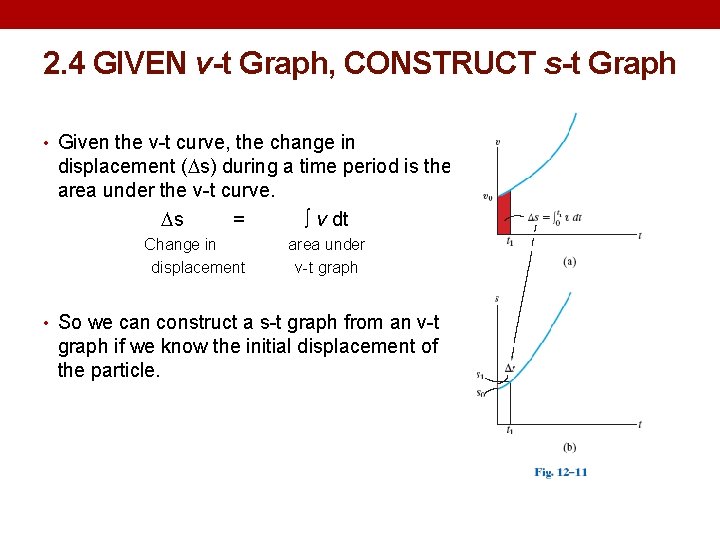
2. 4 GIVEN v-t Graph, CONSTRUCT s-t Graph • Given the v-t curve, the change in displacement ( s) during a time period is the area under the v-t curve. s = ∫ v dt Change in displacement area under v-t graph • So we can construct a s-t graph from an v-t graph if we know the initial displacement of the particle.

EXAMPLE 2. 3 • The test car in figure starts from the rest and travels along the straight track such that it accelerates 10 m/s 2 at a constant rate for 10 s and then decelerates 2 m/s 2 at a constant rate. Draw the v-t and s-t graphs and determine the time t’ needed to stop the car. How far has the car traveled?

EXAMPLE 2. 4 • The car travels along a straight road with the speed shown by the v-t graph. Determine the total distance the car travels until it stops when t = 48 s. Also plot the s-t and a-t graphs.

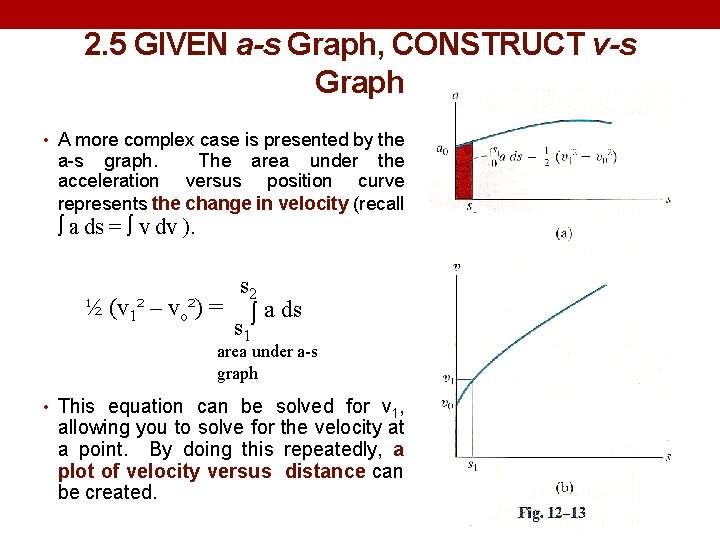
2. 5 GIVEN a-s Graph, CONSTRUCT v-s Graph • A more complex case is presented by the a-s graph. The area under the acceleration versus position curve represents the change in velocity (recall ò a ds = ò v dv ). s 2 ½ (v 1² – vo²) = ò a ds s 1 area under a-s graph • This equation can be solved for v 1, allowing you to solve for the velocity at a point. By doing this repeatedly, a plot of velocity versus distance can be created.

• Thus, the initial small segment of area under a-s graph, ∫a ds equal one-half the difference in the squares of the speed, ½(v 12 – v 02 ). • If the area is determined and the initial values of v 0 at s 0 = 0 is known, then v 1 = (2∫ a ds + vs 02) 1/2, figure 12 -13(b). 1 s 0 • Successive point on the v-s graph can be constructed in this manner starting from the initial velocity, v 0.

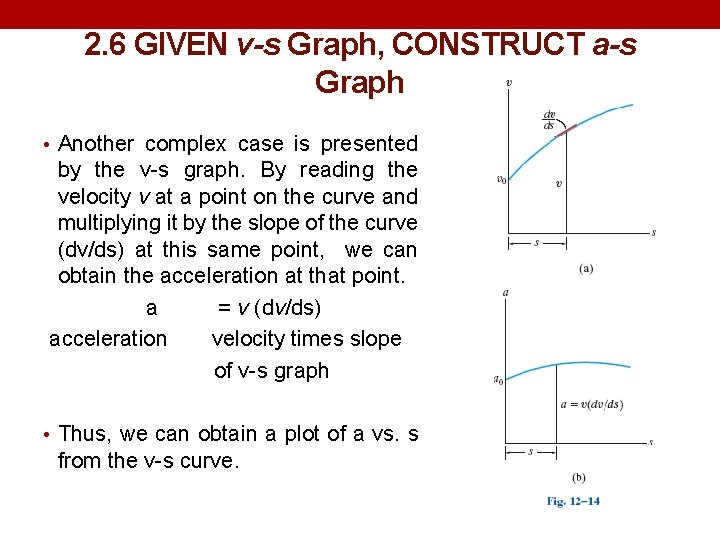
2. 6 GIVEN v-s Graph, CONSTRUCT a-s Graph • Another complex case is presented by the v-s graph. By reading the velocity v at a point on the curve and multiplying it by the slope of the curve (dv/ds) at this same point, we can obtain the acceleration at that point. a = v (dv/ds) acceleration velocity times slope of v-s graph • Thus, we can obtain a plot of a vs. s from the v-s curve.

EXAMPLE 2. 5 The v-s graph for a go-cart traveling on a straight road is shown. Determine the acceleration of the go-cart at s = 50 m and s = 150 m. Draw the a-s graph.

EXAMPLE 2. 6 The a-s graph for a train traveling along the straight track is given for the first 400 m of its motion. Plot the v-s graph. v = 0 at s = 0

3. 0 GENERAL CURVILINEAR MOTION

A particle moving along a curved path undergoes curvilinear motion. Since the motion is often three-dimensional, vectors are used to describe the motion. A particle moves along a curve defined by the path function, s. The position of the particle at any instant is designated by the vector r = r(t). Both the magnitude and direction of r may vary with time. If the particle moves a distance Δs along the curve during time interval Δt, the displacement is determined by vector subtraction: Δr = r’ - r

3. 1 VELOCITY • Velocity represents the rate of change in the position of a particle. • The average velocity of the particle during the time increment Δt is vavg = Δr/Δt. • The instantaneous velocity is the time- derivative of position v = dr/dt. • The velocity vector, v, is always tangent to the path of motion. • The magnitude of v is called the speed. Since the arc length Δs approaches the magnitude of Δr as t→ 0, the speed can be obtained by differentiating the path function (v = ds/dt). Note that this is not a vector!

3. 2 ACCELERATION • Acceleration represents the rate of change in the velocity of a particle. • If a particle’s velocity changes from v to v’ over a time increment Dt, the average acceleration during that increment is: aavg = Dv/Dt = (v - v’)/Dt • The instantaneous acceleration is the time- derivative of velocity: a = dv/dt = d 2 r/dt 2 • A plot of the locus of points defined by the arrowhead of the velocity vector is called a hodograph. The acceleration vector is tangent to the hodograph, but not, in general, tangent to the path function.

4. 0 CURVILINEAR MOTION: RECTANGULAR COMPONENTS

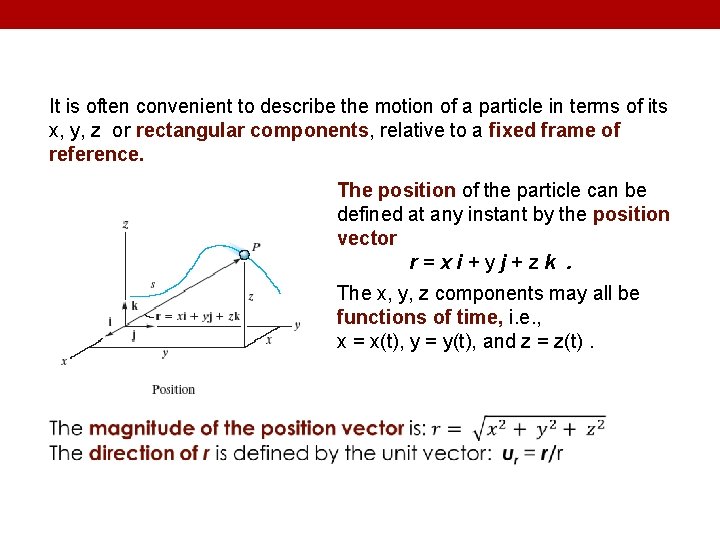
It is often convenient to describe the motion of a particle in terms of its x, y, z or rectangular components, relative to a fixed frame of reference. The position of the particle can be defined at any instant by the position vector r = x i + y j + z k. The x, y, z components may all be functions of time, i. e. , x = x(t), y = y(t), and z = z(t).

4. 1 VELOCITY The velocity vector is the time derivative of the position vector: v = dr/dt = d(xi)/dt + d(yj)/dt + d(zk)/dt Since the unit vectors i, j, k are constant in magnitude and direction, this equation reduces to v = vxi + vyj + vzk where vx = = dx/dt, v y = = dy/dt, v z = = dz/dt x • y • z •

4. 2 ACCELERATION The acceleration vector is the time derivative of the velocity vector (second derivative of the position vector): a = dv/dt = d 2 r/dt 2 = axi + ayj + azk • where ax = = = dv • • /dt, a = = = dv v • x v x y y x y • • y /dt, az = = = dv z /dt v • z z • • The direction of a is specified by the unit vector: u = a/a The direction usually not tangent to the path of the particle.

EXAMPLE 4. 1 A particle, originally at rest and located at point (3 m, 2 m, 5 m), is subjected to an acceleration of a = {6 ti + 12 t 2 k} m/s 2. Determine the particle’s position (x, y, z) at t = 1 s.

EXAMPLE 4. 2 The velocity of a particle is given by v = {16 t 2 i + 4 t 3 j + (5 t + 2 k)} m/s, where t is in seconds. If the particle is at the origin when t = 0, determine the magnitude of the particle’s acceleration when t = 2 s. Also, what is the x, y, z coordinate position at this instant?

5. 0 MOTION OF A PROJECTILE

Projectile motion can be treated as two rectilinear motions, one in the horizontal direction experiencing zero acceleration and the other in the vertical direction experiencing constant acceleration (i. e. , gravity). For illustration, consider the two balls on the left. The red ball falls from rest, whereas the yellow ball is given a horizontal velocity. Each picture in this sequence is taken after the same time interval. Notice both balls are subjected to the same downward acceleration since they remain at the same elevation at any instant. Also, note that the horizontal distance between successive photos of the yellow ball is constant since the velocity in the horizontal direction is constant.

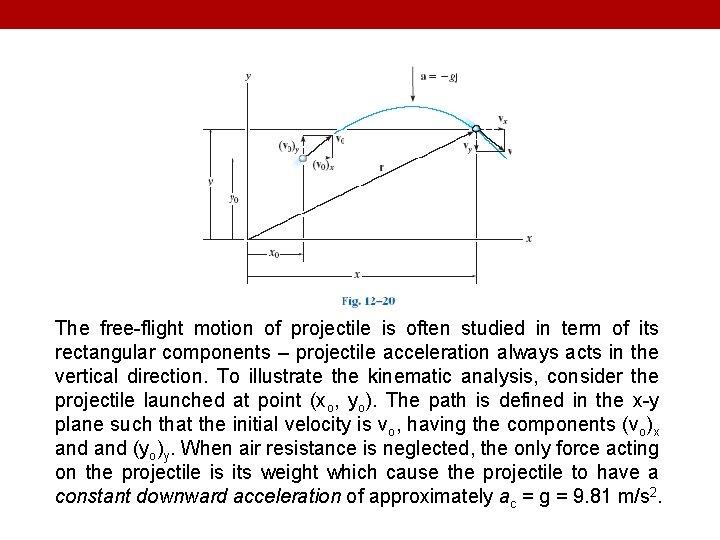
The free-flight motion of projectile is often studied in term of its rectangular components – projectile acceleration always acts in the vertical direction. To illustrate the kinematic analysis, consider the projectile launched at point (xo, yo). The path is defined in the x-y plane such that the initial velocity is vo, having the components (vo)x and (yo)y. When air resistance is neglected, the only force acting on the projectile is its weight which cause the projectile to have a constant downward acceleration of approximately ac = g = 9. 81 m/s 2.

5. 1 HORIZONTAL MOTION • Since ax = 0, application of the constant acceleration equations yields: (→) (→) v = v 0 + act ; vx = (v 0)x x = x 0 + v 0 t + ½ act 2 ; x = x 0 + (v 0)xt v 2 = v 02 + 2 ac(x – x 0) ; vx = (v 0)x The 1 st and last equation indicate that the horizontal component of velocity always remains constant during the motion.

5. 2 VERTICAL MOTION • Since the +ve y axis is directed upward, then ay = -g. Applying on constant acceleration equations, we get: (↑) (↑) v = v 0 + act ; vy = (v 0)y - gt y = y 0 + v 0 t + ½ act 2 ; y = y 0 + (v 0)yt - ½ gt 2 v 2 = v 02 + 2 ac(y – y 0) ; vy 2 = (v 0 )y 2 – 2 g(y – y 0) Last equation can be formulated on the basis of eliminating t between the 1 st two equation, therefore only two of the above equations are independent of one another.

EXAMPLE 5. 1 A sack slides off the ramp, with a horizontal velocity of 12 m/s. If the height of the ramp is 6 m, from the floor, determine the time needed for the sack to strike the floor and the range R where the sacks begin to pile up.

EXAMPLE 5. 2 The shipping machine is design to eject wood chips at v 0 = 7. 5 m/s as shown in figure. If the tube is oriented at 30° from the horizontal, determine how high h, the chips strike the pile if they land on the pile 6 m from the tube. 30 O

EXAMPLE 5. 3 The track for this racing event was designed so that riders jump off the slope at 30°, from a height of 1 m. During a race, it was observed that the rider shown in figure remained in mid air for 1. 5 s. Determine the speed at which he was traveling off the slope, the horizontal distance he travels before striking the ground, and the max height he attains. Neglect the size of bike and rider.

6. 0 ABSOLUTE DEPENDENT MOTION ANALYSIS OF TWO PARTICLES

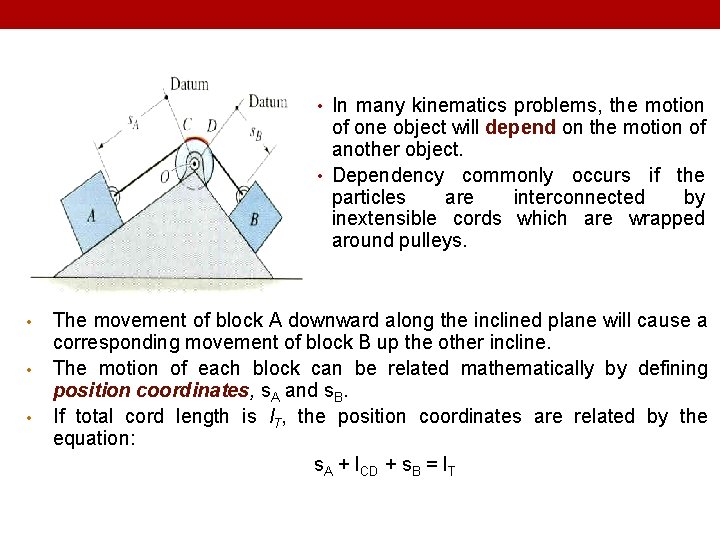
• In many kinematics problems, the motion of one object will depend on the motion of another object. • Dependency commonly occurs if the particles are interconnected by inextensible cords which are wrapped around pulleys. • • • The movement of block A downward along the inclined plane will cause a corresponding movement of block B up the other incline. The motion of each block can be related mathematically by defining position coordinates, s. A and s. B. If total cord length is l. T, the position coordinates are related by the equation: s. A + l. CD + s. B = l. T

• Here l. T is the total cord length and l. CD is the length of cord passing over arc CD on the pulley. • l. CD and l. T remain constant, while s. A and s. B measure the lengths of the changing segments of the cord. By taking the time derivation of this expression, we have: ds. A/dt + ds. B/dt = 0 or v. B = -v. A • The negative sign indicates that as A moves down the incline (positive s. A direction), B moves up the incline (negative s. B direction). • Accelerations can be found by differentiating the velocity expression: a. B = -a. A.

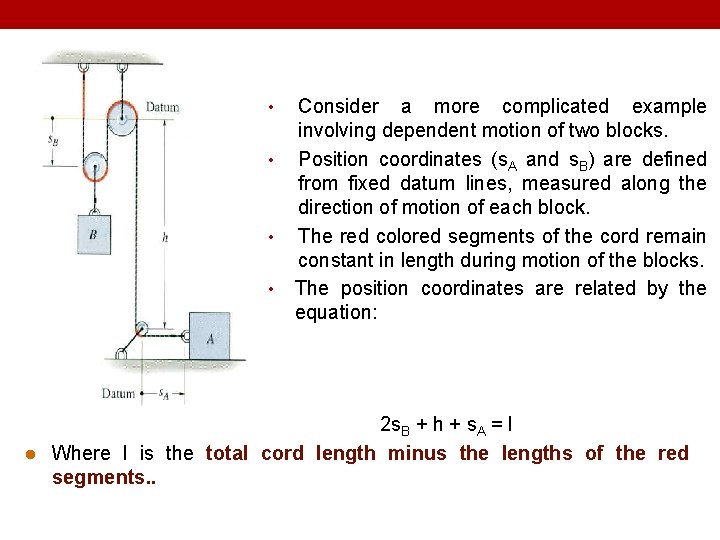
• • l Consider a more complicated example involving dependent motion of two blocks. Position coordinates (s. A and s. B) are defined from fixed datum lines, measured along the direction of motion of each block. The red colored segments of the cord remain constant in length during motion of the blocks. The position coordinates are related by the equation: 2 s. B + h + s. A = l Where l is the total cord length minus the lengths of the red segments. .

• • Since l and h remain constant during the motion, the velocities and accelerations can be related by two successive time derivatives: 2 v. B = -v. A and 2 a. B = -a. A When block B moves downward (+s. B), block A moves to the left (-s. A). s. B This example can also be worked by defining the position coordinate for B (s. B) from the bottom pulley instead of the top pulley. The position, velocity, and acceleration relations then become: 2(h – s. B) + h + s. A = l ; 2 v. B = v. A ; 2 a. B = a. A • The results are the same, but why the sign conventions are different than the previous formulation?

6. 1 DEPENDENT MOTION: PROCEDURES • These procedures can be used to relate the dependent motion of • • particles moving along rectilinear paths (only the magnitudes of velocity and acceleration change, not their line of direction). 1. Define position coordinates from fixed datum lines, along the path of each particle. Different datum lines can be used for each particle. 2. Relate the position coordinates to the cord length. Segments of cord that do not change in length during the motion may be left out. 3. If a system contains more than one cord, relate the position of a point on one cord to a point on another cord. Separate equations are written for each cord. 4. Differentiate the position coordinate equation(s) to relate velocities and accelerations. Keep track of signs!

EXAMPLE 6. 1 1. 2. 3. Determine the speed of block A in fig. 12. 38 if block B has an upward speed of 2 m/s. Determine the speed of block A in fig. 12. 39 if block B has an upward speed of 2 m/s. Determine the displacement of the block at B if A is pulled down 1 m?