Dynamical Systems 2 Topological classification Ing Jaroslav Jra

Dynamical Systems 2 Topological classification Ing. Jaroslav Jíra, CSc.

More Basic Terms Basin of attraction is the region in state space of all initial conditions that tend to a particular solution such as a limit cycle, fixed point, or other attractor. Trajectory is a solution of equation of motion, it is a curve in phase space parametrized by the time variable. Flow of a dynamical system is the expression of its trajectory or beam of its trajectories in the phase space, i. e. the movement of the variable(s) in time Nullclines are the lines where the time derivative of one component of the state variable is zero. Separatrix is a boundary separating two modes of behavior of the dynamical system. In 2 D cases it is a curve separating two neighboring basins of attraction.

A Simple Pendulum Differential equation After transformation into two first order equations

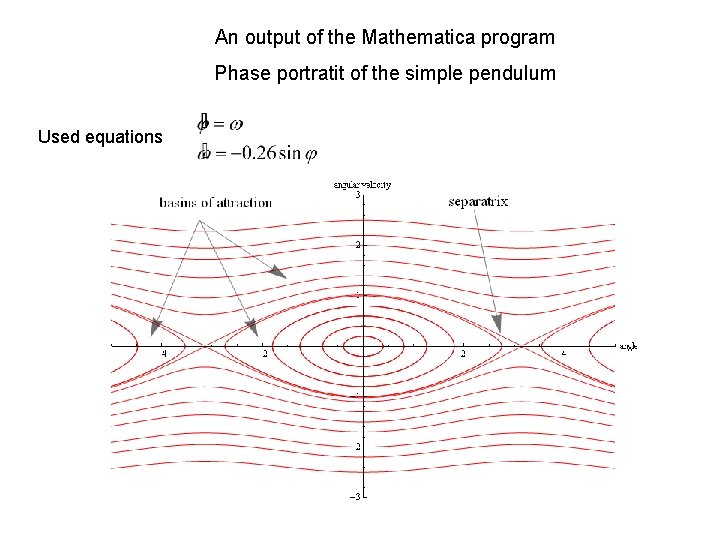
An output of the Mathematica program Phase portratit of the simple pendulum Used equations

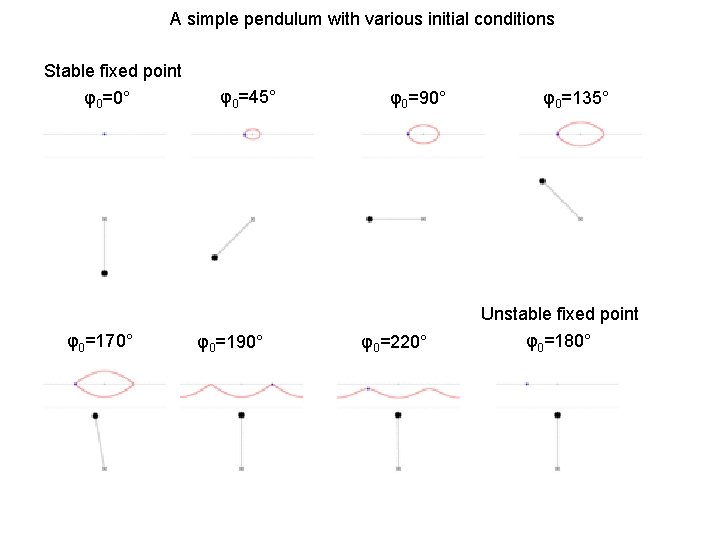
A simple pendulum with various initial conditions Stable fixed point φ0=0° φ0=45° φ0=90° φ0=135° Unstable fixed point φ0=170° φ0=190° φ0=220° φ0=180°

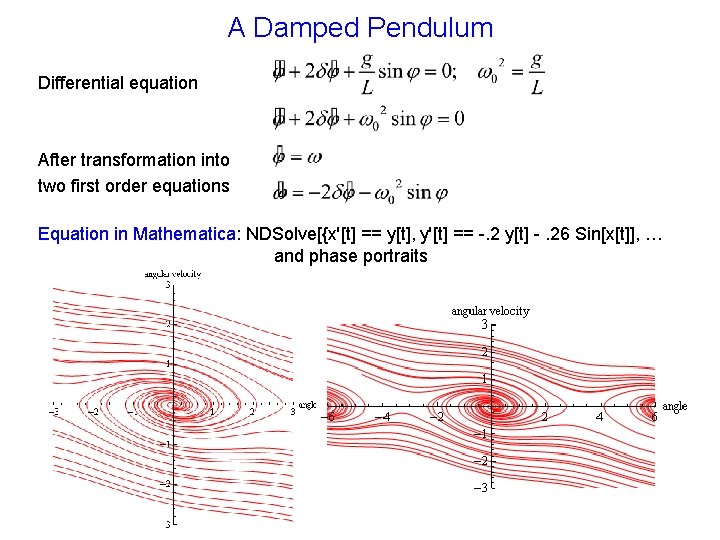
A Damped Pendulum Differential equation After transformation into two first order equations Equation in Mathematica: NDSolve[{x'[t] == y[t], y'[t] == -. 2 y[t] -. 26 Sin[x[t]], … and phase portraits

A Damped Pendulum commented phase portrait Nullcline determination: At the crossing points of the null clines we can find fixed points.

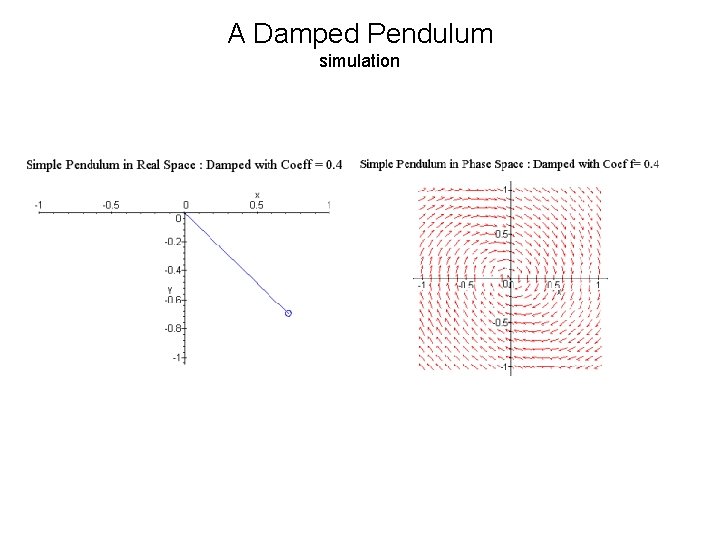
A Damped Pendulum simulation

Classification of Dynamical Systems One-dimensional linear or linearized systems Time Continous Discrete Derivative at x~ Fixed point is f’(x~)<0 Stable f’(x~)>0 Unstable f’(x~)=0 Cannot decide |f’(x~)|<1 Stable |f’(x~)|>1 Unstable |f’(x~)|=1 Cannot decide

Verification from the bacteria example Bacteria equation Derivative 1 st fixed point - unstable 2 nd fixed point - stable

Classification of Dynamical Systems Two-dimensional linear or linearized systems Set of equations for 2 D system Jacobian matrix for 2 D system Calculation of eigenvalues Formulation using trace and determinant

Types of two-dimensional linear systems 1. Attracting Node (Sink) Equations Jacobian matrix Eigenvalues Eigenvectors λ 1= -1 λ 2= -4 Solution from Mathematica Conclusion: there is a stable fixed point, the attracting node (sink)

A quick preview by the Vectorplot function in the Mathematica

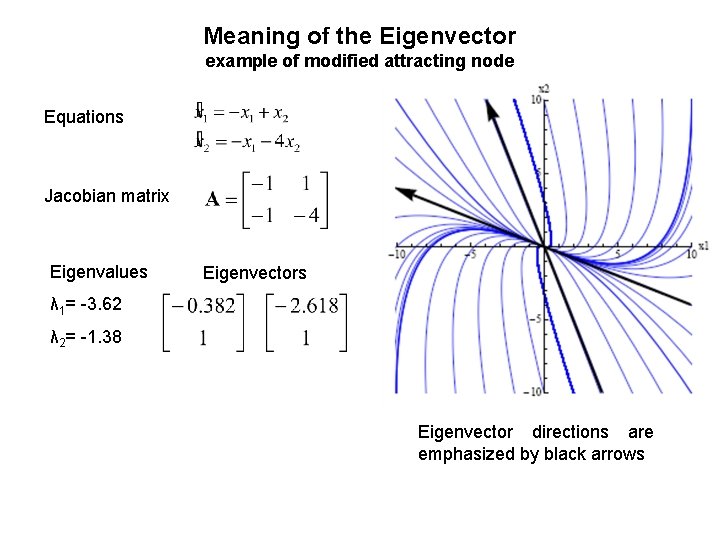
Meaning of the Eigenvector example of modified attracting node Equations Jacobian matrix Eigenvalues Eigenvectors λ 1= -3. 62 λ 2= -1. 38 Eigenvector directions are emphasized by black arrows

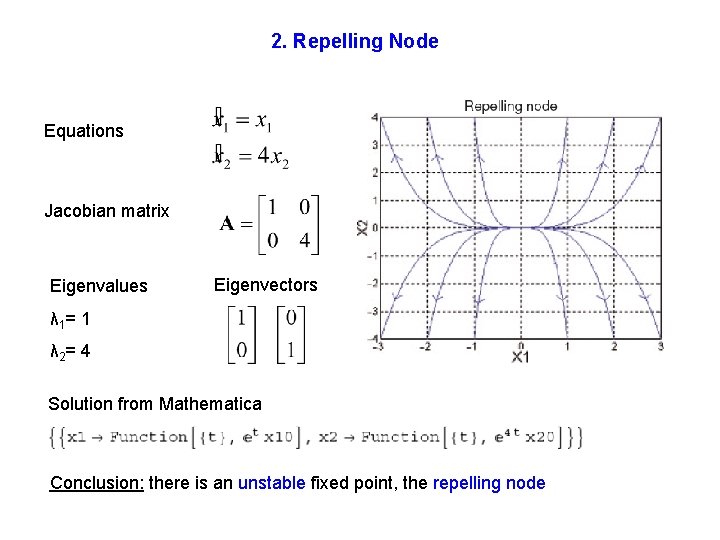
2. Repelling Node Equations Jacobian matrix Eigenvalues Eigenvectors λ 1= 1 λ 2= 4 Solution from Mathematica Conclusion: there is an unstable fixed point, the repelling node

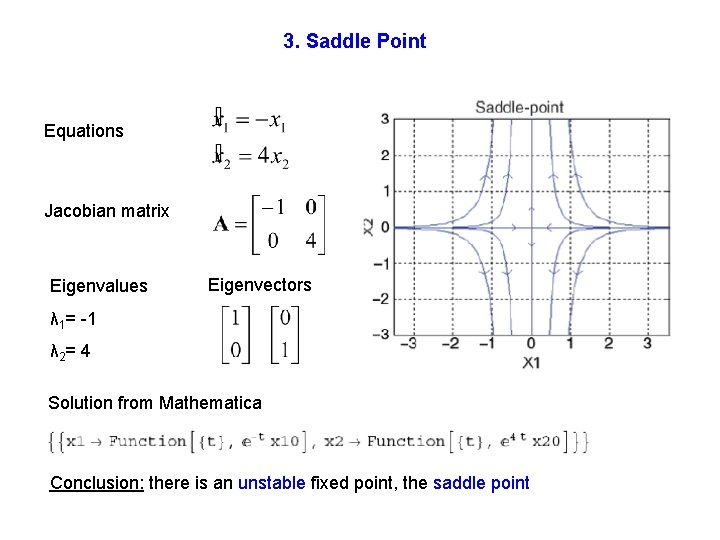
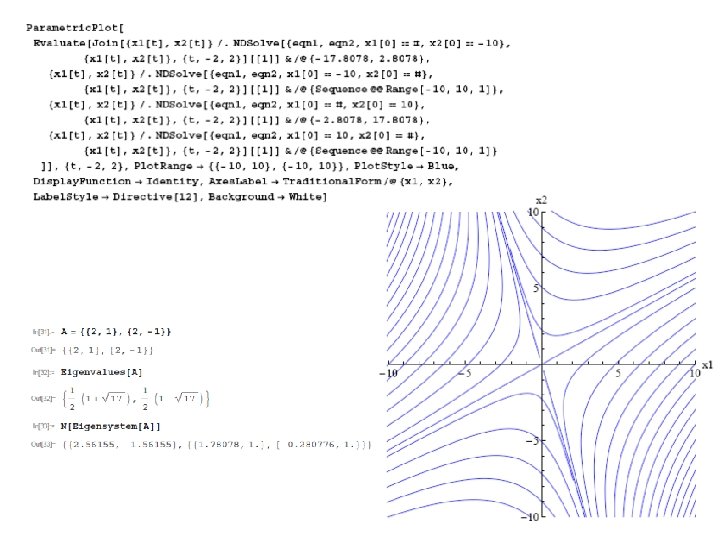
3. Saddle Point Equations Jacobian matrix Eigenvalues Eigenvectors λ 1= -1 λ 2= 4 Solution from Mathematica Conclusion: there is an unstable fixed point, the saddle point

4. Spiral Source (Repelling Spiral) Equations Jacobian matrix Eigenvalues Eigenvectors λ 1= 1+2 i λ 2= 1 -2 i Solution from Mathematica Conclusion: there is an unstable fixed point, the spiral source sometimes called unstable focal point

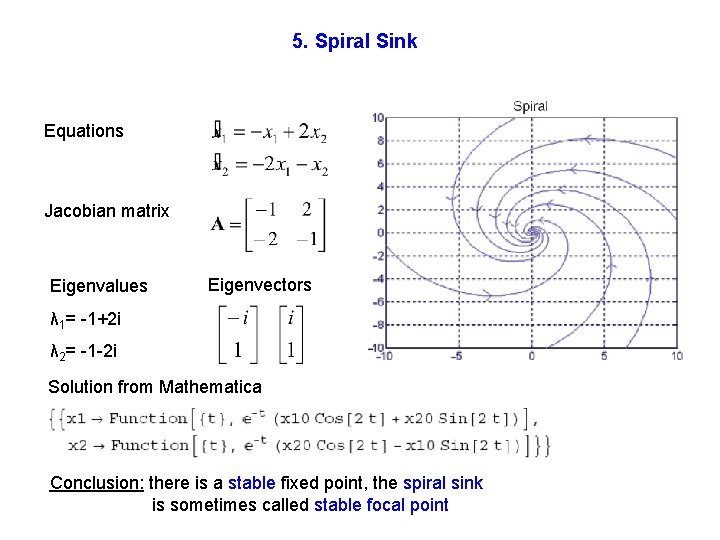
5. Spiral Sink Equations Jacobian matrix Eigenvalues Eigenvectors λ 1= -1+2 i λ 2= -1 -2 i Solution from Mathematica Conclusion: there is a stable fixed point, the spiral sink is sometimes called stable focal point

6. Node Center Equations Jacobian matrix Eigenvalues Eigenvectors λ 1= +1. 732 i λ 2= -1. 732 i Solution from Mathematica Conclusion: there is marginally stable (neutral) fixed point, the node center

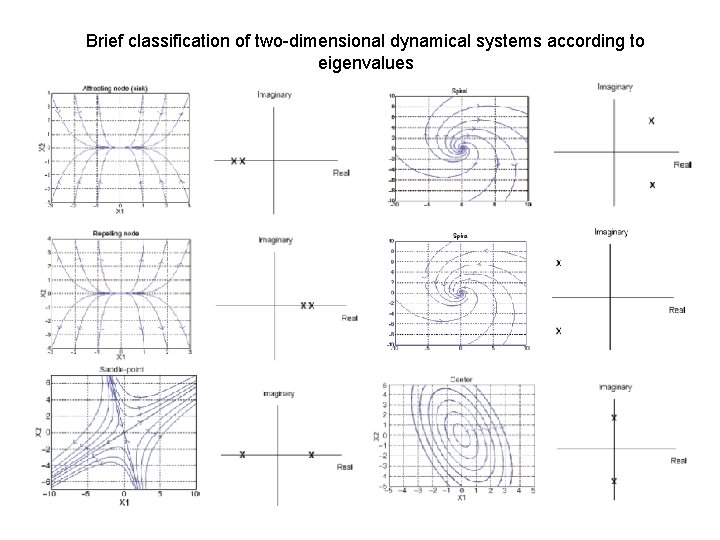
Brief classification of two-dimensional dynamical systems according to eigenvalues

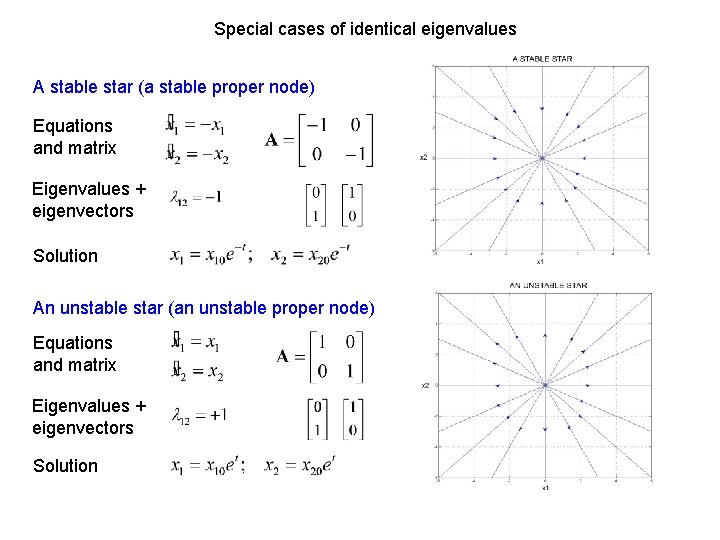
Special cases of identical eigenvalues A stable star (a stable proper node) Equations and matrix Eigenvalues + eigenvectors Solution An unstable star (an unstable proper node) Equations and matrix Eigenvalues + eigenvectors Solution

Special cases of identical eigenvalues A stable improper node with 1 eigenvector Equations and matrix Eigenvalues + eigenvectors Solution An unstable improper node with 1 eigenvector Equations and matrix Eigenvalues + eigenvectors Solution

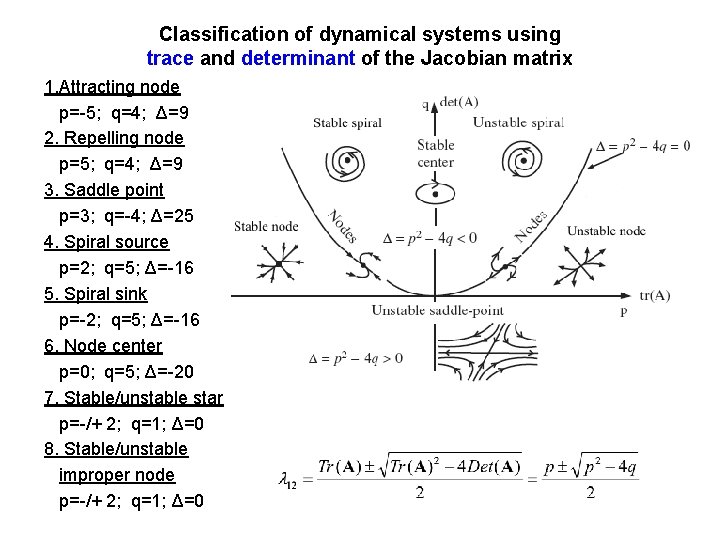
Classification of dynamical systems using trace and determinant of the Jacobian matrix 1. Attracting node p=-5; q=4; Δ=9 2. Repelling node p=5; q=4; Δ=9 3. Saddle point p=3; q=-4; Δ=25 4. Spiral source p=2; q=5; Δ=-16 5. Spiral sink p=-2; q=5; Δ=-16 6. Node center p=0; q=5; Δ=-20 7. Stable/unstable star p=-/+ 2; q=1; Δ=0 8. Stable/unstable improper node p=-/+ 2; q=1; Δ=0

Several configurations of damped oscillator Equation of motion Rewritten into a set of 1 st order equations Overdamped oscillator, δ=2 s-1, ω=1 s-1 Attracting node Underdamped oscillator, δ=1 s-1, ω=2 s-1 Spiral sink Critically damped osc. , δ=1 s-1, ω=1 s-1 Stable improper node Simple harmonic osc. , δ=0 s-1, ω=1 s-1 Node center

Example 1 – a saddle point calculation in Mathematica

Classification of Dynamical Systems Linear or linearized systems with more dimensions Time Eigenvalues all Re(λ)<0 Continous Stable some Re(λ)>0 Unstable all Re(λ)<=0 some Re(λ)=0 Cannot decide all |λ|<1 Discrete Fixed point is Stable some |λ|>1 Unstable all |λ|<=1 some |λ|=1 Cannot decide

Basic Types of 3 D systems Node – all eigenvalues are real and have the same sign Attracting Node – all eigenvalues are negative Repelling Node – all eigenvalues are positive λ 1< λ 2< λ 3< 0 λ 1> λ 2> λ 3> 0

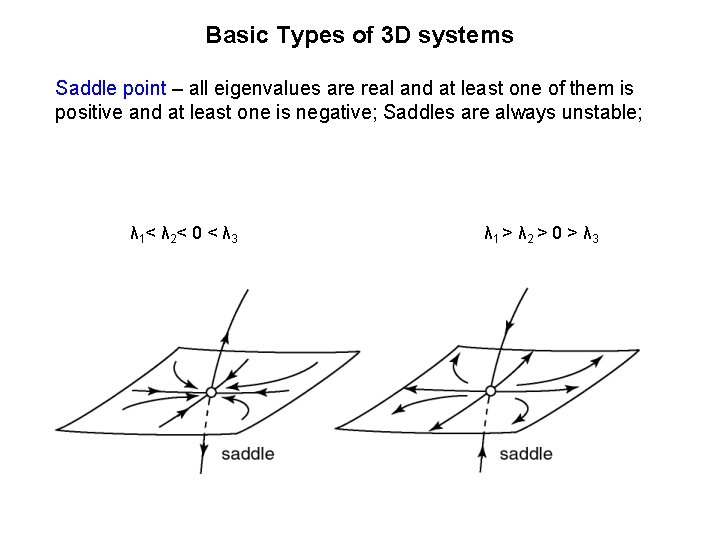
Basic Types of 3 D systems Saddle point – all eigenvalues are real and at least one of them is positive and at least one is negative; Saddles are always unstable; λ 1< λ 2< 0 < λ 3 λ 1 > λ 2 > 0 > λ 3

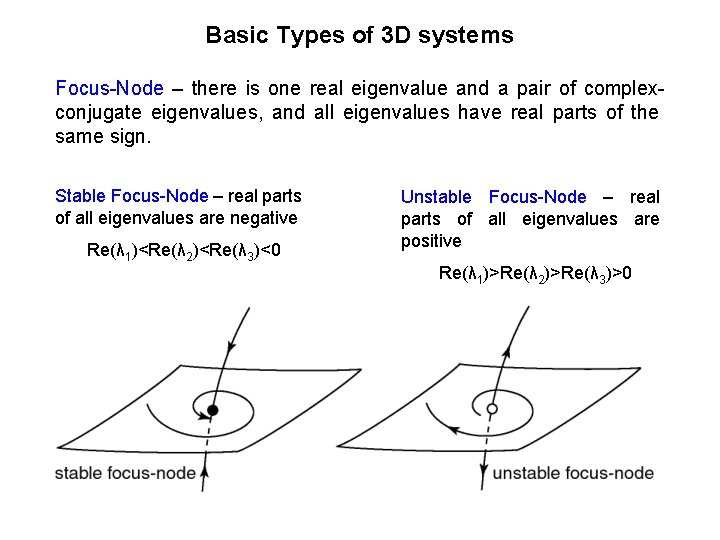
Basic Types of 3 D systems Focus-Node – there is one real eigenvalue and a pair of complexconjugate eigenvalues, and all eigenvalues have real parts of the same sign. Stable Focus-Node – real parts of all eigenvalues are negative Re(λ 1)<Re(λ 2)<Re(λ 3)<0 Unstable Focus-Node – real parts of all eigenvalues are positive Re(λ 1)>Re(λ 2)>Re(λ 3)>0

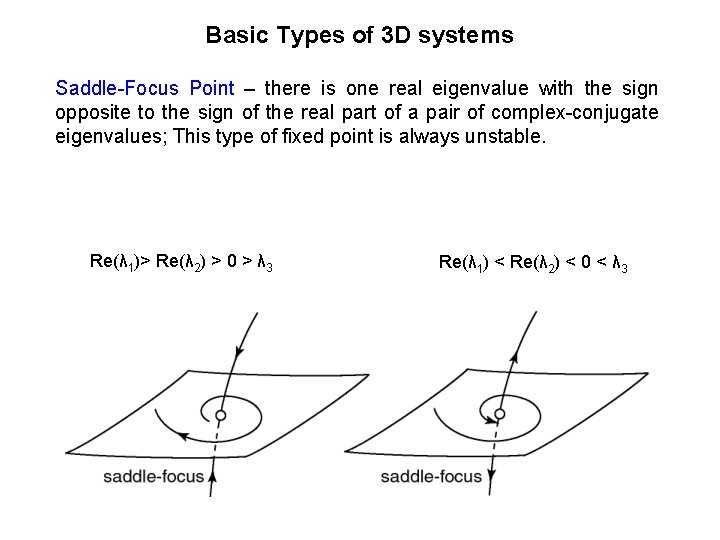
Basic Types of 3 D systems Saddle-Focus Point – there is one real eigenvalue with the sign opposite to the sign of the real part of a pair of complex-conjugate eigenvalues; This type of fixed point is always unstable. Re(λ 1)> Re(λ 2) > 0 > λ 3 Re(λ 1) < Re(λ 2) < 0 < λ 3